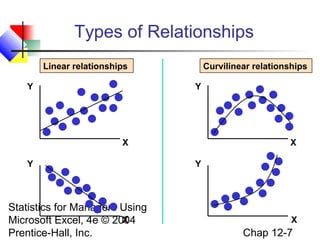
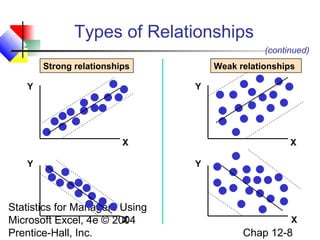
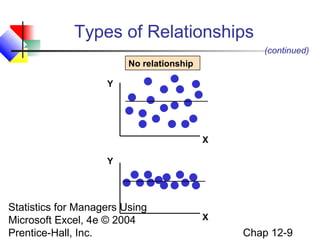
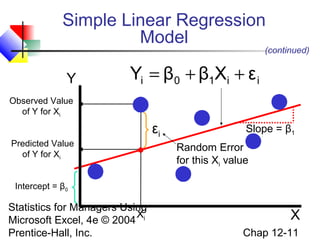
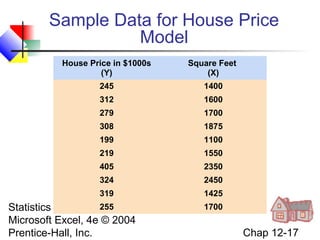
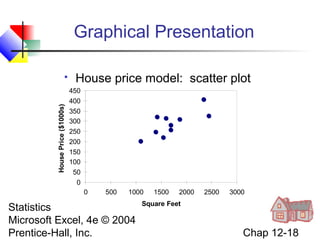
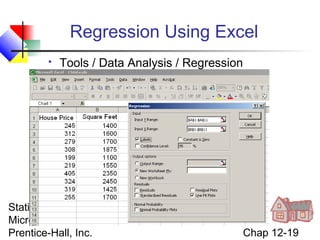
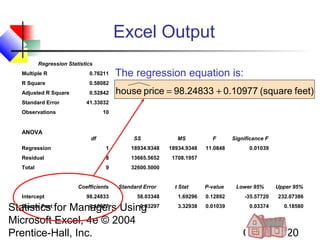
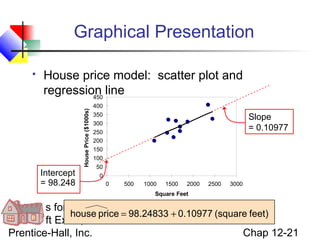
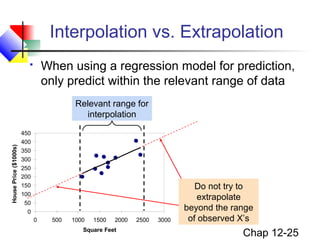
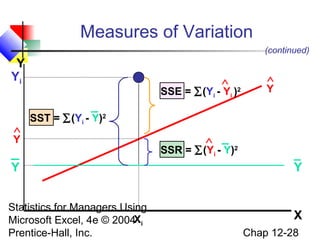
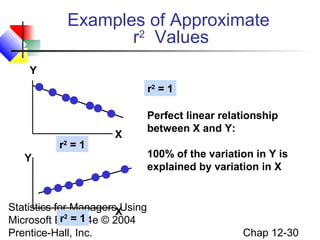
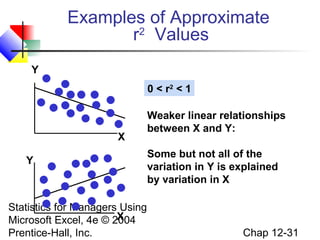
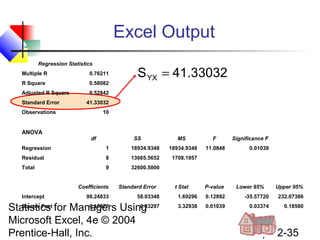
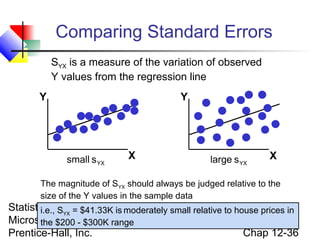
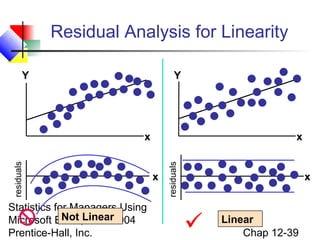
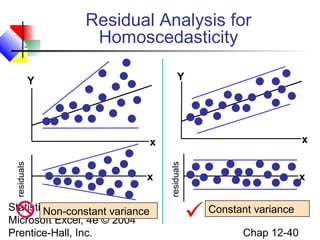
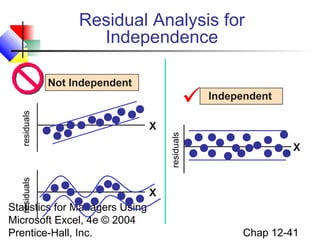
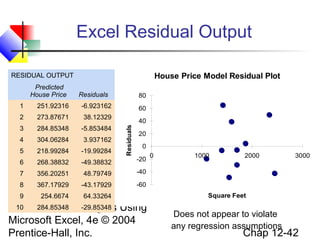
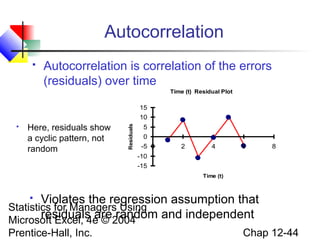
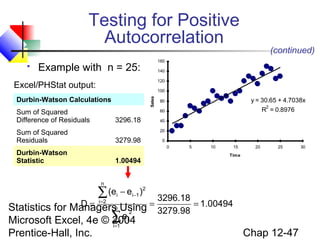
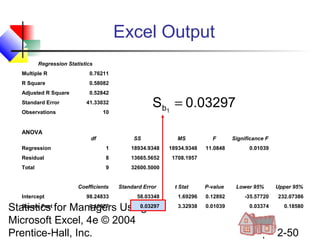
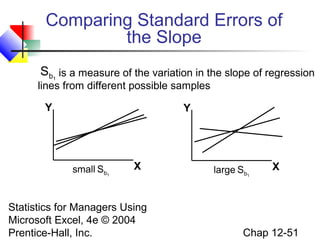
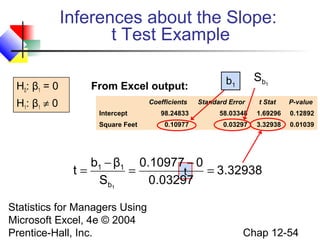
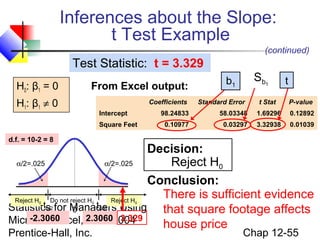
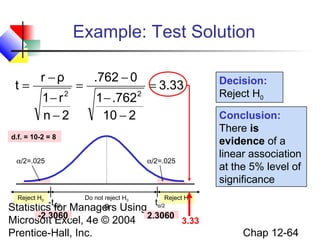
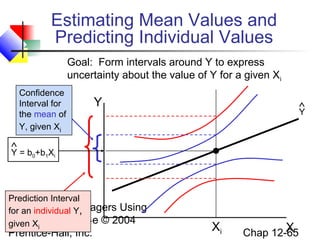
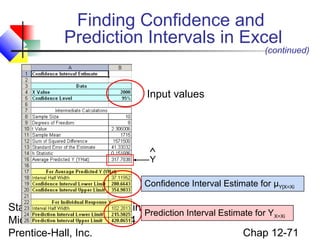
This chapter discusses simple linear regression analysis. It explains that regression analysis is used to predict the value of a dependent variable based on the value of at least one independent variable. The chapter outlines the simple linear regression model, which involves one independent variable and attempts to describe the relationship between the dependent and independent variables using a linear function. It provides examples to demonstrate how to obtain and interpret the regression equation and coefficients based on sample data. Key outputs from regression analysis like measures of variation, the coefficient of determination, and tests of significance are also introduced.