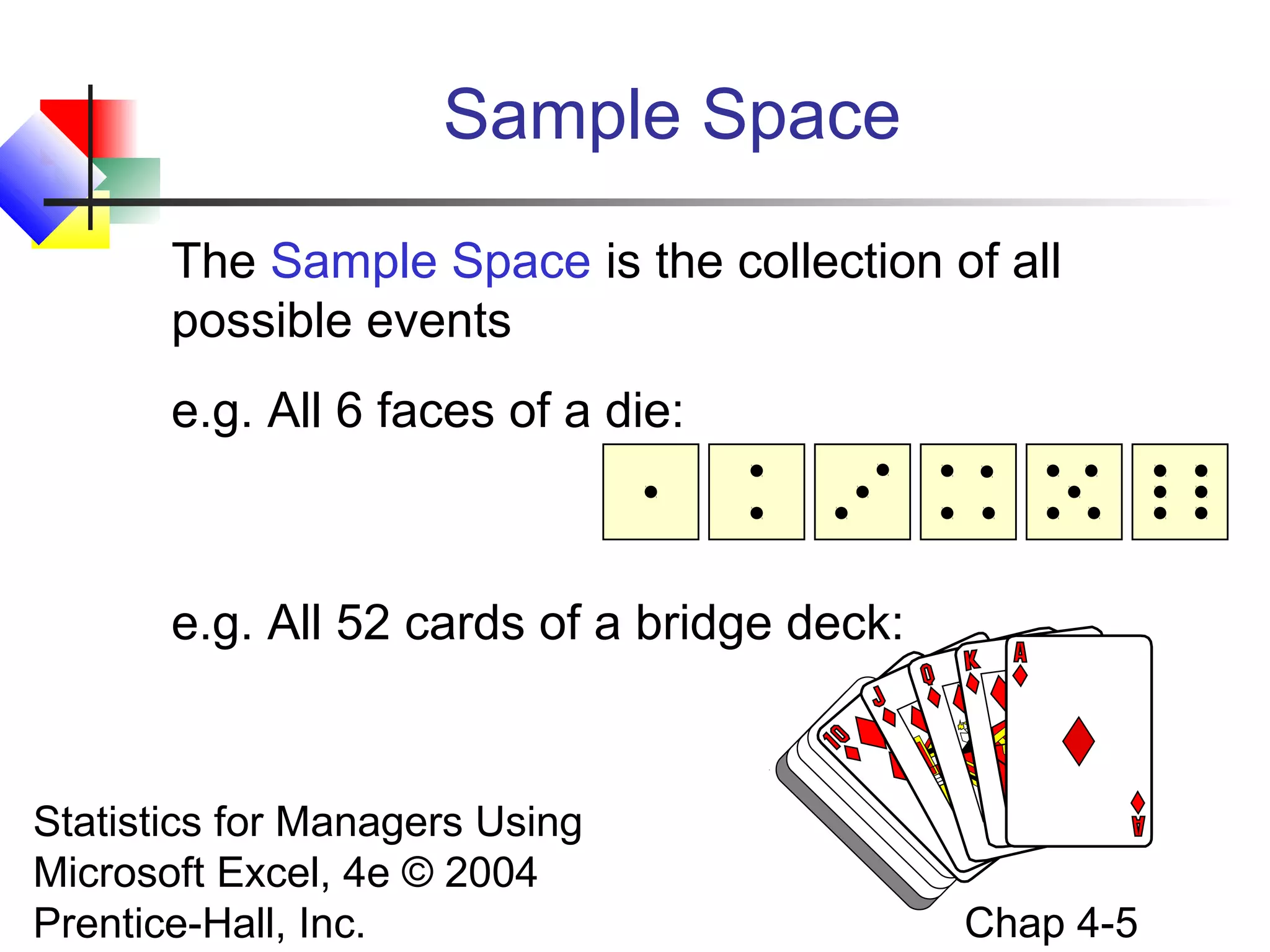
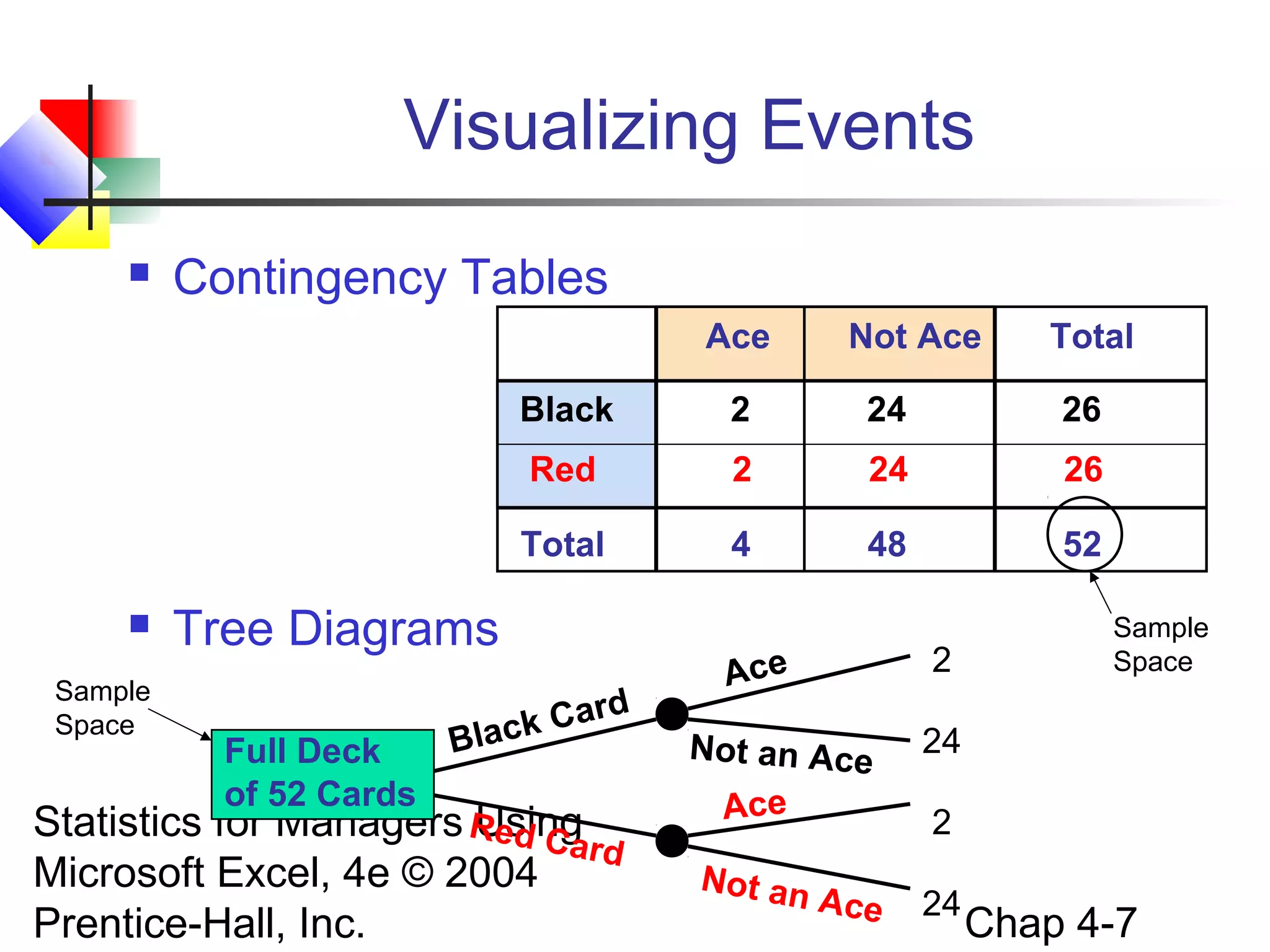
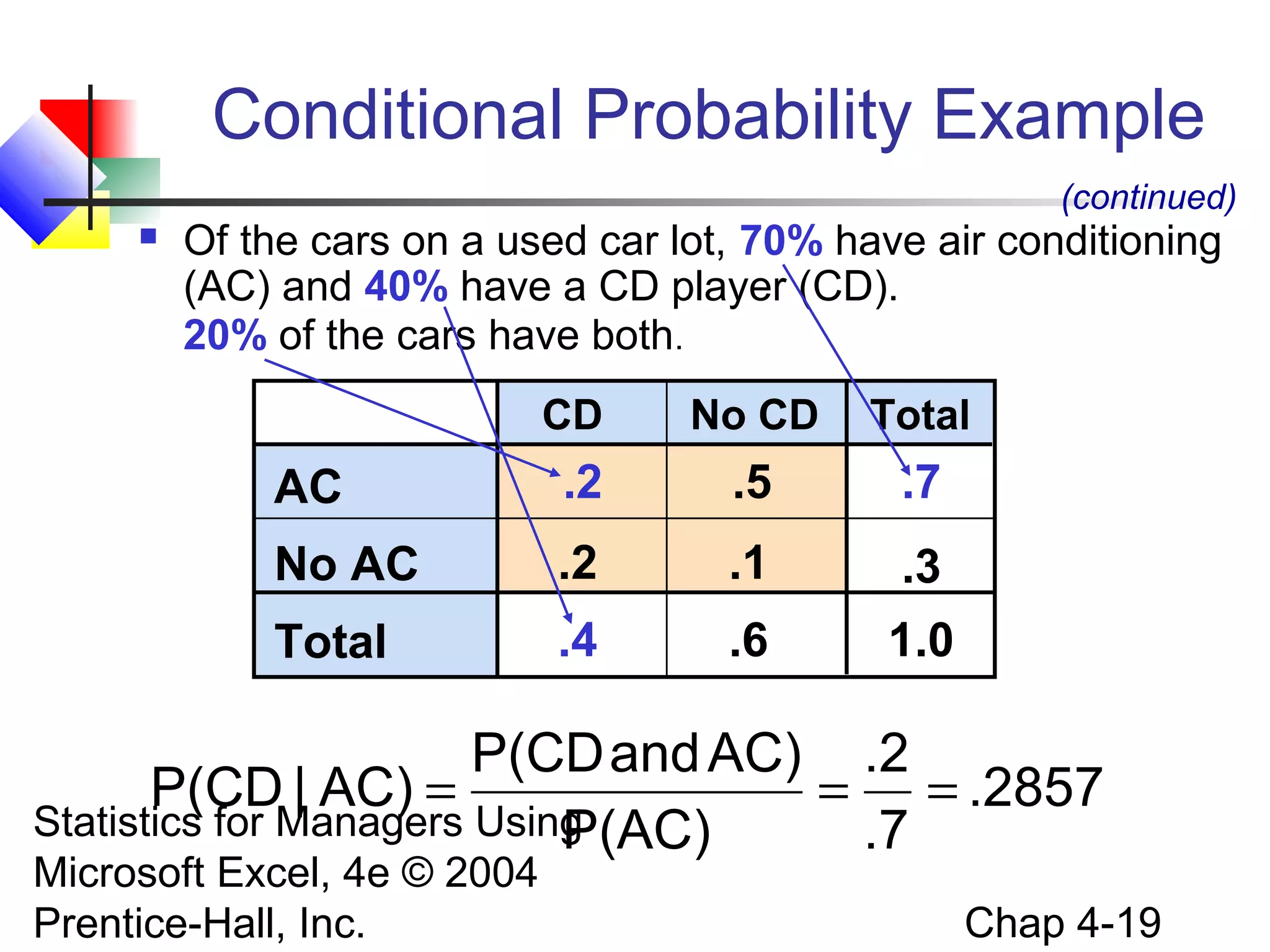
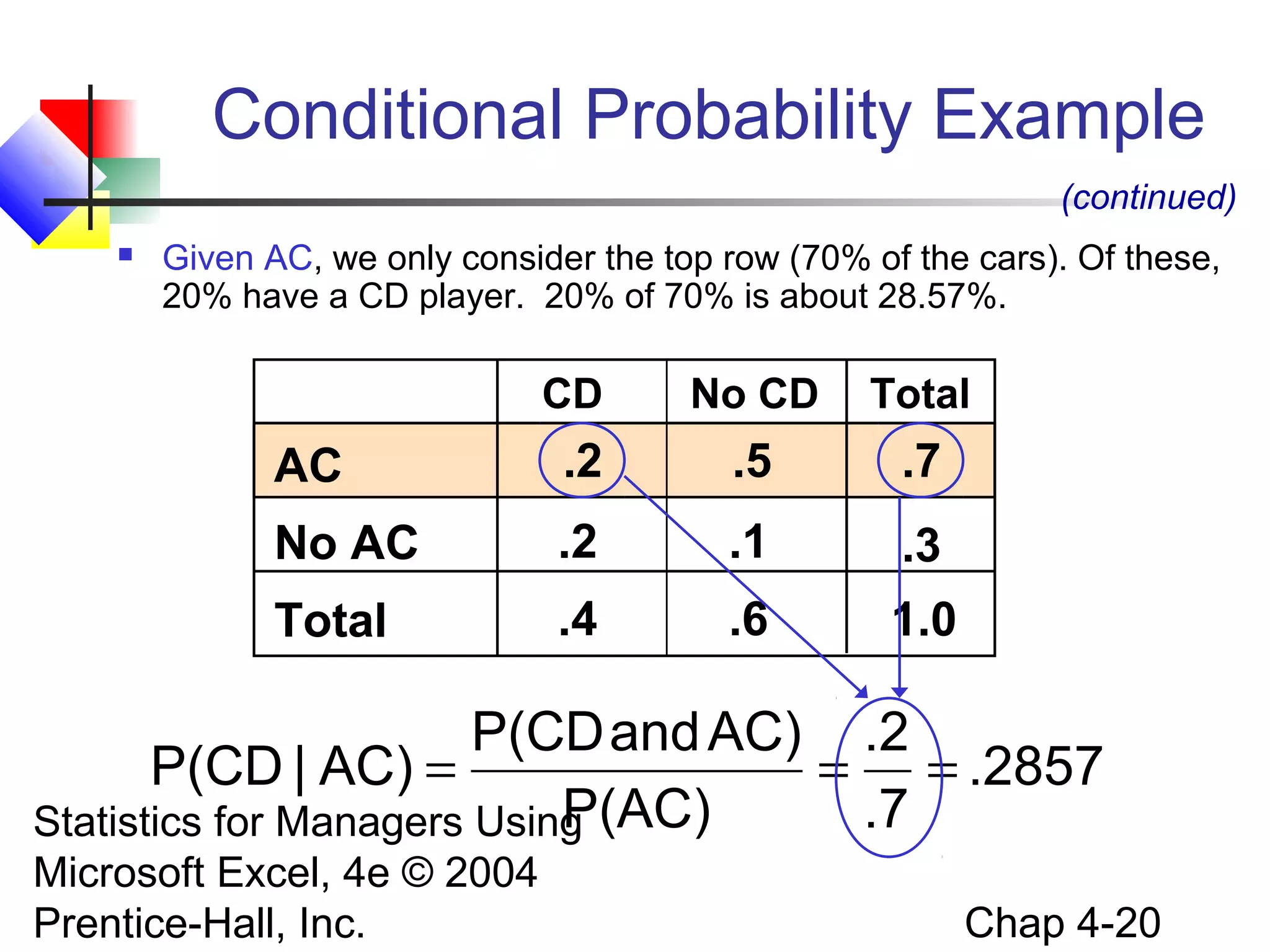
This chapter discusses basic probability concepts, including defining probability, sample spaces, simple and joint events, and assessing probability through classical and subjective approaches. It also covers key probability rules like the general addition rule, computing conditional probabilities, statistical independence, and Bayes' theorem. The goals are to explain these fundamental probability topics, show how to apply common probability rules, and determine if events are statistically independent or dependent.

1. Statistics for Managers
Using Microsoft® Excel
4th Edition
Chapter 4
Basic Probability
Statistics for Managers Using Microsoft Excel, 4e © 2004 Prentice-Hall, Inc.
Chap 4-1

2. Chapter Goals
After completing this chapter, you should be
able to:
 Explain basic probability concepts and definitions
 Use contingency tables to view a sample space
 Apply common rules of probability
 Compute conditional probabilities
 Determine whether events are statistically
independent
 Use Bayes’ Theorem
Statistics for Managers Using for conditional probabilities
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-2

3. Important Terms




Probability – the chance that an uncertain event
will occur (always between 0 and 1)
Event – Each possible type of occurrence or
outcome
Simple Event – an event that can be described
by a single characteristic
Sample Space – the collection of all possible
events
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-3

4. Assessing Probability

There are three approaches to assessing the probability
of un uncertain event:
1. a priori classical probability
probability of occurrence =
X
number of ways the event can occur
=
T
total number of elementary outcomes
2. empirical classical probability
probability of occurrence =
number of favorable outcomes observed
total number of outcomes observed
3. subjective probability
an individual Using
Statistics for Managers judgment or opinion about the probability of occurrence
Microsoft Excel, 4e © 2004
Chap 4-4
Prentice-Hall, Inc.

5. Sample Space
The Sample Space is the collection of all
possible events
e.g. All 6 faces of a die:
e.g. All 52 cards of a bridge deck:
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-5

6. Events

Simple event



Complement of an event A (denoted A’)



An outcome from a sample space with one
characteristic
e.g., A red card from a deck of cards
All outcomes that are not part of event A
e.g., All cards that are not diamonds
Joint event
Involves two or more characteristics simultaneously
Statisticsfor Managers that is also red from a deck of cards
e.g., An ace Using
Microsoft Excel, 4e © 2004
Chap 4-6
Prentice-Hall, Inc.


7. Visualizing Events

Contingency Tables
Ace
Not Ace
Total
Black
26
2
24
26
Total
Sample
Space
24
Red

2
4
48
52
Tree Diagrams
Full Deck
of 52 Cards
ar
ack C
Bl
d
Statistics for Managers Red Ca
Using
rd
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
2
Ac e
No t a n A c e
Ace
No t a n
Sample
Space
24
2
Ace
24
Chap 4-7

8. Mutually Exclusive Events

Mutually exclusive events

Events that cannot occur together
example:
A = queen of diamonds; B = queen of clubs

Events A and B are mutually exclusive
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-8

9. Collectively Exhaustive Events

Collectively exhaustive events


One of the events must occur
The set of events covers the entire sample space
example:
A = aces; B = black cards;
C = diamonds; D = hearts
Events A, B, C and D are collectively exhaustive
(but not mutually exclusive – an ace may also be
a heart)
 Events B, C
Statistics for Managersand D are collectively exhaustive and
Using
also mutually exclusive
Microsoft Excel, 4e © 2004
Chap 4-9
Prentice-Hall, Inc.


10. Probability


Probability is the numerical measure
of the likelihood that an event will
occur
The probability of any event must be
between 0 and 1, inclusively
0 ≤ P(A) ≤ 1 For any event A
The sum of the probabilities of all
mutually exclusive and collectively
exhaustive events is 1
P(A) + P(B) + P(C) = 1
Statistics for Managers Using
If A, B, and C are mutually exclusive and
Microsoft Excel, 4e © 2004
collectively exhaustive
Prentice-Hall, Inc.
1
Certain
.5

0
Impossible
Chap 4-10

11. Computing Joint and
Marginal Probabilities

The probability of a joint event, A and B:
number of outcomes satisfying A and B
P( A and B) =
total number of elementary outcomes

Computing a marginal (or simple) probability:
P(A) = P(A and B1 ) + P(A and B 2 ) +  + P(A and Bk )
Where B1, B …, Bk
Statistics for Managers2,Usingare k mutually exclusive and collectively
exhaustive events
Microsoft Excel, 4e © 2004
Chap 4-11
Prentice-Hall, Inc.


12. Joint Probability Example
P(Red and Ace)
=
number of cards that are red and ace 2
=
total number of cards
52
Type
Color
Red
Black
Total
Ace
2
2
4
Non-Ace
24
24
48
Statistics forTotal
Managers Using
26
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
26
52
Chap 4-12

13. Marginal Probability Example
P(Ace)
= P( Ace and Re d) + P( Ace and Black ) =
Type
Color
2
2
4
+
=
52 52 52
Red
Black
Total
Ace
2
2
4
Non-Ace
24
24
48
Statistics forTotal
Managers Using
26
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
26
52
Chap 4-13

14. Joint Probabilities Using
Contingency Table
Event
Event
B1
B2
Total
A1
P(A1 and B1) P(A1 and B2)
A2
P(A2 and B1) P(A2 and B2) P(A2)
Total
P(B1)
P(B2)
P(A1)
1
Joint for Managers Using Marginal (Simple) Probabilities
Statistics Probabilities
Microsoft Excel, 4e © 2004
Chap 4-14
Prentice-Hall, Inc.

15. General Addition Rule
General Addition Rule:
P(A or B) = P(A) + P(B) - P(A and B)
If A and B are mutually exclusive, then
P(A and B) = 0, so the rule can be simplified:
P(A or B) = P(A) + P(B)
For mutually exclusive events A and B
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Chap 4-15
Prentice-Hall, Inc.

16. General Addition Rule Example
P(Red or Ace) = P(Red) +P(Ace) - P(Red and Ace)
= 26/52 + 4/52 - 2/52 = 28/52
Type
Color
Red
Black
Total
Ace
2
2
4
Non-Ace
24
24
48
Total
26
26
Don’t count
the two red
aces twice!
52
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-16

17. Computing Conditional
Probabilities

A conditional probability is the probability of one
event, given that another event has occurred:
P(A and B)
P(A | B) =
P(B)
The conditional
probability of A given
that B has occurred
P(A and B)
P(B | A) =
P(A)
The conditional
probability of B given
that A has occurred
Where P(A and B) = joint probability of A and B
P(A) = marginal
Statistics for Managers Using probability of A
P(B) = marginal probability of B
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-17

18. Conditional Probability Example


Of the cars on a used car lot, 70% have air
conditioning (AC) and 40% have a CD player
(CD). 20% of the cars have both.
What is the probability that a car has a CD
player, given that it has AC ?
i.e., we want to find P(CD | AC)
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-18

19. Conditional Probability Example
(continued)

Of the cars on a used car lot, 70% have air conditioning
(AC) and 40% have a CD player (CD).
20% of the cars have both.
CD
No CD
Total
AC
.2
.5
.7
No AC
.2
.1
.3
Total
.4
.6
1.0
P(CD and AC) .2
P(CD | AC) =
= = .2857
Statistics for Managers Using
P(AC)
.7
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-19

20. Conditional Probability Example
(continued)

Given AC, we only consider the top row (70% of the cars). Of these,
20% have a CD player. 20% of 70% is about 28.57%.
CD
No CD
Total
AC
.2
.5
.7
No AC
.2
.1
.3
Total
.4
.6
1.0
P(CD and AC) .2
P(CD | AC) =
= = .2857
P(AC)
.7
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-20

21. Using Decision Trees
.2
D .7
C
Has
Given AC or
no AC:
P(A
H
All
Cars
)= .
C
7
C
sA
a
Do
e
hav s not
eA
P(A
C
C’)
= .3
P(AC and CD) = .2
D oe
s no
t .5
have
CD
P(AC and CD’) = .5
.7
.2
D .3
C
Has
D
P(AC’ and CD) = .2
Statistics for Managers Usingh oes not
ave
CD .1 P(AC’ and CD’) = .1
Microsoft Excel, 4e © 2004
.3
Chap 4-21
Prentice-Hall, Inc.

22. Using Decision Trees
C
as A
H
Given CD or
no CD:
P(C
H
All
Cars
C
as
)= .
D
4
D
Do
e
hav s not
eC
D P(C
D’)
= .6
.2
.4
D oe
s no
t .2
have
AC
(continued)
P(CD and AC) = .2
P(CD and AC’) = .2
.4
.5
.6
C
A
Has
D
P(CD’ and AC) = .5
Statistics for Managers Usingh oes not
ave
AC .1 P(CD’ and AC’) = .1
Microsoft Excel, 4e © 2004
.6
Chap 4-22
Prentice-Hall, Inc.

23. Statistical Independence

Two events are independent if and only
if:
P(A | B) = P(A)

Events A and B are independent when the probability
of one event is not affected by the other event
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-23

24. Multiplication Rules

Multiplication rule for two events A and B:
P(A and B) = P(A | B) P(B)
Note: If A and B are independent, then P(A | B) = P(A)
and the multiplication rule simplifies to
P(A and B) = P(A) P(B)
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-24

25. Marginal Probability

Marginal probability for event A:
P(A) = P(A | B1 ) P(B1 ) + P(A | B 2 ) P(B 2 ) +  + P(A | Bk ) P(Bk )

Where B1, B2, …, Bk are k mutually exclusive and
collectively exhaustive events
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-25

26. Bayes’ Theorem
P(A | Bi )P(Bi )
P(Bi | A) =
P(A | B1 )P(B1 ) + P(A | B 2 )P(B 2 ) +  + P(A | Bk )P(Bk )

where:
Bi = ith event of k mutually exclusive and collectively
exhaustive events
A = new event that might impact P(Bi)
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-26

27. Bayes’ Theorem Example

A drilling company has estimated a 40%
chance of striking oil for their new well.

A detailed test has been scheduled for more
information. Historically, 60% of successful
wells have had detailed tests, and 20% of
unsuccessful wells have had detailed tests.
Given that this well has been scheduled for a
detailed test, what is the probability
that the well will be
Statistics for Managers Usingsuccessful?

Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-27

28. Bayes’ Theorem Example
(continued)

Let S = successful well
U = unsuccessful well

P(S) = .4 , P(U) = .6

Define the detailed test event as D

Conditional probabilities:
P(D|S) = .6
(prior probabilities)
P(D|U) = .2
 Goal is to find P(S|D)
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Chap 4-28

29. Bayes’ Theorem Example
(continued)
Apply Bayes’ Theorem:
P(D | S)P(S)
P(S | D) =
P(D | S)P(S) + P(D | U)P(U)
(.6)(.4)
=
(.6)(.4) + (.2)(.6)
.24
=
= .667
.24 + .12
So the Managers Using
Statistics forrevised probability of success, given that this well
has been scheduled
Microsoft Excel, 4e © 2004 for a detailed test, is .667
Chap 4-29
Prentice-Hall, Inc.

30. Bayes’ Theorem Example
(continued)

Given the detailed test, the revised probability
of a successful well has risen to .667 from the
original estimate of .4
Event
Prior
Prob.
Conditional
Prob.
Joint
Prob.
Revised
Prob.
S (successful)
.4
.6
.4*.6 = .24
.24/.36 = .667
U (unsuccessful)
.6
.2
.6*.2 = .12
.12/.36 = .333
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.
Sum = .36
Chap 4-30

31. Chapter Summary

Discussed basic probability concepts


Examined basic probability rules


Sample spaces and events, contingency tables, simple
probability, and joint probability
General addition rule, addition rule for mutually exclusive events,
rule for collectively exhaustive events
Defined conditional probability

Statistical independence, marginal probability, decision trees,
and the multiplication rule
Discussed Bayes’ theorem
Statistics for Managers Using
Microsoft Excel, 4e © 2004
Prentice-Hall, Inc.

Chap 4-31