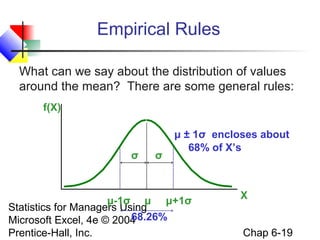
This document outlines the key goals and concepts covered in Chapter 6 of the textbook "Statistics for Managers Using Microsoft Excel". The chapter introduces continuous probability distributions, including the normal, uniform, and exponential distributions. It describes the characteristics of the normal distribution and how to translate problems into standardized normal distribution problems. The chapter also covers sampling distributions, the central limit theorem, and how to find probabilities using the normal distribution table.









![The Normal Probability
Density Function
The formula for the normal probability density
function is
f(X) =
Where
1
−(1/2)[(X −μ)/σ] 2
e
2πσ
e = the mathematical constant approximated by 2.71828
π = the mathematical constant approximated by 3.14159
μ = the population mean
Statistics forσManagers Using
= the population standard deviation
Microsoft Excel, 4e © 2004 continuous variable
X = any value of the
Prentice-Hall, Inc.
Chap 6-10](https://image.slidesharecdn.com/chap06normaldistributionscontinous-131031212033-phpapp02/85/Chap06-normal-distributions-continous-10-320.jpg)