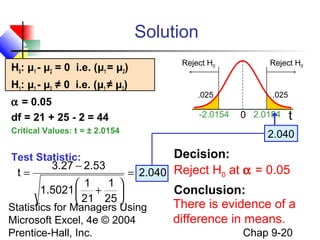
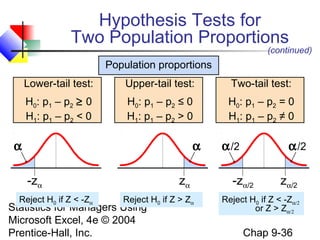
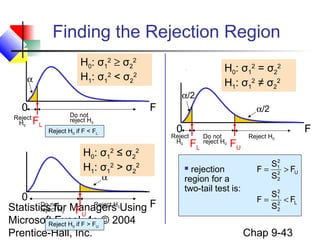
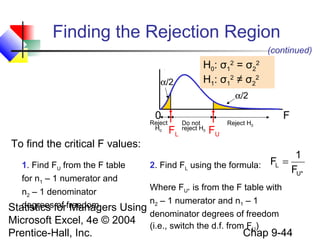
This chapter discusses methods for comparing two population means or proportions using statistical tests. It covers tests for independent samples, including the z-test when population variances are known and the t-test when they are unknown. It also addresses paired or related samples using a z-test when the population difference variance is known, and a t-test when it is unknown. Examples are provided for hypotheses tests and confidence intervals for the difference between two means or proportions.