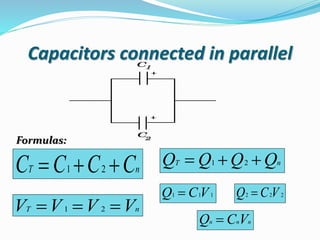
Group 1: BSME IV Gutierrez, Eduardo Jr. H. Cabanag, Cleo C. The document discusses capacitors, including their definition as a passive two-terminal electrical component used to temporarily store electrical energy in an electric field. It describes how capacitance is measured in Farads and depends on the physical properties of the capacitor such as plate area and separation. It also discusses how dielectrics can increase a capacitor's capacitance and the formulas used to calculate capacitance and energy storage for different capacitor configurations including parallel plate, spherical, and cylindrical capacitors.

1. Group 1: BSME IV
Gutierrez, Eduardo Jr. H.
Cabanag, Cleo C.

2. Capacitance
o Is the ability of a body to store an electrical charge. A material
with a large capacitance holds more electric charge at a given
voltage, than one with low capacitance. Any object that can be
electrically charged exhibits capacitance, however the concept is
particularly important for understanding the operations of the
capacitor, one of the three fundamental electronic components
(along with resistors and inductors).
o The SI unit of capacitance is the farad (symbol: F), named after
the English physicist Michael Faraday. A 1 farad capacitor, when
charged with 1 coulomb of electrical charge, has a potential
difference of 1 volt between its plates

3. Capacitor
Electronic symbol

4. o (originally known as a condenser) is a passive two-terminal
electrical component used to temporarily store electrical energy
in an electric field. The forms of practical capacitors vary widely,
but most contain at least two electrical conductors (plates)
separated by a dielectric.
o The conductors can be thin films, foils or sintered beads of
metal or conductive electrolyte, etc. Materials commonly used
as dielectrics include glass, ceramic, plastic film, paper, mica,
and oxide layers.
o Capacitors are widely used as parts of electrical circuits in many
common electrical devices. Unlike a resistor, an ideal capacitor
does not dissipate energy. Instead, a capacitor stores energy in
the form of an electrostatic field between its plates.

5. Applications of Capacitors
A microphone converts sound waves into an electrical signal
(varying voltage) by changing d.
+
++++++
-
-
-
-
-
- - A
Variable
Capacitor
Changing
Area
0
A
C
d

d
Changing d
Microphone
Q
V
C

The tuner in a radio is a variable capacitor. The changing area A alters
capacitance until desired signal is obtained.

6. Capacitance in Farads
One farad (F) is the capacitance C of a conductor that
holds one coulomb of charge for each volt of potential.
(C)
; (F)
(V)
Q coulomb
C farad
V volt
 
Example: When 40 μC of charge are placed on a
conductor, the potential is 8 V. What is the capacitance?
C = 5 μF
VV
Q
C
8
C40


7. Dielectric Materials
o Most capacitors have a dielectric
material between their plates to
provide greater dielectric strength
and less probability for electrical
discharge.
o The separation of dielectric
charge allows more charge to be
placed on the plates—greater
capacitance .
o Materials commonly used as
dielectrics include glass, ceramic,
plastic film, paper, mica, and
oxide layers.

8. o Smaller plate separation without contact.
o Increases capacitance of a capacitor.
o Higher voltages can be used without
breakdown.
o Often it allows for greater mechanical
strength.
Advantages of Dielectrics

9. Insertion of Dielectric
+
+
+
+
+
+
Co Vo Eo o
+Q
-Q
++
+Q
-Q
Permittivity increases.
 > o
Capacitance increases.
C > Co
Voltage decreases.
V < Vo
Field decreases.
E < Eo
Insertion of
a dielectric
Same Q
Q = Qo
C V E 

10. Dielectric Constant, εr
The dielectric constant εr for a material is the ratio of the
capacitance C with this material as compared with the
capacitance Co in a vacuum.
Dielectric constant:
εr= 1 for Air
εr can also be given in terms of voltage V, electric field
intensity E, or permittivity e:
0C
C
r 
0
00


 
E
E
V
V
r

11. The Permittivity of a Medium
The capacitance of a parallel plate capacitor with a dielectric
can be found from:
The constant ε is the permittivity of the medium which
relates to the density of field lines.
0CC r
d
A
C r 0
d
A
C or or
mFx.; εεεε r
112
1085800





12. Parallel Plate Capacitance
d
Area
A
+
Q
-Q
0
Q A
C
V d
 
Where:
C=Capacitance (F)
Q=Charge (C)
V=Voltage (V)
A=Area of the plate (m^2)
d=Plate separation (m)
ε0=Permittivity (8.85x10^-12 F/m)

13. Where:
C=Capacitance (F)
Q=Charge (C)
V=Voltage (V)
A=Area of the plate (m^2)
d=Plate separation (m)
ε0=Permittivity (8.85x10^-12 F/m)
εr=Dielectric constant
 321
0
rrr
nd
A
C 


If capacitor have two or more
dielectric:

14. Example : Find the capacitance C and the charge Q if connected to
200-V battery. Assume the dielectric constant is εr = 5.0.
2 mmd
A
0.5 m2
  εr 0
  εr 0 5(8.85 x 10-12F/m)
  44.25 x 10-12 F/m
C = 11.1 nF
Q if connected to V = 200 V?
Q = CV = (11.1 nF)(200 V) Q = 2.22 C
m
m
m
F
x
d
A
C
002.0
)5.0)(1025.44( 212
 

15. Spherical Capacitor








21
0
11
4
rr
V
Q
C

r1
r1
Where:
C=Capacitance
Q=Charge
V=Voltage
r1=Inside radius
r2=Outside radius r1
ε0=Permittivity (8.85x10^-12 F/m)

16. If spherical capacitor have two dielectrics:
r2
r3
r1
   23111232
3212104
rrrrrr
rrr
C
rr
rr




εr2
εr1

17. Cylindrical Capacitor
r1
r2
For a cylindrical geometry like a coaxial
cable, the capacitance is usually stated as a
capacitance per unit length. The charge
resides on the outer surface of the inner
conductor and the inner wall of the outer
conductor. The capacitance expression is







2
1
0
ln
2
r
rL
C r
Where:
C=Capacitance
Q=Charge
V=Voltage
r1=Inside radius
r2=Outside radius r1
L =Length of capacitor

18. If cylindrical capacitor have two dielectrics:
r2
r3
r1
εr2
εr1

























3
2
1
2
1
2
21
0
lnln
2
r
r
r
r
LC
rr
rr




19. Example: A cylindrical capacitor of length 8cm is made
of two concentric rings having an inner radius as 3cm
and outer radius as 6cm. Calculate the capacitance of
the capacitor.
Given:
L=8cm=0.08m
r1=3cm=0.03m
r2=6cm=0.06m
1
2
0
ln
2
r
r
LC
r









m
m
m
Fx
mC
03.0
06.0
ln
)1085.8)(1)(2(
)08.0(
12

FxC 12
1042.6 


20. Capacitors connected in series
Formulas:
nT QQQQ  21
nT VVVV  21
1
1
1
C
Q
V 
2
2
2
C
Q
V 
n
n
n
C
Q
V 
n
T
CCC
C
111
1
21



21. Capacitors connected in parallel
Formulas:
nT CCCC  21
nT QQQQ  21
nT VVVV  21
111 VCQ  222 VCQ 
nnn VCQ 

22. Example: C1=10F and C2=5F. Determine the effective
capacitance for C1 and C2 connected in series and in
parallel .
In Series:
21
111
CCCT

5
1
10
1
1

TC
FCT 3.3
In parallel
21 CCCT 
510 TC
FCT 15

23. Capacitors connected in
series-parallel
C2=4
C4=4C3=4
C1=4
Vt
Sol’n
21
12
11
1
CC
C


4
1
4
1
1
12

C
212 C

24. 43
34
11
1
CC
C


4
1
4
1
1
34

C
234 C
3412 CCCt  22 tC
4tC

25. Capacitors connected in
series-parallel
C2=4
C4=4C3=4
C1=4
Vt
Sol’n
3113 CCC 
4413 C
813 C

26. 4324 CCC  4424 C
824 C
2413
11
1
CC
Ct


8
1
8
1
1

tC
4tC

27. Energy storage
The energy (measured in joules) stored in a capacitor is equal to the
work required to push the charges into the capacitor, i.e. to charge
it. Consider a capacitor of capacitance C, holding a charge +q on
one plate and −q on the other. Moving a small element of charge dq
from one plate to the other against the potential difference V = q/C
requires the work dW:
dq
C
q
dW 
where W is the work measured in
joules, q is the charge measured in
coulombs and C is the capacitance,
measured in farads.

28. The energy stored in a capacitor is found by integrating this
equation. Starting with an uncharged capacitance (q = 0) and
moving charge from one plate to the other until the plates have
charge +Q and −Q requires the work W:
stored
2
2
0 2
1
2
1
2
1
charging WCVQV
C
Q
dq
C
q
W
Q
 
C
Q
W
2
2
1
 QVW
2
1
 2
2
1
CVW 

29. Example: The capacitor of 1 mF has charged to 100V. What
energy is stored in the capacitor in Joules?
C
Q
W
2
2
1
 QVW
2
1

2
2
1
CVW 
2
)100)(1(
2
1
VFW 
JW 5000
CVQ 
)100)(1( VFQ 
CQ 100
)100)(100(
2
1
VCW 
F
C
W
1
)100(
2
1 2

JW 5000JW 5000