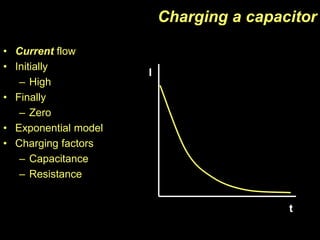
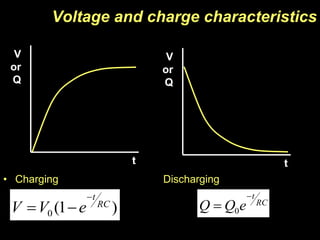
- A capacitor is an electronic component that stores charge and consists of two conducting surfaces separated by an insulating material. It is used for time delays, filtering, and tuned circuits. - Capacitors come in sandwich or Swiss roll constructions with metal plates separated by an insulating material. The capacitance is determined by the dielectric material and plate separation distance. - Capacitance is defined as the amount of charge stored per applied voltage. It is measured in Farads. The energy stored in a capacitor is equal to one-half the capacitance times the square of the applied voltage.

1. Capacitors

2. What is a capacitor?
• Electronic component
• Two conducting surfaces separated by an insulating material
• Stores charge
• Uses
– Time delays
– Filters
– Tuned circuits

3. Capacitor construction
• Two metal plates
• Separated by insulating
material
• ‘Sandwich’ construction
• ‘Swiss roll’ structure
• Capacitance set by...
d
A
C 

4. Defining capacitance
• ‘Good’ capacitors store a lot of charge…
• …when only a small voltage is applied
• Capacitance is charge stored per volt
• Capacitance is measured in farads F
– Big unit so nF, mF and F are used
V
Q
C 

5. Graphical representation
Equating to the equation of a straight line
mxy
CVQ
V
Q
C



Q
V
Gradient term is
the capacitance
of the capacitor
Charge stored is
directly
proportional to
the applied
voltage

6. Energy stored by a capacitor
• By general definition E=QV
– product of charge and voltage
• By graphical consideration...
QVE
2
1

Area term is
the energy
stored in the
capacitor
Q
V

7. Other expressions for energy
• By substitution of Q=CV
C
Q
E
CVE
QVE
2
2
2
1
2
1
2
1




8. Charging a capacitor
• Current flow
• Initially
– High
• Finally
– Zero
• Exponential model
• Charging factors
– Capacitance
– Resistance
I
t

9. Discharging a capacitor
• Current flow
• Initially
– High
– Opposite to charging
• Finally
– Zero
• Exponential model
• Discharging factors
– Capacitance
– Resistance
I
t

10. V
or
Q
t
V
or
Q
t
Voltage and charge characteristics
• Charging Discharging
RC
t
eQQ

 0)1(0
RC
t
eVV



11. • Product of
– Capacitance of the capacitor being charged
– Resistance of the charging circuit
– CR
• Symbol  ‘Tau’
• Unit seconds
Time constant
tCR
tQ
V
V
Q
CR




12. When t equals tau during discharge
• At t = tau the capacitor has
fallen to 37% of its original
value.
• By a similar analysis tau can
be considered to be the time
taken for the capacitor to
reach 63% of full charge.
37.00
1
0
0
0







QQ
eQQ
eQQ
eQQ
RC
RC
RC
t

13. Graphical determination of tau
• V at 37%
• Q at 37%
• Compared to initial
maximum discharge
V
or
Q
t
R
tC
RCt
t




14. Logarithmic discharge analysis
• Mathematical consideration of
discharge
• Exponential relationship
• Taking natural logs equates
expression to ‘y=mx+c’
• Gradient is -1/Tau
0
0
0
0
ln
1
ln
lnln
Vt
RC
V
RC
tVV
e
V
V
eVV
RC
t
RC
t









15. Logarithmic discharge graph
lnV
t
Gradient term
is the -1/Tau

16. Presented By…..
130170111092 Rathor Vijendrasingh
130170111095 Rudra Pavan
130170111098 Shah Nidhi
EC- J1  5th Semester, 2015
Thank You 