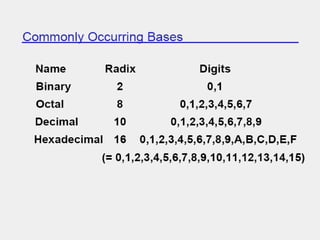
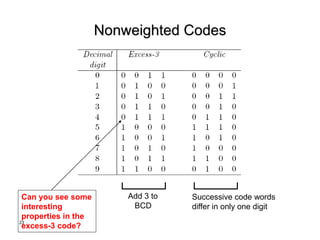
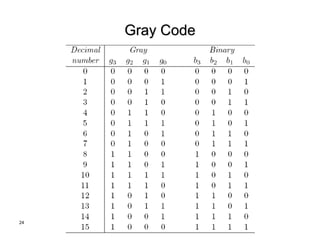
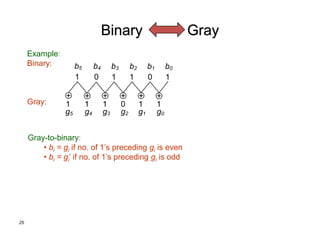
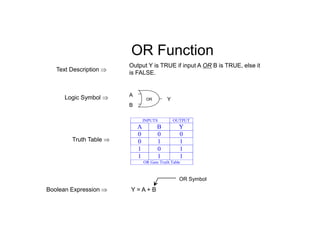
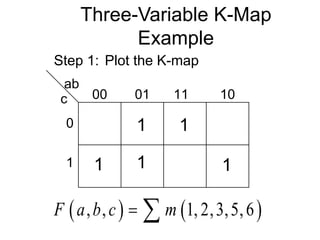
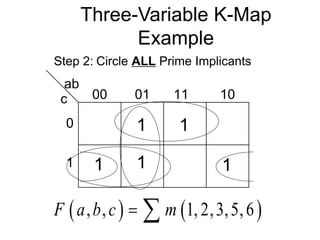
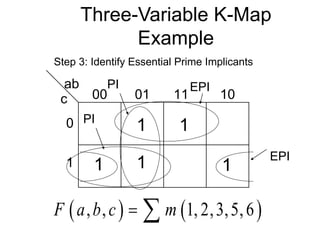
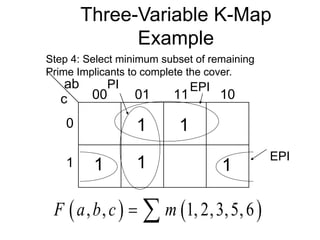
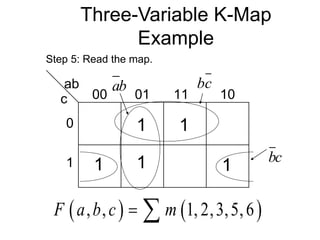
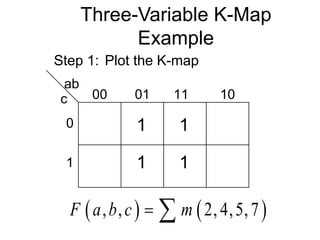
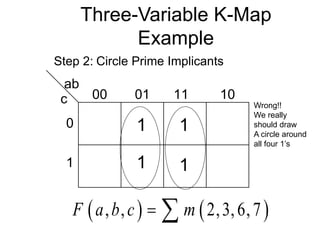
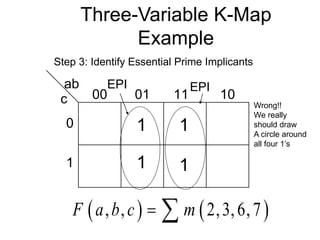
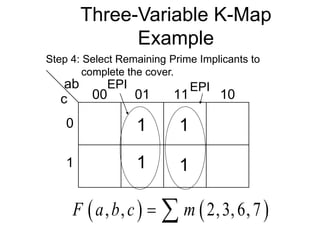
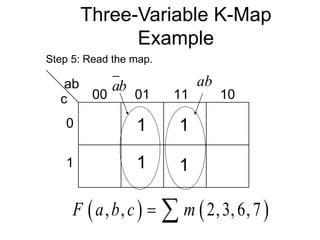
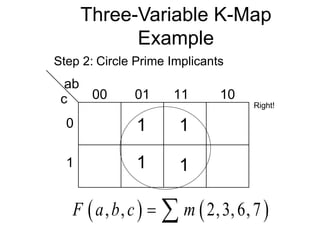
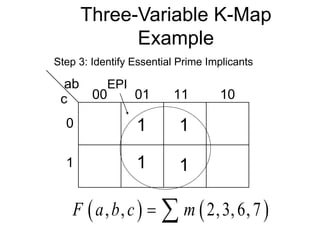
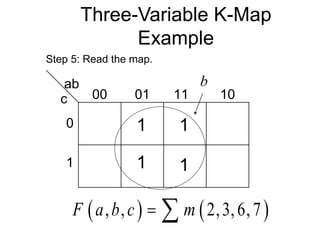
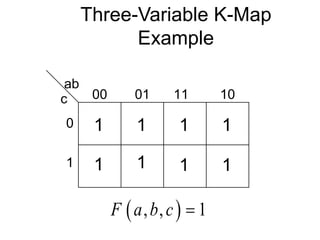
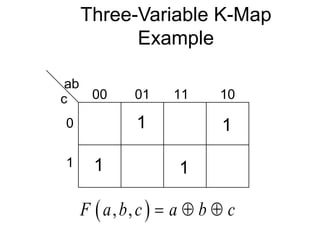
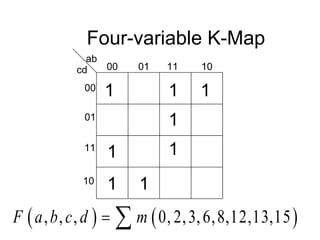
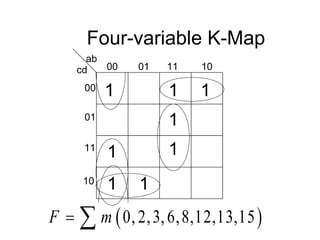
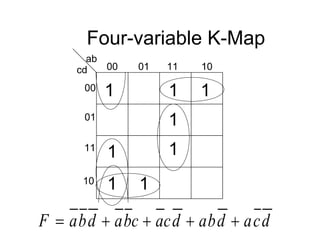
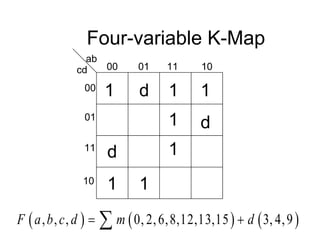
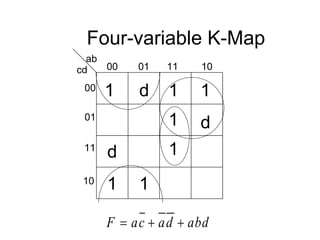
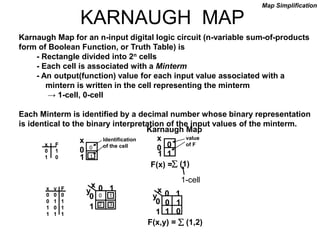
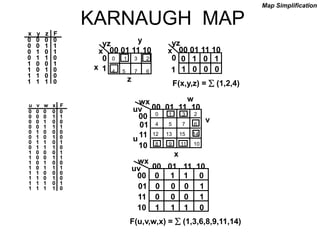
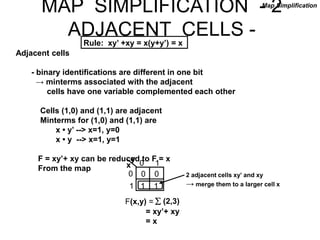
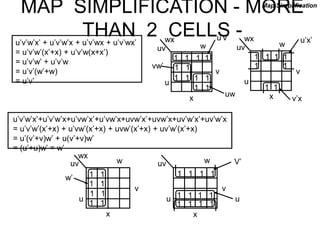
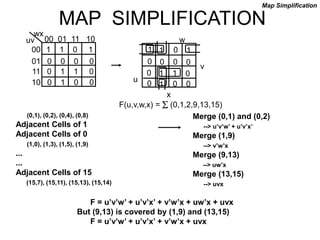
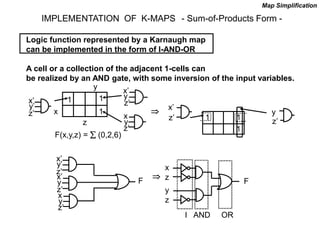
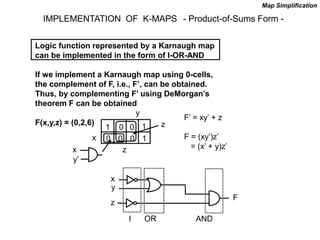
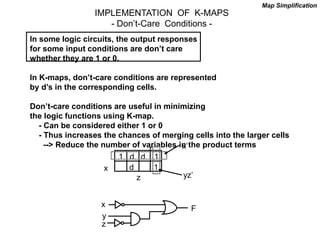
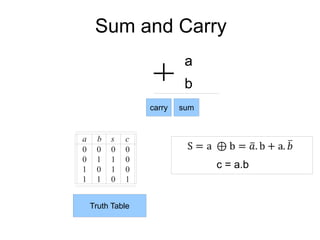
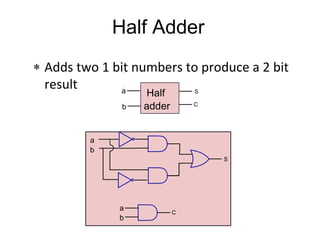
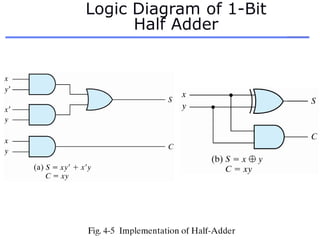
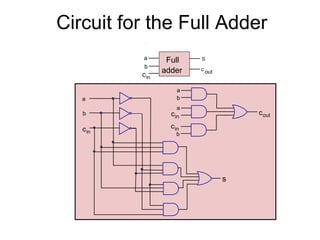
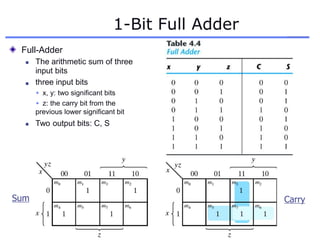
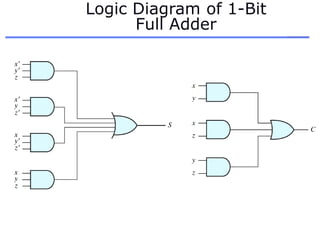
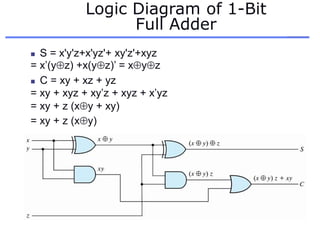
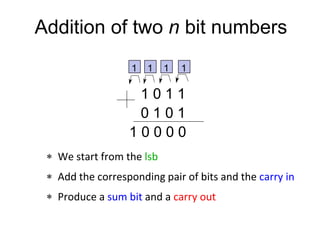
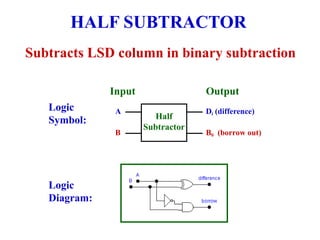
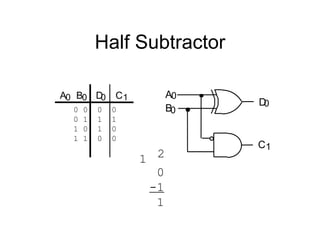
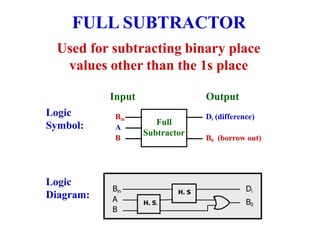
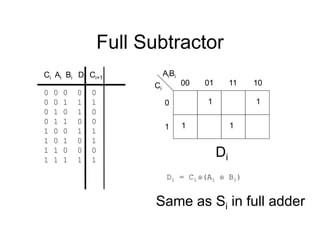
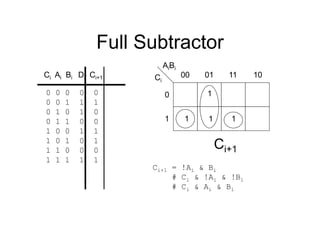
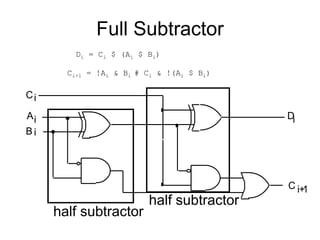
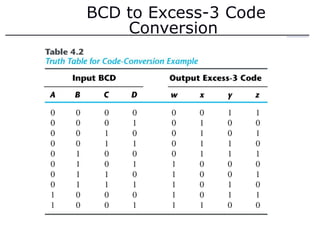
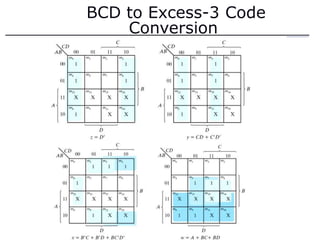
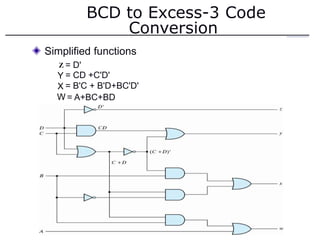
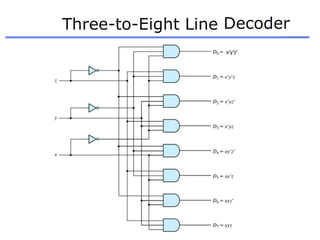
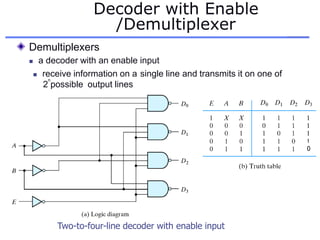
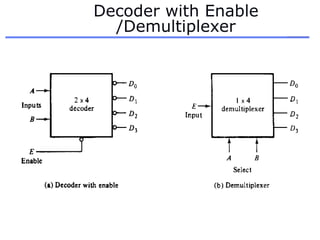
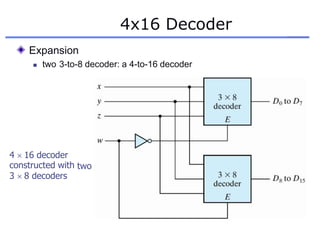
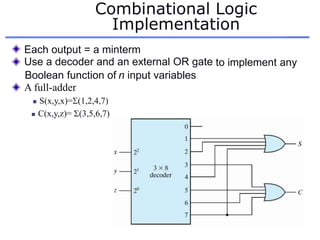
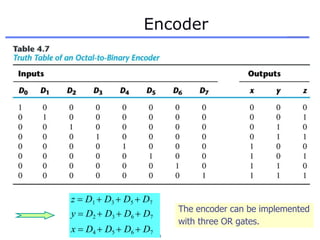
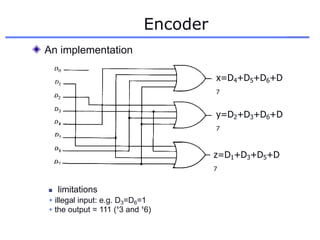
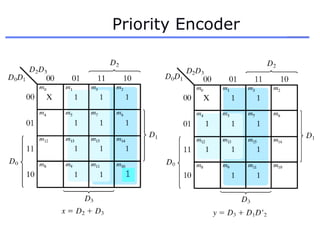
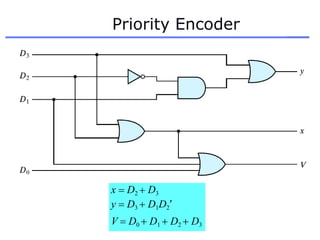
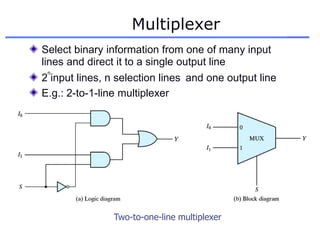
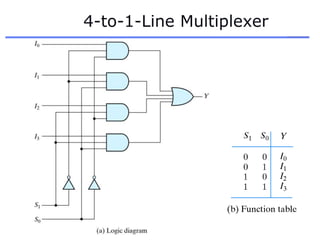
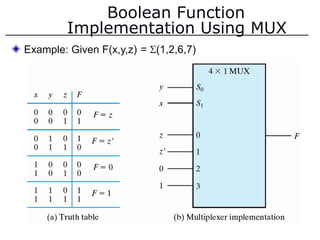
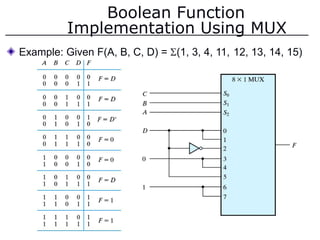
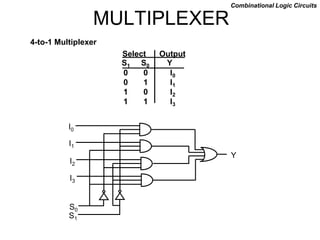
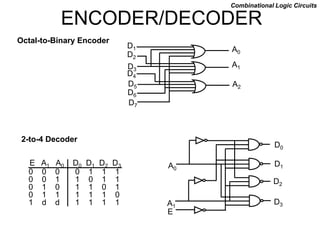
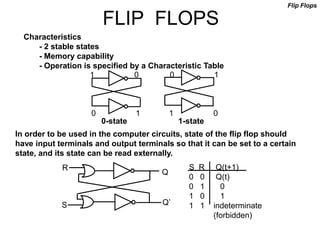
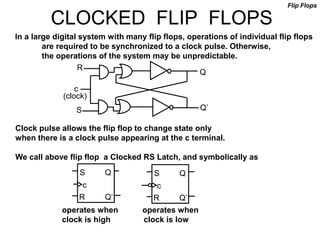
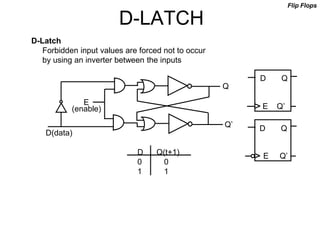
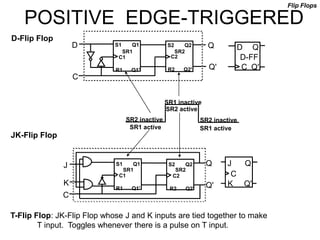
The document discusses different number systems including decimal, binary, octal, and hexadecimal. It explains how each system uses a different set of digits to represent values and how numbers are expressed as a sum of weighted place values. Conversion between different number systems like binary to decimal is demonstrated. Gray codes and binary codes for representing decimal digits are also covered. Boolean algebra concepts such as logic gates, truth tables, and identities are defined.