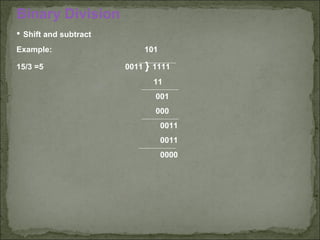
The document discusses different number systems including binary, octal, decimal, and hexadecimal. It explains that number systems have a radix or base, which determines the set of symbols used and their positional values. The key representations for binary numbers discussed are sign-magnitude, one's complement, and two's complement, which provide different methods for representing positive and negative numbers. The document provides examples of addition, subtraction, multiplication, and division operations in binary.

2. The basis for conveying & quantifying information
For exact description of any parameter, use quantities
e.g. 250
C or 300
C

3. • An ordered set of symbols
– which utilizes positional notations to represent VALUE.
• The radix (or base)
– is the total number of SYMBOLS or characters
• Example, decimal number system:
– Radix, r = 10
– Digits allowed = 0,1, 2, 3, 4, 5, 6, 7, 8, 9

4. RadixRadix (base)(base) Characters in setCharacters in set ExampleExample
22 (binary)(binary) 0,10,1 (11111111)(11111111)22
33 0,1,20,1,2
44 01,2,301,2,3
55 0,1,2,3,40,1,2,3,4
.... ....
88 (octal)(octal) 0,1,2,3,4,5,6,70,1,2,3,4,5,6,7 (377)(377)88
.... ....
1010 (decimal)(decimal) 0,1,2,3,4,5,6,7,8,90,1,2,3,4,5,6,7,8,9 (255)(255)1010
.... ....
1616 (hexadecimal)(hexadecimal) 0,1,2,3,4,5,6,7,8,9,A,B,C,0,1,2,3,4,5,6,7,8,9,A,B,C,
D,E,FD,E,F
(FF)(FF)1616

5. Distinguish-ability of symbols
Arithmetic operation capability
Number of different symbols is restricted by the base or
radix.
A special symbol is used to describe nothing (‘0’- Zero).
Every symbol has positional value in an ordered list.
The position of the symbol within the number indicates
multiplication by a relevant power of the base.

6.  The general representation of an unsigned number is with integer and
fraction portions number in a number system with radix r:
Decimal point
Integer part Fractional part
d3 d2 d1 d0. d-1 d-2 d-3
 Digit Position 3 2 1 0 -1 -2 -3
 Weight 103
102
101
100
10-1
10-2
10-3
(Exponent notation)
 Weight 1000 100 10 1 1/10 1/100 1/1000
(Value)
e.g. 273.5 = 2x103
+ 7x102
+ 3x101
+ 5 10-1
= 200+70+3+0.5

7. Well known?
Easy to use??
Every body is using???
????
Hint – Human Anatomy

8. A number representation
dp−1dp−2 ⋅⋅⋅ d1d0 . d−1d−2 ⋅⋅⋅ d−n
The value of the number is given by:
i
p
ni
i rdD ⋅= ∑
−
−=
1

9. The general form of a binary number of p+n binary
digits (bits) is:
bp−1bp−2 ⋅⋅⋅ b1b0 . b−1b−2 ⋅⋅⋅ b−n
and its value is:
i
p
ni
ibB 2
1
⋅= ∑
−
−=

10. Base- 2
Symbols – 0 & 1
Binary digIT = BIT
Binary system is popular for computers
low voltage level (0-state) and high voltage level (1-state).
On the other hand, it is impossible to represent any
other number system physically
in terms of many voltage levels and design digital system to
identify these distinct levels.

11. Positive Power of 2Positive Power of 2 Decimal numberDecimal number Negative power of 2Negative power of 2 Decimal valueDecimal value
00 11 -- --
11 22 -1-1 0.50.5
22 44 -2-2 0.250.25
33 88 -3-3 0.1250.125
44 1616 -4-4 0.06250.0625
55 3232 -5-5 0.031250.03125
66 6464 -6-6 0.0156250.015625
77 128128 -7-7 0.00781250.0078125
88 256256 -8-8 0.003906250.00390625
99 512512 -9-9 0.0019531250.001953125
1010 1024 ~ 1 K (Kilo)1024 ~ 1 K (Kilo) -10-10 0.0009765625 ~ 1 mili0.0009765625 ~ 1 mili
2020 222020
~ 1 Mega~ 1 Mega -20-20 22-20-20
~ 1 micro~ 1 micro
3030 223030
~ 1 Giga~ 1 Giga -30-30 22-30-30
~ 1 nano~ 1 nano
4040 224040
~ 1 Tera~ 1 Tera -40-40 22-40-40
~ 1 pico~ 1 pico

12. i
p
ni
ibB 2
1
⋅= ∑
−
−=
 Method: summation
Example:
101110110012 = 1 ⋅ 210
+ 0 ⋅ 29
+ 1 ⋅ 28
+ 1 ⋅ 27
+ 1 ⋅ 26
+ 0 ⋅ 25
+
1 ⋅ 24
+ 1 ⋅ 23
+ 0 ⋅ 22
+ 0 ⋅ 21
+ 1 ⋅ 20
= 149710

13. Method: successive divisions
Example:

14. EXAMPLE: convert 5310 to binary
EXAMPLE: convert .625ten to binary
EXAMPLE: convert 2314 to base 7.

15. Conversion between Number Systems
• Radix-r to decimal:
§ Multiply digits with their corresponding weights and add
• Decimal to binary (radix 2)
§ Whole numbers: repeated division by 2
§ Fractions: repeated multiplication by 2
• Decimal to radix-r
§ Whole numbers: repeated division by r
§ Fractions: repeated multiplication by r
• Binary to Octal
§ Substitute groups of three bits with corresponding octal digit.
• Binary to Hexadecimal
§ Substitute groups of four bits with corresponding hexadecimal digit.

16. A code is a symbol or group of symbols that stand for
something
Although the binary system of numbers is most
appropriate for use in computers but has several
disadvantages
 Binary machine code is long
 Difficult to assimilate
 Tedious to convert to decimal
Simpler way to represent binary numbers for conversion
to decimal representation
 Binary coded decimal (BCD) – 4 bit code
 Binary coded octal (BCO) – 3 bit code
 Binary coded hexadecimal (BCH) – 4 bit code

17. • Binary codes for simplification in representation - BCD,
BCO, BCH
• Binary codes for driving display – BCD
• Binary codes for arithmetic operations –BCD, 9’s & 10’s
complement (Self-complementing codes)
• Binary codes for creation of digital transducer – Gray code
(Unit-distance code or reflective code)
• Binary codes for transmission & reception – ASCII
• Binary codes for representing signed numbers – Sign-
magnitude, 1’s & 2’s complement

18.  The octal number system uses
radix 8, while the hexadecimal
number system uses radix 16
 The octal and hex number systems
are useful for representing multibit
numbers

19. Binary Arithmetic Operations
Addition
• Similar to decimal number addition, two binary numbers
are
added by adding each pair of bits together with carry
propagation.
• Addition Example:
1 0 1 1 1 1 0 0 0 Carry
X 190 1 0 1 1 1 1 1 0
Y 141 1 0 0 0 1 1 0 1
X + Y 331 1 0 1 0 0 1 0 1 1
+ +

20. Negative Binary Number Representations
• Signed-Magnitude Representation:
– For an n-bit binary number:
Use the first bit (most significant bit, MSB) position to
represent the sign where 0 is positive and 1 is negative.
Ex. 1 1 1 1 1 1 1 12 = - 12710
– Remaining n-1 bits represent the magnitude which may range from:
-2(n-1)
+ 1 to 2(n-1)
- 1
– This scheme has two representations for 0; i.e., both positive and
negative 0: for 8 bits: 00000000, 10000000
– Arithmetic under this scheme uses the sign bit to indicate the nature
of the operation and the sign of the result, but the sign bit is not

21. Negative Binary Number Representations
• One’s-Complement representation
• MSB is the sign (MSB = 1 indicates a negative number)
• Negative numbers are found by complementing all bits
• ex. 11910 = 01110111
-11910 = 10001000
• The range of values for an n-bit binary number in 1’s complement
representation is -2(n-1)
+1 to 2(n-1)
- 1
• One’s-complement addition/subtraction:
If there is a carry out of the sign position add 1
Ex. -2 1101
+ -5 1010
-7 10111
+ 1
1000

22. Negative Binary Number Representations
• Two’s complement representation:
• MSB is the sign (MSB = 1 indicates a negative number)
•The range for an n-bit binary number in 2’s complement representation is
from -2(n-1) to 2(n-1) - 1
• To negate a number complement all bits and add 1
• ex. 11910 = 01110111 complement bits
10001000
+ 1 add 1
100010012 = - 11910
Two’ complement addition/subtraction
Examples:
4 0100 -2 1110
+ -7 1001 + -6 1010
-3 1101 -8 1 1000
Ignore carry out from MSB

23. Binary Arithmetic Operations
Subtraction
• Two binary numbers are subtracted by subtracting
each pair of bits together with borrowing, where needed.
• Subtraction Example:
0 0 1 1 1 1 1 0 0 Borrow
X 229 1 1 1 0 0 1 0 1
Y 46 0 0 1 0 1 1 1 0
183 1 0 1 1 0 1 1 1
- -

24. Binary Multiplication
• Multiplication is achieved by adding a list of shifted multiplicands according
to the digits of the multiplier.
• Ex. (unsigned)
11 1 0 1 1 multiplicand (4 bits)
X 13 X 1 1 0 1 multiplier (4 bits)
-------- -------------------
33 1 0 1 1
11 0 0 0 0
1 0 1 1
143 1 0 1 1
---------------------
1 0 0 0 1 1 1 1 Product (8 bits)

25. Binary Division
• Shift and subtract
Example: 101
15/3 =5 0011 } 1111
11
001
000
0011
0011
0000

26. Sign- Magnitude method
1’s complement
2’s complement

27.  Representation of positive numbers same in most systems
 Major differences are in how negative numbers are represented
 Three major schemes:
 sign and magnitude
 ones complement
 twos complement
 Assumptions:
 we'll assume a 4 bit machine word
 16 different values can be represented
 roughly half are positive, half are negative

28. Sign and Magnitude Representation
0000
0111
0011
1011
1111
1110
1101
1100
1010
1001
1000
0110
0101
0100
0010
0001
+0
+1
+2
+3
+4
+5
+6
+7-0
-1
-2
-3
-4
-5
-6
-7
0 100 = + 4
1 100 = - 4
+
-
High order bit is sign: 0 = positive (or zero), 1 = negative
Three low order bits is the magnitude: 0 (000) thru 7 (111)
Number range for n bits = +/-2 -1
Representations for 0
n-1

29. Cumbersome addition/subtraction
Must compare magnitudes to determine sign of
result
Sign and Magnitude
Ones Complement
N is positive number, then N is its negative 1's complement
N = (2 - 1) - N
n
Example: 1's complement of 7
2 = 10000
-1 = 00001
1111
-7 = 0111
1000 = -7 in 1's comp.Shortcut method:
simply compute bit wise complement
0111 -> 1000
4

30. Subtraction implemented by addition & 1's complement
Still two representations of 0! This causes some problems
Some complexities in addition
Ones Complement
0000
0111
0011
1011
1111
1110
1101
1100
1010
1001
1000
0110
0101
0100
0010
0001
+0
+1
+2
+3
+4
+5
+6
+7-7
-6
-5
-4
-3
-2
-1
-0
0 100 = + 4
1 011 = - 4
+
-

31. Only one representation for 0
One more negative number than positive
number
Twos Complement
0000
0111
0011
1011
1111
1110
1101
1100
1010
1001
1000
0110
0101
0100
0010
0001
+0
+1
+2
+3
+4
+5
+6
+7-8
-7
-6
-5
-4
-3
-2
-1
0 100 = + 4
1 100 = - 4
+
-
like 1's comp
except shifted
one position
clockwise

32. Twos Complement Numbers
N* = 2 - N
n
Example: Twos complement of 7
2 = 10000
7 = 0111
1001 = repr. of -7
Example: Twos complement of -7
4
2 = 10000
-7 = 1001
0111 = repr. of 7
4
sub
sub
Shortcut method:
Twos complement = bitwise complement + 1
0111 -> 1000 + 1 -> 1001 (representation of -7)
1001 -> 0110 + 1 -> 0111 (representation of 7)

33. Addition and Subtraction of Numbers
Sign and Magnitude
4
+ 3
7
0100
0011
0111
-4
+ (-3)
-7
1100
1011
1111
result sign bit is the
same as the operands'
sign
4
- 3
1
0100
1011
0001
-4
+ 3
-1
1100
0011
1001
when signs differ,
operation is subtract,
sign of result depends
on sign of number with
the larger magnitude

34. Addition and Subtraction of Numbers
Ones Complement Calculations
4
+ 3
7
0100
0011
0111
-4
+ (-3)
-7
1011
1100
10111
1
1000
4
- 3
1
0100
1100
10000
1
0001
-4
+ 3
-1
1011
0011
1110
End around carry
End around carry

35. Addition and Subtraction of Binary Numbers
Ones Complement Calculations
Why does end-around carry work?
Its equivalent to subtracting 2 and adding 1
n
M - N = M + N = M + (2 - 1 - N) = (M - N) + 2 - 1
n n
(M > N)
-M + (-N) = M + N = (2 - M - 1) + (2 - N - 1)
= 2 + [2 - 1 - (M + N)] - 1
n n
n n
M + N < 2
n-1
after end around carry:
= 2 - 1 - (M + N)
n
this is the correct form for representing -(M + N) in 1's comp!

36. Addition and Subtraction of Binary Numbers
Twos Complement Calculations
4
+ 3
7
0100
0011
0111
-4
+ (-3)
-7
1100
1101
11001
4
- 3
1
0100
1101
10001
-4
+ 3
-1
1100
0011
1111
If carry-in to sign =
carry-out then ignore
carry
if carry-in differs from
carry-out then overflow
Simpler addition scheme makes twos complement the most common
choice for integer number systems within digital systems

37. Addition and Subtraction of Binary Numbers
Twos Complement Calculations
Why can the carry-out be ignored?
-M + N when N > M:
M* + N = (2 - M) + N = 2 + (N - M)
n n
Ignoring carry-out is just like subtracting 2
n
-M + -N where N + M < or = 2
n-1
-M + (-N) = M* + N* = (2 - M) + (2 - N)
= 2 - (M + N) + 2
n n
After ignoring the carry, this is just the right twos compl.
representation for -(M + N)!
n n

38. Overflow Conditions
Add two positive numbers to get a negative number
or two negative numbers to get a positive number
5 + 3 = -9 -7 - 2 = +7
0000
0001
0010
0011
1000
0101
0110
0100
1001
1010
1011
1100
1101
0111
1110
1111
+0
+1
+2
+3
+4
+5
+6
+7-8
-7
-6
-5
-4
-3
-2
-1
0000
0001
0010
0011
1000
0101
0110
0100
1001
1010
1011
1100
1101
0111
1110
1111
+0
+1
+2
+3
+4
+5
+6
+7-8
-7
-6
-5
-4
-3
-2
-1

39. Overflow Conditions
5
3
-8
0 1 1 1
0 1 0 1
0 0 1 1
1 0 0 0
-7
-2
7
1 0 0 0
1 0 0 1
1 1 0 0
1 0 1 1 1
5
2
7
0 0 0 0
0 1 0 1
0 0 1 0
0 1 1 1
-3
-5
-8
1 1 1 1
1 1 0 1
1 0 1 1
1 1 0 0 0
Overflow Overflow
No overflow No overflow
Overflow when carry in to sign does not equal carry out

40. Thank You.