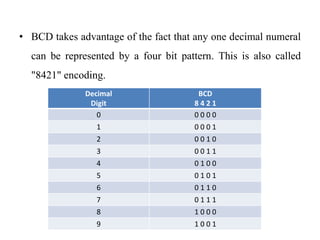
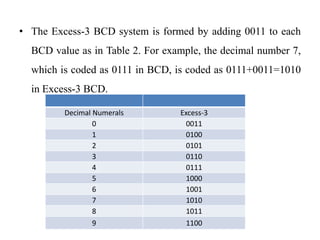
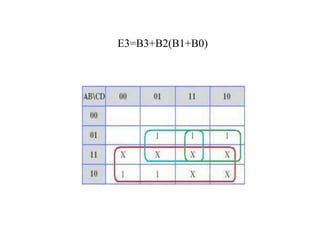
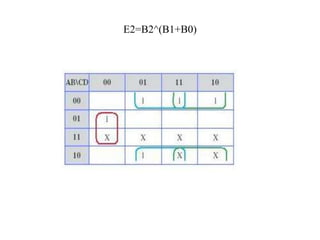
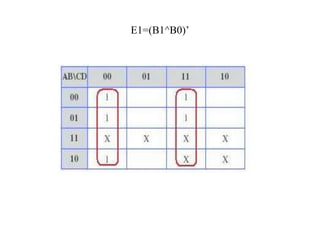
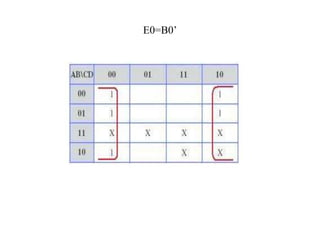
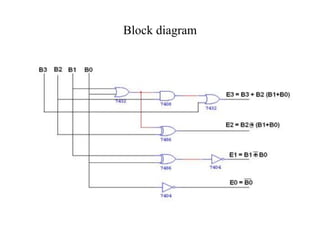
This document describes a circuit to convert between binary coded decimal (BCD) and excess-3 code. It begins by explaining that code converters are needed when different systems use different codes to represent the same information. It then provides background on BCD, which represents each decimal digit with 4 bits, and excess-3 code, which adds 0011 to each BCD value. The document presents the truth table for the conversion and uses Karnaugh maps to derive the Boolean expressions for converting each output bit. It concludes by mentioning some early applications of excess-3 code in computers, cash registers and calculators.

1. BCD to EXCESS 3 Code Converter
By
Ushaswini chowdary.M

2. Introduction
• The availability of large variety of codes for the same discrete
elements of information results in the use of different codes by
the different systems.
• A conversion circuit must be inserted between the two systems
if each use different codes for the same information.
• Thus a code converter is a circuit that makes the two systems
compatible even though both uses different binary
information.

3. • Code converters, more specifically encoders and decoders,
have been used to protect private information.
• Indeed, code converters have proven to be so effective that the
National Security Agency (NSA) has made a career out of
creating and breaking codes.
• To convert from binary to excess 3 code the input lines must
supply the bit combination of elements as specified by the
code.

4. Binary Coded Decimal
• The term BCD refers to representing the ten decimal digits in
binary forms; which simply means to count in binary.
• In computing and electronic systems, binary coded decimal is
a class of binary encodings of decimal numbers where each
decimal digit is represented by a fixed number of bits , usually
four or eight, although other sizes (such as six bits) have been
used historically. Special bit patterns are sometimes used for
a sign or for other indications (e.g., error or overflow).

5. • BCD takes advantage of the fact that any one decimal numeral
can be represented by a four bit pattern. This is also called
"8421" encoding.
Decimal
Digit
BCD
8 4 2 1
0 0 0 0 0
1 0 0 0 1
2 0 0 1 0
3 0 0 1 1
4 0 1 0 0
5 0 1 0 1
6 0 1 1 0
7 0 1 1 1
8 1 0 0 0
9 1 0 0 1

6. Excess 3
• It is a non weighted code.
• In XS-3, numbers are represented as decimal digits, and each
digit is represented by four bits as the digit value plus 3 (the
"excess" amount).
• The primary advantage of XS-3 coding over non-biased
coding is that a decimal number can be nines' complemented
as easily as a binary number can be ones' complemented . In
addition, when the sum of two XS-3 digits is greater than 9,
the carry bit of a four bit adder will be set high.

7. • The Excess-3 BCD system is formed by adding 0011 to each
BCD value as in Table 2. For example, the decimal number 7,
which is coded as 0111 in BCD, is coded as 0111+0011=1010
in Excess-3 BCD.
Decimal Numerals Excess-3
0 0011
1 0100
2 0101
3 0110
4 0111
5 1000
6 1001
7 1010
8 1011
9 1100

8. THE BCD TO EXCESS 3 CODE CONVERTER
• BCD Excess-3 circuit will convert numbers from their binary
representation to their excess-3 representation. Hence our truth
table is as below:
B3 B2 B1 B0 E3 E2 E1 E0
0 0 0 0 0 0 1 1
0 0 0 1 0 1 0 0
0 0 1 0 0 1 0 1
0 0 1 1 0 1 1 0
0 1 0 0 0 1 1 1
0 1 0 1 1 0 0 0
0 1 1 0 1 0 0 1
0 1 1 1 1 0 1 0
1 0 0 0 1 0 1 1
1 0 0 1 1 1 0 0

9. K maps
• Our task now is to use the truth table to find four switching
expressions: one for E3, one for E2, one for E1, and one for E0.
We have two choices: we can use Boolean algebraic
manipulations, or we can use Karnaugh maps.
• We use k maps for simplicity. Here don’t cares are available
because in the truth table in Table 3, no BCD valuations exist
for E3E2E1E0 = 1010,1011,1100,1101,1110,1111. As such, we
evaluate B3B2B1B0= xxxx (either 0 or 1).

10. E3=B3+B2(B1+B0)

11. E2=B2^(B1+B0)

12. E1=(B1^B0)’

13. E0=B0’

14. Block diagram

15. Applications
• Excess-3 was used on some older computers
• Cash registers
• Hand held portable electronic calculators