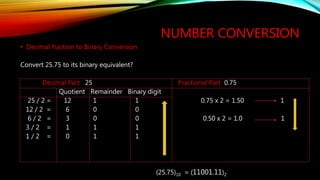
The document discusses computer memory structures and data storage units. It begins by defining basic memory units like bits, bytes and words. It then explains progressively larger units of data storage from kilobytes to yottabytes. The document also covers number systems, specifically decimal and binary. It provides examples of converting between binary, decimal and decimal fraction numbers. Conversions include binary to decimal, decimal to binary, and binary fraction to decimal fraction.

1. UGC NET- ICT
MEMORY AND DATA
Megha V
Research Scholar
Kannur University

2. MEMORY STRUCTURE
Bit (Binary Digit) – A binary digit is logical 0 and 1
Nibble- A group of 4 bits
Byte – A group of 8 bits
Word - A group of fixed number of bits processed as a unit
- varies from computer to computer
By grouping bits together we can store more values
• 8 bits = 1 byte
• 16 bits = 2 bytes = 1 halfword
• 32 bits = 4 bytes = 1 word

3. LARGER UNITS OF INFORMATION STORAGE
• 1 Kilobyte (KB) = 210 bytes = 1,024 bytes
• 1 MegabByte (MB) = 1,024 KB = 220 bytes = 1 Million bytes
• 1 Gigabyte (GB) = 1,024 MB = 230 bytes = 1 Billion bytes
• 1 Terabyte(TB)=1024 GB =240 bytes = 1 Trillion bytes
• 1 Petabyte (PB)=1024 TB = 250 bytes = 1 quadrillion bytes
• 1 Exabyte(EB) =1024 PB= 260 bytes = 1 quintillion bytes
• 1 Zettabyte (ZB) = 1024 EB = 270 bytes = 1 sextillion bytes
• 1 Yottabyte (YB) = 1024 ZB= 280 bytes = 1 septillion bytes

4. NUMBER SYSTEM
Decimal (base-10) number system
• We have symbols (digits) that can represent ten integer values: 0, 1, 2, 3, 4, 5, 6, 7, 8,
9
• We represent integer values larger than 9 with combinations of two or more digits,
e.g.: 10, 11, 12, ..., 112, ..., 247
e.g.: 247
= (7 x 100 ) + (4 x 101 ) + (2 x 102 )
2 is the Most Significant Digit
7 is the Least Significant Digit

5. NUMBER SYSTEM
Binary (Base 2) Number system
• Computer systems store information electronically using bits (binary digits)
• Each bit can be in one of two states, which we can take to represent the binary (base-2)
digits 0 and 1
• The binary number system is a natural number system for computing (rather than the
decimal system)
• Using a single bit, we can represent integer values 0 and 1
• Using two bits, we can represent 0, 1, 10, 11

6. NUMBER CONVERSION
• Binary to Decimal Conversion
100101 = (1 x 20 ) +
(0 x 21 ) + LSB - Least Significant Bit
MSB LSB (1 x 22 ) + MSB – Most Significant Bit
(0 x 23 ) +
(0 x 24 ) +
(1 x 25 ) +
= 37 (100101)2 = (37)10

7. • Binary fraction to Decimal Conversion
NUMBER CONVERSION
11001.11
decimal part 11001= fractional part .11 =
( 1 x 20 ) = 1+ (1 x 2 -1 ) + = 0.50 +
( 0 x 21 ) = 0+ (1 x 2 -2 ) = 0.25
( 0 x 22 ) = 0 +
( 1x 23 ) = 8 + = .75
( 1 x 24 ) = 16
= 25
(11001.11)2 = (25.75)10

8. NUMBER CONVERSION
• Decimal to Binary Conversion
Convert 37 to its binary equivalent?
Quotient Remainder Binary digit
37 / 2 = 18 1 1
18 / 2 = 9 0 0
9 / 2 = 4 1 1
4 / 2 = 2 0 0
2 / 2 = 1 0 0
1 / 2 = 0 1 1 (37)10 = (100101)2

9. NUMBER CONVERSION
• Decimal fraction to Binary Conversion
Convert 25.75 to its binary equivalent?
Decimal Part 25 Fractional Part 0.75
Quotient Remainder Binary digit
25 / 2 = 12 1 1 0.75 x 2 = 1.50 1
12 / 2 = 6 0 0
6 / 2 = 3 0 0 0.50 x 2 = 1.0 1
3 / 2 = 1 1 1
1 / 2 = 0 1 1
(25.75)10 = (11001.11)2