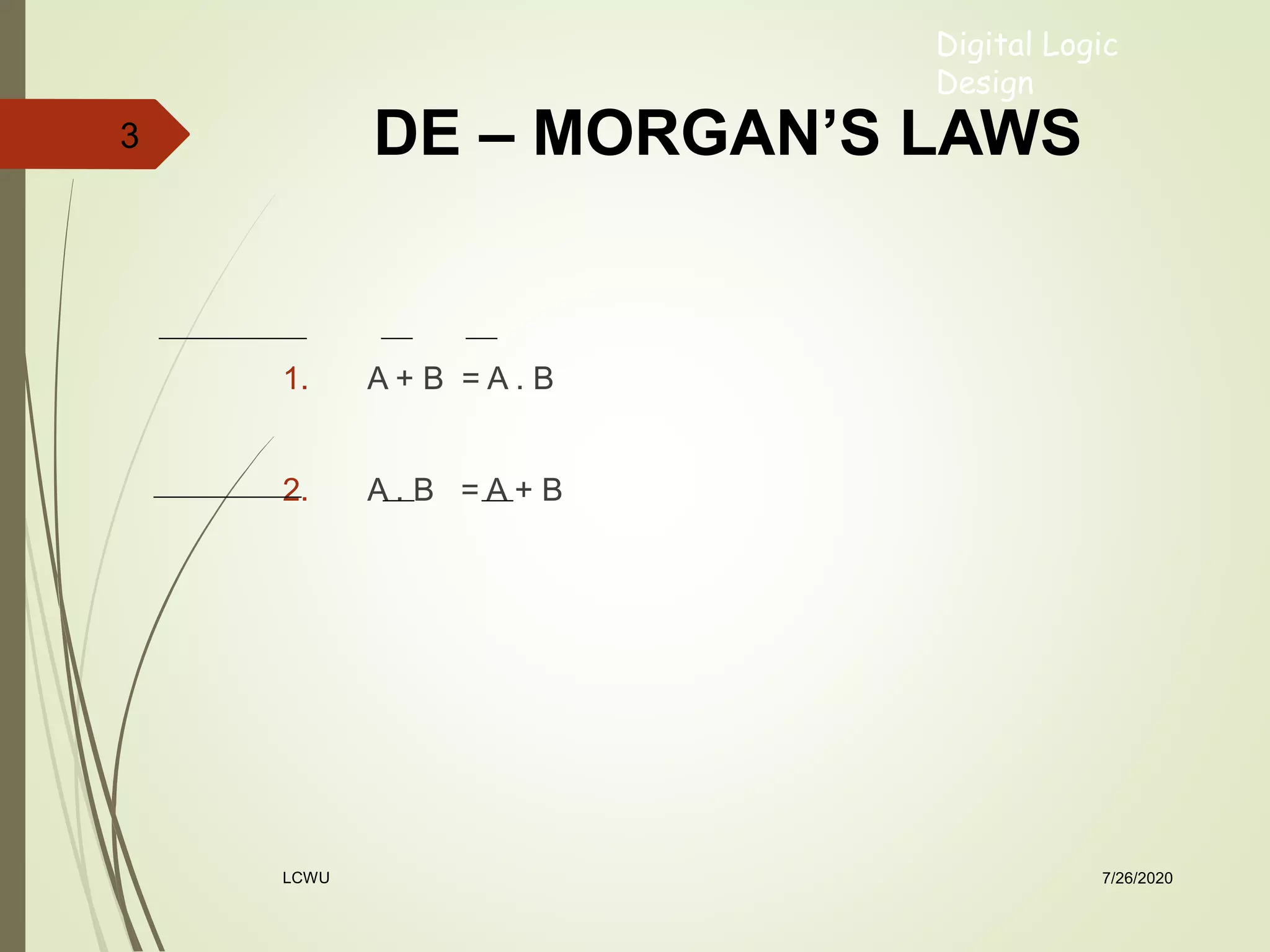
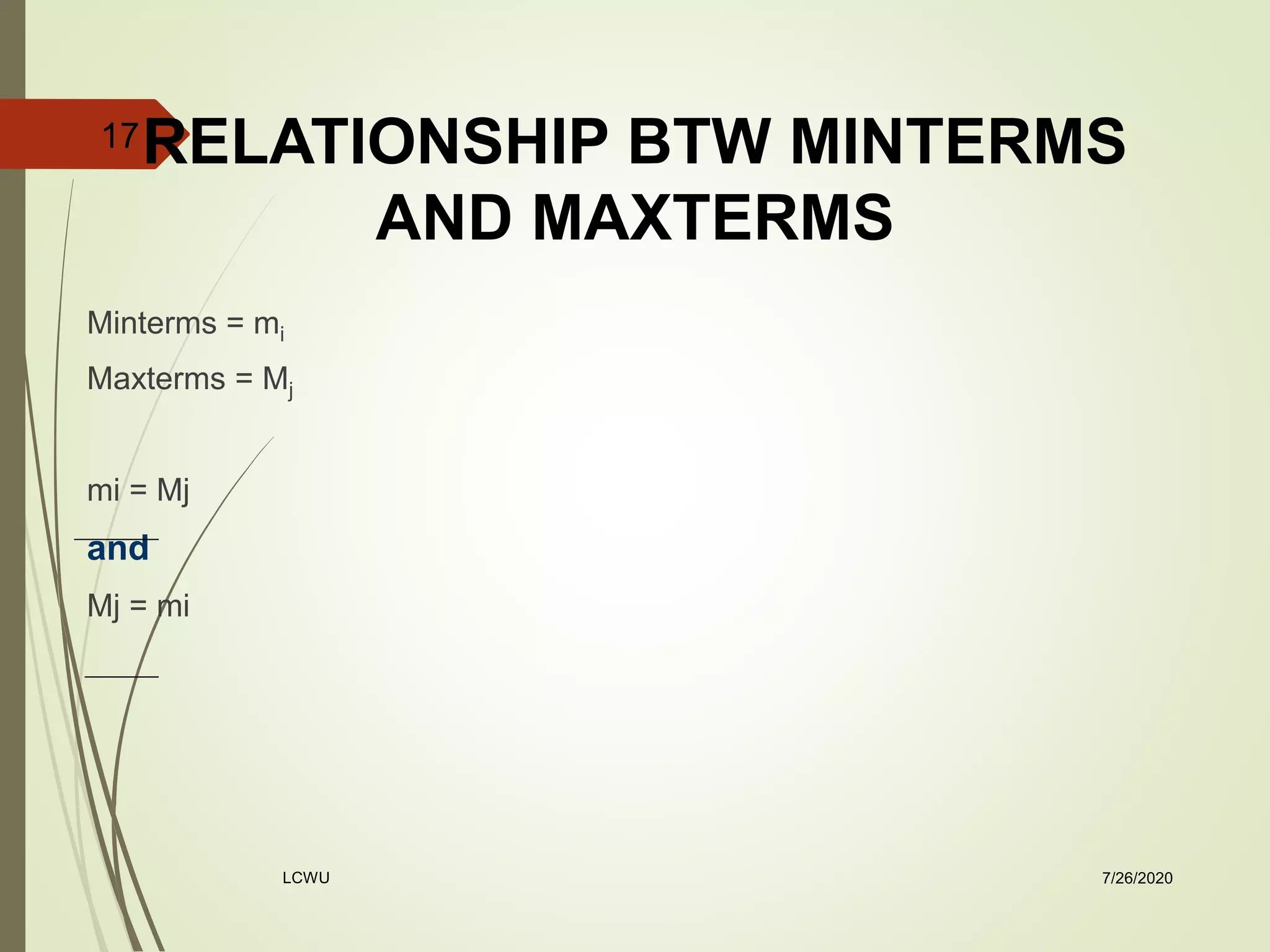
This document discusses Boolean algebra and logic gates. It defines the complement of a function as changing all 0s to 1s and vice versa. De Morgan's laws are introduced, which allow complementing both sides of an equation. Circuits are represented using diagrams of logic gates and their inputs and outputs. Standard forms for representing Boolean expressions include sum of minterms and product of maxterms, which are defined as the ANDing and ORing of variables respectively. Minterms and maxterms are demonstrated using truth tables for two variables. The relationship between minterms and maxterms is that each equals the complement of the other.

1. 7/26/2020LCWU
1
CHAPTER - 2
BOOLEAN ALGEBRA &
LOGIC GATES

2. COMPLEMENT OF A FUNCTION
 The complement of a function F is F′
 Obtained by Changing every 0 to 1 and every 1 to 0
 Derived by using De-Morgan’s Laws
7/26/2020LCWU
2
Digital Logic
Design

3. DE – MORGAN’S LAWS
1. A + B = A . B
2. A . B = A + B
7/26/2020LCWU
3
Digital Logic
Design

4. EXAMPLE
F = x′.y.z′ + x′.y′.z
Complementing BOTH sides:
F = x′.y.z′ + x′.y′.z
Applying De-Morgan’s Laws:
= (x′.y.z′) . (x′.y′.z)
= (x′′ + y′ + z′′) . (x′′ + y′′ + z′)
= (x + y′ + z) . (x + y + z′)
7/26/2020LCWU
4
Digital Logic
Design

5. CIRCUIT DIAGRAM
7/26/2020LCWU
5
Digital Logic
Design
.
.
.
.Logic
Circuit
Inputs Outputs

6. EXAMPLES
Find the Complement and reduce them to a
minimum no. of literals:
 F1 = x + x.y
 F2 = AB′ + C′D′
 G = x.y + x.y′ + y′.z
7/26/2020LCWU
6
Digital Logic
Design

7. HOMEWORK
 Example 2.2 – 2.3
 Problem 2.7
7/26/2020LCWU
7
Digital Logic
Design

8. READING MATERIAL *extra’s
Applications Of Boolean Functions – Circuit Chip
Design
QUESTION
A fire sprinkler system should spray water if high heat
is sensed and the system is set to enabled.
ANSWER
Let Boolean variable h represent “high heat is sensed,” e
represent “enabled,” and F represent “spraying water.”
Then an equation is:
F = h AND e
Symbolically, F = h . e
7/26/2020LCWU
8
Digital Logic
Design
h
e
F

9. SEAT BELT WARNING LIGHT
SYSTEMDesign circuit for warning light
• Sensors
s=1: seat belt fastened
k=1: key inserted
p=1: person in seat
Capture Boolean equation
person in seat, and seat belt not
fastened, and key inserted
• Convert equation to circuit
7/26/2020LCWU
9
Digital Logic
Design
w = p AND NOT (s) AND k

10. REPRESENTATION OF BOOLEAN
EXPRESSIONS
 Canonical Forms (Not Simplified)
 Standard Forms (Simplified)
7/26/2020LCWU
10

11. CANONICAL FORMS
 Directly obtained from the Truth table
 Not Simplified
 Two types:
SUM of MINTERMS
PRODUCT of MAXTERMS
7/26/2020LCWU
11

12. MINTERMS
 Obtained by AND-ing all variables
 1 = variables without bar/prime
 0 = variables with bar/prime
NOTE:
Each Minterm must contain all variables !!
7/26/2020LCWU
12

13. Example
Variables = x , y
Possible Combinations
= 22 = 4
Index Bin Val Minterms MVal
0 00 x’ . y’ m0
1 01 x’ . y m1
2 10 x . y’ m2
3 11 x . y m3
7/26/2020LCWU
13

14.  4 Minterms for 2 variables.
 ? Minterms for 3 variables.
 ? Minterms for 4 variables.
7/26/2020LCWU
14

15. MAXTERMS
 Obtained by OR-ing all variables
 1 = variables with bar/prime
 0 = variables without bar/prime
NOTE:
Each Maxterm must contain all variables !!
7/26/2020LCWU
15

16. Example
Variables = x , y
Possible Combinations
= 22 = 4
Index Bin Val Maxterms MVal
0 00 x + y M0
1 01 x + y’ M1
2 10 x’ + y M2
3 11 x’ + y’ M3
7/26/2020LCWU
16

17. RELATIONSHIP BTW MINTERMS
AND MAXTERMS
Minterms = mi
Maxterms = Mj
mi = Mj
and
Mj = mi
7/26/2020LCWU
17