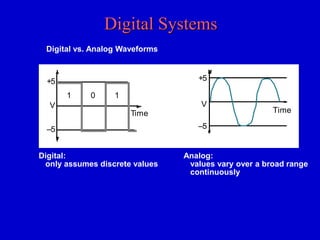
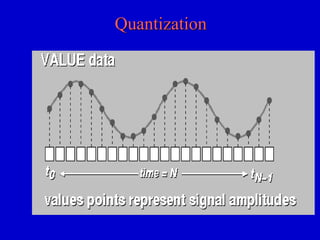
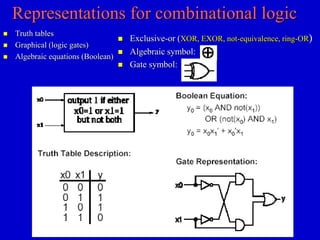
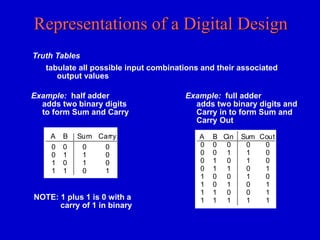
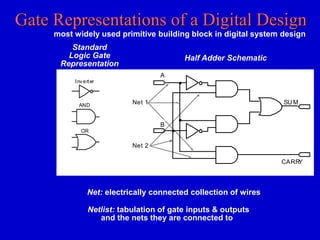
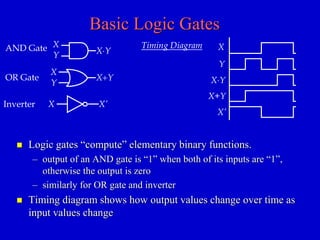
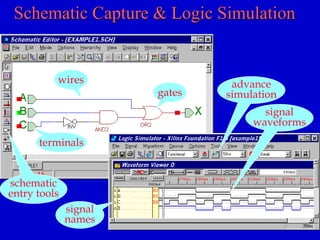
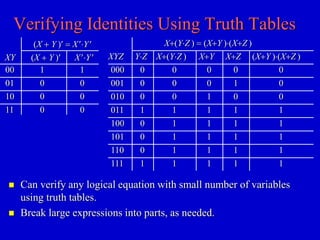
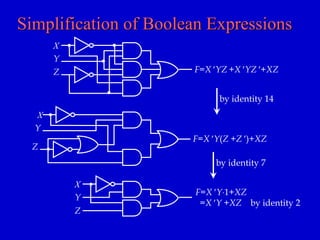
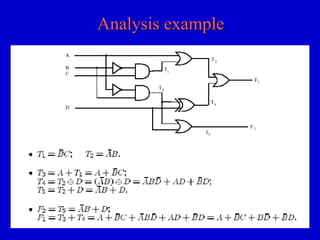
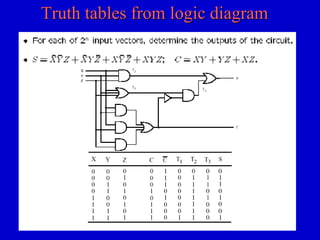
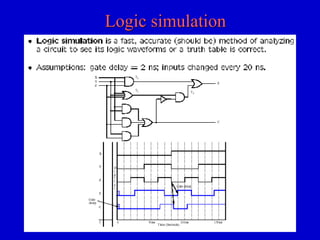
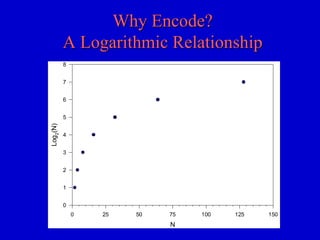
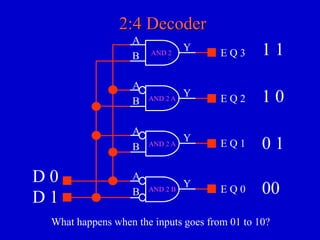
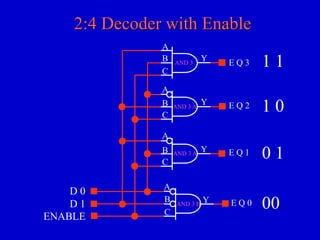
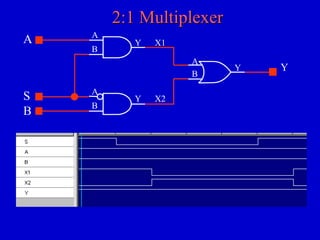
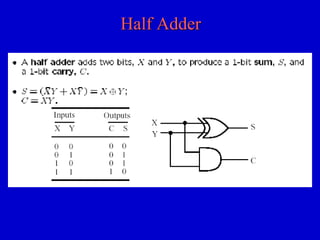
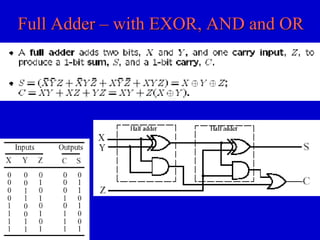
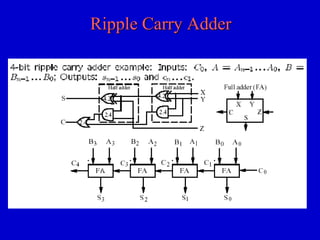
This document provides an overview of digital logic circuits and digital systems. It discusses binary logic, logic gates like NAND and NOR, Boolean algebra, decoders, adders, and the differences between analog and digital signals. It also covers representations of digital designs using truth tables, Boolean algebra, logic gate schematics, and logic simulations. Common logic gates, functions, identities, simplification techniques, and the duality principle of Boolean algebra are described.

1. Digital Logic Circuits
 Binary Logic and Gates
 Logic Simulation
 Boolean Algebra
 NAND/NOR and XOR gates
 Decoder fundamentals
 Half Adder, Full Adder, Ripple Carry Adder

2. Analog vs Digital
 Analog
– Continuous
» Time
 Every time has a value associated with it, not just some times
» Magnitude
 A variable can take on any value within a range
» e.g.
 temperature, voltage, current, weight, length, brightness, color

3. Digital Systems
Digital vs. Analog Waveforms
Analog:
values vary over a broad range
continuously
Digital:
only assumes discrete values
+5
V
–5
T ime
+5
V
–5
1 0 1
T ime

4. Quantization

5. Analog vs Digital
 Digital
– Discontinuous
» Time (discretized)
 The variable is only defined at certain times
» Magnitude (quantized)
 The variable can only take on values from a finite set
» e.g.
 Switch position, digital logic, Dow-Jones Industrial, lottery, batting-average

6. Analog to Digital
 A Continuous Signal is Sampled at Some Time and Converted to a
Quantized Representation of its Magnitude at that Time
– Samples are usually taken at regular intervals and controlled by a
clock signal
– The magnitude of the signal is stored as a sequence of binary valued
(0,1) bits according to some encoding scheme

7. Digital to Analog
 A Binary Valued, B = { 0, 1 }, Code Word can be Converted to its
Analog Value
 Output of D/A Usually Passed Through Analog Low Pass Filter to
Approximate a Continuous Signal
 Many Applications Construct a Signal Digitally and then D/A
– e.g., RF Transmitters, Signal Generators

8. Digital is Ubiquitous
 Electronic Circuits based on Digital Principles are Widely Used
– Automotive Engine/Speed Controllers
– Microwave Oven Controllers
– Heating Duct Controls
– Digital Watches
– Cellular Phones
– Video Games

9. Why Digital?
 Increased Noise Immunity
 Reliable
 Inexpensive
 Programmable
 Easy to Compute Nonlinear Functions
 Reproducible
 Small

10. Digital Design Process
 Computer Aided Design Tools
– Design entry
– Synthesis
– Verification and simulation
– Physical design
– Fabrication
– Testing

11. Definition

12. Representations for combinational logic
 Exclusive-or (XOR, EXOR, not-equivalence, ring-OR)
 Algebraic symbol:
 Gate symbol:
 Truth tables
 Graphical (logic gates)
 Algebraic equations (Boolean)

13. Boolean algebra & logic circuits

14. Representations of a Digital Design
Truth Tables
tabulate all possible input combinations and their associated
output values
Example: half adder
adds two binary digits
to form Sum and Carry
Example: full adder
adds two binary digits and
Carry in to form Sum and
Carry Out
A B
0
0
0
1
1
0
1
1
Sum Carry
0
0
1
0
1
0
0
1
NOTE: 1 plus 1 is 0 with a
carry of 1 in binary
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C in
0
1
0
1
0
1
0
1
S um
0
1
1
0
1
0
0
1
C out
0
0
0
1
0
1
1
1

15. Representations of Digital Design:
Boolean Algebra
values: 0, 1
variables: A, B, C, . . ., X, Y, Z
operations: NOT, AND, OR, . . .
NOT X is written as X
X AND Y is written as X & Y, or sometimes X Y
X OR Y is written as X + Y
Deriving Boolean equations from truth tables:
A
0
0
1
1
B
0
1
0
1
Sum
0
1
1
0
Carry
0
0
0
1
Sum = A B + A B
Carry = A B
OR'd together product terms
for each truth table
row where the function is 1
if input variable is 0, it appears in
complemented form;
if 1, it appears uncomplemented

16. Representations of a Digital
Design: Boolean Algebra
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
Cin
0
1
0
1
0
1
0
1
Sum
0
1
1
0
1
0
0
1
Cout
0
0
0
1
0
1
1
1
Another example:
Sum = A B Cin + A B Cin + A B Cin + A B Cin
Cout = A B Cin + A B Cin + A B Cin + A B Cin

17. Gate Representations of a Digital Design
most widely used primitive building block in digital system design
Standard
Logic Gate
Representation
Half Adder Schematic
Net: electrically connected collection of wires
Netlist: tabulation of gate inputs & outputs
and the nets they are connected to
Inv erter
AND
OR
Net 1
Net 2
A
B
SUM
CARRY

18. Design methodology

19. Top-down vs. bottom-up design

20. Analysis procedures

21. Schematic for 4 Bit ALU
AN
D
Gate
EXO
R
Gate
OR
Gate
Inverto
r

22. Simulation of 4 Bit ALU
if S=0 then D=B-A
if S=1 then D=A-B
if S=2 then D=A+B
A
B
D
4
2
4
S if S=3 then D=-A

23. Elementary Binary Logic Functions
 Digital circuits represent information using two voltage levels.
– binary variables are used to denote these values
– by convention, the values are called “1” and “0” and we often think of
them as meaning “True” and “False”
 Functions of binary variables are called logic functions.
– AND(A,B) = 1 if A=1 and B=1, else it is zero.
» AND is generally written in the shorthand AB (or A&B or AB)
– OR(A,B) = 1 if A=1 or B=1, else it is zero.
» OR is generally written in the shorthand form A+B (or A|B or AB)
– NOT(A) = 1 if A=0 else it is zero.
» NOT is generally written in the shorthand form (or A or A) A
 AND, OR and NOT can be used to express all other logic functions.

24. Two Variable Binary Logic Functions
ZERO
0
0
0
0
A
0
0
1
1
B
0
1
0
1
 Can make similar truth tables for 3 variable or 4 variable functions,
but gets big (256 & 65,536 columns).
NOR
1
0
0
0
A
1
1
0
0
(BA)
0
1
0
0
(AB)
0
0
1
0
B
1
0
1
0
NAND
1
1
1
0
EXOR
0
1
1
0
AND
0
0
0
1
EQUAL
1
0
0
1
AB
1
1
0
1
B
0
1
0
1
A
0
0
1
1
BA
1
0
1
1
ONE
1
1
1
1
OR
0
1
1
1
 Representing functions in terms of AND, OR, NOT.
– NAND(A,B) = (AB)
– EXOR(A,B) = (AB) + (AB )

25. Basic Logic Gates
X
Y AND Gate XY
X+Y
X
Y
OR Gate
Inverter X X’
X
Y
XY
X+Y
 Logic gates “compute” elementary binary functions.
– output of an AND gate is “1” when both of its inputs are “1”,
otherwise the output is zero
– similarly for OR gate and inverter
 Timing diagram shows how output values change over time as
input values change
X’
Timing Diagram

26. Multivariable Gates
3 input AND Gate
6 input OR Gate
 AND function on n variables is “1” if and only if ALL its
arguments are “1”.
– n input AND gate output is “1” if all inputs are “1”
 OR function on n variables is “1” if and only if at least one of its
arguments is “1”.
– n input OR gate output is “1” if any inputs are “1”
 Can construct “large” gates from 2 input gates.
– however, large gates can be less expensive than required number of 2
input gates
ABC
A+B+C+D+E+F
A
B
C
A
C B
D
F E

27. Elements of Boolean Algebra
 Boolean algebra defines rules for manipulating symbolic binary logic
expressions.
– a symbolic binary logic expression consists of binary variables and the
operators AND, OR and NOT (e.g. A+BC)
 The possible values for any Boolean expression can be tabulated in a
truth table.
A B C BC A+BC
0
0
0
0
0
0
0
1
0
0
0
1
0
1
1
0
1
1
0
0
1
0
0
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
1
A
B
C
A+BC
 Can define circuit for
expression by combining
gates.

28. Schematic Capture & Logic Simulation
gates
wires
terminals
schematic
entry tools
signal
waveforms
signal
names
advance
simulation

29. Boolean Functions to Logic Circuits
 Any Boolean expression can be converted to a logic circuit made up of
AND, OR and NOT gates.
step 1: add parentheses to expression to fully define order of
operations - A+(B(C))
step 2: create gate for “last” operation in expression
gate’s output is value of expression
gate’s inputs are expressions combined by operation
A
A+BC
(B(C))
step 3: repeat for sub-expressions and continue until done
 Number of simple gates needed to implement expression equals
number of operations in expression.
– so, simpler equivalent expression yields less expensive circuit
– Boolean algebra provides rules for simplifying expressions

30. Basic Identities of Boolean Algebra
1. X + 0 = X
3. X + 1 = 1
5. X + X = X
7. X + X ’ = 1
9. (X ’)’ = X
10. X + Y = Y + X
12. X+(Y+Z ) = (X+Y )+Z
14. X(Y+Z ) = XY + XZ
16. (X + Y ) = X Y 
2. X1 = X
4. X0 = 0
6. XX = X
8. XX ’ = 0
11. XY = YX
13. X(YZ ) = (XY )Z
15. X+(YZ ) = (X+Y )(X+Z )
17. (XY)’ = X +Y 
commutative
associative
distributive
DeMorgan’s
 Identities define intrinsic properties of Boolean algebra.
 Useful in simplifying Boolean expressions
 Note: 15-17 have no counterpart in ordinary algebra.
 Parallel columns illustrate duality principle.

31. Verifying Identities Using Truth Tables
X+(YZ ) = (X+Y )(X+Z )
YZ
0
0
0
1
0
0
0
1
XYZ
000
001
010
011
100
101
110
111
X+(YZ )
0
0
0
1
1
1
1
1
X+Y
0
0
1
1
1
1
1
1
 Can verify any logical equation with small number of variables
using truth tables.
 Break large expressions into parts, as needed.
X+Z
0
1
0
1
1
1
1
1
(X+Y )(X+Z )
0
0
0
1
1
1
1
1
(X + Y ) = XY
XY
00
01
10
11
XY
1
0
0
0
(X + Y )
1
0
0
0

32. DeMorgan’s Law

33. DeMorgan’s Laws for n Variables
 We can extend DeMorgan’s laws to 3 variables by applying the laws
for two variables.
(X + Y + Z ) = (X + (Y + Z )) - by associative law
= X (Y + Z ) - by DeMorgan’s law
= X (Y Z ) - by DeMorgan’s law
= X YZ  - by associative law
(XYZ) = (X(YZ )) - by associative law
= X  + (YZ ) - by DeMorgan’s law
= X  + (Y  + Z ) - by DeMorgan’s law
= X  + Y  + Z  - by associative law
 Generalization to n variables.
– (X1 + X2 +    + Xn) = X 1X 2    X n
– (X1X2    Xn) = X 1 + X 2 +    + X n

34. Simplification of Boolean Expressions
F=X YZ +X YZ +XZ
X
Y
Z
X
Y
Z
X
Y
Z
by identity 14
F=X Y(Z +Z )+XZ
by identity 7
F=X Y1+XZ
=X Y +XZ by identity 2

35. The Duality Principle
 The dual of a Boolean expression is obtained by interchanging all
ANDs and ORs, and all 0s and 1s.
– example: the dual of A+(BC )+0 is A(B+C )1
 The duality principle states that if E1 and E2 are Boolean
expressions then
E1= E2  dual (E1)=dual (E2)
where dual(E) is the dual of E. For example,
A+(BC )+0 = (B C )+D  A(B+C)1 = (B +C )D
Consequently, the pairs of identities (1,2), (3,4), (5,6), (7,8),
(10,11), (12,13), (14,15) and (16,17) all follow from each other
through the duality principle.

36. The Consensus Theorem
Theorem. XY + X Z +YZ = XY + X Z
Proof. XY + X Z +YZ = XY + X Z + YZ(X + X ) 2,7
= XY + X Z + XYZ + X YZ 14
= XY + XYZ + X Z + X YZ 10
= XY(1 + Z ) + X Z(1 + Y ) 2,14
= XY + X Z 3,2
Example. (A + B )(A + C ) = AA + AC + AB + BC
= AC + AB + BC
= AC + AB
Dual. (X + Y )(X  + Z )(Y + Z ) = (X + Y )(X  + Z )

37. Taking the Complement of a Function
Method 1. Apply DeMorgan’s Theorem repeatedly.
(X(YZ + YZ )) = X  + (YZ + YZ )
= X + (YZ)(YZ )
= X + (Y + Z )(Y + Z)
Method 2. Complement literals and take dual
(X (YZ + YZ ))= dual(X(YZ + YZ))
= X + (Y + Z )(Y + Z)

38. Sum of Products Form
 The sum of products is one of two standard forms for Boolean
expressions.
sum-of-products-expression = term + term ... + term
term = literal  literal    literal
Example. X YZ + X Z + XY + XYZ
 A minterm is a term that contains every variable, in either
complemented or uncomplemented form.
Example. in expression above, X YZ is minterm, but X Z is not
 A sum of minterms expression is a sum of products expression in
which every term is a minterm
Example. X YZ + XYZ + XYZ  + XYZ is sum of minterms expression that is
equivalent to expression above

39. Product of Sums Form
 The product of sums is the second standard form for Boolean
expressions.
product-of-sums-expression = s-term  s-term ...  s-term
s-term = literal + literal +  + literal
Example. (X+Y+Z )(X+Z)(X+Y)(X+Y+Z)
 A maxterm is a sum term that contains every variable, in
complemented or uncomplemented form.
Example. in exp. above, X+Y+Z is a maxterm, but X+Z is not
 A product of maxterms expression is a product of sums expression in
which every term is a maxterm
Example. (X+Y+Z )(X+Y+Z)(X+Y+Z)(X+Y+Z) is product of maxterms
expression that is equivalent to expression above

40. NAND and NOR Gates
NAND Gate X
X
Y (XY) NOR Gate
(X+Y)
Y
 In certain technologies (including CMOS), a NAND (NOR) gate is
simpler & faster than an AND (OR) gate.
 Consequently circuits are often constructed using NANDs and NORs
directly, instead of ANDs and ORs.
 Alternative gate representations makes this easier.
= =
= =

41. Exclusive Or and Odd Function
A
AB 
+AB
B
 The odd function on n variables is 1 when an odd number of its
variables are 1.
– odd(X,Y,Z ) = XY Z + X Y Z  + X Y Z + X Y Z = X Y Z
– similarly for 4 or more variables
 Parity checking circuits use the odd function to provide a simple
integrity check to verify correctness of data.
– any erroneous single bit change will alter value of odd function, allowing
detection of the change
EXOR gate
Alternative Implementation
A
B
 The EXOR function is defined by AB = AB  + AB.

42. Positive and Negative Logic
 In positive logic systems, a high voltage is associated with a logic 1,
and a low voltage with a logic 0.
– positive logic is just one of two conventions that can be used to associate
a logic value with a voltage
– sometimes it is more convenient to use the opposite convention
 In logic diagrams that use negative logic, a polarity indicator is used
to indicate the correct logical interpretation for a signal.
X
Y XY X+Y
X
Y
 Circuits commonly use a combination of positive and negative logic.

43. Analysis example

44. Truth tables from logic diagram

45. Logic simulation

46. Decoder Fundamentals
 Route data to one specific output line.
 Selection of devices, resources
 Code conversions.
 Arbitrary switching functions
– implements the AND plane
 Asserts one-of-many signal; at most one output will be
asserted for any input combination

47. Encoding
Binary
Decimal Unencoded Encoded
0 0001 00
1 0010 01
2 0100 10
3 1000 11
Note: Finite state machines may be unencoded ("one-hot")
or binary encoded. If the all 0's state is used, then
one less bit is needed and it is called modified
one-hot coding.

48. Why Encode?
A Logarithmic Relationship
0 25 50 75 100 125 150
N
Log2(N)
8
7
6
5
4
3
2
1
0

49. 2:4 Decoder
1 1
1 0
0 1
00
D 0
D 1
A
B
A
B
A
B
A
B
AND 2
AND 2 A
AND 2 A
AND 2 B
Y
Y
Y
Y
E Q 3
E Q 2
E Q 1
E Q 0
What happens when the inputs goes from 01 to 10?

50. 2:4 Decoder with Enable
1 1
1 0
0 1
00
D 0
D 1
ENABLE
A
B
C
A
B
C
A
B
C
A
B
C
Y
Y
Y
Y
E Q 3
E Q 2
E Q 1
E Q 0
AND 3
AND 3 A
AND 3 A
AND 3 B

51. 2:1 Multiplexer
A
S
B
A
B
A
B
Y X1
Y X2
A
B
Y Y

52. Design synthesis procedure

53. Half Adder

54. Full Adder – with EXOR, AND and OR

55. Full Adder – with EXOR and NAND
 One-bit Full Adder (FA)
– 3 inputs: A, B, C
– 2 outputs: S, Co
– Truth table:
 Schematic View:
– cell-based approach
A, B, C S, Co
0, 0, 0 0, 0
0, 0, 1 1, 0
0, 1, 0 1, 0
0, 1, 1 0, 1
1, 0, 0 1, 0
1, 0, 1 0, 1
1, 1, 0 0, 1
1, 1, 1 1, 1
C S
B
A
Co

56. Ripple Carry Adder