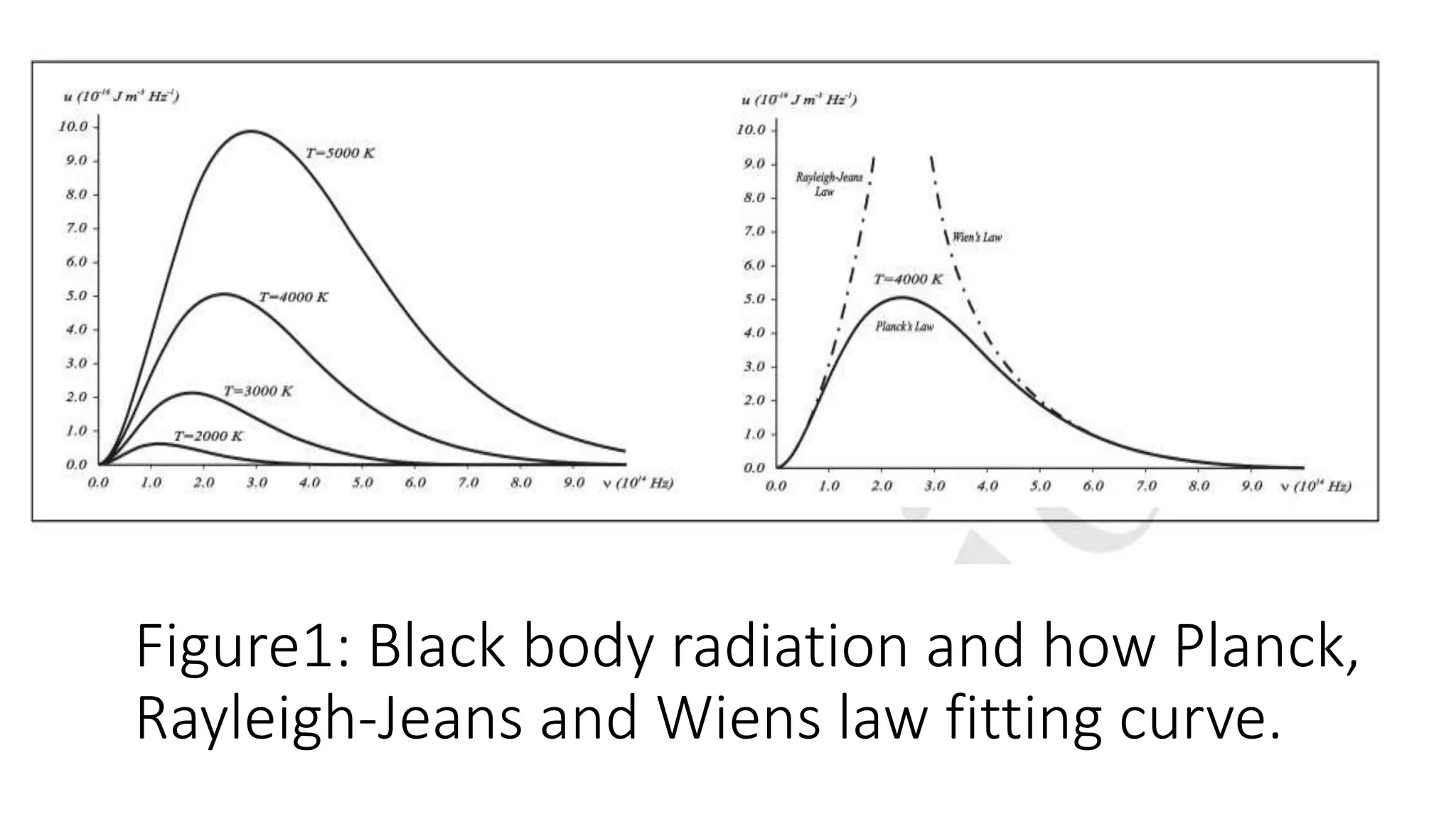
The document discusses the wave-particle duality of matter and radiation, highlighting key experiments and phenomena such as black body radiation, the photoelectric effect, and the Compton effect. It emphasizes that particles like electrons exhibit both wave-like and particle-like properties, challenging classical physics concepts. The document also details experiments such as the Davisson-Germer and double-slit experiments which demonstrate the interference patterns associated with particles.

1. Submitted by: Preeti Choudhary
Roll No: 21700304
chaudarypreeti1997@gmail.com

2. Contents
1. Particle properties of waves
• Blackbody radiation
• Photoelectric effect
• Compton effect
2. Wave properties of particles
• Davisson–Germer experiment
• Double slit experiment with particles

3. • According to classical physics, a particle is characterized by an energy
E and a momentum p, whereas a wave is characterized by an
amplitude and a wave vector k(|k| = 2π/λ) that specifies the direction
of propagation of the wave. Particles and waves exhibit entirely
different behaviours;
• These rigid concepts do not work in actual physical world. You have
often come across one Qs - ”Electrons are wave or particle?”. Well the
ans is electrons are like electrons. Sometimes a property of electron
matches with the classical concept of particle sometimes another
property matches with classical concept of a wave.
Particle Properties of waves

4. • If you heat a solid object, the object glows and emits thermal
radiation. As the temperature increases, the object becomes red,
then yellow, then white. The thermal radiation emitted by glowing
solid objects consists of a continuous distribution of frequencies
ranging from infrared to ultraviolet. The continuous pattern of the
distribution spectrum is in sharp contrast to the radiation emitted by
heated gases; the radiation emitted by gases has a discrete
distribution spectrum: a few bright and dark lines.
• J. Stefan found experimentally that the total power per unit surface
area radiated by a glowing object of temperature T is
P = σT4
Black body radiation

5. Figure1: Black body radiation and how Planck,
Rayleigh-Jeans and Wiens law fitting curve.

6. The photoelectric effect provides a direct confirmation for the energy quantization
of light. In electrons were observed to be ejected from metals when irradiated with
light with the following experimental observations.
(1) If the frequency of the incident radiation is smaller than the metal’s threshold
frequency— a frequency that depends on the properties of the metal—no electron
can be emitted regardless of the radiation’s intensity.
(2) No matter how low the intensity of the incident radiation, electrons will be
ejected instantly the moment the frequency of the radiation exceeds the threshold
frequency ν0
(3) At any frequency above ν0, the number of electrons ejected increases with the
intensity of the light but does not depend on the light’s frequency
(4) The kinetic energy of the ejected electrons depends on the frequency but not
on the intensity of the beam; the kinetic energy of the ejected electron increases
linearly with the incident frequency.
Photoelectric effect

7. • Compton found that when X-rays are make incident on free electrons, the
wavelength of the scattered radiation is larger than the wavelength of the
incident radiation. How do we explain it? According to classical physics, the
incident and scattered radiation should have the same wavelength. since
the energy of the X-ray radiation is too high to be absorbed by a free
electron, the incident X-ray would then provide an oscillatory electric field
which sets the electron into oscillatory motion, hence making it radiate
light with the same wavelength
• The experimental findings of Compton reveal that the wavelength of the
scattered X-radiation increases by an amount ∆λ, called the wavelength
shift, and that ∆λ depends not on the intensity of the incident radiation,
but only on the scattering angle. Compton scattering formula
∆λ = λ’ − λ = h /mec (1 − cos θ) = 2λC (sin2 θ /2)
Compton effect

8. • As discussed above—in the black body radiation photoelectric effect,
and the Compton effect —radiation exhibits particle-like
characteristics in addition to its wave nature.
• de Broglie took things even further by suggesting that this wave–
particle duality is not restricted to radiation, but must be universal: all
material particles should also display a dual wave–particle behaviour.
That is, the wave–particle duality present in light must also occur in
matter.
• Each material particle of momentum p behaves as a group of waves
(matter waves) whose wavelength λ and wave vector k are governed
by the speed and mass of the particle λ = h /p
Wave properties of particle

9. • This is actually the electron diffraction experiment from the crystal.
Electrons strike the crystal’s surface at an angle φ ; the detector,
symmetrically located from the electron source, measures the
number of electrons scattered at an angle θ, where θ is the angle
between the incident and scattered electron beams.
• The results follows the Brag reflection pattern - nλ = 2d sin φ
Davisson–Germer experiment

10. • If you do a double slit experiment with the particles, you will get the
interference pattern which was explained initially by saying that the
particles are de Broglie waves with a wavelength so they mutually interfere
and produces interference pattern.
• But if you do the experiment by throwing one particle at a time then you
also get the interference pattern. How and with whom the the particle (de
Broglie wave) interfere when it is the only particle which is on move? This
is again one of the core question of quantum mechanics, and our current
understanding is - the particle interfere with itself. The particle do not
passes through one hole until you particularly measure the motion and
find thorough which slit the particle is passing. In brief, the particle passes
through every possible paths.
Double slit experiment with particles

11. Thank you
