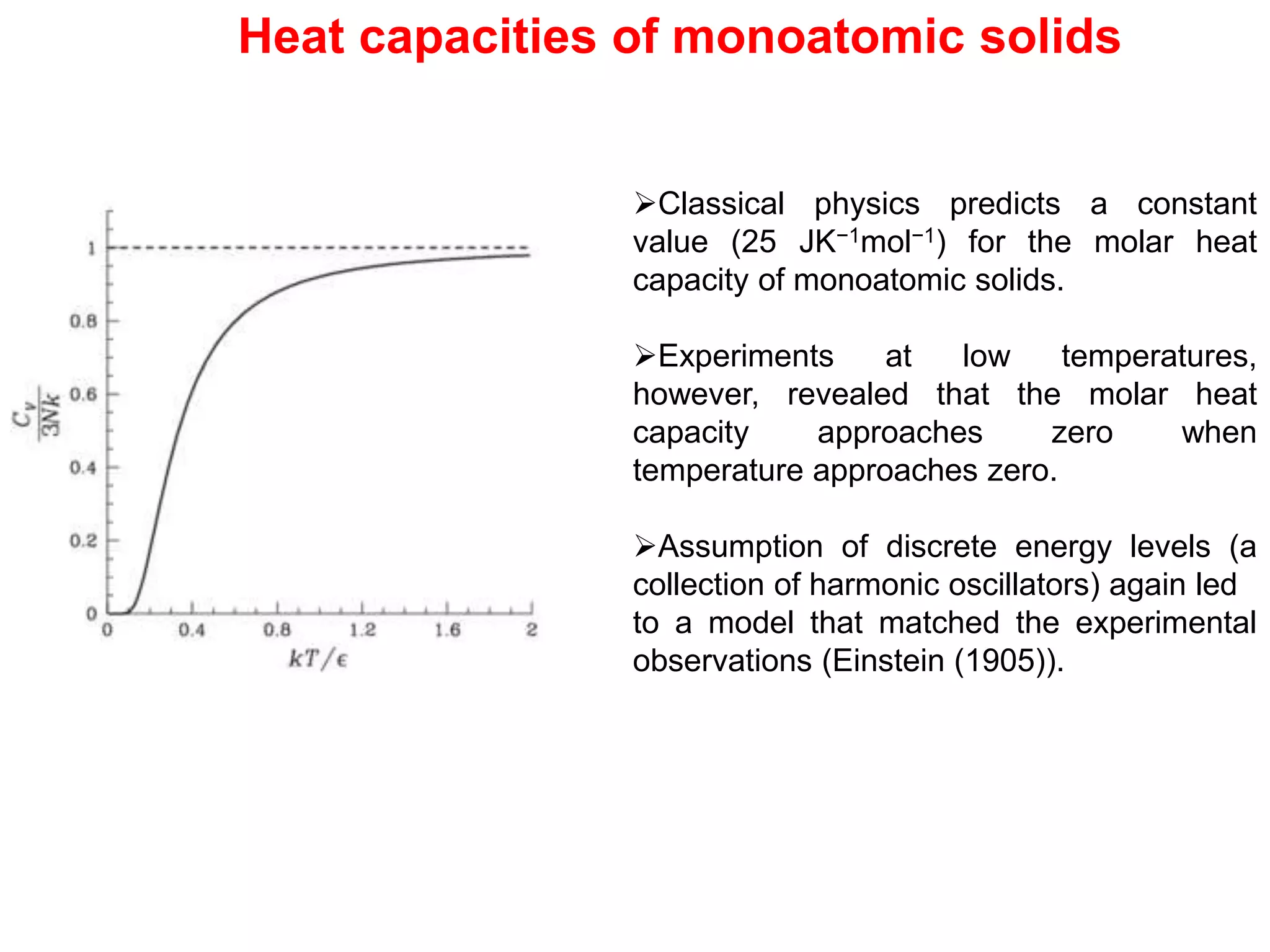
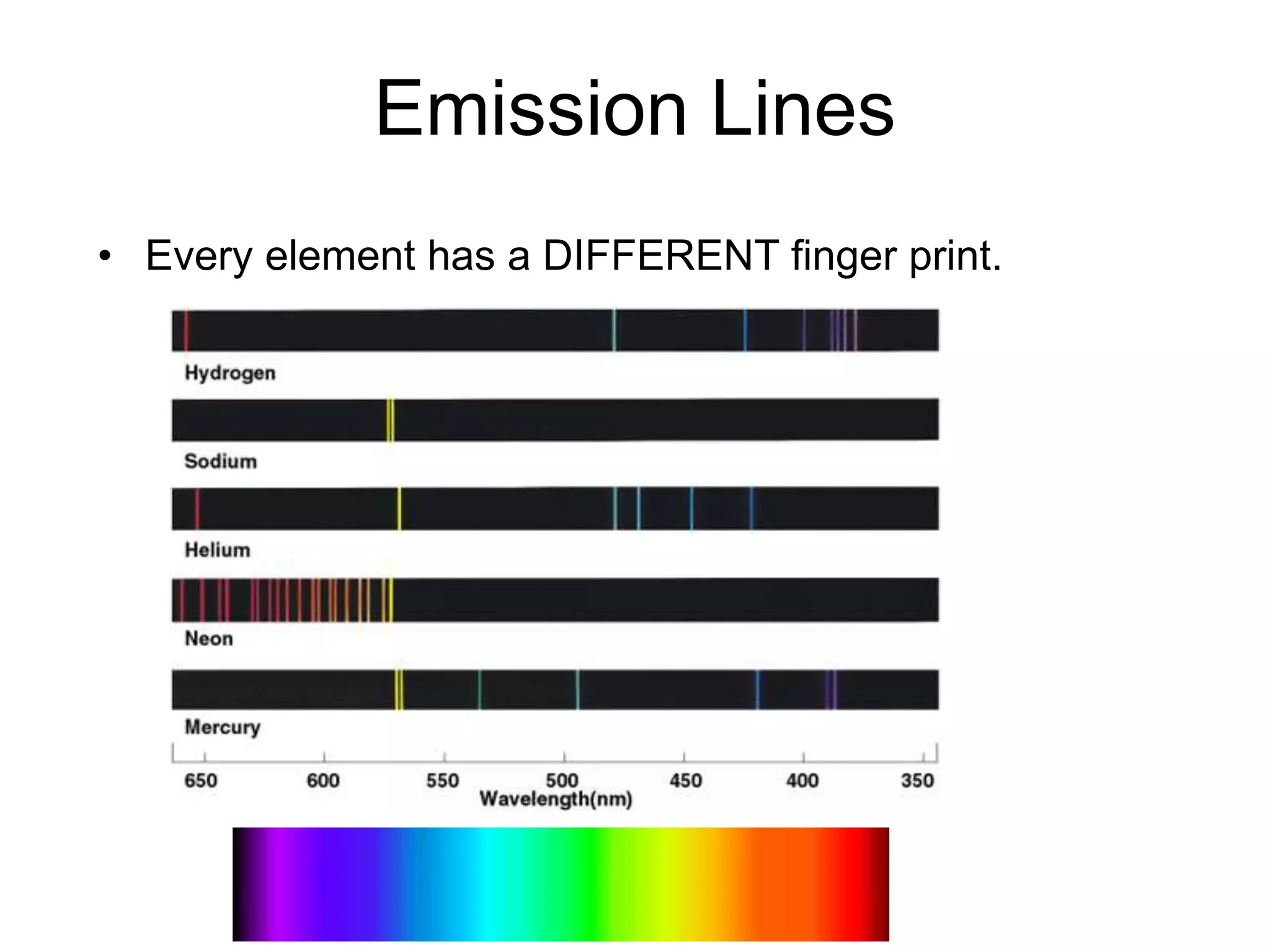
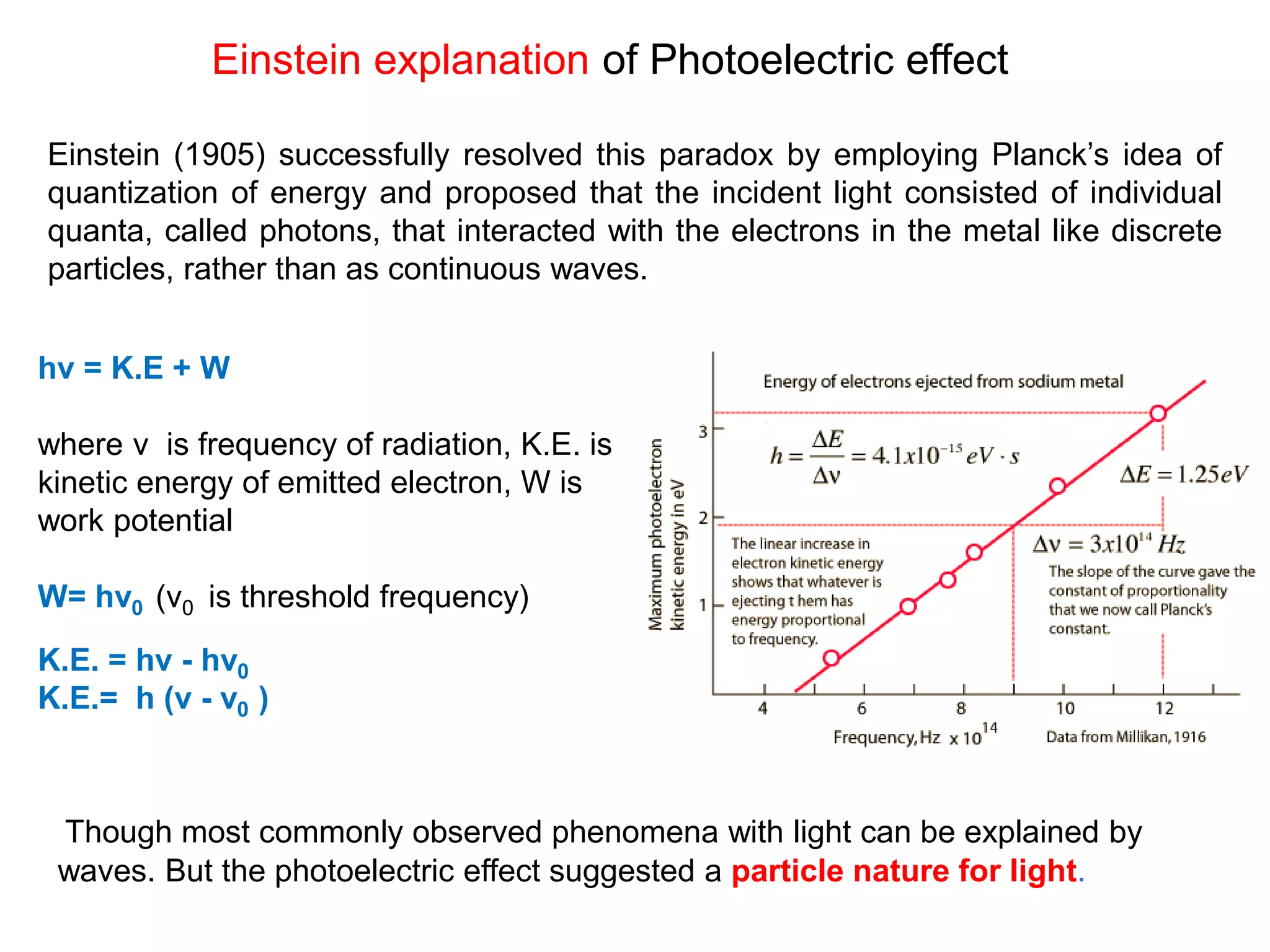
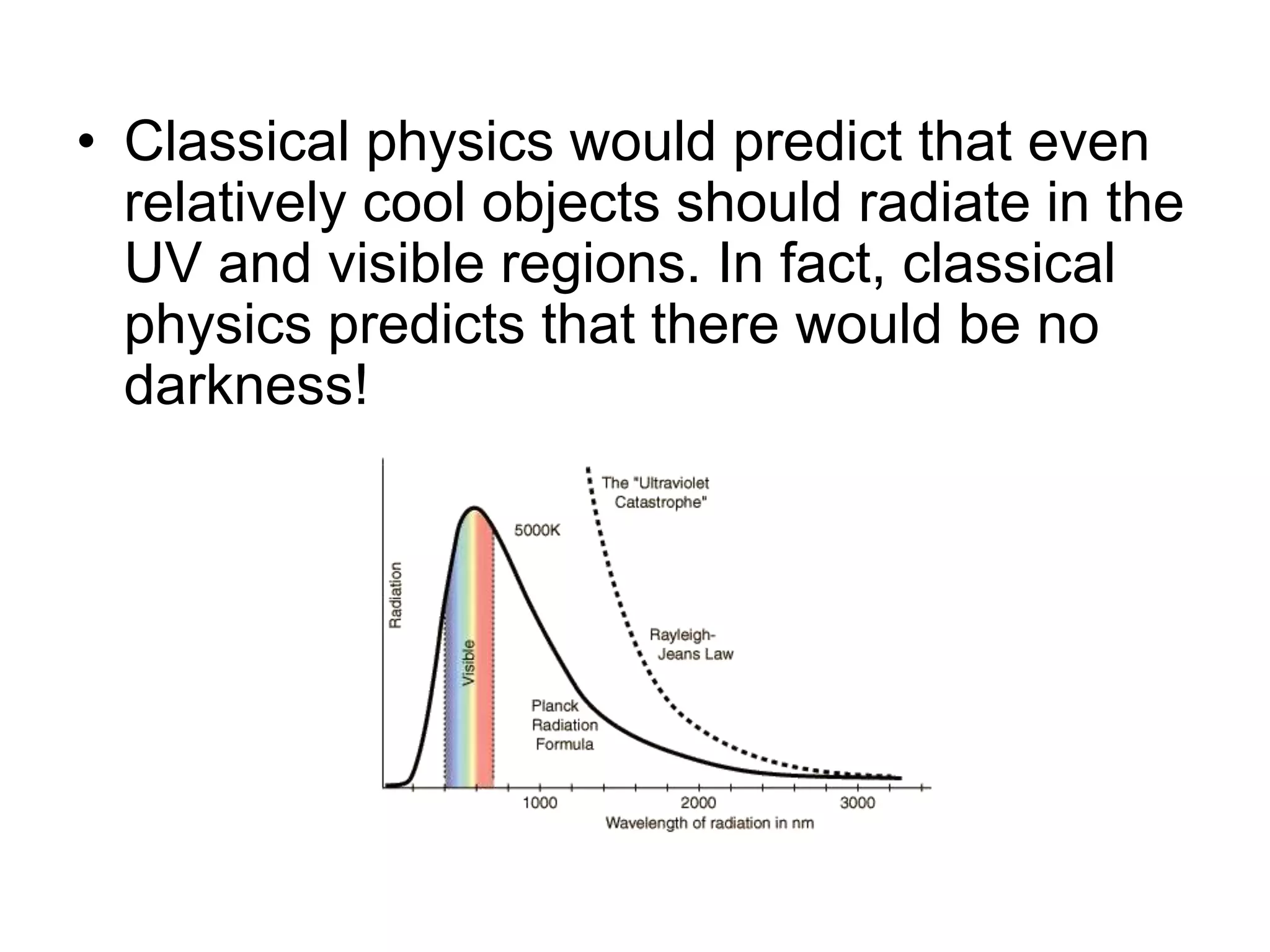
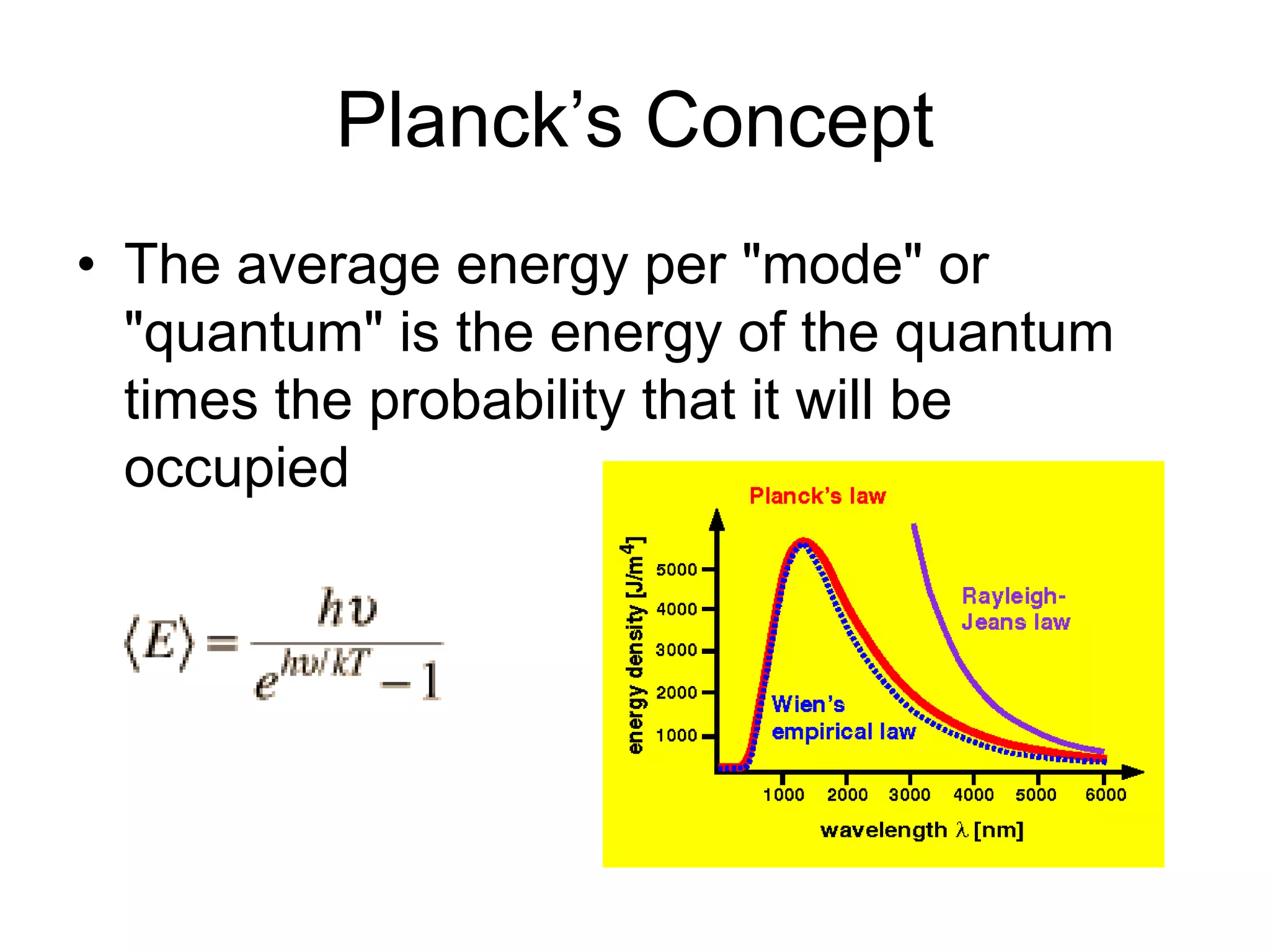
- Classical mechanics fails to fully describe phenomena at the atomic scale such as blackbody radiation, heat capacities of solids at low temperatures, and the photoelectric effect. This led to the development of quantum mechanics. - Planck explained blackbody radiation by proposing that electromagnetic radiation is emitted and absorbed in discrete 'quanta' with energy proportional to frequency. This ended the "ultraviolet catastrophe" of classical physics. 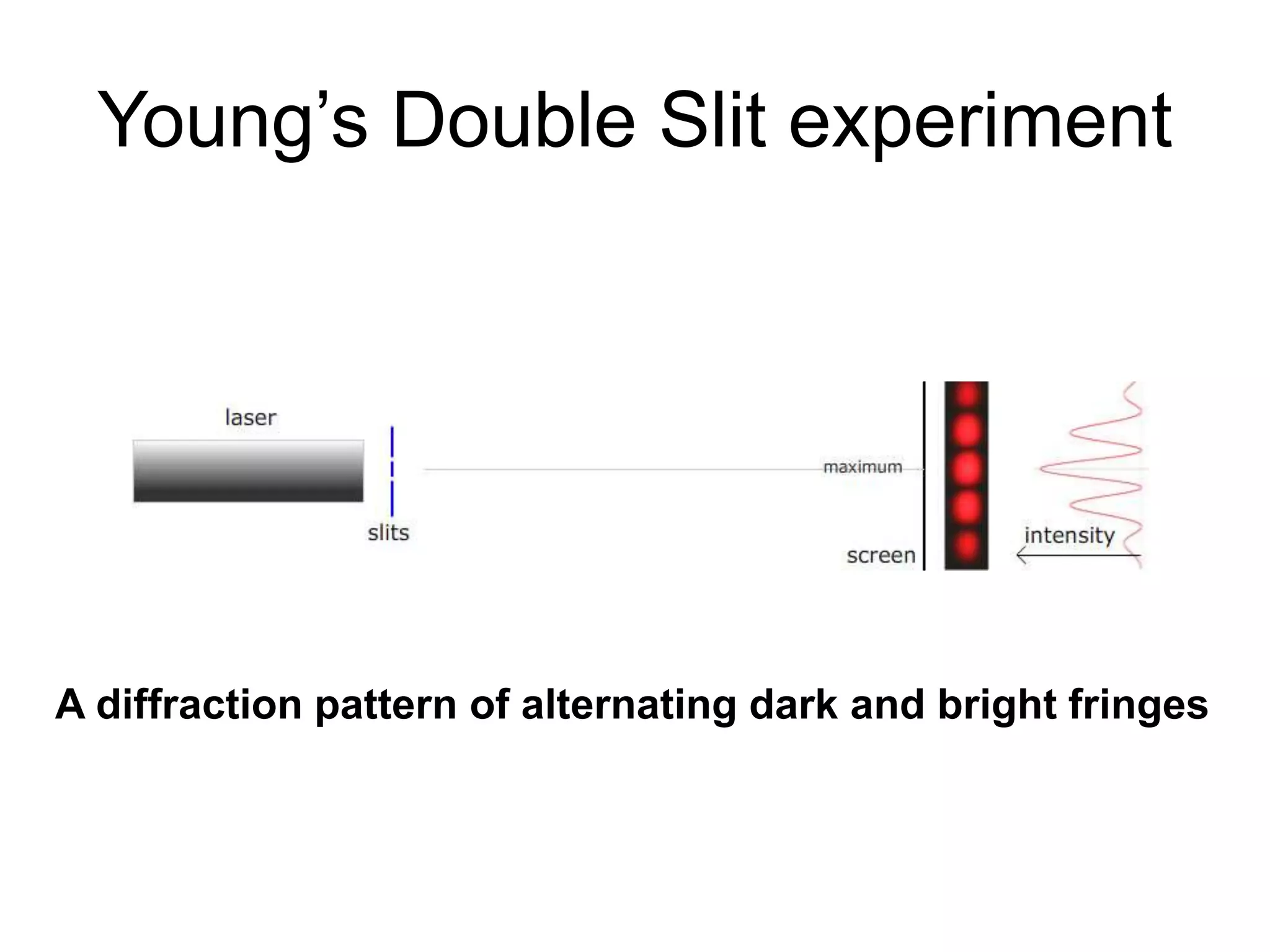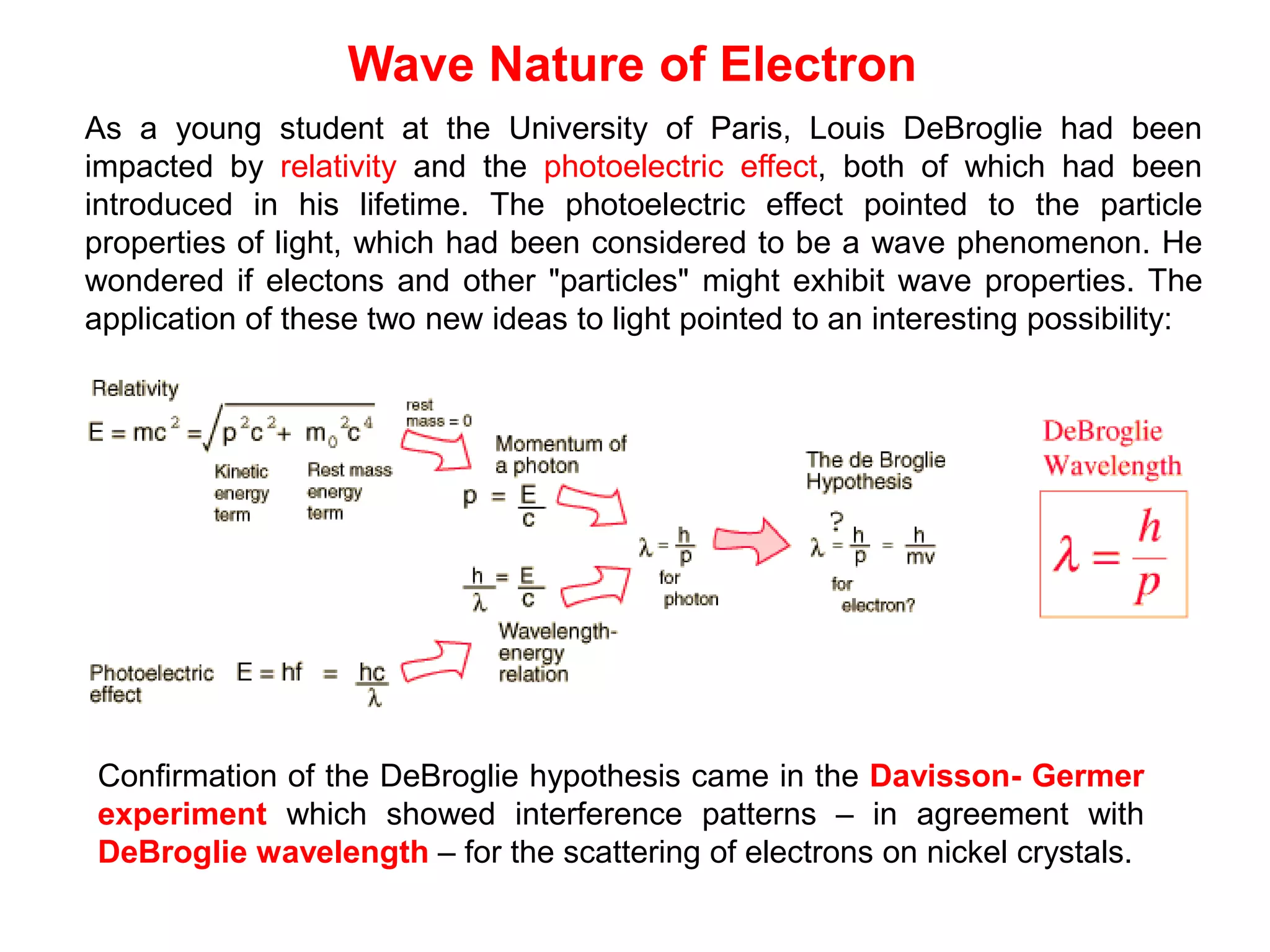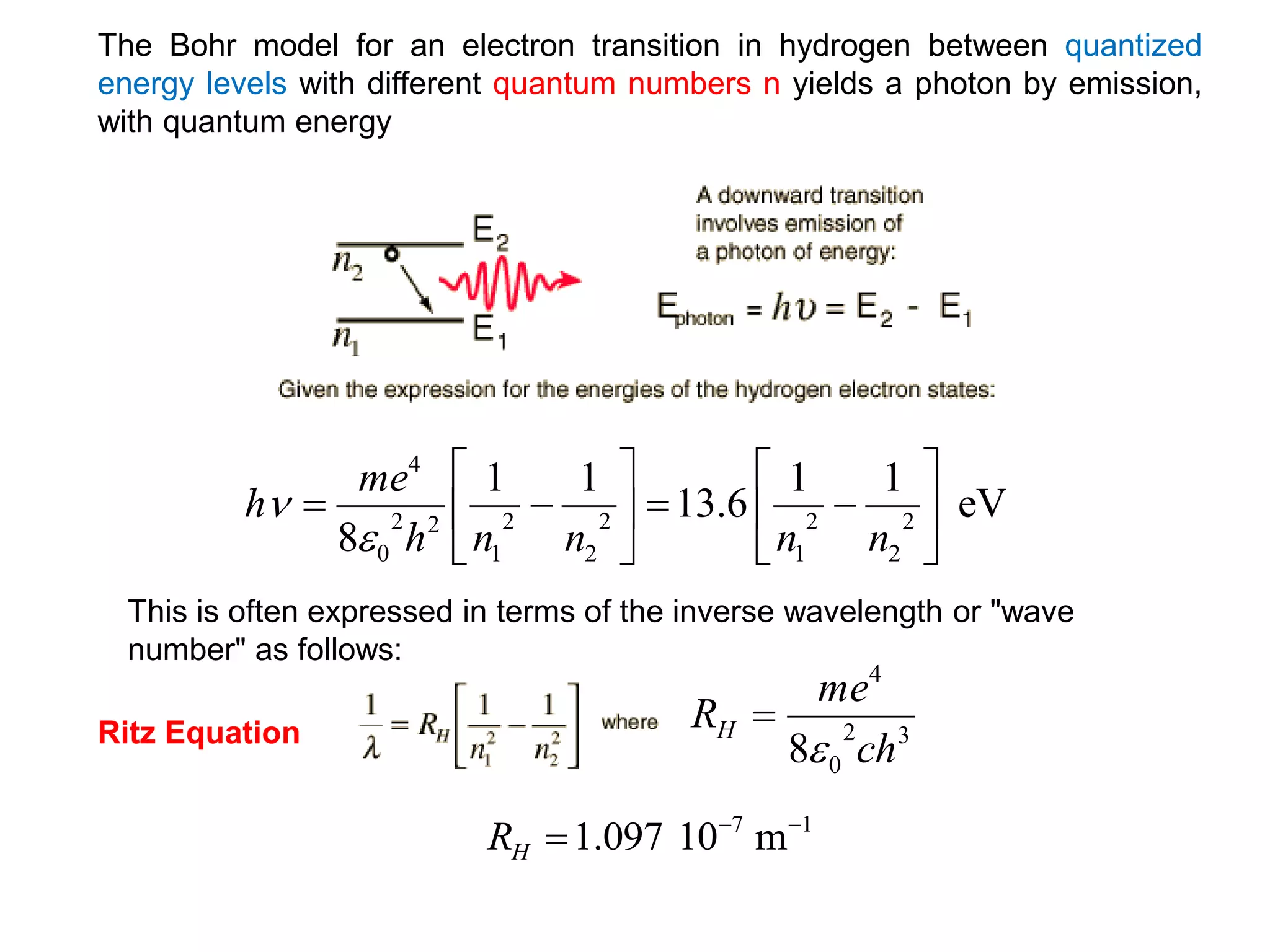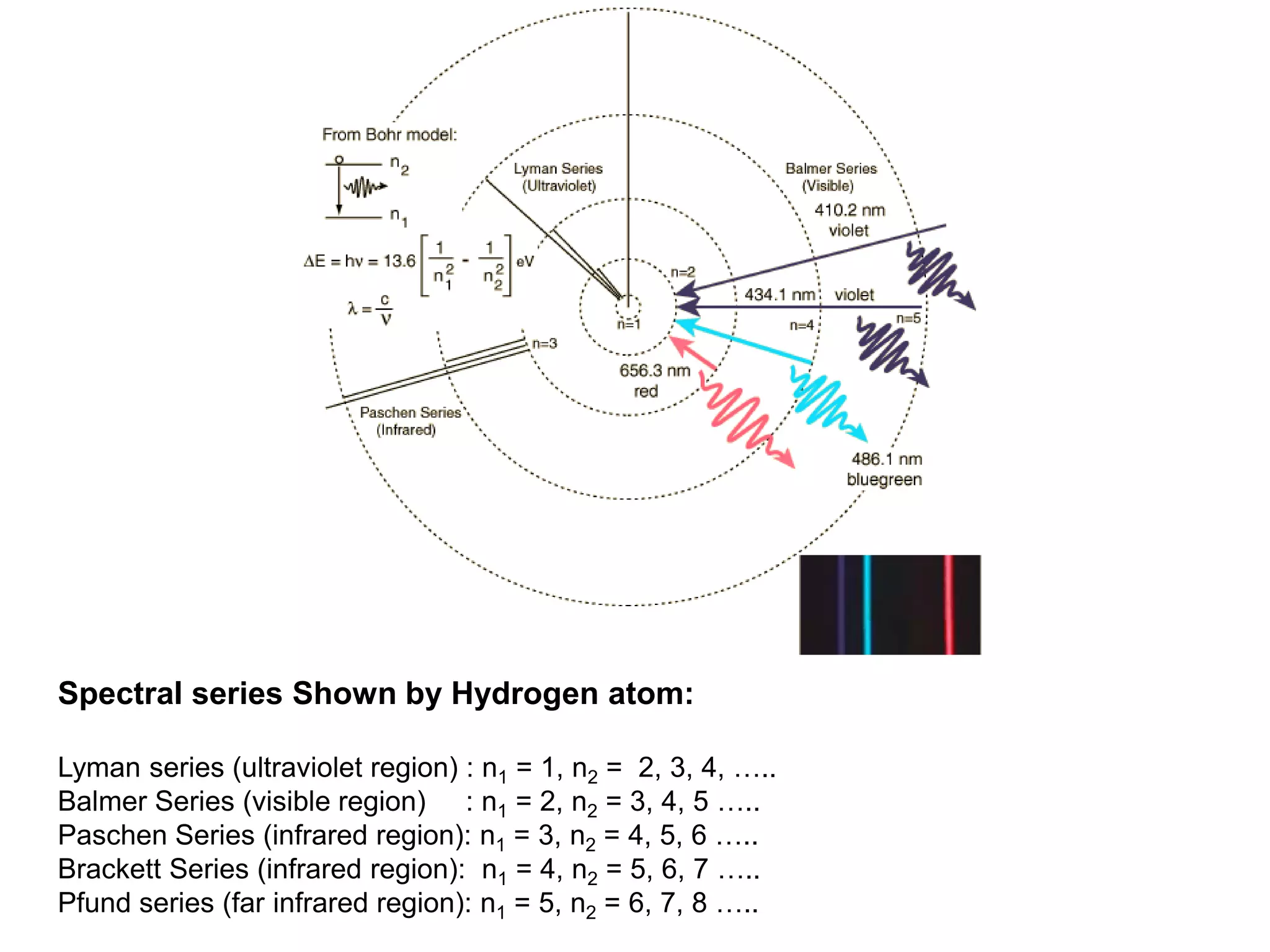- De Broglie associated waves with all particles, suggesting light has both wave-like and particle-like properties. This was confirmed through experiments and led to the modern concept of wave-particle duality.

1. Degree of Freedom
• Number of independent intensive variables
needed to specify its intensive state.
T, P and mole fraction in each phase.

2. What happens to boiling point or freezing
point of a liquid in the presence of a solute?
What happens to chemical potential of a liquid in the
presence of solute?
sol
ute.
vol
ati
l
e
-
non
of
addi
ti
on
on
decreases
l
i
qui
d
a
of
potenti
al
Chem
i
cal
)
l
aw
s
(Raoul
t'
l
n
l
n
l
n
(g)
(l
)
sol
ute
a
of
presence
In
l
n
(g)
(l
)
sol
vent
pure
For
*




















A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
x
p
p
x
RT
p
p
RT
p
RT
p
RT












3. There is elevation of boiling point upon addition of
a solute.
There is depression of freezing point upon addition of
a solute.

4. Ice-NaCl phase diagram

5. Pre- Quantum Mechanics
(History of quantum mechanics)
Laws of motion formulated by Galileo, Newton, Lagrange, Hamilton, Maxwell which
preceded quantum theory are referred to as Classical Mechanics.
•The essence of classical mechanics is given in Newton’s laws
•For a given force if the initial position and the velocity of the particle is known all
physical quantities such as position, momentum, angular momentum, energy etc. at
all subsequent times can be calculated.
Other formulations provide same information as obtained from Newton’s
Formulation.
Failures of Classical mechanics led to the Need of Quantum mechanics.
F
dt
r
d
m 
2
2 

6. Why are Cherries Red and
Blueberries blue ?
A fundamentally new understanding of size
is required ?

7. Why CO2 is a greenhouse gas ?
How electricity can move through
metals ?

8. • Classical mechanics describes the motion
of a baseball, the spinning of a top, and
the flight of an airplane.
• Quantum mechanics describes the motion
of electrons and the shapes of molecules
such as trans fats, as well as electrical
conductivity and superconductivity.

9. Classical mechanics failed to describe
experiments on atomic and molecular
phenomena :
1. classical physics cannot describe light
particles (for example, electrons)
2. a new theory is required (i.e., quantum
mechanics)
Recall that classical physics:
1. allows energy to have any desired value
2. predicts a precise trajectory for particles
(i.e., deterministic)

10. Quantization of Energy

11. Failures of Classical mechanics
Black Body Radiation:
WHAT IS BLACK BODY ?
A black body is a theoretical object that absorbs 100% of the radiation that
hits it. Therefore it reflects no radiation and appears perfectly black.
It is also a perfect emitter of radiation. At a particular temperature the black
body would emit the maximum amount of energy possible for that temperature.

12. An opaque object emits electromagnetic radiation
according to its temperature

13. • Red stars are relatively cool. A yellow star,
such as our own sun, is hotter. A blue star
is very hot.

14. Planck Spectrum
• As an object is heated,
the radiation it emits
peaks at higher and
higher frequencies.
• Shown here are curves
corresponding to
temperatures of
300 K (room temperature),
1000 K (begin to glow deep
red)
4000 K (red hot), and
7000 K (white hot).

15. Rayleigh-Jean’s law
• The energy density pν per unit
frequency interval at a frequency ν is,
according to the The Rayleigh-Jeans
Radiation,
kT
E
E
c
v




 3
2
8


16. Black body
Radiation
• Although the
Rayleigh-Jeans law
works for low
frequencies, it
diverges at high ν
• This divergence for
high frequencies is
called the ultraviolet
catastrophe.

17. • Classical physics would predict that even
relatively cool objects should radiate in the
UV and visible regions. In fact, classical
physics predicts that there would be no
darkness!

18. Black body Radiation
• Max Planck explained the blackbody
radiation in 1900 by assuming that the
energies of the oscillations of electrons
which gave rise to the radiation must be
proportional to integral multiples of the
frequency, i.e., E = nhν

19. Planck’s Concept
• The average energy per "mode" or
"quantum" is the energy of the quantum
times the probability that it will be
occupied

20. • Planck won the Nobel Prize in Physics in
1918
The recognition that energy changes in discreet
quanta at the atomic level marked the beginning of
quantum mechanics.

21. Classical physics predicts a constant
value (25 JK−1mol−1) for the molar heat
capacity of monoatomic solids.
Experiments at low temperatures,
however, revealed that the molar heat
capacity approaches zero when
temperature approaches zero.
Assumption of discrete energy levels (a
collection of harmonic oscillators) again led
to a model that matched the experimental
observations (Einstein (1905)).
Heat capacities of monoatomic solids

22. Atomic and molecular spectra
• Atomic and molecular spectra: Absorption
and emission of electromagnetic radiation
(i.e., photons) by atoms and molecules
occur only at discrete energy values.
• Classical physics would predict absorption
or emission at all energies.

23. Emission Lines
• Every element has a DIFFERENT finger print.

24. Wave or particle ??

25. Young’s Double Slit experiment
A diffraction pattern of alternating dark and bright fringes

26. Young Double Slit Experiment
(Wave Nature of Light)
The interference pattern would arise
only if we consider electrons as waves,
which interfere with each other (i.e.
constructive and deconstructive
interference).

27. Wave nature of photon (De Broglie)
• Particles such as
electrons has a wave
description.
p
h



28. De Broglie wave
• The de Broglie wave
for a particle is made
up of a superposition
of an infinitely large
number of waves of
form
  






 t
x
A
t
x 


 2
sin
,
The waves that are added together have
infinitesimally different wavelengths. This
superposition of waves produces a wave
packet.

29. RED LIGHT EJECTS SLOWER
ELECTRONS THAN BLUE
LIGHT

30. Photoelectric effect
• For a particular metal and a given color of light, say blue,
it is found that the electrons come out with a well-defined
speed, and that the number of electrons that come out
depends on the intensity of the light.
• If the intensity of light is increased, more electrons come
out, but each electron has the same speed, independent
of the intensity of the light.
• If the color of light is changed to red, the electron speed
is slower, and if the color is made redder and redder, the
electrons’ speed is slower and slower.
• For red enough light, electrons cease to come out of the
metal.

31. Failure of classical theory to explain Photoelectric effect
Using the classical Maxwell wave theory of light,
 the more intense the incident light the greater the energy with which the
electrons should be ejected from the metal. That is, the average energy carried by an
ejected (photoelectric) electron should increase with the intensity of the incident light.
Hence it is expected : lag time between exposure of the metal and emission of
electron.
Therefore, classical theory could not explain the characteristics of
photoelectric effect:
Instantaneous emission of electrons
Existence of threshold frequency
Dependence of kinetic energy of the emitted electron on the frequency of light.

32. Einstein explanation of Photoelectric effect
Einstein (1905) successfully resolved this paradox by employing Planck’s idea of
quantization of energy and proposed that the incident light consisted of individual
quanta, called photons, that interacted with the electrons in the metal like discrete
particles, rather than as continuous waves.
Though most commonly observed phenomena with light can be explained by
waves. But the photoelectric effect suggested a particle nature for light.
hν = K.E + W
where ν is frequency of radiation, K.E. is
kinetic energy of emitted electron, W is
work potential
W= hν0 (ν0 is threshold frequency)
K.E. = hν - hν0
K.E.= h (ν - ν0 )

33. Does light consist of particles or waves? When one focuses upon the different
types of phenomena observed with light, a strong case can be built for a wave
picture:
Phenomenon
Can be explained in terms of
waves.
Can be explained in terms of
particles.
Most commonly observed phenomena with light can be explained by waves.
But the photoelectric effect and the Compton scatering suggested a particle
nature for light. Then electrons too were found to exhibit dual natures.
Wave-Particle Duality: Light
Reflection
Refraction
Interference
Diffraction
Polarization
Photoelectric effect
Compton scattering

34. As a young student at the University of Paris, Louis DeBroglie had been
impacted by relativity and the photoelectric effect, both of which had been
introduced in his lifetime. The photoelectric effect pointed to the particle
properties of light, which had been considered to be a wave phenomenon. He
wondered if electons and other "particles" might exhibit wave properties. The
application of these two new ideas to light pointed to an interesting possibility:
Confirmation of the DeBroglie hypothesis came in the Davisson- Germer
experiment which showed interference patterns – in agreement with
DeBroglie wavelength – for the scattering of electrons on nickel crystals.
Wave Nature of Electron

35. DeBroglie Wavelengths
The de Broglie wavelength λ for macroscopic particles are negligibly small
This effect is extremely important for light particles, like electrons.

36. Wave or Particle (Size ??)
• Objects that are large in the absolute
sense have the property that the
wavelengths associated with them are
completely negligible compared to their
size. Therefore, large particles only
manifest their particle nature, they never
manifest their wave nature.

37. Quantization of angular
momentum
Bohr’s postulate

38. Bohr Atomic Model : Angular Momentum Quantization
 Bohr proposed a quantum restriction on classical model i.e. the angular
momentum of the revolving electron is an integral multiple of basic unit
(h/2π)
mvr = n (h/2π)
Combining the energy of the classical electron orbit with the quantization of
angular momentum, the Bohr approach yields expressions for the electron
orbit radii and energies:
substitution for r gives the Bohr energies and radii:

39. The Bohr model for an electron transition in hydrogen between quantized
energy levels with different quantum numbers n yields a photon by emission,
with quantum energy
This is often expressed in terms of the inverse wavelength or "wave
number" as follows:
eV
1
1
6
.
13
1
1
8
2
2
2
1
2
2
2
1
2
2
0
4
















n
n
n
n
h
me
h


3
2
0
4
8 ch
me
RH


1
7
m
10
097
.
1 


H
R
Ritz Equation

40. Spectral series Shown by Hydrogen atom:
Lyman series (ultraviolet region) : n1 = 1, n2 = 2, 3, 4, …..
Balmer Series (visible region) : n1 = 2, n2 = 3, 4, 5 …..
Paschen Series (infrared region): n1 = 3, n2 = 4, 5, 6 …..
Brackett Series (infrared region): n1 = 4, n2 = 5, 6, 7 …..
Pfund series (far infrared region): n1 = 5, n2 = 6, 7, 8 …..

41. Wave-particle duality
and Heisenberg Uncertainty
Principle
Can the radius be specified
exactly ?

49. • Although de Broglie’s equation justifies Bohr’s
quantization assumption, it also demonstrates a
deficiency of Bohr’s model. Heisenberg showed that the
waveparticle duality leads to the famous uncertainty
principle ∆x∆p ≈ h (9)
• One result of the uncertainty principle is that if the orbital
radius of an electron in an atom r is known exactly, then
the angular momentum must be completely unknown.
The problem with Bohr’s model is that it specifies r
exactly and it also specifies that the orbital angular
momentum must be an integral multiple of h¯. Thus the
stage was set for a new quantum theory which was
consistent with the uncertainty principle.

50. • Ru and Cs discovered by spectral analysis
(Bunsen and Kirchoff (1859-1863)
• Prediction of existence and properties of
Sc, Ga, and Ge (Mendeleev, 1869/1870)

51. Wavefunction
• The wave that in quantum mechanics
replaces the classical concept of particle
trajectory is called a wavefunction, ψ
(“psi”).

52. Wave equation for the harmonic motion
 
 
)
(
)
(
)
(
8
]
2
[
]
2
[
2
2
1
)
(
)
(
4
)
(
2
)
(
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
2
2
x
V
E
dx
x
d
m
h
V
E
m
h
p
h
V
E
m
p
V
m
p
V
mv
E
x
dx
x
d
x
dx
x
d



















































53. Operator
• A rule that transforms a given function into
another function