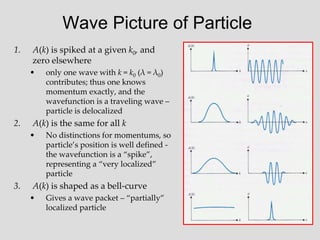
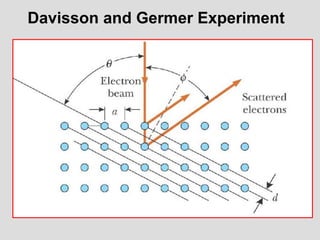
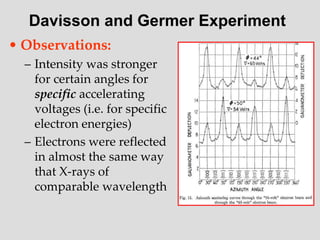
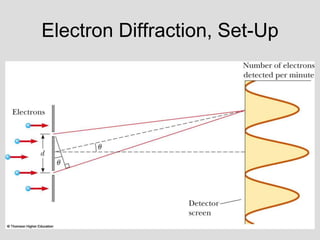
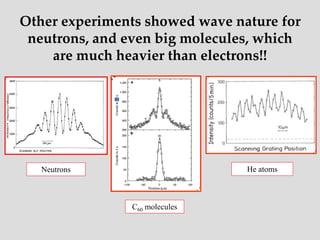
- Louis de Broglie hypothesized that all matter exhibits both wave and particle properties, with a wavelength inversely proportional to momentum, just as light does. - Experiments observing diffraction and interference of electrons, neutrons, atoms and molecules provided evidence that matter has wave-like properties consistent with a de Broglie wavelength, demonstrating the wave-particle duality of all matter. - The principle of complementarity states that matter and light cannot be fully described as either purely waves or particles, as the two models complement each other and neither is complete. Observing one property precludes observation of the other.

1. Wave Properties of Particles
Serway/Jewett chapters 38.5; 40.4 – 40.7

2. Photons and Waves Revisited
• Some experiments are best explained by
the photon model
• Some are best explained by the wave
model
• We must accept both models and admit that
the true nature of light is not describable in
terms of any single classical model
• The particle and wave models complement
one another

3. Dual Nature of EM radiation
• To explain all experiments with EM radiation
(light), one must assume that light can be
described both as wave (Interference, Diffraction)
and particles (Photoelectric Effect, Frank-Hertz
Experiment, x-ray production, x-ray scattering
from electron)
• To observe wave properties must make
observations using devices with dimensions
comparable to the wavelength.
– For instance, wave properties of X-rays were observed
in diffraction from arrays of atoms in solids spaced by a
few Angstroms

4. Louis de Broglie
• 1892 – 1987
• French physicist
• Originally studied
history
• Was awarded the
Nobel Prize in 1929
for his prediction of
the wave nature of
electrons

5. De Broglie’s Hypothesis
• Louis de Broglie postulated that the dual
nature of the light must be “expanded” to
ALL matter
– In other words, all material particles possess
wave-like properties, characterized by the
wavelength, λB, related to the momentum p of
the particle in the same way as for light
p
h
B 

de Broglie
wavelength of the
particle
Planck’s Constant
Momentum of the
particle

6. Wave Properties of Particles
• Louis de Broglie postulated that because photons have
both wave and particle characteristics, so too all forms of
matter have both properties
• For photons:
•
• De Broglie hypothesized that particles of well defined
momentum also have a wavelength, as given above, the
de Broglie wavelength
p
h
Or
h
c
h
c
E
p
h
E









,

7. Frequency of a Particle
• In an analogy with photons, de Broglie
postulated that a particle would also have a
frequency associated with it
• These equations present the dual nature of
matter
– Particle nature, p and E
– Wave nature, λ and ƒ ( and k)







 f
h
hf
E
h
E
f 2
2

8. De Broglie’s Hypothesis
• De Broglie’s waves are not EM waves
– He called them “pilot” or “material” waves
– λB depends on the momentum and not on
physical size of the particle
• For a non-relativistic free particle:
– Momentum is p = mv, here v is the speed of the particle
– For free particle total energy, E, is kinetic energy
Em
h
mv
h
p
h
B
2




2
2
2
2
mv
m
p
K
E 



9. Photons and Waves Revisited
• Some experiments are best explained by
the photon model
• Some are best explained by the wave
model
• We must accept both models and admit
that the true nature of light is not
describable in terms of any single classical
model
• Also, the particle model and the wave
model of light complement each other

10. Complementarity
• The principle of complementarity states
that the wave and particle models of either
matter or radiation complement each other
• Neither model can be used exclusively to
describe matter or radiation adequately
• No measurements can simultaneously
reveal the particle and the wave properties
of matter

11. The Principle of Complementarity
and the Bohr Atom
• How can we understand electron orbits in
hydrogen atom from wave nature of the electron?
• Remember: An electron can take only certain
orbits: those for which the angular momentum, L,
takes on discrete values
• How does this relate to the electron’s de
Broglie’s wavelength?

n
mvr
L 


12. The Principle of Complementarity
• Only those orbits are allowed,
which can “fit” an integer
(discrete) number of the electron’s
de Broglie’s wavelength
• Thus, one can “replace” 3rd Bohr’s
postulate with the postulate
demanding that the allowed orbits
“fit” an integer number of the
electron’s de Broglie’s wavelength
• This is analogous to the standing
wave condition for modes in
musical instruments
B
B
B
B
B
n
r
n
h
n
r
h
mv
mv
h
p
h
n
mvr
L















2
2


B
n
r 
 
2

13. •De Broglie’s Hypothesis predicts
that one should see diffraction
and interference of matter waves
•For example we should observe
–Electron diffraction
–Atom or molecule diffraction

14. Estimates for De Broglie wavelength
• Bullet:
– m = 0.1 kg; v = 1000 m/s  λB ~ 6.63×10-36 m
• Electron at 4.9 V potential:
– m = 9.11×10-31 kg;
– E~4.9 eV  λB ~ 5.5×10-10 m = 5.5 Å
• Nitrogen Molecule at Room Temperature:
– m ~ 4.2×10-26 kg;
– E = (3/2)kBT  0.0375 eV  λB ~2.8×10-11 m = 0.28 Å
• Rubidium (87) atom at 50 nK:
– λB ~ 1.2×10-6 m = 1.2 mm = 1200 Å
mE
h
mv
h
p
h
B
2





15. Diffraction of X-Rays by Crystals
• X-rays are electromagnetic waves of relatively short
wavelength (λ = 10-8 to 10-12 m = 100 – 0.01 Å)
• Max von Laue suggested that the regular array of
atoms in a crystal (spacing in order of several
Angstroms) could act as a three-dimensional
diffraction grating for x-rays

16. X-ray Diffraction Pattern

17. X-Ray Diffraction
• This is a two-dimensional
description of the
reflection (diffraction) of
the x-ray beams
• The condition for
constructive interference is
where n = 1, 2, 3

 n
d 
sin
2
• This condition is
known as Bragg’s law
• This can also be used
to calculate the spacing
between atomic planes

18. Davisson-Germer Experiment
• If particles have a wave nature, then under
appropriate conditions, they should exhibit
diffraction
• Davisson and Germer measured the
wavelength of electrons
• This provided experimental confirmation of
the matter waves proposed by de Broglie

19. Davisson and Germer Experiment
• Electrons were directed
onto nickel crystals
• Accelerating voltage is
used to control electron
energy: E = |e|V
• The scattering angle
and intensity (electron
current) are detected
– φ is the scattering angle

20. Davisson and Germer Experiment
• If electrons are “just” particles, we expect a smooth
monotonic dependence of scattered intensity on
angle and voltage because only elastic collisions are
involved
• Diffraction pattern similar to X-rays would be
observed if electrons behave as waves

21. Davisson and Germer Experiment

22. Davisson and Germer Experiment
• Observations:
– Intensity was stronger
for certain angles for
specific accelerating
voltages (i.e. for specific
electron energies)
– Electrons were reflected
in almost the same way
that X-rays of
comparable wavelength

23. Davisson and Germer Experiment
• Observations:
– Current vs accelerating
voltage has a maximum,
i.e. the highest number
of electrons is scattered
in a specific direction
– This can’t be explained
by particle-like nature of
electrons  electrons
scattered on crystals
behave as waves
For φ ~ 50° the maximum is at ~54V

24. Davisson and Germer Experiment
• For X-ray Diffraction on Nickel


50
65
A
65
.
1
;
A
91
.
0
sin
2
o
ray
-
X
o
111














d
d

25. Davisson and Germer Experiment
• (Problem 40.38) Assuming the wave nature
of electrons we can use de Broglie’s
approach to calculate wavelengths of a
matter wave corresponding to electrons in
this experiment
• V = 54 V  E = 54 eV = 8.64×10-18J

A
67
.
1
J
10
6
.
8
kg
10
1
.
9
2
sec
-
J
10
63
.
6
2
,
2
,
2
18
31
34
2













B
B
mE
h
mE
p
m
p
E


This is in excellent agreement with wavelengths of
X-rays diffracted from Nickel!

26. • In previous experiments many electrons
were diffracted
• Will one get the same result for a single
electron?
• Such experiment was performed in 1949
– Intensity of the electron beam was so low that
only one electron at a time “collided” with
metal
– Still diffraction pattern, and not diffuse
scattering, was observed, confirming that
Thus individual electrons behave as waves
Single Electron Diffraction

27. Two-slit Interference
Thomas Young
The intensity is obtained by
squaring the wave,
I1 ~ <h1
2>, I2 ~ <h2
2>,
I1
2 = <(h1 + h2)2> = <h1
2+h2
2+ 2h1h2>,
where < > is average over time of
the oscillating wave.
h1h2 ~ cos(2p/) and reflects the
interference between waves
reaching the point from the two
slits.
When the waves arriving from
slits 1 and 2 are in phase, p = n,
and cos(2p/) = 1.
For <I1> = <I2>, I1
2 = 4I1.
When the waves from slits 1 and 2
are out of phase,  = n + /2, and
cos(2/) = -1 and I1
2 = 0.

28. Electron Diffraction, Set-Up

29. Electron Diffraction, Experiment
• Parallel beams of mono-energetic
electrons that are incident on a double slit
• The slit widths are small compared to the
electron wavelength
• An electron detector is positioned far from
the slits at a distance much greater than
the slit separation

30. Electron Diffraction, cont.
• If the detector collects
electrons for a long
enough time, a typical
wave interference
pattern is produced
• This is distinct evidence
that electrons are
interfering, a wave-like
behavior
• The interference pattern
becomes clearer as the
number of electrons
reaching the screen
increases

31. Active Figure 40.22
• Use the active figure
to observe the
development of the
interference pattern
• Observe the
destruction of the
pattern when you
keep track of which
slit an electron goes
through PLAY
ACTIVE FIGURE

32. Electron Diffraction, Equations
• A maximum occurs when
– This is the same equation that was used for
light
• This shows the dual nature of the electron
– The electrons are detected as particles at a
localized spot at some instant of time
– The probability of arrival at that spot is
determined by calculating the amplitude
squared of the sum of all waves arriving at a
point
sin
d θ mλ


33. Electron Diffraction Explained
• An electron interacts with both slits
simultaneously
• If an attempt is made to determine
experimentally through which slit the electron
goes, the act of measuring destroys the
interference pattern
– It is impossible to determine which slit the
electron goes through
• In effect, the electron goes through both slits
– The wave components of the electron are
present at both slits at the same time

34. Neutrons He atoms
C60 molecules
Other experiments showed wave nature for
neutrons, and even big molecules, which
are much heavier than electrons!!

35. Example of Electron Diffraction
• Electrons from a hot filament are incident upon a crystal at an angle φ = 30
from the normal (the line drawn perpendicular) to the crystal surface. An
electron detector is place at an angle φ = 30 from the normal. Atomic
layers parallel to the sample surface are spaced by d = 1.3 A.
• Through what voltage V must the electron be accelerated for a maximum in
the electron signal on the detector?
• Will the electrons scatter at other angle?

36. Phase Speed
• Phase velocity is the speed with which wave
crest advances:
x
t
k
k
T
v
t
kx
A phase
,
coordinate
of
t
coefficien
time,
of
t
coefficien
2
2
:
)
cos( 













37. Addition of Two Waves
)
2
sin(
)
2
cos(
2
)
sin(
)
sin(
)
,
(





 






 t
kx
A
t
kx
A
t
kx
A
t
x
y
t
kx
A
t
kx
A
t
kx
A
t
x
y 

 cos
sin
2
)
sin(
)
sin(
)
,
( 




Two sine waves traveling in the same direction:
Constructive and Destructive Interference
Two sine waves traveling in opposite directions create a standing wave
Two sine waves with different frequencies: Beats
]
2
(
2
(
sin[
]
)
2
/
(
)
2
/
cos[(
2
]
2
(
2
(
sin[
]
2
(
2
(
cos[
2
)
sin(
)
sin(
)
,
(
)
2
1
)
2
1
)
2
1
)
2
1
)
2
1
)
2
1
2
2
1
1
t
x
k
k
t
x
k
A
t
x
k
k
t
x
k
k
A
t
x
k
A
t
x
k
A
t
x
y




























38. Beat Notes and Group Velocity, vg
This represents a beat note with the amplitude of the beat moving at speed
dk
d
v
v
k
v
g
g










:
waves
of
on
distributi
continuous
of
ion
superposit
For
/
)
2
/
/(
)
2
/
(
]
2
(
2
(
sin[
]
)
2
/
(
)
2
/
cos[(
2
)
,
(
)
2
1
)
2
1
t
x
k
k
t
x
k
A
t
x
y











39. Beats and Pulses
Two tuning forks are struck simultaneously. The vibrate at 512 and 768 Hz.
(a) What is the frequency of the separation between peaks in the beat envelope?
(b) What is the velocity of the beat envelope?

40. Beats and Pulses
Two tuning forks are struck simultaneously. The vibrate at 512 and 768 Hz.
(a) What is the separation between peaks in the beat envelope?
(b) What is the velocity of the beat envelope?
(a)
The rapidly oscillating wave is multiplied by a more slowly varying envelope
with wave vector
]
2
(
2
(
sin[
]
)
2
/
(
)
2
/
cos[(
2
)
,
(
)
2
1
)
2
1
t
x
k
k
t
x
k
A
t
x
y










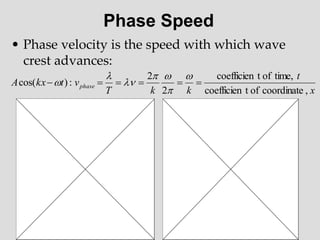
phase
beat
beat
beat
beat
beat
phase
phase
phase
phase
phase
phase
v
v
so
th
ofwaveleng
t
independen
is
sound
of
speed
ce
result
Expected
k
v
b
m
k
notes
beat
between
ce
Dis
m
k
k
k
m
v
f
v
k
m
v
f
v
k
mph
s
m
sound
of
speed
the
is
v
f
f
k
v
k
k
k

































sin
344
)
35
.
9
03
.
14
/(
)
512
768
(
2
)
2
/
/(
)
2
/
(
)
(
70
.
2
33
.
2
/
2
/
2
:
tan
33
.
2
2
/
)
35
.
9
0
.
14
(
2
/
)
(
35
.
9
344
/
512
2
/
2
/
03
.
14
344
/
768
2
/
2
/
)
770
(
/
344
,
,
)
/
2
/(
2
/
2
/
)
(
2
/
1
1
2
1
1
1
1
1
2
2
2
1
2

















41. “Construction” Particles From Waves
• Particles are localized in space
• Waves are extended in space.
• It is possible to build “localized” entities from a
superposition of number of waves with different
values of k-vector. For a continuum of waves, the
superposition is an integral over a continuum of
waves with different k-vectors.
– The wave then has a non-zero amplitude only within a
limited region of space
• Such wave is called “wave packet”

42. Wave Packet
• Mathematically a wave packet can be written as
sum (integral) of many “ideal” sinusoidal waves

43. Wave Picture of Particle
• Consider a wave packet made up of waves with a
distribution of wave vectors k, A(k), at time t. A
snapshot, of the wave in space along the x-
direction is obtained by summing over waves
with the full distribution of k-vectors. For a
continuum this is an integral.
• The spatial distribution at a time t given by:





0
)
cos(
)
(
)
,
( dk
t
kx
k
A
t
x 

44. Wave Picture of Particle
1. A(k) is spiked at a given k0, and
zero elsewhere
• only one wave with k = k0 (λ = λ0)
contributes; thus one knows
momentum exactly, and the
wavefunction is a traveling wave –
particle is delocalized
2. A(k) is the same for all k
• No distinctions for momentums, so
particle’s position is well defined -
the wavefunction is a “spike”,
representing a “very localized”
particle
3. A(k) is shaped as a bell-curve
• Gives a wave packet – “partially”
localized particle

45. Wave Picture of Particle
• The greater the range of wave numbers (and
therefore λ‘s) in the mix, the narrower the
width of the wave packet and the more
localized the particle

46. Group Velocity for Particles and Waves
• The group velocity in term of particle parameters is
• Consider a free non-relativistic particle. The total,
energy for this particle is, E = Ek = p2/2m
 
  dp
dE
p
d
E
d
dk
d
vg 





particle
particle
g
k
g
u
m
mu
m
p
v
m
p
m
p
dp
d
dp
dE
dp
dE
v















2
2

47. Group Velocity
• The group speed of wave packet is identical to the
speed of the corresponding particle,
• Is this true for photon, for which u = c?
• For photon total energy E = p·c
  c
pc
dp
d
dp
dE
vg 


dp
dE
v
u g
particle 


48. Group Velocity in Optical Fiber
A pulse of light is launched in an optical fiber. The amplitude A(k) of the pulses
is peaked in the telecommunications band at the wavelength in air,  = 1,500 nm.
The optical fiber is dispersive, with n = 1.50 + 102/, near  = 1,500 nm, where  is
expressed in nm. What is the group velocity?

49. Group Velocity in Optical Fiber
A pulse of light is launched in an optical fiber. The amplitude A(k) of the pulses
is peaked in the telecommunications band at the wavelength in air,  = 1,500 nm.
The optical fiber is dispersive, with n = 1.50 + 102/, near  = 1,500 nm, where  is
expressed in nm. What is the group velocity?
567
.
1
10
5
.
1
10
5
.
1
),
10
1
(
))
10
(
1
(
)
2
(
2
)
2
(
2
2
,
2
)
1
(
)
1
(
)
(
,
3
2
2
2
2
2
2
2
2
2
2
2
2
2


































n
n
n
c
n
n
c
dk
d
d
dn
n
c
n
c
d
dn
n
c
n
c
k
d
dn
n
c
n
c
dk
d
d
dn
n
ck
n
c
dk
d
k
dk
d
so
k
But
dk
d
d
dn
n
ck
n
c
dk
dn
n
ck
n
c
dk
n
d
ck
n
c
dk
k
n
c
d
dk
d
dk
d
v
k
n
c
n
c
k
v g
p



























