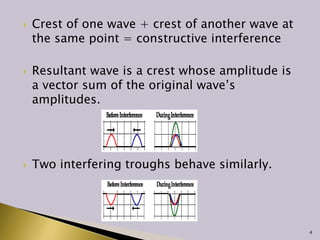
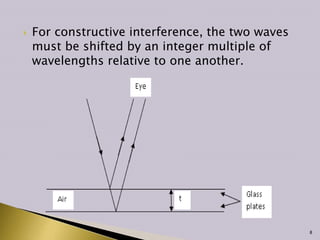
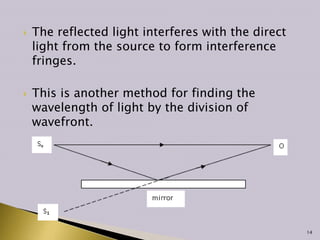
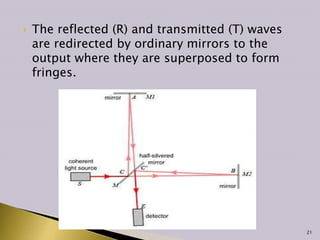
Interference occurs when two waves superimpose to form a resultant wave of greater or lower amplitude. There are two main types of interference: constructive and destructive. Constructive interference occurs when wave crests or troughs overlap, increasing amplitude, while destructive interference occurs when a crest and trough overlap, decreasing amplitude. Thin film interference is studied using thin films that reflect light, which can interfere and be analyzed to determine properties like film thickness. Interferometers exploit the interference of light to make extremely precise measurements of distance and other values.

1. INTERFERENCE
Robert Eshun
ACCRA POLYTECHNIC
1

2.  Interference
◦ interaction of two or more waves at a point in a
medium such that the disturbance in the resulting
wave is the vector sum of the disturbances in the
interfering waves.
◦ the phenomenon in which two or more waves
superpose each other to form a resultant wave of
greater or lower amplitude.
2

3.  Interference - the interaction of waves that
are coherent with each other, either because
they come from the same source or because
they have the same or nearly the same
frequency.
3

4.  Crest of one wave + crest of another wave at
the same point = constructive interference
 Resultant wave is a crest whose amplitude is
a vector sum of the original wave’s
amplitudes.
 Two interfering troughs behave similarly.
4

5.  Crest of a wave + trough of another wave =
destructive interference.
 If amplitudes of original waves are the same,
zero displacement of particles results.
5

6.  Layer of material with thickness in the sub-
nanometer to micron range.
 Light striking surface is either transmitted or
reflected at the upper surface.
 Transmitted light may also be transmitted or
reflected at bottom surface.
6

7.  Studies of these waves reveal information about
the surface including the thickness of the film or
the effective refractive index of the film medium.
 Thin film interference - the interference of waves
reflected from the top surface with those
reflected from the bottom surface.
 Thin films such as soap bubbles show colourful
patterns because of interference between light
waves.
 The thickness of the film has to be comparable to
the wavelength of light for a nice coloured
pattern to be obtained.
7

8.  For constructive interference, the two waves
must be shifted by an integer multiple of
wavelengths relative to one another.
8

9.  Thin film of air trapped between two pieces
of glass
 Monochromatic light incident almost normally
on film.
 Light is reflected from the two interfaces.
 The eye focuses these two parallel light
beams at one spot on the retina.
9

10.  Destructive interference if path difference =
odd number of ½ wavelength.
 Constructive interference if path difference =
even number of ½ wavelengths.
10

11. Additional phase difference
 A 1800 phase change on reflection from
interface between air (optically less dense)
and glass (optically dense).
 This is equivalent to an additional path
difference of 𝜆
2.
11

12. Therefore condition for
 constructive interference is
2t=(m+1⁄2)λ
 destructive interference is
2t=mλ
where m is an integer.
12

13.  Interferometer made of a metal from which
part of a beam of light is reflected. The other
part proceeds directly to the screen.
 Light from a monochromatic slit source
reflect from a glass surface at a small angle
 Appears to come from a virtual source as a
result.
13

14.  The reflected light interferes with the direct
light from the source to form interference
fringes.
 This is another method for finding the
wavelength of light by the division of
wavefront.
14

15.  Glass prism with a large angle producing two
coherent (virtual) sources for light
interference experiments.
 Wavelength λ of the incident monochromatic
radiation given by:
𝜆 =
𝑦𝑑
𝐷
15

16.  y is the fringe separation, d is the source
separation, and D is the source-screen
distance.
16

17.  Upper portion of wave refracted downward,
lower portion refracted upward.
 Refracted waves appear to come from two
different sources
 Overlap in shaded region to produce
interference fringes.
17

18.  mth bright fringe is given by
𝑦 𝑚 = 𝑚𝜆
𝐷
𝑑
y is measured from the centre of the
interference pattern.
 The wavelength of light can be determined
from measurements of fringe separation in
the interference pattern.
18

19.  Designed to split light beam into two parts
and then recombines them to form an
interference pattern.
 For obtaining accurate length measurements.
 Physical distances can be measured by
counting interference fringes that move when
one or the other of two objects are displaced.
19

20.  Beams must be mutually coherent for fringes
to be seen.
 Must have a definite phase relationship
between them.
 Mutual coherence obtained by use of a beam
splitter (partially reflecting mirror).
20

21.  The reflected (R) and transmitted (T) waves
are redirected by ordinary mirrors to the
output where they are superposed to form
fringes.
21

22.  One of the two mirrors is kept stationary
while the other is mobile.
 The path difference depends on the relative
motion of these mirrors.
 Constructive interference if the two paths
differ by a whole number of wavelengths
(including 0); strong signal at the detector.
 Destructive if they differ by a whole number
and half wavelengths (e.g., 0.5, 1.5, 2.5 ...);
weak signal.
22