Dokumen ini membahas transformasi Z dalam pengolahan sinyal digital, yang berfungsi untuk mempermudah analisis sinyal pada domain waktu dengan memetakan konvolusi ke perkalian. Terdapat definisi, sifat, dan contoh aplikasinya dalam menentukan fungsi transfer serta respons sistem pada sinyal waktu diskrit. Stabilitas sistem juga dijelaskan, termasuk pengaruh pole dan zero pada filter serta invers transformasi Z.

1. BAB III
Transformasi Z
• Transformasi Z dalam pengolahan sinyal digital mempunyai aturan yang sama dengan
Transformasi Laplace pada rangkaian dan sistem analog.
• Terdapat intuisi bahwa kadang tidak mudah menganalisis pada domain waktu.
• Mempermudah operasi pada domain waktu, konvolusi pada domain waktu dipetakan ke
perkalian pada domain Z.
• Digunakan untuk mendefinisikan fungsi transfer
• Digunakan untuk melihat respons sistem menggunakan proses table - look- up.
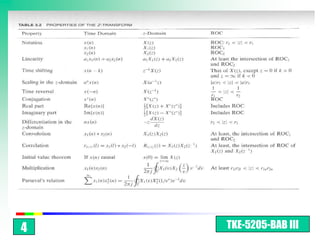
3.1.Definisi Transformasi Z
Transformasi Z sinyal waktu diskrit x(n) didefinisikan:
X ( z) x ( n) Z n (3.1.1)
z adalah variable kompleks n
Atau: X(Z) Z[x(n)] (3.1.2)
Hubungan antara x(n) dan X(z):
z
x ( n) X ( z) (3.1.3)
Untuk deret kausal:
n
X ( z) x ( n) Z (3.1.4)
n 0
1 TKE-5205-BAB III

2. Donwload slide di http://rumah-belajar.org
TKE-5205-BAB III

3. Karena transformasi Z merupakan deret yang tidak terbatas, hanya ada untuk harga z dimana
deretnya konvergen. ROC (region of Convergence) X(z) adalah himpunan seluruh harga z dimana
X(z) mempunyai harga terbatas. Oleh sebab itu pada Transformasi Z selalu juga ditentukan ROC-
nya.
Contoh:
Tentukan Transformasi Z untuk:
x(n) = 2n untuk n > 0 n
n
= 0 untuk n < 0 n n 2
X ( z) 2 Z
n 0 n 0 Z
Ini merupakan deret geometri tidak terbatas, dimana :
n
2 1 1 z
1 A A2 A3 ... untuk A < 1
n 0 Z 1 A 1 2 z 2
Z
Tugas :
1. Tentukan X(z) dan daerah konvergensinya untuk:
x(n) = (1/3)n u(n) untuk n > 0
=0 untuk n < 0
2. Tentukan transformasi Z dan daerah konvergensi dari sinyal:
x(n) =- n untuk n > 0
=0 untuk n < 0
2 TKE-5205-BAB III

4. 3.1.Sifat-sifat Transformasi Z
Linieritas
z z
Jika x ( n) X ( z) dan x ( n) X ( z) (3.2.1)
Maka berlaku:
z
.x n .y n .X z .Y z
(3.2.2)
Pergeseran deret
z
xn m z m X (z ) (3.2.3)
Konvolusi z
x n *y n X zY z
(3.2.4)
Hitung konvolusi dari :
x1(n) = {1,-2,1}
x2(n) = 1 0 < n < 5
= 0selain itu
jawaban:
X1(z) = 1-2z-1+ z-2
X2(z) = 1+ z-1+ z-2+ z-3+ z-4+ z-5
Sesuai dengan sifat konvolusi, maka: X(z) = X1(z)X2(z) = 1-z-1-z-6-z-7
Jadi: x(n) = {1,-1,0,0,0,0,-1,1}
Skala
a n x(n) z
X z / a) (3.2.5)
3 TKE-5205-BAB III

5. 4 TKE-5205-BAB III

6. 5 TKE-5205-BAB III

7. Beberapa pasangan transformasi z yang umum digunakan
6 TKE-5205-BAB III

8. L M
y(n) bi x(n i) ai x n i
i 0 i 1 (3.3.1)
Untuk mendapatkan fungsi transfer, transformasi persamaan perbedaan tersebut ke dalam
domain z:
z
X ( z ) dan y (n) Y ( z)
z
x ( n)
sehingga diperoleh: Y ( z ) L b X ( z ) z 1 M a Y z z 1
i i
i 0 i 1
L M
bi X ( z ) z 1
Y ( z) 1 aiY z z 1 (3.3.2)
i 0 i 1
Fungsi transfer, H(z) didefinisikan sebagai:
1 2 L
Y ( z) b0 b1 z b2 z ... bL z
H ( z) 1 2 M
(3.3.3)
X ( z) a0 a1 z a2 z ... aM z
L
i
bi z
i 0
H ( z) M
i
ai z
i 1
7 TKE-5205-BAB III

9. 3.1.1. Fungsi Transfer dan Respons Impulse
Konvolusi dipetakan ke perkalian dalam domain z. x n * y n z X z Y z
Dapat dilihat bahwa fungsi transfer H(z) ada hubungannya dengan deret respons impulse h(n),
yaitu:
H ( z) h( n) z n
atau n 0
z
h( n ) H ( z)
Contoh:
Tentukan fungsi transfer dari filter IIR orde satu di bawah ini:
Langkah 1: tulis persamaan perbedaannya:
y(n) = 0.2 x(n) + 0.8 y(n-1)
Langkah 2: transfromasikan seluruh sinyal ke transformasi z,
z z
y(n) Y ( z) x ( n) z
X ( z) y(n 1) z 1Y ( z)
Langkah ketiga: karena transformasi z adalah operasi linier maka dapat
ditulis:
Y(z) = 0.2 X(z) + 0.8 z-1 Y(z)
Langkah keempat: bentuk rasio Y(z)/Z(z) sehingga diperoleh fungsi transfer.
8 TKE-5205-BAB III

10. Y ( z) 0.2 0.2 z
H ( z) 1
X ( z) 1 0.8 z z 0.8
z 0.2 z
h(n) 0,2.0,8n u(n) H ( z) z 0.8
z 0,8
Fungsi Transfer Sistem FIR
L
1 L k
H ( z ) b0 b1 z ... bL z bk z
k 0
atau:
L
n
H ( z) bn z (3.3.4)
n 0
sehingga untuk Filter FIR:
{h(0), h(1),… h(L)}={b0, b1,…, bL}
Realisasi Filter Ekivalen
9 TKE-5205-BAB III

11. 3.3.2 Pole dan Zero fungsi transfer H(z)
Secara umum fungsi transfer adalah rasional, dan mempunyai polynomial yang dibagi
(numerator) dan pembagi (denumerator).
Akar-akar dari polynomial numerator dan denumerator disebut dengan zero dan pole.
Pole-zero pembentuk H(z) sangat diperlukan dalam analisis sinyal dan desain filter.
L
( z zk )
N ( z) k 0
H ( z) G
D( z ) M
(z pk )
k 0
dimana G adalah faktor Gain
Contoh:
0.2 z
H ( z)
z 0.8
Bagian imajiner
X
Bagian real
10 TKE-5205-BAB III

12. • Zero (O) dari fungsi transfer di atas adalah 0
• Sedangkan pole (X) dari fungsi tranfsfer di atas adalah 0.8
Pole Zero pada Sistem Orde 2
1 1.3435z 1 0.9025z 2
H ( z)
1 0.45z 1 0.55z 2 Im
X
0 0
( z .95e j 45 )(z .95e j 45 )
Re
H ( z) 0 0
( z .7416e j 72.34 )(z .95e j 72.34 ) X
X  Pole
Z  Zero
Catatan: Koefisien filter berharga real, dan oleh sebab itu pole dan zero berasal dari
pasangan konjugate kompleks.
11 TKE-5205-BAB III

13. 3.3.3 Stabilitas Pole dan Zero
Pole erat hubungannya dengan stabilitas filter karena berhubungan dengan
impulse respons sistem. Secara grafis, untuk mencapai kestabilannya maka pole
harus terletak di dalam lingkaran dengan jari-jari 1, yaitu:
|Pi| < 1 untuk seluruh i = 1, 2, …, M
Filter IIR dapat terbentuk oleh seluruh pole atau oleh pole dan zero dan hal yang
terpenting adalah stabilitas. FIR atau disebut dengan filter yang terbentuk dari zero
seluruhnya selalu stabil.
12 TKE-5205-BAB III

14. 3.3.4 Fungsi Frekuensi Respons
1 L
b0 b1 z ... bL z
H ( z) 1 M
a0 a1 z ... a M z
dengan mengganti z = ej
j j L
jw b0 b1e ... bL z
H (e ) j j M
a0 a1 z ... a M z
Fungsi respons frekuensi magnitude
L
(e j zk )
jw k 0
H (e ) G
M
(e j pk )
k 0
Fungsi respons frekuensi fasa
L M
arg(H (e j )) arg e j zk arg e j zz
k 0 k 0
13 TKE-5205-BAB III

15. Pengaruh pole dan zero pada H(ej )
•- Pole menyebabkan terbentuk puncak pada magnitude respons frekuensi
•- Zero menyebabkan terbentuknya lembah pada magnitude respons frekuensi
•- Filter yang sangat selektif didesain secara efisien dengan cara menempatkan pole
sedekat mungkin dengan lingkaran z=1.
•- Derajat turunan yang tajam diperoleh dengan cara menempatkan zero dekat
dengan lingkaran z=1.
•- Jika filter yang dibuat hanya menggunakan pole, derajat turunan yang tajam
memerlukan pole yang banyak (derajat tinggi)  tidak efisien.
•- Jika filter yang dibuat hanya menggunakan zero maka pada respons frekuensi
untuk mendapatkan puncak yang tajam memerlukan zero yang banyak  tidak
efisien
14 TKE-5205-BAB III

16. Respons Fasa dan Magnitude
Hubungan Lokasi zero dan respons frekuensi
15 TKE-5205-BAB III

17. Pengaruh lokasi Pole terhadap respons frekuensi
3.4 Transformasi Z Inverse
n z z
pk , n 0 , z pk
z pk
n z z
pk , n 0 , z pk
z pk
jw b0 z L b1 z L 1
... bL
H (e ) L L 1
a0 z a1 z ... a M
z z
H ( z ) c0 c1 ... cM
z p1 z pM
16 TKE-5205-BAB III

18. Gunakan partial Fraction
z2 z
H ( z)
5 1
Z2 z
6 6
Dengan ROC |z| > ½ Dan 1
n
1
n
h( n) 9 8 n 0
2 3
z z
H ( z) 9 8
1 1
z z
2 3
Contoh:
ROC 1/3 < |z| < ½
h(n) = -8(1/3)n n>0
h(n) = -9(1/2)n n<0
Untuk ROC |z| < 1/3
h(n) = 8(1/3)n –9(1/2)2 , n<0
17 TKE-5205-BAB III

19. 3.4.1 Invers Transformasi Z menggunakan teori Residu
Kita batasi pada deret kausal, transformasi Z:
n
X ( z) x ( n) z
n 0
Jika integrasi berlawanan arah dengan jarum jam yang berada dalam ROC dan
termasuk di dalam lingkaran satuan, maka.
X ( z ) z k 1dz x ( n) z k n 1
dz
c Cn 0
Jika dekat dengan origin:
X ( z ) z k 1dz x ( n) z k n 1
dz
c n 0 C
sehingga:
zk n 1
dz 2 . j. .(k n)
C
Teori keadaan Residu Cauchy untuk polynomial rasional X(z)
1
x ( n) X ( z ).z n 1dz
2 .j C
18 TKE-5205-BAB III

20. A( z )
X ( z)
z p1 z p 2 ... z pN
N
x ( n) Re s z n 1 X ( z ) z p1
i 1
1 dm 1
Re s z n 1 X ( z ) z p z pi m z n 1 X ( z )
1 (m 1)! dz m 1
z pi
Re s z n 1 X ( z ) z p z pi z n 1 X ( z ) z p
1 i
Contoh:
z
X ( z)
z a
z
Re s z n 1 X ( z ) z p1 z a zn 1
an
z a z a
z2
X ( z) 2
z a
19 TKE-5205-BAB III

21. n 1 d 2 n 1 z2
Re s z X ( z) z a z a z 2
n 1 an
dz z a z a
z2
H ( z) 2
1
z
6
|z| > 1/6 h(n) = ( n+ 1 )(1/6)n, n>0
|z| < 1/6 h(n) = -( n+ 1 )(1/6)n, n<0
20 TKE-5205-BAB III

22. 3.4 Inverse Z Transform
n z z
pk , n 0 , z pk
z pk
n z z
pk , n 0 , z pk
z pk
3.4.1 Mencari Respons Impulse menggunakan Invers Transformasi Z
Akar persamaan
b0 z L b1 z L 1 ... bL
H ( z)
a0 z L a1 z L 1 ... a M
z z
H ( z) c0 c1 ... c M
z p1 z pM
Contoh:
z2 z
H ( z)
5 1
Z2 z
6 6
21 TKE-5205-BAB III

23. Cari akar persamaannya, diperoleh:
z z
H ( z) 9 8
1 1
z z
2 3
Dengan ROC |z| > ½
Respons Impulsenya adalah:
n n
1 1
h ( n) 9 8 n 0
2 3
Contoh:
ROC 1/3 < |z| < ½
h(n) = -8(1/3)n n>0
h(n) = -9(1/2)n n<0
Untuk ROC |z| < 1/3
h(n) = 8(1/3)n –9(1/2)2 , n<0
Invers Transformasi Z menggunakan Teori Residu
Dibatasi pada deret kausal, transformasi Z:
X ( z ) z k 1dz x(n) z k n 1dz
X ( z) x(n) z n
c Cn 0
n 0
22 TKE-5205-BAB III

24. Jika integrasi berlawanan arah dengan jarum jam yang berada dalam ROC dan
termasuk di dalam lingkaran satuan, maka.
X ( z ) z k 1dz x(n) z k n 1dz
c n 0 C
Jika dekat dengan origin:
z k n 1dz 2 . j. .(k n)
C
sehingga:
1
x ( n) X ( z ).z n 1dz
2 .j C
Teori keadaan Residu Cauchy untuk polynomial rasional X(z)
A( z )
X ( z)
z p1 z p2 ... z pN
N
x(n) Re s z n 1 X ( z ) z pi
i 1
1 dm 1
Re s z n 1 X ( z ) z p z pi m z n 1 X ( z )
1 (m 1)! dz m 1
z pi
Re s z n 1 X ( z ) z p z pi z n 1 X ( z ) z p
1 i
23 TKE-5205-BAB III

25. Contoh:
z
X ( z)
z a
z
Re s z n 1 X ( z ) z p z a zn 1 an
1 z a z a
z2
X ( z)
z a2
d z2
Re s z n 1 X ( z ) z a z a 2 zn 1 n 1 an
dz 2
z a
z a
z2
H ( z)
2
1
z
6
24 TKE-5205-BAB III

26. |z| > 1/6 h(n) = ( n+ 1 )(1/6)n, n>0
|z| < 1/6 h(n) = -( n+ 1 )(1/6)n, n<0
3z
H ( z) z
z 0.7 X ( z)
( z 1)
3z 2
Y ( z) H z X z
z 1 z 0.7
y(n) Re s z n 1Y ( z ) z 1 Re s z n 1Y ( z ) z 0.7
( z 1) z n 1z 2 ( z 0.7) z n 1z 2
y(n) 3 3
z 0.7 z 1 z 1 z 0.7
z 1 z 0.7
y(n) 10 7(0.7) n n 0
25 TKE-5205-BAB III

27. Donwload slide di http://rumah-belajar.org
TKE-5205-BAB III