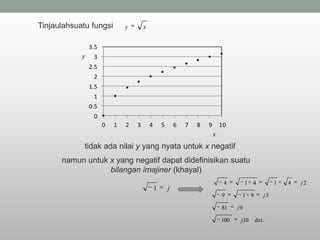
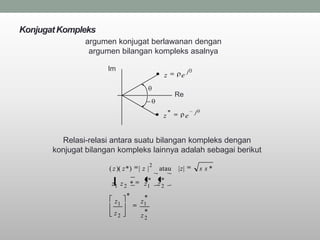
Bilangan kompleks dapat didefinisikan sebagai pasangan bilangan nyata (x,y) dimana x adalah bagian nyata dan y adalah bagian khayal. Bilangan kompleks dapat digambarkan pada bidang kompleks dengan sumbu x sebagai sumbu nyata dan sumbu y sebagai sumbu khayal. Bilangan kompleks dapat dilakukan operasi aljabar seperti penjumlahan, pengurangan, perkalian, dan pembagian dengan mengoperasikan masing-masing

1. BILANGAN KOMPLEKS

2. Definisi
Dalam buku Erwin Kreyszig kita baca definisi bilangan bilangan kompleks
sebagai berikut
Bilangan kompleks z ialah suatu pasangan terurut (x,y)
dari bilangan nyata x, y, yang kita tuliskan
z ( x, y )
bagian nyata (real part) bagian khayal (imaginary part)
dari z dari z
kita tuliskan Re z x Im z y
Kita akan mencoba memahami definisi ini secara grafis,
mulai dari pengertian tentang bilangan nyata.

3. Bilangan Nyata
Kita mengenal bilangan nyata bulat seperti 1, 2, 3 dan seterusnya;
bilangan nyata pecahan ¼, ½, ¾ dan seterusnya, serta bilangan nyata
yang hanya dapat di angankan seperti . Walaupun hanya dapat
diangankan, bilangan ini tetap nyata, nilainya adalah 3,14……., dengan
angka desimal yang tak diketahui ujungnya.
Secara grafis, bilangan nyata dapat digambarkan posisinya di suatu
sumbu yang disebut sumbu nyata,
| | | | | | | | m
-2 -1 0 1 2 3 4 5

4. Tinjaulahsuatu fungsi y x
3.5
y 3
2.5
2
1.5
1
0.5
0
0 1 2 3 4 5 6 7 8 9 10
x
tidak ada nilai y yang nyata untuk x negatif
namun untuk x yang negatif dapat didefinisikan suatu
bilangan imajiner (khayal)
4 1 4 1 4 j2
1 j
9 1 9 j3
81 j9
100 j10 dst.

5. Kita dapat memandang j sebagai sebuah operator; artinya jika j
beroperasi pada bilangan nyata 5 misalnya, kita mendapatkan bilangan
imajiner j5 dan jika beroperasi pada bilangan nyata b kita mendapatkan
bilangan imajiner jb
Sumbu tegak tegak lurus pada sumbu-nyata untuk memosisikan
bilangan imajiner; sumbu ini disebut sumbu imajiner
bidang sekarang dibatasi oleh sumbu nyata (diberi tanda Re) dan
sumbu imajiner (diberi tanda Im); dan disebut bidang kompleks
setiap titik di bidang kompleks menunjukkan posisi bilangan-kompleks
(x,,y)
dengan x adalah komponen nyata dan y adalah komponen imajiner-nya

6. Pernyataan Bilangan Kompleks
satu bilangan kompleks z merupakan jumlah dari komponen nyata
dan komponen imajiner dan dituliskan
z a jb
bilangan kompleks bagian imajiner
bagian nyata
Im
z a jb z (cos j sin )
disebut modulus jb
2 2
modulus z a b
b sin
2 2
z a b (cos j sin )
a Re
disebut argumen
1 b a cos
arg z tan
a

7. CONTOH
Suatu bilangan kompleks dinyatakan sebagai
z1 3 j4
Sudut dengan sumbu nyata adalah
1 o
1 tan ( 4 / 3) 53 ,1
Pernyataan z1 dapat kita tuliskan
2 2 o o
z1 3 4 cos 53 ,1 j sin 53 ,1
o o
5 cos 53 ,1 j sin 53 ,1

8. CONTOH
Suatu bilangan kompleks dinyatakan sebagai
o o
z2 10 cos 20 j sin 20
Pernyataan ini dapat kita tuliskan
o o
z2 10 cos 20 j sin 20
10 ( 0 , 94 j 0 , 34 ) 9,4 j 3, 4 )

9. Kesamaan Bilangan Kompleks
2 2
Modulus a b merupakan nilai mutlak
Dua atau lebih bilangan kompleks bisa saja memiliki nilai yang
sama akan tetapi dengan sudut yang berbeda; atau sebaliknya
mempunyai nilai sama akan tetapi memiliki yang berbeda.
Dua bilangan kompleks dikatakan sama besar jika mereka
mempunyai baik maupun yang sama besar.
Dengan kata lain, mereka memiliki bagian nyata dan bagian
imajiner yang sama besar..

10. Negatif dari Bilangan Kompleks
Nilai negatif dari suatu bilangan kompleks adalah
nilai negative dari kedua komponennya
Jika z a jb maka z a jb
Im
jb z a jb
o
180
a Re
z a jb

11. CONTOH
Jika z1 4 j6 maka z2 z1 4 j6
Sudut dengan sumbu nyata
1 o
1 tan (6 / 4) 56 ,3
o o o
2 56 ,3 180 236 ,3
z1 dapat dinyatakan sebagai
2 2 o o
z1 4 6 cos 56 , 3 j sin 56 ,3
o o
7 , 2 cos 56 , 3 j sin 56 ,3
o o o o
z1 7 , 2 cos( 56 , 3 180 ) j sin( 56 , 3 180 )
7 ,2 0 , 55 j 0 ,83 3 , 96 j6

12. Konjugat Bilangan Kompleks
Konjugat dari suatu bilangan kompleks z adalah bilangan kompleks z*
yang memiliki komponen nyata sama dengan z tetapi komponen
imajinernya adalah negatif dari komponen imajiner z.
Jika z a jb maka z a jb
Im
jb z a jb
Re
a
jb z a jb

13. CONTOH:
Jika z 5 j6 maka z 5 j6
Im
Sudut dengan sumbu nyata z 5 j6
1 o
tan (6 / 5) 50 , 2
o Re
50 , 2
z dapat dinyatakan sebagai z* 5 j6
2 2 o o
z 5 6 cos 50 , 2 j sin 50 , 2
o o
7 ,8 cos 50 , 2 j sin 50 , 2
o o
z 7 ,8 cos 50 , 2 j sin 50 , 2

14. CONTOH:
Im
z 5 j6
Jika z 5 j6 maka z 5 j6 Re
z 5 j6
Im
z 5 j6
Jika z 5 j6 maka z 5 j6
Re
z 5 j6

15. Operasi-Operasi Aljabar

16. Penjumlahan dan Pengurangan Bilangan Kompleks
Hasil penjumlahan dua bilangan kompleks merupakan bilangan
kompleks yang komponen nyatanya merupakan jumlah komponen nyata
dan komponen imajinernya juga merupakan jumlah komponen imajiner.
z1 z2 ( a1 jb1 ) (a2 jb 2 )
( a1 a2 ) j ( b1 b2 )
Hasil selisih dua bilangan kompleks adalah bilangan kompleks yang
komponen nyatanya merupakan selisih komponen nyata dan
komponen imajinernya juga merupakan selisih komponen imajiner.
z1 z2 ( a1 jb1 ) (a2 jb 2 )
( a1 a2 ) j ( b1 b2 )

17. CONTOH:
Diketahui s1 2 j3 dan s2 3 j4
s1 s2 (2 j 3) (3 j 4)
5 j7
s1 s2 (2 j 3) (3 j 4)
1 j1

18. Perkalian Bilangan Kompleks
Perkalian dua bilangan kompleks dilaksanakan seperti halnya kita
melakukan perkalian jumlah dua bilangan, yaitu dengan malakukan
perkalian komponen per komponen
( z 1 )( z 2 ) ( a1 jb 1 )( a 2 jb 2 )
a1 a 2 jb 1 a 2 jb 1 a 2 b1 b 2
a1 a 2 2 jb 1 a 2 b1 b 2
Jika z 2 z1
z1 z1 (a jb )( a jb )
2 2
a jba jba b
2 2
a b
2 2
Perhatikan: z1 z1 z1 a jb
2
2 2 2 2
a b a b

19. CONTOH: z1 2 j3 dan z2 3 j4
( z1 )( z 2 ) (2 j 3 )( 3 j 4)
6 j8 j9 12
6 j17
CONTOH: z1 2 j3 dan z2 z1 2 j3
( z1 )( z1 ) (2 j 3 )( 2 j 3)
4 j6 j6 9
4 9 13
2
2 2 2
z1 z1 z1 2 3 4 9 13

20. Pembagian Bilangan Kompleks
Hasil bagi suatu pembagian tidak akan berubah jika
pembagian itu dikalikan dengan 1
z1 a1 jb 1 a2 jb 2
z2 a2 jb 2 a2 jb 2 a2 jb 2
1
( a1 a 2 b1b 2 ) j ( b1 a 2 b 2 a1 ) a2 jb 2
2 2
a2 b2
CONTOH: z1 2 j3 dan z2 3 j4
z1 2 j3 3 j4 (6 12 ) j( 8 9) 18 1
j
z2 3 j4 3 j4 2 2 25 25
3 4

21. Pernyataan Bilangan Kompleks Bentuk Polar

22. Fungsi Eksponensial Kompleks
Jika x adalah bilangan nyata maka fungsi ekponensial
x
y e
merupakan fungsi ekponensial nyata;
y memiliki nilai nyata
Jika z adalah bilangan kompleks z j
fungsi eksponensial kompleks didefinisikan
z ( j )
e e e (cos j sin ) ;
dengan e adalah fungsi eksponensi al riil`
j
Melalui identitas Euler e cos j sin
fungsi exponensial kompleks dapat kita tuliskan
z j
e e e

23. Bentuk Polar
Representasi bilangan kompleks dalam bentuk polar adalah
j
z e
Im
j
z e
arg z z
Re
CONTOH: Misalkan suatu bilangan kompleks z = 10 e j0,5
Modulus bilangan kompleks ini adalah |z| = 10 dan
argumennya z = 0,5 rad
Im
Bentuk sudut sikunya adalah:
j 0 ,5
z 10 (cos 0 , 5 j sin 0 , 5 ) z 5e
10
10 ( 0 ,88 j 0 , 48 ) 8 ,8 j 4 ,8 0 ,5 rad
Re

24. CONTOH:
Misalkan suatu bilangan kompleks z = 3+ j4
2 2
Modulus |z| 3 4 5
1 4
Argumen z tan 0 ,93 rad
3
Representasi polar z = 5e j0,93
Im
j 0 , 93
z 5e
5
0 ,93 rad
Re

25. CONTOH:
Misalkan z 2 j0
Modulus |z| 4 0 2
1
Argumen tan 0/ 2 tidak bernilai tunggal
Di sini kita harus memilih = rad
karena komponen imajiner 0
sedangkan komponen nyata 2
Im
j
z 2e
Re
2

26. .
CONTOH:
Misalkan z 0 j2
Modulus | z | 0 4 2
1
Argumen tan 2/0 /2
komponen imajiner 0
komponen nyata 2
Representasi polar adalah Im
j /2
z 2e
Re
j /2
j2 z 2e

27. Manfaat Bentuk Polar

28. Perkalian dan Pembagian Bilangan Kompleks
Representasi polar dari bilangan kompleks mempermudah
operasi perkalian dan pembagian.
j j j
( z1 )( z 2 ) z1 1e
1
1e 2e
1 2
1 j( )
j
e 1 2
j( ) z2 2e
2
2
2e
1 2
1
CONTOH:
Misalkan z1 = 10 e j0,5 dan z2 = 5 e j0,4
j 0 ,5 j 0,4 j 0 ,9
z1 z 2 10 e 5e 50 e
j 0 ,5
z1 10 e j 0 ,1
2e
z2 j 0,4
5e

29. Konjugat Kompleks
argumen konjugat berlawanan dengan
argumen bilangan kompleks asalnya
Im j
z e
Re
j
z e
Relasi-relasi antara suatu bilangan kompleks dengan
konjugat bilangan kompleks lainnya adalah sebagai berikut
2
( z )( z *) |z| atau |z| s s*
* *
z1 z 2 * z1 z2
* *
z1 z1
z2 *
z2

30. CONTOH:
j 0 ,5 j 0,4
Misalkan z1 10 e dan z2 5e
j 0 ,5 j 0 ,5
z1 z1 10 e 10 e 100
z2 z2 25
j 0 ,5 j 0,4 j 0 ,9 j 0 ,9
z1 z 2 10 e 5e 50e 50e
j 0 ,5 j 0,4 j 0 ,9
10 e 5e 50 e
j 0 ,5
z1 10 e j 0 ,1 j 0 ,1
2e 50e
z2 j 0,4
5e
j 0 ,5
10 e j 0 ,1
2e
j 0,4
5e

31. Course Ware
Bilangan Kompleks
Sudaryatno Sudirham