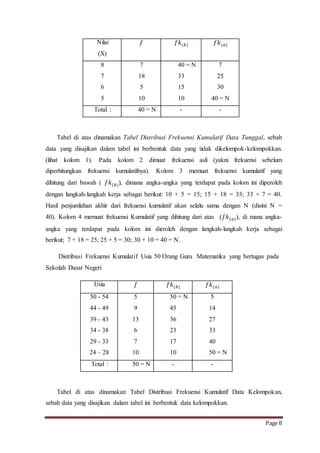
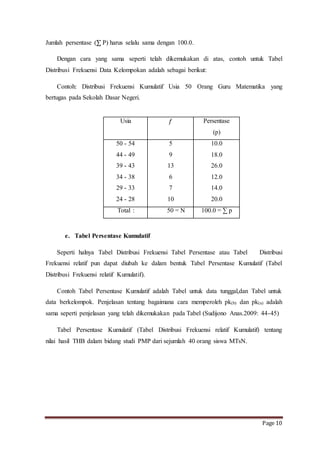
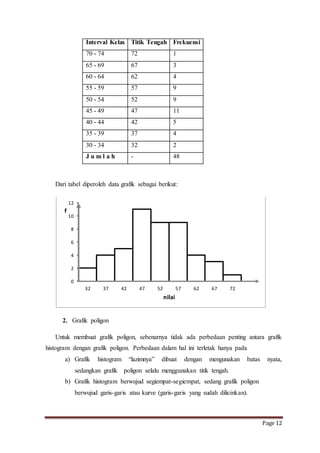
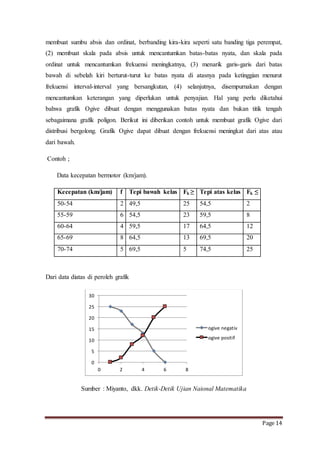
Dokumen ini membahas pengertian data, frekuensi, dan distribusi frekuensi, serta pentingnya penyajian data statistik untuk memberikan informasi yang jelas. Tabel distribusi frekuensi, baik tunggal maupun berkelompok, dijelaskan sebagai alat untuk menyajikan data dan memudahkan analisis. Selain itu, grafik distribusi frekuensi seperti histogram juga disebutkan sebagai metode visualisasi data.