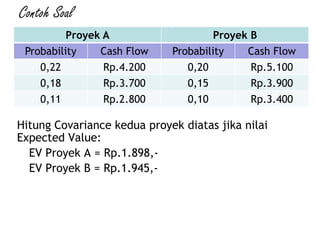
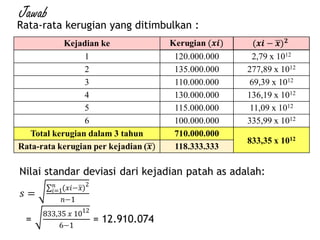
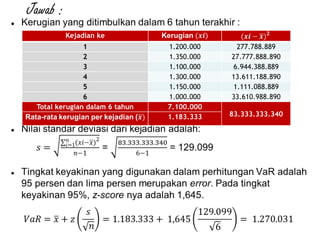
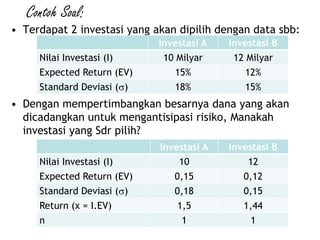
Dokumen ini membahas analisis risiko menggunakan pendekatan kualitatif dan kuantitatif dalam manajemen risiko, termasuk identifikasi risiko, penilaian risiko, dan perbaikan risiko. Berbagai alat analisis, seperti Model Capital Asset Pricing dan Value at Risk, digunakan untuk menghitung return yang diharapkan, varians, dan deviasi standar untuk mengevaluasi pilihan investasi. Contoh soal dan perhitungan disediakan untuk menunjukkan penerapan teori analisis risiko dalam keputusan investasi.

1. ANALISIS RISIKO
Y. Rahmat Akbar, SE, M.Si
http://yrasemsi.blogspot.co.id/
DENGAN PENDEKATAN KUALITATIF DAN KUANTITATIF

2. TAHAP-TAHAP MANAJEMEN RISIKO
Risk
Identification
Risk
Assessment
Risk
Insight
Risk
Improvement

3. ALAT ANALISIS MANAJEMEN RISIKO
1938
1952
1963
1966
1973
1979
MARKOWITZ MEAN-
VARIANCE FRAMEWORK
MULTIPLE FACTOR MODEL
BINOMIAL OPTION MODEL
BOND DURATION
SHARPE CAPITAL ASSET
PRICING MODEL (CAPM)
BLACK-SCHOLES OPTION
PRICING MODEL
1983
1986
1988
1992
1993
1994
LIMITS ON EXPOSURES BY
DURATION BUCKET
STRESS TESTING
RISK METRICS
RISK ADJUSTED RETURN
ON CAPITAL(RAROC)
RISK WEIGHTED ASSETS
FOR BANKS
VALUE AT RISK (VAR)
1997
1998
2000
INTEGRATION OF CREDIT AND
MARKET RISK
CREDIT METRICS/RISK
ENTERPRISEWIDE RISK
MANAGEMENT

4. 1
PENDEKATAN KUANTITATIF
DALAM ANALISIS RISIKO

5. EXPECTED VALUE /
EXPECTED RETURN

6. RETURN
MERUPAKAN HASIL YANG DIPEROLEH
DARI INVESTASI ATAU DISEBUT JUGA
TINGKAT PENGEMBALIAN/KEUNTUNGAN

7. RETURN DAPAT BERUPA :
• Realized return (return realisasi), merupakan
return yang telah terjadi. Return ini dihitung
berdasarkan data historis.
• Expected return (return ekspektasi),
merupakan return yang diharapkan akan
diperoleh oleh investor dimasa mendatang.

8. RETURN YANG DIHARAPKAN (EXPECTED RETURN)
• Merupakan rata2 tertimbang dari distribusi
probabilitas.
• EV yang lebih besar menunjukkan keuntungan yang
akan diperoleh lebih tinggi. Begitu juga sebaliknya.
n
EV = ∑ Ri . Pri
i=1
EV = tingkat keuntungan yang diharapkan
(expected value atau expected return)
Ri = tingkat keuntungan atau cash flow pada kondisi i
Pri = probabilitas kondisi i terjadi

9. Contoh
Pengukuran Risiko Tunggal Dgn Return Yg Diharapkan
Return yg diharapkan:
Wings: EV = (30%x0.3) + (15%x0.4) + (5%x0.3)
= 0,165 atau 16,5%
Indofood: EV = (20%x0.3) + (15%x0.4) + (10%x0.3)
= 0,15 atau 15%
Maka yang dipilih adalah investasi yang memiliki return/keuntungan
yang lebih tinggi yaitu PT. Wings dengan return 16,5%
Keadaan
Ekonomi
Probabilitas
Kejadian
Rate of Return on Stock
PT Wings PT Indofood
Booming 0.3 30% 20%
Normal 0.4 15% 15%
Resesi 0.3 5% 10%

10. Contoh Soal
Jawab :
EVA = 0,22(4.200) + 0,18(3.700) + 0,11(2.800)
= 1.898
EVB = 0,20(5.100) + 0,15(3.900) + 0,10(3.400)
= 1.945
Maka proyek yang dipilih adalah yang menghasilkan keuntungan
yang lebih besar yaitu proyek B dengan keuntungan Rp.1.945
Proyek A Proyek B
Probability Cash Flow Probability Cash Flow
0,22 Rp.4.200 0,20 Rp.5.100
0,18 Rp.3.700 0,15 Rp.3.900
0,11 Rp.2.800 0,10 Rp.3.400

11. Dengan hanya
berdasarkan kalkulasi
expected return,
investasi mana yang
anda pilih?

12. Sudahkah anda
mempertimbangkan
RISIKO?

13. VARIANS

14. VARIANS RETURN
MERUPAKAN PENYERAPAN DARI PENYEBARAN
PROBABILITAS

15. • Merupakan selisih pendapatan, biaya dan
keuntungan terhadap jumlah yang direncanakan.
• Varians yang lebih tinggi menunjukkan sebaran
risiko yang akan diterima lebih tinggi. Begitu juga
sebaliknya.
Varians Return (2) = (Ri – EV)2 x Pri
Dimana :
Ri = tingkat keuntungan/return ke i yang
mungkin terjadi
EV = keuntungan yang diharapkan
(expected return)
Pri = Probabilitas kejadian return ke-i
VARIANS

16. Contoh Soal
Jawab :
EVA = 0,11 x 2.800 = 308
EVB = 0,10 x 3.400 = 340
2
A = (2.800-308)2 x 0,11
= (2.492)2 x 0,11 = Rp. 683.107,-
2
B = (3.400-340)2 x 0,10
= (3.060)2 x 0,10 = Rp. 936.360,-
Maka proyek yang dipilih adalah yang memiliki nilai varians
yang lebih kecil yaitu proyek A dengan risiko kerugian
Rp.683.107
Proyek A Proyek B
Probability Cash Flow Probability Cash Flow
0,11 Rp.2.800 0,10 Rp.3.400

17. Contoh Soal :
Hitung varians return masing-masing investasi pada PT. Wings
dan PT. Indofood dengan nilai Expected Value:
Wings: EV = 0,165 atau 16,5%
Indofood: EV = 0,15 atau 15%
Keadaan
Ekonomi
Probabilitas
Kejadian
Rate of Return on Stock
PT Wings PT Indofood
Booming 0.3 30% 20%
Normal 0.4 15% 15%
Resesi 0.3 5% 10%

18. Jawab : 1. Perhitungan Varians Return PT. Wings
Probabilitas
Kejadian (Pri)
Rate of Return PT
Wings (Ri) (Ri - EV)2 (Ri - EV)2 x Pri
0,3 30%
0,4 15%
0,3 5%
Expected Return
( EV ) 16,5% Varians
Probabilitas
Kejadian (Pri)
Rate of Return PT
Indofood (Ri) (Ri - EV)2 (Ri - EV)2 x Pri
0,3 20%
0,4 15%
0,3 10%
Expected Return
( EV ) 15% Varians
2. Perhitungan Varians Return PT. Indofood

19. Jawab : 1. Perhitungan Varians Return PT. Wings
Probabilitas
Kejadian (Pri)
Rate of Return
PT Wings (Ri) (Ri - EV)2 Varians
0,3 30% 0,018225 0,0054675
0,4 15% 0,000225 0,00009
0,3 5% 0,013225 0,0039675
Expected
Return ( EV ) 16,5% Total Varians 0,009525
Probabilitas
Kejadian (Pri)
Rate of Return PT
Indofood (Ri) (Ri - EV)2 Varians
0,3 20% 0,0025 0,00075
0,4 15% 0 0
0,3 10% 0,0025 0,00075
Expected
Return ( EV ) 15% Total Varians 0,0015
2. Perhitungan Varians Return PT. Indofood

20. Varians Return pada Investasi PT Wings = 0,009
Varians Return pada Investasi PT Indofood = 0,001
2 PT Wings > 2 PT Indofood
maka investasi yang dipilih adalah investasi pada PT.
Indofood karena memiliki sebaran risiko yang lebih
kecil daripada investasi pada PT.Wings
Rekomendasi :

21. STANDARD DEVIASI

22. STANDARD DEVIASI
ADALAH SUATU ESTIMASI PROBABILITAS PERBEDAAN
RETURN NYATA (REALIZED RETURN) DARI RETURN
YANG DIHARAPKAN (EXPECTED RETURN)

23. DEVIASI STANDAR (SIMPANGAN BAKU)
Standar deviasi yang lebih tinggi menunjukkan
rentang risiko yang akan diterima lebih tinggi.
Begitu juga sebaliknya.

24. Contoh Soal :
Hitung standard deviasi masing-masing investasi pada PT.
Wings dan PT. Indofood dengan nilai Expected Value:
Wings: EV = 0,165 atau 16,5%
Indofood: EV = 0,15 atau 15%
Keadaan
Ekonomi
Probabilitas
Kejadian
Rate of Return on Stock
PT Wings PT Indofood
Booming 0.3 30% 20%
Normal 0.4 15% 15%
Resesi 0.3 5% 10%

25. Jawab : Perhitungan Deviasi Standard PT. Wings
Probabilitas
Kejadian (Pri)
Rate of Return
PT Wings (Ri) (Ri - EV)2 (Ri - EV)2 x Pri
0,3 30% 0,018225 0,0054675
0,4 15% 0,000225 0,00009
0,3 5% 0,013225 0,0039675
Varians 0,009525
Standar Deviasi 0,098 atau 9,8%
Expected
Return ( EV ) 16,5%

26. Maka investasi yang dipilih adalah yang memiliki
standard deviasi yang lebih kecil yaitu investasi pada
PT.Indofood
Probabilitas
Kejadian (Pri)
Rate of Return PT
Indofood (Ri) (Ri - EV)2 (Ri - EV)2 x Pri
0,3 20% 0,0025 0,00075
0,4 15% 0 0
0,3 10% 0,0025 0,00075
Varians 0,0015
Standar Deviasi 0,039atau 3,9%
Expected
Return ( EV ) 15%
Jawab : Perhitungan Deviasi Standard PT. Indofood

27. Contoh Soal
Hitung standard deviasi masing-masing Proyek A dan B
jika nilai Expected Value:
EV Proyek A = Rp.1.898,-
EV Proyek B = Rp.1.945,-
Proyek A Proyek B
Probability Cash Flow Probability Cash Flow
0,22 Rp.4.200 0,20 Rp.5.100
0,18 Rp.3.700 0,15 Rp.3.900
0,11 Rp.2.800 0,10 Rp.3.400

28. COEFFICIENT OF VARIATION

29. COEFFICIENT OF VARIATION
MENUNJUKKAN RISIKO PER UNIT OF RETURN
DAN MENUNJUKKAN PERBANDINGAN YANG
BERARTI KETIKA RETURN YG DIHARAPKAN UNTUK
DUA PILIHAN INVESTASI TIDAK SAMA

30. KOEFISIEN VARIASI
• Merupakan ukuran penyebaran relatif atau
risiko relatif yang terdapat pada dua pilihan
investasi.
CV = σ/ EV
CV yang lebih tinggi menunjukkan tingkat
risiko yang akan diterima lebih tinggi.
Begitu juga sebaliknya.

31. KOEFISIEN VARIASI
Cnth: Apabila terdapat 2 proyek, A&B.
A B
Return yg diharapkan (EV) 60% 8%
Deviasi standar (s atau ) 15% 3%
Koefisien Variasi (CV) 15 = 0.25
60
3 = 0.37
8
0.37 > 0.25 berarti proyek B lebih berisiko
daripada proyek A

32. Contoh Soal:
Jawab :
CVA = $ 231,02 : $ 440
= 0,5250
CVB = $ 406,77 : $ 450
= 0,9039
Maka proyek yang dipilih adalah yang risiko relatifnya
lebih kecil yaitu proyek A dengan koefisien variasi 0,5250
atau 52,5%
Proyek Keuntungan yang
diharapkan (EV)
Standard deviasi
∑
A $ 440 $ 231,02
B $ 450 $ 406,77

33. COVARIANCE

34. COVARIANCE
ADALAH PENGUKUR YANG MENUNJUKKAN ARAH
PERGERAKAN DUA BUAH VARIABEL

35. • Merupakan korelasi antara dua variabel
dikalikan dengan standard deviasi masing-
masing
n
Cov = ∑ (RiA – EVA) (RiB – EVB) x Pri
i=1
Keterangan :
EVA = expected value pada Investasi A
EVB = expected value pada Investasi B
RiA = tingkat keuntungan pada investasi A
RiB = tingkat keuntungan pada investasi B
Pri = probabilitas kondisi i terjadi
COVARIANCE

36. Contoh Soal :
Hitunglah besarnya Covariance kedua investasi diatas dengan
nilai Expected Value sebelumnya:
Wings: EV = 0,165 atau 16,5%
Indofood: EV = 0,15 atau 15%
Keadaan
Ekonomi
Probabilitas
Kejadian
Rate of Return on Stock
PT. A PT. B
Booming 0.3 30% 20%
Normal 0.4 15% 15%
Resesi 0.3 5% 10%

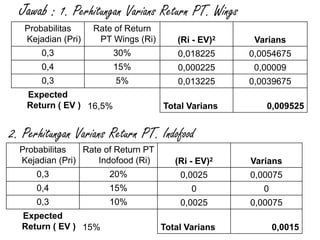
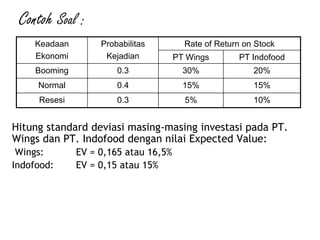
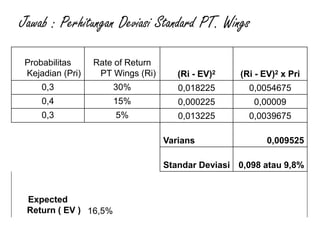
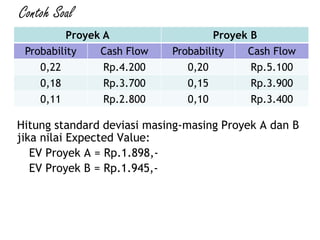
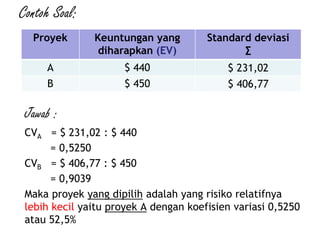
37. Jawab :
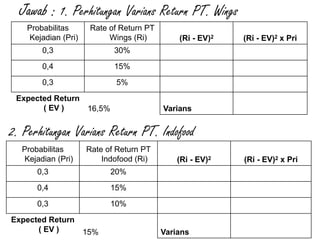
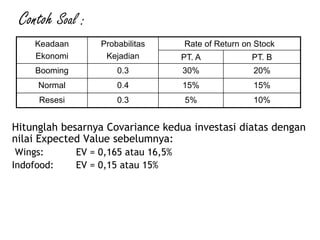
CoVAB= [(0,3 – 0,165).(0,2 - 0,15)]0,3 + [(0,15 - 0,145).
(0,15 - 0,15)]0,4 + [(0,05 – 0,165) . (0,1 – 0,15)] 0,3
= [(0,135x0,05).0,3]+[(0,005x0).0,4]+[(-0,115x-0,05).0,3]
= 0,002025 + 0 + 0,001725
= 0.00375 atau 0,3%
Maka kedua proyek/investasi tersebut memiliki korelasi risiko
sebesar 0,3%

38. Contoh Soal
Hitung Covariance kedua proyek diatas jika nilai
Expected Value:
EV Proyek A = Rp.1.898,-
EV Proyek B = Rp.1.945,-
Proyek A Proyek B
Probability Cash Flow Probability Cash Flow
0,22 Rp.4.200 0,20 Rp.5.100
0,18 Rp.3.700 0,15 Rp.3.900
0,11 Rp.2.800 0,10 Rp.3.400

39. VALUE AT RISK (VaR)

40. Jumlah Kerugian (Value at Risk/VaR)

41. Z score dan Standar Deviasi
Tingkat kepercayaan (%)
 99 ( =1) 97,5 ( =2,5) 95 ( =5) 90 ( =10)
Z score 2,326 1,960 1,645 1,282

42. Contoh Soal
PT Tandun memiliki banyak alat berat, salah satu
diantaranya Crane merk XYZ. Berdasarkan data yang
dimiliki perusahaan, dalam 3 tahun terakhir, Crane
merk XYZ mengalami patah as sebanyak 6 kali dengan
data sbb:
Berapa besar dana yang harus dicadangkan untuk
mengantisipasi kerugian akibat patah as?
Kejadian ke Kerugian (Rupiah)
1 120 jt
2 135 jt
3 110 jt
4 130 jt
5 115 jt
6 100 jt

43. Jawab
Rata-rata kerugian yang ditimbulkan :
Kejadian ke
1 120.000.000 2,79 x 1012
2 135.000.000 277,89 x 1012
3 110.000.000 69,39 x 1012
4 130.000.000 136,19 x 1012
5 115.000.000 11,09 x 1012
6 100.000.000 335,99 x 1012
Total kerugian dalam 3 tahun 710.000.000
833,35 x 1012
118.333.333

44. Besar dana yang harus dicadangkan (VaR) adalah

45. Contoh Soal :
• Suatu perusahaan yang bergerak dibidang penyewaan
mesin genset memiliki data historis dalam 6 tahun
terakhir, mesin mengalami kerusakan sebanyak 6 kali
dengan kerugian untuk setiap kejadian sbb:
• Berapa besar dana yang dicadangkan untuk
mengantisipasi risiko kerugian tersebut tahun depan?
Kejadian Kerugian (Rupiah)
Tahun 1 1.200.000
Tahun 2 1.350.000
Tahun 3 1.100.000
Tahun 4 1.300.000
Tahun 5 1.150.000
Tahun 6 1.000.000

46. Jawab :
Kejadian ke
1 1.200.000 277.788.889
2 1.350.000 27.777.888.890
3 1.100.000 6.944.388.889
4 1.300.000 13.611.188.890
5 1.150.000 1.111.088.889
6 1.000.000 33.610.988.890
Total kerugian dalam 6 tahun 7.100.000
83.333.333.3401.183.333

47. Contoh Soal:
• Terdapat 2 investasi yang akan dipilih dengan data sbb:
• Dengan mempertimbangkan besarnya dana yang akan
dicadangkan untuk mengantisipasi risiko, Manakah
investasi yang Sdr pilih?
Investasi A Investasi B
Nilai Investasi (I) 10 Milyar 12 Milyar
Expected Return (EV) 15% 12%
Standard Deviasi () 18% 15%
Investasi A Investasi B
Nilai Investasi (I) 10 12
Expected Return (EV) 0,15 0,12
Standard Deviasi () 0,18 0,15
Return (x = I.EV) 1,5 1,44
n 1 1

48. Jawab :

49. NEXT
PENDEKATAN KUALITATIF DALAM ANALISIS RISIKO