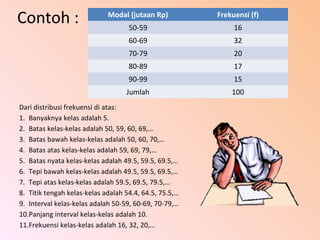
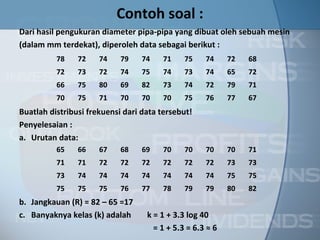
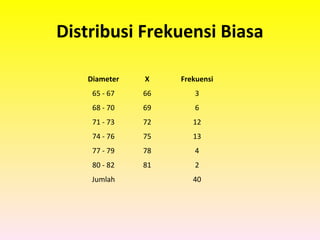
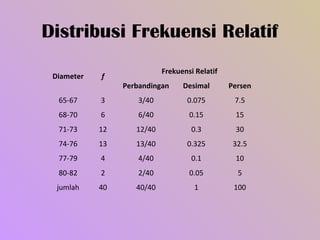
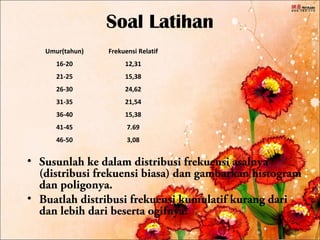
Dokumen ini membahas tentang distribusi frekuensi, termasuk pengertian, bagian-bagian, dan cara penyusunan data dalam bentuk tabel atau grafik. Diterangkan juga jenis-jenis distribusi frekuensi seperti distribusi frekuensi biasa, relatif, dan kumulatif serta teknik pembuatan histogram dan poligon frekuensi. Contoh penggunaan distribusi frekuensi pada data diameter pipa juga disertakan untuk ilustrasi lebih jelas.

1. BAB 2
DISTRIBUSI
FREKUENSI

2. Tujuan Pembelajaran
Mahasiswa mampu:
Melakukan penyajian data dalam bentuk
tabel atau grafik

3. Pengertian
 Susunan data menurut kelas-kelas interval tertentu
atau menurut kategori tertentu dalam sebuah
daftar
 Dari distribusi frekuensi dapat diperoleh
keterangan atau gambaran sederhana dan
sistematis dari data yang diperoleh.

4. Bagian-bagian distribusi frekuensi
• Kelas-kelas (class)
• Batas kelas (class limits)
• Tepi kelas (class boundary)
• Titik tengah kelas/tanda kelas (class mid
point/class marks)
• Interval kelas (class interval)
• Panjang Interval kelas atau kelas (interval kelas)
• Frekuensi kelas (class frequency)

5. Contoh : Modal (jutaan Rp)
50-59
Frekuensi (f)
16
60-69 32
70-79 20
80-89 17
90-99 15
Jumlah 100
Dari distribusi frekuensi di atas:
1. Banyaknya kelas adalah 5.
2. Batas kelas-kelas adalah 50, 59, 60, 69,…
3. Batas bawah kelas-kelas adalah 50, 60, 70,…
4. Batas atas kelas-kelas adalah 59, 69, 79,…
5. Batas nyata kelas-kelas adalah 49.5, 59.5, 69.5,…
6. Tepi bawah kelas-kelas adalah 49.5, 59.5, 69.5,…
7. Tepi atas kelas-kelas adalah 59.5, 69.5, 79.5,…
8. Titik tengah kelas-kelas adalah 54.4, 64.5, 75.5,…
9. Interval kelas-kelas adalah 50-59, 60-69, 70-79,…
10.Panjang interval kelas-kelas adalah 10.
11.Frekuensi kelas-kelas adalah 16, 32, 20,…

6. Penyusunan Distribusi
Frekuensi
1. Mengurutkan data dari yang terkecil ke yang terbesar.
2. Menentukan jangkauan (range) dari data.
Jangkauan = data terbesar – data terkecil
3. Menentukan banyaknya kelas (k).
k = 1 + 3.3 log n; k Є bulat
ket : k = banyaknya kelas
n = banyaknya data
Hasil dibulatkan, biasanya ke atas.
4. Menentukan panjang interval kelas.
Panjang interval kelas (i) = jangkauan (R) / banyaknya kelas (k)
5. Menentukan batas bawah kelas pertama.
6. Menuliskan frekuensi kelas secara melidi dalam kolom turus sesuai
banyaknya data.

7. Contoh soal :
Dari hasil pengukuran diameter pipa-pipa yang dibuat oleh sebuah mesin
(dalam mm terdekat), diperoleh data sebagai berikut :
78 72 74 79 74 71 75 74 72 68
72 73 72 74 75 74 73 74 65 72
66 75 80 69 82 73 74 72 79 71
70 75 71 70 70 70 75 76 77 67
Buatlah distribusi frekuensi dari data tersebut!
Penyelesaian :
a. Urutan data:
65 66 67 68 69 70 70 70 70 71
71 71 72 72 72 72 72 72 73 73
73 74 74 74 74 74 74 74 75 75
75 75 75 76 77 78 79 79 80 82
b. Jangkauan (R) = 82 – 65 =17
c. Banyaknya kelas (k) adalah k = 1 + 3.3 log 40
= 1 + 5.3 = 6.3 ≈ 6

8. Histogram, Poligon, Frekuensi, dan
Kurva
Histogram dan Poligon Frekuensi
• Histogram dan poigon frekuensi adalah dua grafik yang sering
digunakan
untuk menggambarkan distribusi frekuensi.
• Histogram merupakan grafik batang dari distribusi frekuensi dan
poligon frekuensi merupakan grafik garisnya.
• Batang-batang pada histogram saling melekat atau berimpitan.
• Poligon frekuensi dibuat dengan cara menarik garis dari satu titik
tengah batang histogram ke titiktengah batang histogram yang
lain.
• Pada pembuatan histogram digunakan sistem salin sumbu.
Sumbu-sumbu mendatar (sumbu X) menyatakan interval kelas
(tepi bawah kelas dan tepi atas masing-masing kelas) dan sumbu
tegak (sumbu Y) menyatakan frekuensi.

9. d. Panjang interval kelas (i) adalah
i = 17/6 =2.8 ≈ 3
e. Batas kelas pertama adalah 65 (data terkecil)
f. Tabel :
Diameter Turus Frekuensi
65 – 67 III 3
68 – 70 IIIII I 6
71 – 73 IIIII IIIII II 12
74 – 76 IIIII IIIII III 13
77 – 79 IIII 4
80 – 82 II 2
Jumlah 40

10. Histogram, Poligon, Frekuensi, dan
Kurva
Bentuk Kurva Frekuensi
• Simetris atau berbentuk lonceng, ciri-cirinya ialah
nilai variabel di samping kiri dan kanan yang
berjarak sama terhadap titik tengah (frekuensi
terbesar) mempunyai frekuensi yang sama.
Dinamakan juga distribusi normal.
• Tidak simetris/condong. Condong ke kanan
(kocondongan positif) , Condong ke kiri
(kecondongan negatif).

11. Histogram, Poligon, Frekuensi, dan
Kurva
Bentuk Kurva Frekuensi
• Bentuk J atau J terbalik, ciri-cirinya ialah salah satu
nilai ujung kurva memiliki frekuensi maksimum.
• Bentuk U, dengan ciri kedua ujung kurva memiliki
frekuensi maksimum.
• Bimodal, dengan ciri mempunyai dua maksimal.
• Multimodal, dengan ciri mempunyai lebih dari dua
maksimal.
• Uniform, terjadi bila nilai-nilai variabel dalam suatu
interval mempunyai frekuensi yang sama.

12. Jenis-jenis Distribusi Frekuensi
Distribusi Frekuensi Biasa
adalah distribusi frekuensi ysng hanya berisikan jumlah
frekuensi dari setiap kelompok data atau kelas.
Jenis DFB:
 Distribusi Frekuensi Numerik
adalah distribusi frekuensi yang pembagian kelasnya
dinyatakan dalam angka.
Contoh : Tabel Frekuensi pelamar suatu perusahaan
berdasarkan umur.
 Distribusi Frekuensi Peristiwa atau kategori
adalah yang pembagian kelasnya dinyatakan berdasarkan
data atau golongan data yang ada.
Contoh : Tabel banyaknya peristiwa pada hasil pelemparan
dadu berdasarkan anga dadu.

13. Jenis-jenis Distribusi Frekuensi
• Distribusi Frekuensi Relatif
adalah distribusi frekuensi yang berisikan nilai-
nilai hasil bagi antara frekuensi kelas dan
jumlah pengamatan yang terkandung dalam
kumpulan data yang terdistribusi tertentu.
Rumus :

14. Contoh DFR
Frekuensi relatif dapat dinyatakan dalam
bentuk perbandingan, desimal atau persen.
Interval Kelas f Frekuensi Relatif
(Tinggi (cm)) (Banyak Murid) Perbandingan Desimal Persen
140-144 2 2/50 0.04 4
145-149 4 4/50 0.08 8
150-154 10 10/50 0.2 20
155-159 14 14/50 0.28 28
160-164 12 12/50 0.24 24
165-169 5 5/50 0.1 10
170-174 3 3/50 0.06 6
Jumlah 50 1 1 100

15. Jenis-jenis Distribusi Frekuensi
Distribusi Frekuensi Kumulatif
Adalah distribusi frekuensi yang berisikan frekuensi
kumulatif.
Frekuensi kumulatif adalah frekuensi yang dijumlahkan.
Distribusi frekuensi kumulatif memiliki grafik atau kurva
yang disebut ogif.
Jenis DFK
 Distribusi Frekuensi Kumulatif Kurang Dari
adalah distribusi frekuensi yang memuat jumlah frekuensi yang
memiliki nilai kurang dari nilai batas kelas suatu interval tertentu.
 Distribusi Frekuensi Kumulatif Lebih Dari
adalah distribusi frekuensi yang memuat jumlah frekuensi yang
memiliki nilai lebih dari nilai batas kelas suatu interval tertentu.

16. Contoh
Berikut ini adalah mid point dari pengukuran 40
diameter pipa-pipa beserta frekuensinya.
Diameter X Frekuensi
65 - 67 66 3
68 - 70 69 6
71 - 73 72 12
74 - 76 75 13
77 - 79 78 4
80 - 82 81 2
• Susunlah mid point tersebut ke dalam distribusi frekuensi
biasa dan gambarkan histogram dan poligonnya!
• Buatlah distribusi frekuensi relatif!
• Buatlah distribusi frekuensi kumulatif kurang dari dan lebih
dari serta gambarkan ogifnya masing-masing

17. Penyelesaian batas atas dan bawah

19. Distribusi Frekuensi Biasa
Diameter X Frekuensi
65 - 67 66 3
68 - 70 69 6
71 - 73 72 12
74 - 76 75 13
77 - 79 78 4
80 - 82 81 2
Jumlah 40

20. Perhitungan Frekuensi Relatif

21. Distribusi Frekuensi Relatif
Frekuensi Relatif
Diameter f
Perbandingan Desimal Persen
65-67 3 3/40 0.075 7.5
68-70 6 6/40 0.15 15
71-73 12 12/40 0.3 30
74-76 13 13/40 0.325 32.5
77-79 4 4/40 0.1 10
80-82 2 2/40 0.05 5
jumlah 40 40/40 1 100

22. Soal Latihan
Umur(tahun) Frekuensi Relatif
16-20 12,31
21-25 15,38
26-30 24,62
31-35 21,54
36-40 15,38
41-45 7.69
46-50 3,08
• Susunlah ke dalam distribusi frekuensi asalnya
(distribusi frekuensi biasa) dan gambarkan histogram
dan poligonya.
• Buatlah distribusi frekuensi kumulatif kurang dari
dan lebih dari beserta ogifnya!