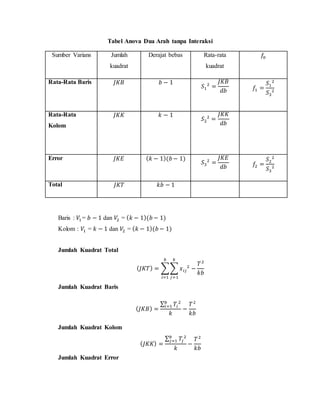
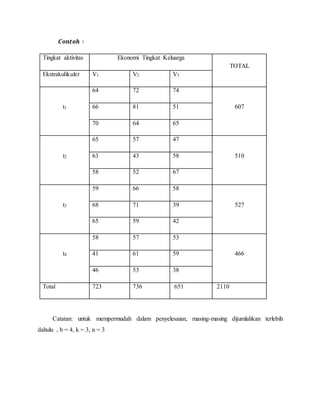
1) Analisis varian dua arah digunakan untuk mengetahui pengaruh dua kriteria terhadap hasil yang diinginkan;
2) Metode ini membandingkan rata-rata dari beberapa kategori untuk satu variabel perlakuan serta memperluas analisis pada situasi dimana hal yang diukur dipengaruhi oleh dua faktor;
3) Terdapat dua jenis analisis varian dua arah, yaitu tanpa interaksi dan dengan interaksi antar faktor.