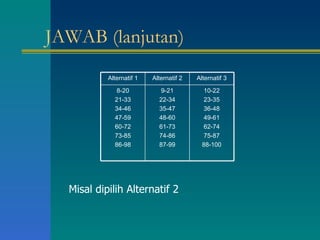
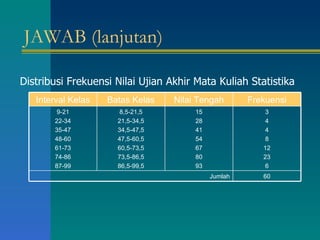
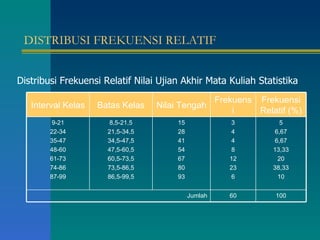
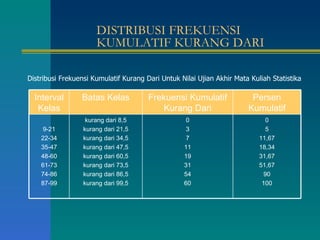
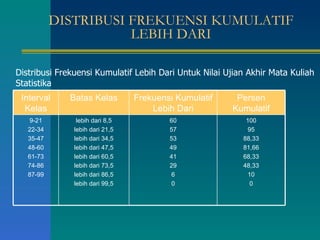
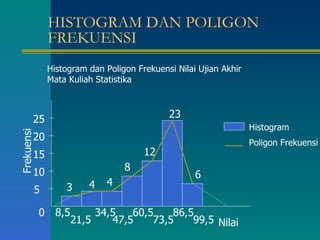
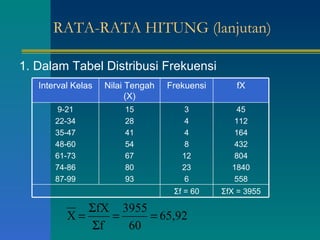
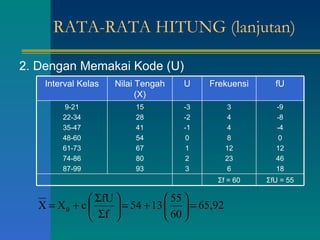
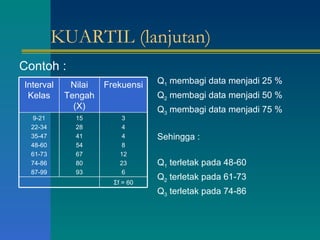
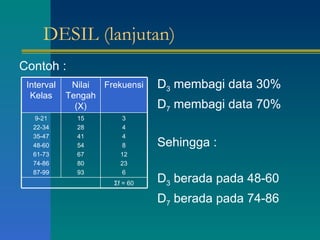
Dokumen tersebut memberikan penjelasan tentang daftar distribusi frekuensi yang disusun oleh beberapa mahasiswa. Terdapat contoh distribusi frekuensi tinggi badan 100 mahasiswa beserta penjelasan tentang batas kelas, nilai tengah, dan cara membuat tabel distribusi frekuensi. Dokumen ini juga menjelaskan tentang distribusi frekuensi relatif dan kumulatif serta ukuran pemusatan data seperti rata-rata, median, dan modus.

1. STATISTIK DAFTAR DISTRIBUSI FREKUENSI DISUSUN OLEH : NAMA : MHD.ANWAR SIMATUPANG MHD. FURQAN KHAIRUL INDRA ZULFIKAR HARYOSANA

2. DEFINISI Pengelompokkan data menjadi tabulasi data dengan memakai kelas-kelas data dan dikaitkan dengan masing-masing frekuensinya BAB I DAFTAR DISTRIBUSI FREKUENSI

3. KELEBIHAN DAN KEKURANGAN Kelebihan Dapat mengetahui gambaran secara menyeluruh Kekurangan Rincian atau informasi awal menjadi hilang

4. CONTOH Distribusi Frekuensi Tinggi Badan 100 Mahasiswa UNIMED Sumber: Data buatan Tinggi Badan Frekuensi 151-153 154-156 157-159 160-162 163-165 166-168 169-171 172-174 3 7 12 18 27 17 11 5

5. LIMIT, BATAS, NILAI TENGAH, DAN LEBAR KELAS Limit Kelas/Tepi Kelas Nilai terkecil/terbesar pada setiap kelas Batas Kelas Nilai yang besarnya satu desimal lebih sedikit dari data aslinya Nilai Tengah Kelas Nilai tengah antara batas bawah kelas dengan batas atas kelas Lebar Kelas Selisih antara batas bawah kelas dengan batas atas kelas

6. CARA MEMBUAT TABEL DISTRIBUSI FREKUENSI Tentukan Range atau jangkauan data (r) Tentukan banyak kelas (k) Rumus Sturgess : k=1+3,3 log n Tentukan lebar kelas (c) c=r/k

7. CARA MEMBUAT TABEL DISTRIBUSI FREKUENSI (lanjutan) Tentukan limit bawah kelas pertama dan kemudian batas bawah kelasnya Tambah batas bawah kelas pertama dengan lebar kelas untuk memperoleh batas atas kelas Tentukan limit atas kelas Tentukan nilai tengah kelas Tentukan frekuensi

8. CONTOH Data hasil ujian akhir Mata Kuliah Statistika dari 60 orang mahasiswa 23 60 79 32 57 74 52 70 82 36 80 77 81 95 41 65 92 85 55 76 52 10 64 75 78 25 80 98 81 67 41 71 83 54 64 72 88 62 74 43 60 78 89 76 84 48 84 90 15 79 34 67 17 82 69 74 63 80 85 61

9. JAWAB Data terkecil = 10 dan Data terbesar = 98 r = 98 – 10 = 88 Jadi jangkauannya adalah sebesar 88 Banyak kelas (k) = 1 + 3,3 log 60 = 6,8 Jadi banyak kelas adalah sebanyak 7 kelas Lebar kelas (c) = 88 / 7 = 12,5 mendekati 13 Limit bawah kelas pertama adalah 10, dibuat beberapa alternatif limit bawah kelas yaitu 10, 9, dan 8 Maka batas bawah kelas-nya adalah 9,5 ; 8,5 ; dan 7,5

10. JAWAB (lanjutan) Batas atas kelas pertama adalah batas bawah kelas ditambah lebar kelas, yaitu sebesar - 9,5 + 13 = 22,5 - 8,5 + 13 = 21,5 - 7,5 + 13 = 20,5 Limit atas kelas pertama adalah sebesar - 22,5 - 0,5 = 22 - 21,5 - 0,5 = 21 - 20,5 – 0,5 = 20

11. JAWAB (lanjutan) Misal dipilih Alternatif 2 Alternatif 1 Alternatif 2 Alternatif 3 8-20 21-33 34-46 47-59 60-72 73-85 86-98 9-21 22-34 35-47 48-60 61-73 74-86 87-99 10-22 23-35 36-48 49-61 62-74 75-87 88-100

12. JAWAB (lanjutan) Nilai tengah kelas adalah Frekuensi kelas pertama adalah 3

13. JAWAB (lanjutan) Distribusi Frekuensi Nilai Ujian Akhir Mata Kuliah Statistika Interval Kelas Batas Kelas Nilai Tengah Frekuensi 9-21 22-34 35-47 48-60 61-73 74-86 87-99 8,5-21,5 21,5-34,5 34,5-47,5 47,5-60,5 60,5-73,5 73,5-86,5 86,5-99,5 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Jumlah 60

14. DISTRIBUSI FREKUENSI RELATIF DAN KUMULATIF Distribusi frekuensi relatif Membandingkan frekuensi masing-masing kelas dengan jumlah frekuensi total dikalikan 100 % Distribusi frekuensi kumulatif ada 2, yaitu distribusi frekuensi kumulatif kurang dari dan lebih dari

15. DISTRIBUSI FREKUENSI RELATIF Distribusi Frekuensi Relatif Nilai Ujian Akhir Mata Kuliah Statistika Interval Kelas Batas Kelas Nilai Tengah Frekuensi Frekuensi Relatif (%) 9-21 22-34 35-47 48-60 61-73 74-86 87-99 8,5-21,5 21,5-34,5 34,5-47,5 47,5-60,5 60,5-73,5 73,5-86,5 86,5-99,5 15 28 41 54 67 80 93 3 4 4 8 12 23 6 5 6,67 6,67 13,33 20 38,33 10 Jumlah 60 100

16. DISTRIBUSI FREKUENSI KUMULATIF KURANG DARI Distribusi Frekuensi Kumulatif Kurang Dari Untuk Nilai Ujian Akhir Mata Kuliah Statistika Interval Kelas Batas Kelas Frekuensi Kumulatif Kurang Dari Persen Kumulatif 9-21 22-34 35-47 48-60 61-73 74-86 87-99 kurang dari 8,5 kurang dari 21,5 kurang dari 34,5 kurang dari 47,5 kurang dari 60,5 kurang dari 73,5 kurang dari 86,5 kurang dari 99,5 0 3 7 11 19 31 54 60 0 5 11,67 18,34 31,67 51,67 90 100

17. DISTRIBUSI FREKUENSI KUMULATIF LEBIH DARI Distribusi Frekuensi Kumulatif Lebih Dari Untuk Nilai Ujian Akhir Mata Kuliah Statistika Interval Kelas Batas Kelas Frekuensi Kumulatif Lebih Dari Persen Kumulatif 9-21 22-34 35-47 48-60 61-73 74-86 87-99 lebih dari 8,5 lebih dari 21,5 lebih dari 34,5 lebih dari 47,5 lebih dari 60,5 lebih dari 73,5 lebih dari 86,5 lebih dari 99,5 60 57 53 49 41 29 6 0 100 95 88,33 81,66 68,33 48,33 10 0

18. HISTOGRAM DAN POLIGON FREKUENSI 0 5 10 15 20 25 Frekuensi 8,5 21,5 34,5 47,5 60,5 73,5 86,5 99,5 3 4 4 8 12 23 6 Nilai Histogram Poligon Frekuensi Histogram dan Poligon Frekuensi Nilai Ujian Akhir Mata Kuliah Statistika

19. UKURAN PEMUSATAN DAN LETAK DATA BAB II

20. UKURAN PEMUSATAN Merupakan nilai tunggal yang mewakili semua data atau kumpulan pengamatan dimana nilai tersebut menunjukkan pusat data. Yang termasuk ukuran pemusatan : Rata-rata hitung Median Modus Rata-rata ukur Rata-rata harmonis

21. 1. RATA-RATA HITUNG Rumus umumnya : Untuk data yang tidak mengulang Untuk data yang mengulang dengan frekuensi tertentu

22. RATA-RATA HITUNG (lanjutan) 1. Dalam Tabel Distribusi Frekuensi Interval Kelas Nilai Tengah (X) Frekuensi fX 9-21 22-34 35-47 48-60 61-73 74-86 87-99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 45 112 164 432 804 1840 558 Σf = 60 ΣfX = 3955

23. RATA-RATA HITUNG (lanjutan) 2. Dengan Memakai Kode (U) Interval Kelas Nilai Tengah (X) U Frekuensi fU 9-21 22-34 35-47 48-60 61-73 74-86 87-99 15 28 41 54 67 80 93 -3 -2 -1 0 1 2 3 3 4 4 8 12 23 6 -9 -8 -4 0 12 46 18 Σf = 60 ΣfU = 55

24. RATA-RATA HITUNG (lanjutan) 3. Dengan pembobotan Masing-masing data diberi bobot. Misal A memperoleh nilai 65 untuk tugas, 76 untuk mid dan 70 untuk ujian akhir. Bila nilai tugas diberi bobot 2, Mid 3 dan Ujian Akhir 4, maka rata-rata hitungnya adalah :

25. 2. MEDIAN Untuk data berkelompok

26. MEDIAN (lanjutan) Contoh : Letak median ada pada data ke 30, yaitu pada interval 61-73, sehingga : L 0 = 60,5 F = 19 f = 12 Interval Kelas Frekuensi 9-21 22-34 35-47 48-60 61-73 74-86 87-99 3 4 4 8 12 23 6 Σf = 60

27. 3. MODUS Untuk data berkelompok

28. MODUS (lanjutan) Contoh : Data yang paling sering muncul adalah pada interval 74-86, sehingga : L 0 = 73,5 b 1 = 23-12 = 11 b 2 = 23-6 =17 Interval Kelas Frekuensi 9-21 22-34 35-47 48-60 61-73 74-86 87-99 3 4 4 8 12 23 6 Σf = 60

29. HUBUNGAN EMPIRIS ANTARA NILAI RATA-RATA HITUNG, MEDIAN, DAN MODUS Ada 3 kemungkinan kesimetrian kurva distribusi data : Jika nilai ketiganya hampir sama maka kurva mendekati simetri. Jika Mod<Med<rata-rata hitung, maka kurva miring ke kanan. Jika rata-rata hitung<Med<Mod, maka kurva miring ke kiri.

30. KUARTIL, DESIL, PERSENTIL 1. Kuartil Kelompok data yang sudah diurutkan (membesar atau mengecil) dibagi empat bagian yang sama besar. Ada 3 jenis yaitu kuartil pertama (Q 1 ) atau kuartil bawah, kuartil kedua (Q 2 ) atau kuartil tengah, dan kuartil ketiga (Q 3 ) atau kuartil atas.

31. KUARTIL (lanjutan) Untuk data tidak berkelompok Untuk data berkelompok L 0 = batas bawah kelas kuartil F = jumlah frekuensi semua kelas sebelum kelas kuartil Q i f = frekuensi kelas kuartil Q i

32. KUARTIL (lanjutan) Contoh : Q 1 membagi data menjadi 25 % Q 2 membagi data menjadi 50 % Q 3 membagi data menjadi 75 % Sehingga : Q 1 terletak pada 48-60 Q 2 terletak pada 61-73 Q 3 terletak pada 74-86 Interval Kelas Nilai Tengah (X) Frekuensi 9-21 22-34 35-47 48-60 61-73 74-86 87-99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Σf = 60

33. KUARTIL (lanjutan) Untuk Q 1 , maka : Untuk Q 2 , maka : Untuk Q 3 , maka :

34. KUARTIL, DESIL, PERSENTIL (lanjutan) 2. Desil Kelompok data yang sudah diurutkan (membesar atau mengecil) dibagi sepuluh bagian yang sama besar.

35. DESIL (lanjutan) Untuk data tidak berkelompok Untuk data berkelompok L 0 = batas bawah kelas desil D i F = jumlah frekuensi semua kelas sebelum kelas desil D i f = frekuensi kelas desil D i

36. DESIL (lanjutan) Contoh : D 3 membagi data 30% D 7 membagi data 70% Sehingga : D 3 berada pada 48-60 D 7 berada pada 74-86 Interval Kelas Nilai Tengah (X) Frekuensi 9-21 22-34 35-47 48-60 61-73 74-86 87-99 15 28 41 54 67 80 93 3 4 4 8 12 23 6 Σf = 60

37. DESIL (lanjutan)

38. KUARTIL, DESIL, PERSENTIL (lanjutan) 3. Persentil Untuk data tidak berkelompok Untuk data berkelompok

39. D 3 = 47,5 + 13 3 x 60 100 8 - - -11 = D 7= 73,5 + 13 7 x 60 100 23 - -31 = 58,35 32,55

40. KESIMPULAN Dari penyelesaian soal-soal diatas maka dapat disimpulkan bahwa: Nilai rata-rata hitungnya = 65,92 (berbagai cara) Median dari data tersebut yaitu 72,42 Modus dari data tersebut yaitu 78,61 Nilai dari kuartil 1 = 54 Nilai dari kuartil 2 = 72,42 Nilai dari kuartil 3 = 81,41 Nilai desil 3 = 58,875 Nilai desil 7 = 79,72 Sedangakan nilai persentil 3 = 32,55 Dan nilai persentil 7 =58,35

41. KESIMPULAN JADI UNTUK MEMBUAT SUATU DAFTAR DISRIBUSI FREKUENSI HASIL SESUAI DENGAN RUMUS UNTUK MENDAPATKAN HASIL YANG AKURAT. Interval Kelas Nilai Tengah (X) 9-21 22-34 35-47 48-60 61-73 74-86 87-99 DLL 15 28 41 54 67 80 93 DLL

42. TERIMA KASIH