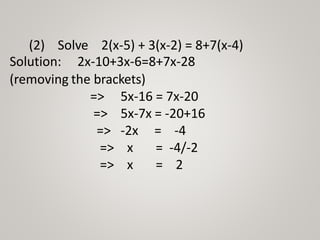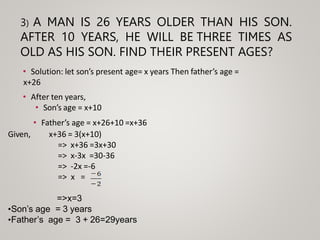The document defines and discusses linear equations in one variable. It begins by defining an equation as a statement that two algebraic expressions are equal. It then defines a linear equation in one variable as an equation involving only one variable of the first degree. The document goes on to list properties of equations and methods for solving different types of linear equations in one variable, including using addition/subtraction, multiplication/division, and transposing terms. It also provides examples of solving word problems involving linear equations.

1. LINEAR EQUATION IN
ONE VARIABLE
Prepared by:
SHARDA CHAUHAN
TGT MATHEMATICS

2. A statement which states that two algebraic expressions are equal is called
an equation.
3x  2y  8
6  x  x  9
3X2
 5  X 
5
The equation involving only one variable in first order is called a linear
equation in one variable.
3x50
8y 2
7a153a

3. PROPERTIES OF AN EQUATION
•If same quantity is added to both sides of the equation,
the sums are equal.
Thus: x=7 => x+a=7+a
•If same quantity is subtracted from both sides of an
equation, the differences are equal
Thus: x=7 => x-a=7-a
•If both the sides of an equation are multiplied by the
same quantity, the products are equal.
Thus: x=7 => ax=7a
•If both the sides of an equation are divided by the same
quantity, the quotients are equal.
Thus: x=7 => x÷a=7÷a

4. TO SOLVE AN EQUATION
1.To solve an equation of the form x+a=b
=> x+4-4=10-4 (subtracting 4 from both the
E.g.: Solve x+4=10
Solution: x+4=10
sides)
=> x=6
2.To solve an equation of the form x-a=b
E.g.: Solve y-6=5 equal.
Solution: y-6=5 (adding 6 to both sides)
=> y-6+6=5+6
=> y=11

5. 3.TO SOLVE AN EQUATION OF THE
FORM AX=B
E.G.: SOLVE
3X=9
SOLUTION: 3X=9
4. To solve an equation of the form x/a=b
E.g.: Solve = 6
Solution: ×=6×2
3
=> x =
x
2
=> x=12

6. SHORT- CUT METHOD (SOLVING AN
EQUATION BY TRANSPOSING TERMS)
1.In an equation, an added term is transposed (taken) from one side to the
other, it is subtracted.
i.e., x+4=10
=> x=10-4=6 (4 is transposed)
2. In an equation, a subtracted term is transposed to the other side, it is added.
i.e., y-6=5
=>y=5+6=11
3. In an equation, a term in multiplication is transposed to the other side, it is
divided.
i.e., 3x=12
=>x=12/3=4
4. In an equation a term in division is taken to the other side it is multiplied.
i.e
=> y=6×4=24 (4 is transposed)
x
(6 is transposed)
(3 is transposed)

7. TO SOLVE EQUATIONS USING MORE THAN ONE
PROPERTY
Solve: (1) 3x+8=14
Solution: (transposing 8)
3x=14-8
=> 3x=6
=> x=6/3 (transposing 3)
=>x=2

8. (2)2A-3=5
Solution: (transposing 3)
(transposing2)
2a=5+3
=> 2a=8
=> a = 8/2
=> a = 4

9. (3) 5N/8 =20
Solution: 5n=20×8
=> n =204×8/51
=> n=4×8=32

10. SOL
VINGANEQUA
TIONWITHV
ARIABLEON
BOTHTHESIDES
Transpose the terms containing the variable, to one
side and the constants to the other side
.
E.g.: (1) Solve 10y-3=7y+9
Solution: 10y-7y = 9+3 (transposing 7y to the
left & 3 to the right)
=> 3y = 12
=> y = 12/3
=> y = 4

11. (2) Solve 2(x-5) + 3(x-2) = 8+7(x-4)
Solution: 2x-10+3x-6=8+7x-28
(removing the brackets)
=> 5x-16 = 7x-20
=> 5x-7x = -20+16
=>
=>
=>
-2x = -4
x = -4/-2
x = 2

12. SOLVING WORD PROBLEMS
•A number increased by 8 equal 15. Find
the number?
Solution: Let the number be ‘x’
Given, the number increased by 8 equal 15.
=> x+8 = 15
=> x = 15-8
=> x = 7

13. •A number is decreased by 15 and the new number
so obtained is multiplied by 3; the result is 81.Find
the number?
Solution: Let the number be ‘x’
The number decreased by 15 = x-15
The new number (x-15) multiplied by 3 = 3(x-15)
Given 3(x-15) = 81
=> 3x-45 = 81
=> 3x = 81 + 45
=> 3x = 126
=> x
3
=> x = 42
= 126

14. 3) A MAN IS 26 YEARS OLDER THAN HIS SON.
AFTER 10 YEARS, HE WILL BE THREE TIMES AS
OLD AS HIS SON. FIND THEIR PRESENT AGES?
• Solution: let son’s present age= x years Then father’s age =
x+26
• After ten years,
• Son’s age = x+10
• Father’s age = x+26+10 =x+36
Given, x+36 = 3(x+10)
=> x+36 =3x+30
=> x-3x =30-36
=> -2x =-6
=> x =
=>x=3
•Son’s age = 3 years
•Father’s age = 3 + 26=29years

15. Any Questions?
ASK!