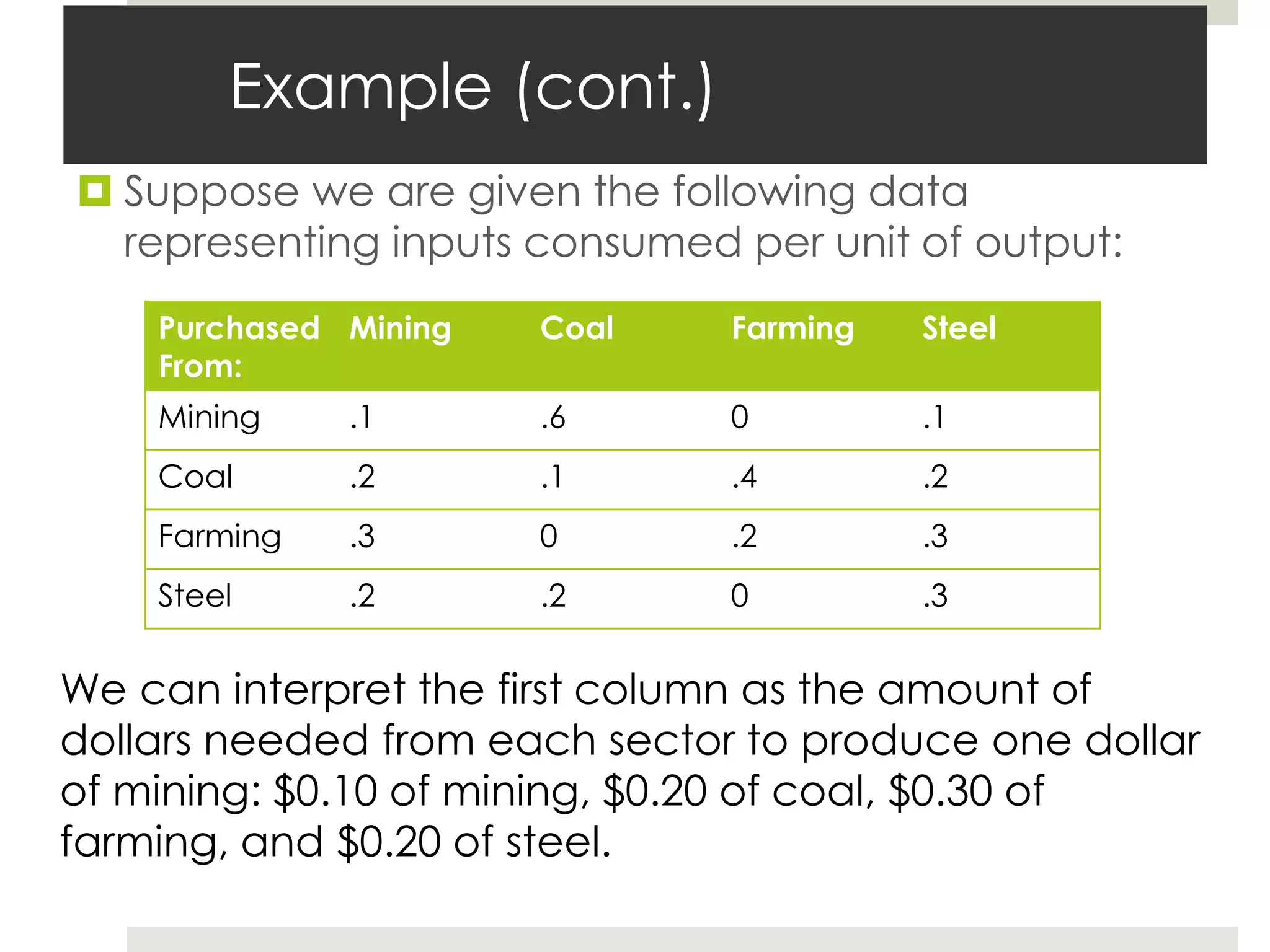
The document summarizes Wassily Leontief's input-output model, which represents interrelationships between economic sectors. It defines sectors as areas of the economy with similar products/services. Leontief divided the US economy into 500 sectors. The model aims to equalize production and demand using matrix algebra. It can be formulated as an open model, which includes external demand, or closed, which ignores demand. The consumption matrix represents input needs per unit of output. Unique solutions for production can be found by manipulating the model's equation. Examples demonstrate applying the open and closed models.

1. Leontief’s Input-Output Model
Ashley Carter
MA 405
Section 002

2. Input-Output Model
 Definition. Leontief’s Input-Output Model is a
representation in modern economic theory that
exemplifies the interrelationship between various
sectors, or industries, of the economy; the model
consists of n sectors producing n products
(“Application to economics”)
 Definition. A sector is an area of the economy in
which different corporations share a similar product
or service (“Sector”)

3. Wassily Leontief
(August, 1906 – Feb., 1999)
 American economist with
citizenship in the Soviet Union and
the United States
 Nobel Prize Winner for the input-
output model in 1973
 Divided economy into 500 industries
for the purpose of his work
 Professor at Harvard
 Created and Managed the Institute
for Economic Analysis at New York
University
(“Wassily Leontief”)

4. Goals of the Model
 Equalize the total amount of goods produced and
the total demand for the good being produced
 Ensure no goods go unused
 Make economic predictions
 Can be adjusted to different settings depending
on the amount of economic sectors involved
(Rincon)

5. Linear Algebra Concepts We Will Use
 Matrix Arithmetic (See 1.3)
 Identity Matrix
 Reduced Row Echelon Form (See 1.2)
 Matrix Augmentation (See 1.1)
 Nonnegative Matrices (See 6.8)
(Chapters and Sections coincide with the Linear Algebra: Eighth
Edition by Steven Leon)

6. Nonnegative Matrices
 Definition. An nxn matrix A with real entries is said to
be nonnnegative if aij ≥ 0 for each i and j and
positive if aij > 0 for each i and j.
 Similary, a vector x = (x1 , x2 , . . . , xn)T is said to be
nonegative if each xi ≥ 0 and positive if each xi > 0.
 Leontief’s Input-Output Models are an applications
of nonnegative matrices.
 It does not make sense for a sector to produce negative
output.
(Leon)

7. Two Types of Models
 Open Model
 The open model assumes that each sector must produce
enough output to meet no only the input requirements of
other industries but also the market demand.
 Closed Model
 The closed model assumes that each sector must produce
enough output to meet the input requirements of only the
other industries and itself, and thus, the market demand is
ignored.
(Leon)

8. Consumption Matrix
 The Consumption Matrix C is an nxn matrix that
represents the units of input needed per unit of
output.
 Entry cij represents the output required from
sector i in ordered to produce one unit of
output in sector j.
(Daddel)

9. Production and Demand
Vectors
 The Production Vector x represents the output
produced by the sectors. Suppose there are n sectors.
Then x = [x1 , x2 , . . . , xn]T. And xi would represent units
of output of sector i.
 The Final Demand Vector d represents the value of
goods or services demanded. Assume there are still n
sectors. Then,
d = [d1 , d2 , . . . , dn]T. And di represents the demand for
output from sector i. (barnyard.syr.edu)

10. The Input-Output Model’s Equation
 Using the consumption matrix C, the final demand
vector d, and the production vector p, the following
equation can be utilized:
p = Cp + d
 For the closed model, d would be equal to 0. Thus, p
= Cp. For now, we will focus on the open model and
return to the closed model later.
(mavdisk.mnsu.edu)

11. Solving the Open Model Equation
 Suppose we have constructed our consumption matrix C and
we know the demand d. Then we can solve for how much
output we need to satisfy the demand
p = Cp + d Ip = Cp + d Ip – Cp = d
( I – C )p = d
 We can augment the matrix ( I – C ) with our demand vector
d, such that we create (( I – C )|d)
 Now we can find the reduced row echelon form of
(( I – C )|d) to find the amount of production needed to satisfy
the demand d.
(Rincon)

12. Open Model Conditions
 The entries of C have two important properties:
(i) cij ≥ 0 for each i and j. Hence C is a
nonnegative matrix.
(ii) cj 1 = Σ cij < 1 for each j.
(Note: 1 denotes the 1-norm, or the matrix norm.)
(Daddel)
n
i = 1

13. Unique Nonnegative Solution for
the Open Model
 We want to show that (I – C)p = d has a unique
nonnegative solution.
 To do so, we need to know, for any mxn matrix B,
 We also need to know that the 1-norm satisfies the following
multiplicative properties:
(Leon)
(1)
(2)

14. Unique Nonnegative Solution for
the Open Model (cont.)
 If the consumption matrix C is an nxn matrix satisfying
both properties (i) and (ii), then it follows from (1) that
C 1 < 1. Furthermore, if λ is any eigenvalue of C and x is
an eigenvector belonging to λ, then
And thus,
 Therefore, 1 is not an eigenvalue of C. It follows that I
– C is nonsingular. Therefore, the system has the unique
solution p = (I – C)-1 d.
(Leon)

15. Unique Nonnegative Solution for the
Open Model (cont.)
Now we need to show that the solution p = (I – C)-1 d is
nonnegative. To do so, we will show (I – C)-1 is
nonnegative. Recall the multiplicative property (2)
introduced on a previous slide. From this, we can say
Since C 1 < 1, it follows that Cm
1 0 as m ∞ and
thus, Cm approaches the zero matrix as m approaches
infinity because
(I – C)(I + C + . . . + Cm) = I – Cm+1 (Leon)

16. Unique Nonnegative Solution for the
Open Model (cont.)
It follows that
I + C + . . . + Cm = (I – C)-1 – (I – C)-1 Cm+1
As m ∞,
(I – C)-1 – (I – C)-1 Cm+1 (I – C)-1
and thus, the series I + C + . . . + Cm converges to (I – C)-1
as m ∞. By property (i), the series is nonnegative for
each m, and thus, (I – C)-1 is nonnegative. Since d and (I
– C)-1 are both nonnegative, p must be nonnegative.
(Leon)

17. Example of the Open Model
 Suppose we have four sectors: mining, coal,
farming, and steel. Thus, in this case, the
consumption matrix will be a 4x4 matrix. The
production vector and demand vector will both be
4x1 matrices.
 Let our demand mining, coal, farming, and steel be
70, 50, 80, and 40 respectively. Then, we can create
the demand vector d:
d = (70, 50, 80, 40)T

18. Example (cont.)
 Suppose we are given the following data
representing inputs consumed per unit of output:
Purchased
From:
Mining Coal Farming Steel
Mining .1 .6 0 .1
Coal .2 .1 .4 .2
Farming .3 0 .2 .3
Steel .2 .2 0 .3
We can interpret the first column as the amount of
dollars needed from each sector to produce one dollar
of mining: $0.10 of mining, $0.20 of coal, $0.30 of
farming, and $0.20 of steel.

19. Example (cont.)
 We can now construct our consumption matrix.
Let C =
Then (I – C) =

20. Example (cont.)
 Now, we can create the augmented matrix ((I – C)|d):
Therefore, p = (313, 312, 306, 236)T.
(Values have been rounded to the nearest whole number.)
rref

21. Example (cont.)
 We used Reduced Row Echelon Form to solve for p
using the augmented matrix ((I – C)|d).
 We could have solved for p by multiplying the
matrices (I – C)-1 and d.
 Both ways yield the same result.
p = (I – C)-1 d = (313, 312, 306, 236)T
 The solution p can be interpreted as follows: the
sectors mining, coal, farming, and steel should
respectively produce $313, $312, $306, and $236 of
their products to meets their respective demands.

22. Closed Input-Output Model
 Total output from the jth industry should equal the total input from
that industry since demand is zero. Two conditions:
 cij ≥ 0
 Σcij = 1, j = 1, . . . , n
 Market demand is ignored. Therefore,
p = Cp Cp – p = 0 (C – I)p = 0
 Since each column of C’s entries has a sum of one, the row
vectors of (C – I) add to zero. Therefore, (C – I) is singular. Thus, one
is an eigenvalue of C, and p has a nontrivial solution.
 Note that p, in the closed model, can have multiple correct values
since it is an eigenvector.
n
i = 1
(Leon)

23. Closed Model Example
 Assume we have a consumption matrix such that
C =
 We want to find a solution for p such that (C – I)p = 0 where p
is an eigenvector of C and λ= 1 is an eigenvalue of C.

24. Closed Model Example (cont.)
 C – λI =
 But we know λ= 1, so C – 1I =
 It follows that the eigenspace is span(13, 2, 16)T.
 Therefore, p equals any multiple of the vector (13, 2, 16)T.

25. Works Cited
“Application to Economics: Leontief Model.” Web.
<www.math.ksu.edu>.
Daddel, Alli. Leontief Input Output Model. 19 Sept. 2000. Web.
<www.math.ucdavis.edu>.
Leon, Steven. Linear Algebra with Applications. 8th ed. Upper
Saddle River, NJ: Pearson Education Inc., 2010. Print.
Leontief Input-Output Model in Economics. Web.
<mavdisk.mnsu.edu>.
Leontief Input Output Model: Lecture 32. Web. <barnyard.syr.edu>.
Rincon, Maria. The Leontief Input-Output Model. 2009. Web.
<web.csulb.edu>.
“Sector.” Investopedia. Web. <www.investopedia.com>.
“Wassily Leontief.” Library of Economics and Liberty. 2008. Web.
<www.econlib.org>.