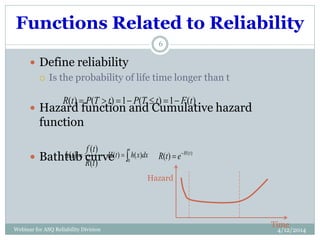
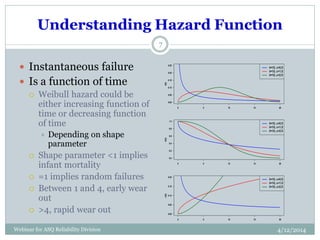
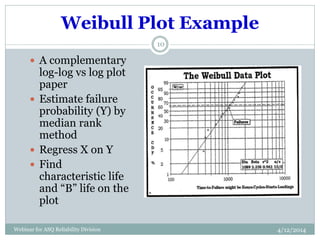
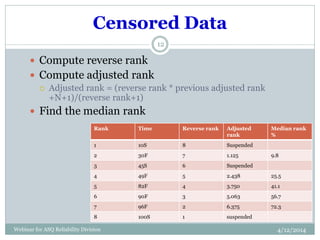
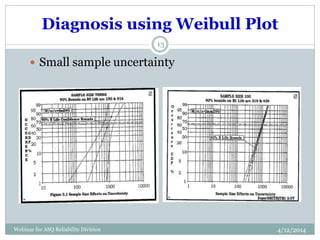
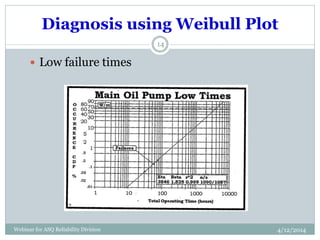
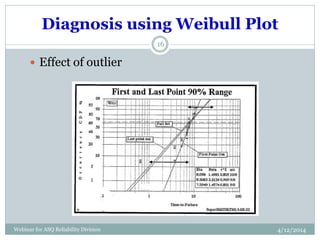
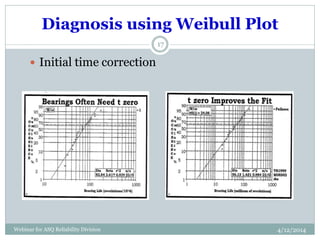
The document introduces Weibull analysis, focusing on understanding the Weibull distribution, utilizing Weibull plots for failure time analysis, and applying software for data analysis. It details the history of Weibull distribution, its parameters, and connections to other statistical distributions, along with methodologies for parameter estimation and diagnosis of failure modes. The document emphasizes the importance of Weibull regression in reliability engineering, recommending the use of software tools for advanced analysis.