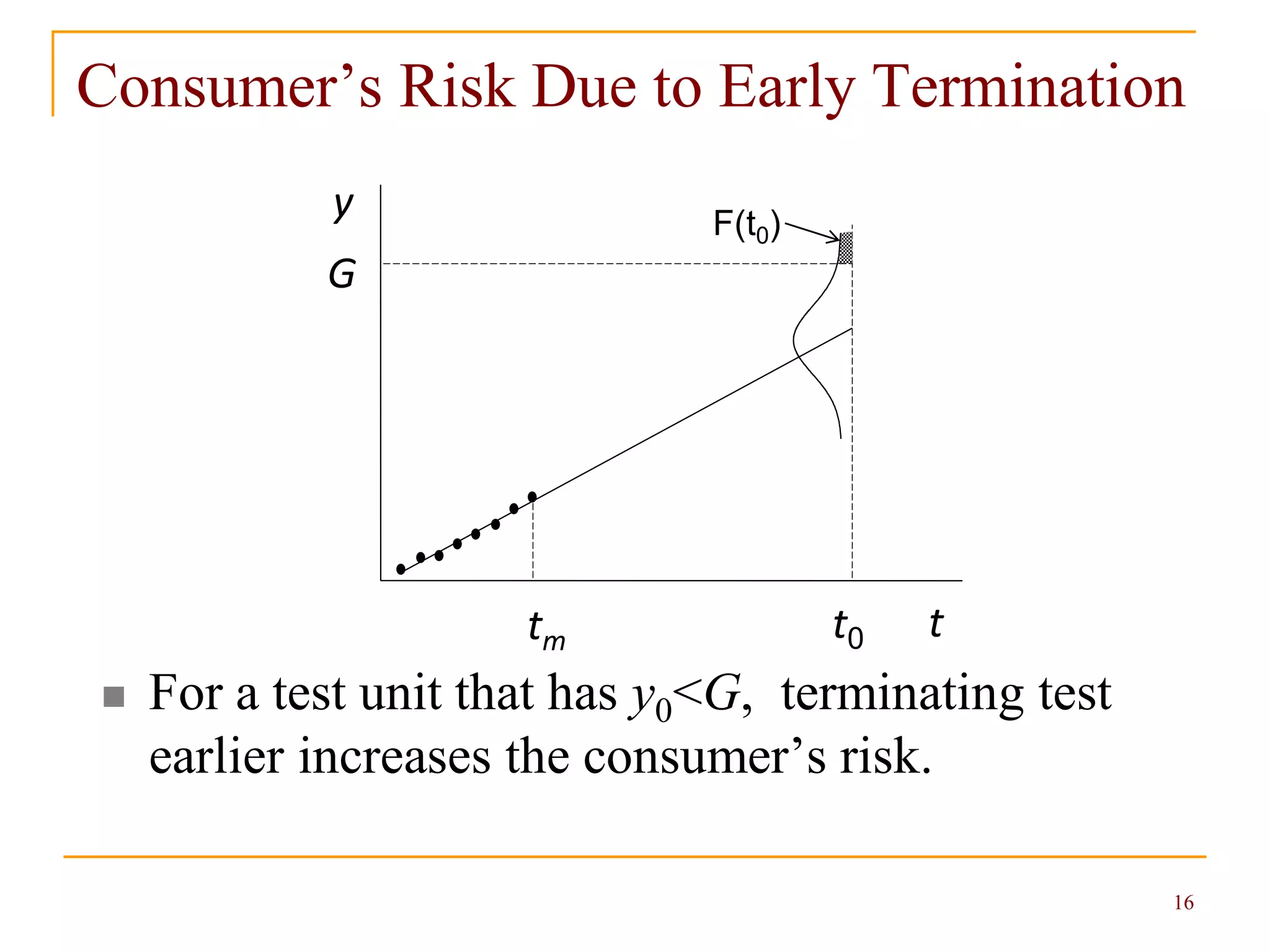
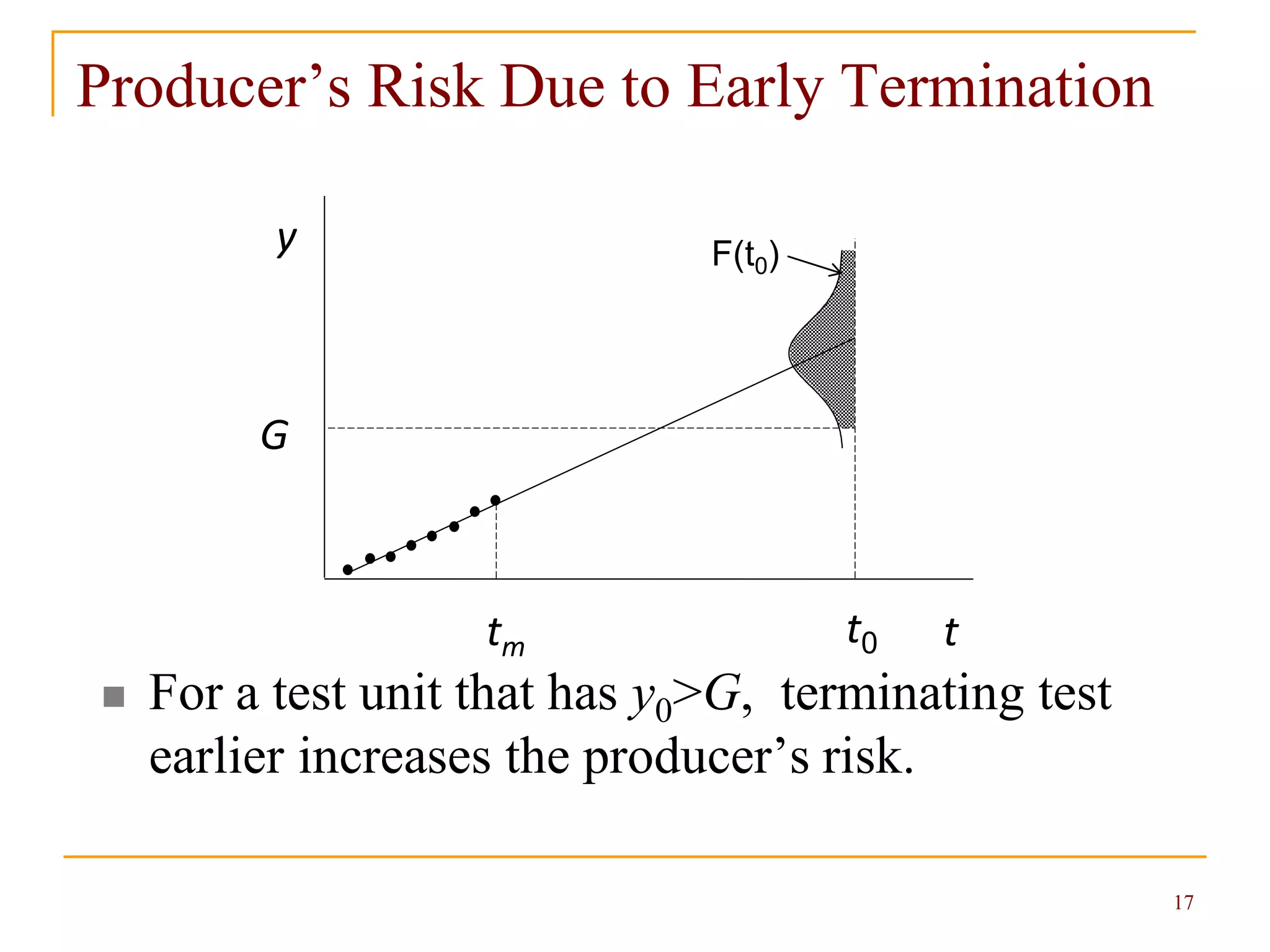
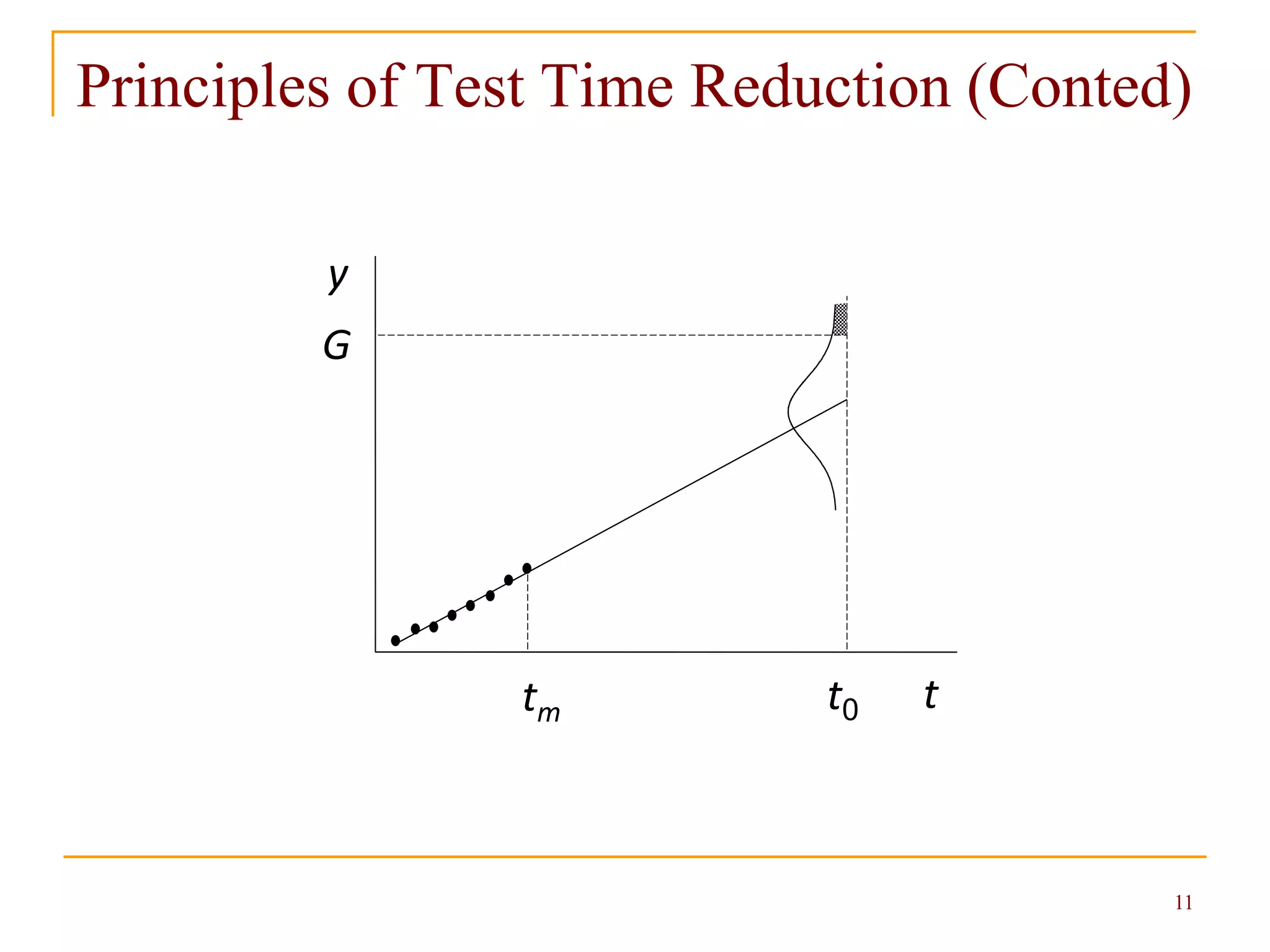
This document discusses efficient reliability demonstration tests that can reduce sample sizes and test times compared to conventional methods. It presents principles for test time reduction using degradation measurements during testing. Methods are provided for calculating optimal test plans that minimize costs while meeting reliability requirements and risk constraints. Decision rules are given for terminating tests early based on degradation measurements and risk estimates. An example application demonstrates how the approach can significantly reduce testing costs.

1. Efficient Reliability
Demonstration Tests
快速可靠性验证试验
Guangbin Yang

2. ASQ Reliability Division
Chinese Webinar Series
One of the monthly webinars
on topics of interest to
reliability engineers
To view upcoming or recorded webinars visit us today at
www.asqrd.org

3. Efficient Reliability Demonstration Tests
快速可靠性验证试验
Guangbin Yang (杨广斌), Ph.D.
Ford Motor Company, Dearborn, Michigan, U.S.A.
Email: gbyang@ieee.org

4. 4
Overview
1. Introduction
2. Sample sizes for bogey tests (zero-failure tests)
3. Principles of test time reduction
4. Test cost modeling
5. Risk of early termination of the test
6. Optimal test plans
7. Procedures of test time reduction
8. Application example
9. Summary and conclusions

5. 5
Bogey Testing (Zero-Failure Test)
 Bogey test is widely used in industry to
demonstrate, at a high confidence, that a product
achieves a specified reliability.
 This test method requires a sample of
predetermined size to be tested for a specified
length of time.
 The required reliability is demonstrated if no
failures occur in the testing.
 So a bogey test is sometimes called the zero-
failure test.

6. 6
Motivation
 A bogey test requires a large sample size and
excessive test time.
 For example, to demonstrate that a product has
95% reliability at 1 million cycles with 95%
confidence, a bogey test requires 59 samples, each
tested for 1 million cycles.
 In the current competitive business environment,
the sample size and test time must be reduced.

7. 7
Sample Size for Conventional Binomial
Bogey Testing
 In some applications, life distribution is unknown.
 To demonstrate at a 100(1–)% confidence that a
product achieves the reliability R0 at time t0, a
sample of size n1 is drawn from a population,
where
 Each of the n1 units is tested for t0. If zero failures
occur during testing, the reliability is demonstrated.
)ln(
)ln(
0
1
R
n



8. 8
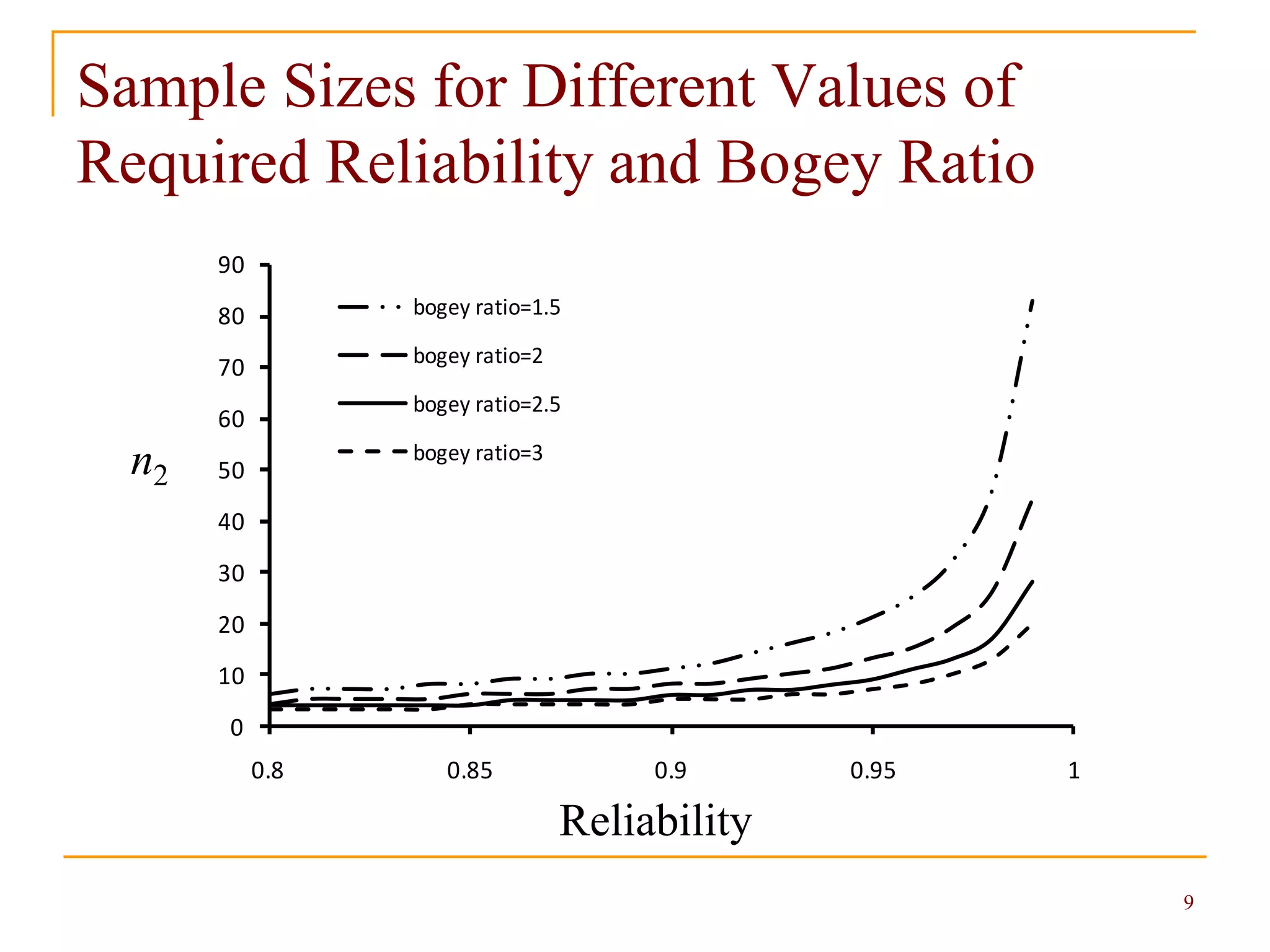
Sample Size for Conventional Lognormal
Bogey Testing
 In some situations, the life of products can be
reasonably modeled by lognormal distribution.
 The minimum sample size to demonstrate the
reliability requirement is
where  is called the bogey ratio, which is the ratio
of actual test time to t0.
 The equation indicates that the sample size can be
reduced by increasing the test time.
)]}1(/)ln([ln{
)ln(
0
12
R
n

 



9. 9
Sample Sizes for Different Values of
Required Reliability and Bogey Ratio
0
10
20
30
40
50
60
70
80
90
0.8 0.85 0.9 0.95 1
bogey ratio=1.5
bogey ratio=2
bogey ratio=2.5
bogey ratio=3
Reliability
n2

10. 10
Principles of Test Time Reduction
 For some products, a failure is said to have
occurred when a performance characteristic
exceeds its threshold.
 For these products, it is possible to measure the
performance characteristic during testing.
 The degradation measurements can be used to
reduce the test time.

11. 11
Principles of Test Time Reduction (Conted)
y
G
t0tm t

12. 12
Principles of Test Time Reduction (Conted)
y
G
ttm t0

13. 13
Principles of Test Time Reduction (Conted)
y
G
t0tm t

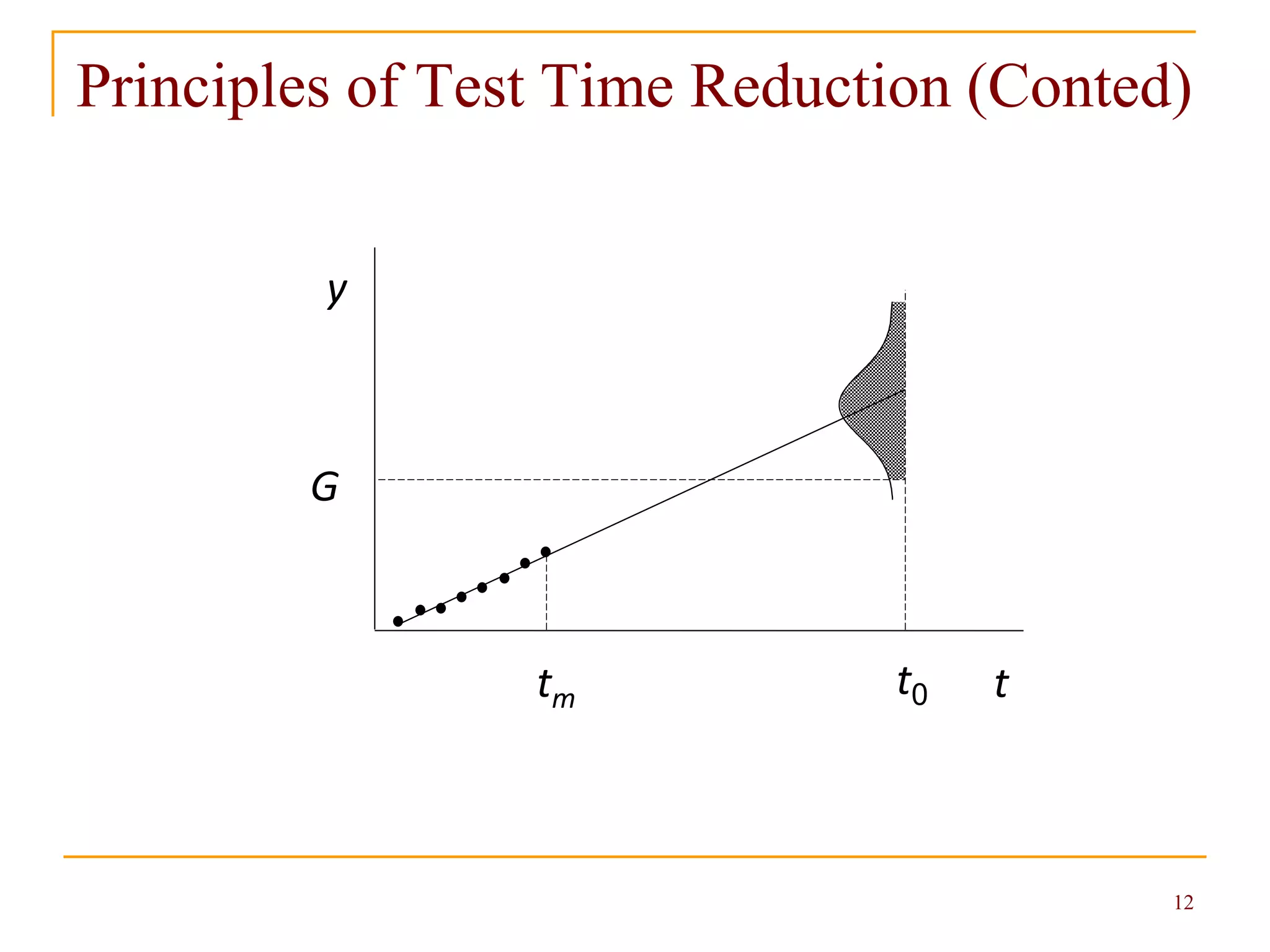
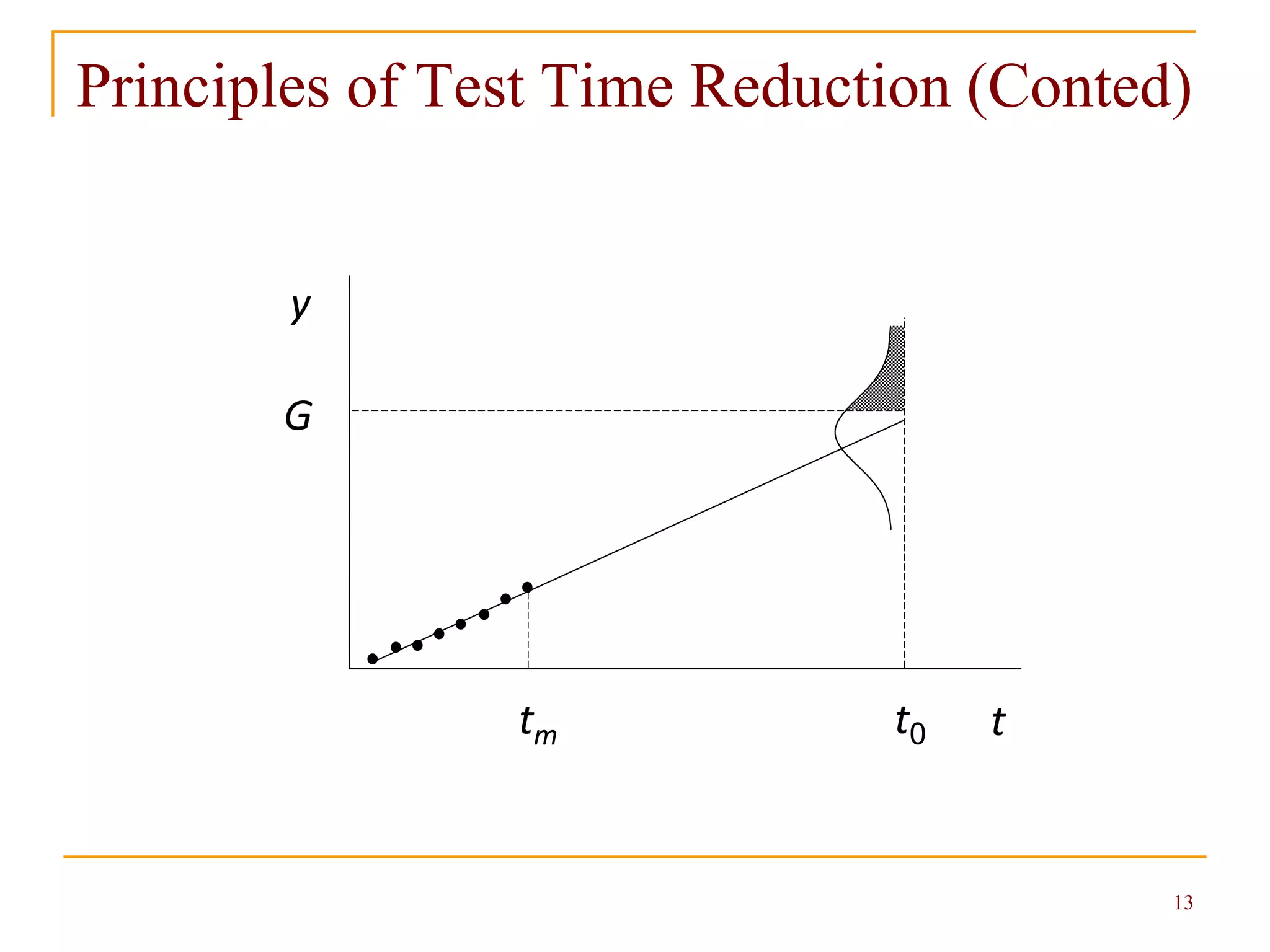
14. 14
Sample Size for Reduced Test Time
 When the test time is reduced, the type II error is
increased by c.
 The minimum sample size for the lognormal
distribution is
where  = c /.
)]}1(/)ln([ln{
)1ln()ln(
0
13
R
n


 



15. 15
Test Cost Modeling
 The cost of a bogey test consists of
 the cost of conducting the test,
 the cost of samples, and
 the cost of measurements.
 Cost model
)(
)]}1(/)ln([ln{
)1ln()ln(
),( 32
0
101 mcc
R
tcTC 


 




16. 16
Consumer’s Risk Due to Early Termination
 For a test unit that has y0<G, terminating test
earlier increases the consumer’s risk.
y
G
t0tm t
F(t0)

17. 17
Producer’s Risk Due to Early Termination
 For a test unit that has y0>G, terminating test
earlier increases the producer’s risk.
y
G
ttm t0
F(t0)

18. 18
Risk Formulation
 For a linear or transformed linear degradation
model, the risk can be formulated as
where T has the student-t distribution with m-2
degrees of freedom.





















)1(
)2(31
1ˆ
ˆ
Pr)(
22
2
0
0
mm
mm
m
yG
TtF




19. 19
Optimal Test Plans
 The test plans are characterized by  and .
 The values of  and  are optimized by
minimizing the total cost TC(, ), while the
following constraints are satisfied:
(1) The risk associated with early termination of a test
must not exceed c/n3.
(2) The sample size must not be greater than the number
of available test units.
 The optimization model can be calculated using
Excel Solver.

20. 20
Procedures of Test Time Reduction
 During testing, each unit is inspected periodically
to measure y. When there are three measurements,
a degradation model is fitted to the data, and the
estimates of the model parameters and the risk
F(t0) are calculated.
 Then we make one of the following decisions
based on the estimates.

21. 21
Test Termination Rules
(1) If , then terminate the test of the unit.
This test unit passes the bogey test.
(2) If , where  is the specified type I error,
then terminate the test of the unit. This test unit fails
to pass the bogey test.
(3) If , continue the test until
decision rule (1) or (2) is met, or until t0 is reached,
whichever occurs sooner.
30 /)(ˆ ntF 
30 /1)(ˆ ntF 
303 /1)(ˆ/ ntFn  

22. 22
Application Example
 Problem statement
A part is required to have a reliability of 95% at a
design life of 1.5105 cycles under the 95th
percentile of the customer usage profile. The part
fails due to its stiffness degradation; a failure is
said to have occurred when the stiffness degrades
to 20% of the initial value. We want to demonstrate
the reliability at a 95% confidence level.

23. 23
Test Plans
 The calculation of optimization model for the test
plan gives  = 0.3147, and  = 0.631.
 Then the test plan is to test 39 samples and the
expected test time is 1.325105 cycles.
 In contrast, the conventional bogey test requires
testing 59 samples for each 1.5105 cycles, or 39
units each for 2.1105 cycles.

24. 24
Decision Rules
 The decision rules for terminating the test of a
part are as follows.
(1) If , then terminate the test of the
unit. This test unit passes the bogey test.
(2) If , then terminate the test of the unit.
This test unit fails to pass the bogey test.
(3) If , continue the test of the
unit until decision rule (1) or (2) is met, or until
2.1105 cycles is reached, whichever occurs first.
3
0 10403.0)(ˆ 
tF
9987.0)(ˆ
0 tF
9987.0)(ˆ10403.0 0
3
 
tF

25. 25
Summary and Conclusions
 The conventional binomial bogey test requires a
large sample size and excessive test time.
 If the life is known to be lognormal, the bogey
test sample size can be reduced by extending the
test time.
 For products subject to degradation failure, the
test time can be reduced substantially by using the
degradation measurements.

26. 26
Additional Readings
 G. Yang, “Reliability Demonstration Through
Degradation Bogey Testing,” IEEE Transactions
on Reliability, vol. 58, no. 4, December 2009.
 G. Yang, “Optimum Degradation Tests for
Comparison of Products,” IEEE Transactions on
Reliability, vol. 61, no. 1, March 2012.
 G. Yang, Life Cycle Reliability Engineering,
Wiley, 2007. (Chapter 9)