Design For Reliability

Design for Reliability
Hilaire Ananda Perera

Define
Measure
Analyze
Improve
Control

ES&S DFSS - Design For Reliability
July 2002

Honeywell Toronto …………. …. 1

USE OR DISCLOSURE OF DATA CONTAINED ON THIS SHEET IS SUBJECT TO THE RESTRICTIONS ON THE TITLE PAGE OF THIS DOCUMENT

Contents
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

What is Reliability
Designing for Reliability
Design for Performance and Reliability Concurrently
Reliability Design Tasks
Derating
Accelerated Life Testing (ALT)
Reliability Estimation
Significance of Weibull β values
Gamma Function Assessment
Prediction Models
Stress/Strength Interference & Probabilistic Design
Reliability Estimation with Safety Margin
Mean and Variance for Any Distribution
Binary Synthesis of Classical Equations
Mean and Standard Deviation of an Algebraic Function
Statistical Data from a Tolerance Statement
False Alarm Probability Estimation

July 2002



Contents
•
•
•
•
•
•

cntd.

Screening Strength Estimation
Adaptive Environmental Stress Screening
How CDE Model Parameters Obtained
Product Assurance Rolled Throughput Yield (RTY)
The Challenge: DFR Physics of Failure Approach
Types of Failure Mechanisms

July 2002



What is Reliability ?

• Reliability is the likelihood(probability) that a
product will
– perform its intended function
– within specified tolerances
– under stated conditions
– for a given period of time

July 2002



Designing for Reliability

• Reliability part of the core design team
• Reliability modeling guides design

• Failure mechanisms designed-out
• Super-accelerated life testing saves time
• Lifetime is metric for design suitability
• Longer lived products
• Reduce manufacturing variability

Iterative Approach
to Reliability
• Test and fix methodology

• Modeling for performance
• Single stress environmental testing
• 1000 hrs or longer per test
• Designing to specifications

July 2002

Gap-Bridging Steps

Cycle Time Reduction

Designing for
Reliability

• Understand Failure Mechanisms

• Share Internal Knowledge
• Develop Reliability Databases
• Deploy Super-accelerated Life Testing



Design for Performance and Reliability Concurrently

Time & Money Saved

Reliability

Target
Enhanced
Design

Redesign
Design

Time & $

Spending More Time in Design Speeds Time to Market

July 2002



Reliability Design Tasks

Reliability Design Tasks should be performed as early as possible in the
product development and iterated as necessary to effectively impact the
product design, emphasizing the need for up-front reliability design
Program Phase and Scope of Reliability Tasks
Program Phase
Concept and Planning

•
•
•

Design and
Development

•

•
•

Production and
Manufacturing

•

Purpose
Study product feasibility
Consider alternate solutions
Understand design & operating
environmemt
Define approaches & solutions
for producing a product
Develop models or prototypes
Validate through test, analysis or
simulation
Maintain inherent product
reliability

•
•
•
•
•

•

•

•

•

July 2002

Scope of Task
Trade-off analysis for critical items
Customer needs refined
Part selection alternatives evaluated
Environmental aspects determined
Integration of design & application
guides
Evaluation of design progress
through analyses and/or tests
Construction of product evaluation
processes
Implement process control and
quality assurance procedures
Operating & maintenance manuals
refined



Derating

Purpose: The purpose of Derating is to enhance the item inherent design
reliability, increase safety margins and reduce repair and replacement
costs. The enhancement is accomplished by compensating for many variables
inherent in any design, some of which include:

What % of the
Maximum
Allowed ?

• Manufacturing Tolerances
• Component Variation
• Material Differences
• Performance Anomalies
• Parameter Drift

Benefits: From an electronic component application, the benefits include lower
failure rates through reduced stresses, less impact from material and
manufacturing variability, proper circuit operation with part parameter changes and
reduction in end of life failures. For mechanical and structural components, a
reduction in stress or increase in strength means a greater factor of safety from
catastrophic failure

July 2002



Accelerated Life Testing (ALT)

Accelerated Life Testing involves measuring the performance of the
product at accelerated load or stress conditions, in order to induce
pattern failures quickly. The goal is to accelerate failure mechanisms
and the accumulation damage, reducing the time-to-failure. Proper
ALT requires that:

• The failure mechanisms in the accelerated environment are the same as
those observed under normal operating conditions;

• Acceleration transforms are available to confidently extrapolate from the
test life to the usage life of the product under actual operating conditions;

• The failure probability density functions at normal operating levels and
under accelerated conditions are consistent

July 2002



Reliability Estimation

Reliability R(T) of a Device with a Mean Time (Hours) To Failure of “MTTF” for a specified
Mission Time of “T” Hours using the Weibull reliability function is:

β


R (T ) = e

 T
 1
−
⋅Γ  1+  
 MTTF  β  

If β = 1; MTTF = 30000 Hrs and T = 2 Hrs
Reliability = 0.99993. This means
99.99% of the missions will be
completed successfully
within 2 Hrs

β is the Weibull Shape Parameter. For an Electronic Device, β = 1 (Exponential Distribution) in
the Useful Life period. Γ represents the Gamma Function. Actual β values to determine
Reliability can be derived using Time To Failure data of End-Units from the operating field

July 2002



Significance of Weibull β Values
Value of β
β<1

β=1

Product Characteristics
Implies infant mortality. If
product survives infant
mortality, its resistance to
failure improves with age
Implies failures are random in
occurrence. An old part is just
as good (or bad) as a new part
Implies early wearout

If This Occurs, Suspect the Following
•
•
•
•
•
•
•
•
•

β>1&<4

•
•

β>4

Implies old age (rapid) wearout

•
•
•

July 2002

Inadequate environmental stress screening
Quality problems in components
Quality problems in manufacturing
Rework/refurbishment problems
Maintenance/human errors
Failures are inherent, not induced
Mixture of failure modes
Electromigration
Low cycle fatigue
Corrosion or erosion failure modes
Scheduled replacement may be cost
effective
Inherent material property limitations
Gross manufacturing process problems
Small variability in manufacturing or
material



Gamma Function Assessment

Enter the “z”
Value Here

This is the
Calculated
Gamma Value

July 2002



Prediction Models
– IEEE 1413 Reliability Prediction Process Guide
 Framework for Hardware & Software predictions at all levels

– Telcordia TR-332 (previously known as Bellcore)
– RDF 2000 (French)
– MIL-HDBK-217F, N2
 Piece-part reliability prediction, sum defect rates
 No new technology or high complexity models - obsolete
 Need to find a replacement . . . . .

– RAC PRISM
 Forces holistic consideration of factors influencing Reliability
– Mission & Duty cycle
– All processes
– Devices

July 2002



Stress/Strength Interference & Probabilistic Design

Reliability prediction using the Stress/Strength Interference and
Probabilistic Design method:
This method assumes that the material properties are time independent
because of their slow change, and the components are not subjected to wear
related failure modes. When components are subjected to reversing mechanical loads that
exhibit a single failure mode, the reliability is designed-in by selecting the probability number
representing the Safety Margin. For the use of this methodology, Binary Synthesis of the
classical equations are needed.

Safety Margin (SM) =

Reliability (R) = 1 -

July 2002

µS − µs
σ S 2 + σ s2

1
2Π

∫

SM

−t 2
2

µs = Mean Stress of the Stress function
σs = Standard Deviation of the Stress
µS = Mean Strength of material
σS = Standard Deviation of the material Strength
If SM = 3.5
Reliability = 0.9997

e dt

−∞



Reliability Estimation with Safety Margin

To obtain Reliability,
Go Here and Select
Standard Normal
Cumulative Distribution
Enter “SM” Value
to “Z”

Reliability = 0.999767

July 2002



Mean and Variance for any Distribution

Let f(x) = Probability Density Function of the independent variable x
If f(x) ≥ 0, for all x
+∞

∫

Mean = µ = xf ( x )dx
−∞

Coefficient of Variation (CV)
provides a relative measure of data
dispersion compared to the Mean
CV =

+∞

σ
µ

∫

2
2
Variance = σ = ( x − µ ) f ( x )dx , where σ = Standard Deviation
−∞

When “x = Time”, Lower boundary of the Integral will be 0 instead of -∞
This is the case for Reliability related functions

July 2002



Binary Synthesis of Classical Equations
In a pressurized cylinder wall of “External Radius = a” and “Bore Radius = b”, the Failure Governing
Stress Function (s) is the Circumferential (Hoop) Stress

s =

  a 2 
   + 1
b
P.   2 

a
   − 1

b

Where P = Internal Pressure

For Reliability calculation using Safety Margin determine the Mean (µ) and the
Standard Deviation (σ) of the variables “a”; “b”; “P” and calculate the µ & σ of
the Stress Function (s)
Note: The methodology for µ and σ calculation is in the slides named Mean and Standard Deviation of an Algebraic
Function and Statistical Data from a Tolerance Statement

July 2002



Mean and Standard Deviation of an Algebraic Function
Algebraic
Function
c
c.x
c.x + d
c.x - d
x+y
x–y
* x.y

Mean

Standard Deviation

c
c.µx
c.µx + d
c.µx - d
µx + µy

0
c.σx
c.σx
c.σx

µx - µy

(µ

µx . µy

x
*
y

µx
µy

n

µxn

* x
* x

0.5

(σ
(σ

(0.5. 4.µ

2
x

− 2.σ x

2
x

)

0.5

+σ y

2 0.5

2

+σ y

2 0.5

x
x

.σ y + µ y .σ x + σ x .σ y
2


 1
µ
 y

2

)
)

2

(µ

2

2

  µ x .σ y + µ y .σ x
.

µ y2 +σ y2

( n −1)
n.µ x
.σ x
2

2

2

− 0.5. 4.µ x − 2.σ x
2

x

2

2






2

)

2 0.5
0.5

)

0.5

c, d, n are constants
* These are good approximations when the Coefficient of Variation (CV) is small. i.e. CV < 0.1

July 2002



Statistical Data from a Tolerance Statement
When the distributional Probability Density Function of a variable is Normal
(or Gaussian) between the limits Low “a” and High “b”

The Mean (µ) is approximately equal to

a+b
2

The Standard Deviation (σ) is approximately equal to

For a 10K Ohms Resistor with
±5% tolerance
µ = 10K Ohms
σ = 167 Ohms

b−a
6

These simplified calculations are based on theoretical derivations and was justified by
E. B. Haugen in University of Arizona, 1974

July 2002



False Alarm Probability Estimation

Voltage Divider Circuitry for Min_Limit & Max_Limit
Tested Output Voltage = 12V +/- 180mV µ = 12 ; σ = 0.06

Resistor
X

VRef = 15V +/- 180 mV

Resistor
Y

VTest = (Y/(X+Y))* VRef.

µ = 15; σ = 0.06

Grnd

False Alarms can happen
due to Component
Tolerances and Voltage
Deviations

Resistor Tolerance is +/- 10%

Case 1: Min_Limit; X=100K Ohms; Y=302K Ohms µ (VTest) = 11.27 ; σ(VTest) = 0.064
Safety Margin (SM) = 8.343

Probability of Failure = 0.00E+00

Case 2: Max_Limit; X=100K Ohms; Y=541K Ohms µ (VTest) = 12.66 ; σ(VTest) = 0.079
Safety Margin (SM) = 6.679

Probability of Failure = 1.2084E-11

False Alarm Probability = 1.2084E-11
July 2002



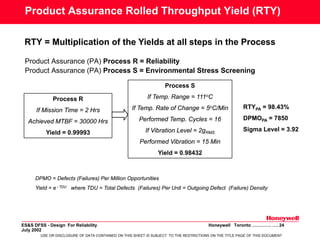
Screening Strength Estimation
The Screening Strength of a given stress screen profile is defined as the
probability that the stress screen will precipitate a latent defect into a
detectable failure, given that a defect is present. Screening provide
assurance on the Outgoing Reliability
Screening Strength for Temperature Cycling (STn) is a function of Temperature Range =T;
Temp. Rate of Change =R; Number of Cycles =n

STn

= 1 − e[−[0.0017⋅(T + 0.6)

0.6

⋅ln(e + R ) ⋅n]]
3

Screening Strength for Random Vibration (SVt) is a function of G = gRMS; Vibration Duration = t

SVt

= 1 − e[−(0.0046⋅G

1.71

⋅t )]

Combined Screen Strength (SS) = 1 - (1-STn).(1-SVt)

When T = 111oC; R = 5oC/Min
n =16 Cyc; G = 2gRMS;
t = 15 Min
SS = 0.98432

The Screening Strength equations were developed by Hughes Aircraft Company, and modified by Rome Air
Development Centre (RADC) based on the data from McDonnel Aircraft Co. and Grumman Aerospace
Corporation

July 2002



Adaptive Environmental Stress Screening (ESS)
The principle of adaptive screening is to adjust the screens on the basis of
observed screening results, so that the screens are always most costeffective while meeting ESS program goals. Contract terms should be
flexible enough to permit modifications of screening parameters when such
modifications can be shown to be beneficial
The Chance Defective Exponential (CDE) Model is the chosen prediction model for failure rate
distribution analysis, as the constant failure rate portion could be extracted for Acceleration
Factor calculation, the average rate of defect precipitation determined for Best Thermal Cycling
Time and Failure Free Time calculation. CDE equation parameters are obtained using the
SigmaPlot computer program
P/N XXXX100-07 ESS
Period: 01 Jan 99 - 31 Dec 99
0.04
Failure
Rate (fr)
0.03
Fail/Hour

Outgoing Defect Density = 5300 PPM
Yield = 0.9947
4σ < Capability < 5σ
Time To Remove 99.999% Defects = 32 Hrs
Failure Free Time (99.99% Yield) at 90% LCL = 20Hrs

0.02

fr = 0.0031+ 0.0385*exp(-0.3669*t)

0.01

0.00
0

2

4

6

8

10

12

14

16

18

20

22

24

26

28

30

32

34

36

38

40

ESS Time (t) Hours

CONDITION: Cumulative Thermal Energy due to previous runs And/Or NFF
And/Or BIE Failure are also responsible for relevant failure precipitation

July 2002



How CDE Model Parameters Obtained

Time To
Failure
Data

Failure
Rate
Data

July 2002

CDE Model
Parameters

Coefficient of
Variation (CV)
used as a gauge
of the accuracy
of the fitted
curve parameters



Product Assurance Rolled Throughput Yield (RTY)
RTY = Multiplication of the Yields at all steps in the Process
Product Assurance (PA) Process R = Reliability
Product Assurance (PA) Process S = Environmental Stress Screening
Process S
Process R

If Temp. Range = 111oC

If Mission Time = 2 Hrs

If Temp. Rate of Change = 5oC/Min

RTYPA = 98.43%

Achieved MTBF = 30000 Hrs

Performed Temp. Cycles = 16

DPMOPA = 7850

Yield = 0.99993

If Vibration Level = 2gRMS

Sigma Level = 3.92

Performed Vibration = 15 Min
Yield = 0.98432

DPMO = Defects (Failures) Per Million Opportunities
Yield = e - TDU where TDU = Total Defects (Failures) Per Unit = Outgoing Defect (Failure) Density

July 2002



The Challenge

DFR Physics of Failure Approach
The Physics of Failure (PoF) approach to Design for Reliability is
founded on the fact that the failure of electronics is governed by
fundamental mechanical, electrical, thermal and chemical
processes.
By understanding the possible failure mechanism, design teams
can identify and solve potential reliability problems before they
arise. The PoF process can be extremely complex, and so
requires the use of an expert system for its completion

July 2002



Types of Failure Mechanisms
Overstress failure
mechanisms occur when a
stress excursion exceeds
strength

Wear-out failure
mechanisms occur when
accumulated damage
exceeds endurance

Mechanical
•
Fracture
•
Buckling
•
Yielding

Mechanical
•
Fatigue
•
Creep
•
Corrosion

Electrical
•
Fused or shorted wires
•
Electrostatic discharge
•
Electrical overstress

Electrical
•
Leakage current
•
Metal migration
•
Threshold voltage shift

Thermal
•
Melting

Thermal
•
Elasticity degradation

Physical/Chemical
•
Electron-hole pairs generation
due to ionizing radiation

Physical/Chemical
•
Interdiffusion
•
Depolymerization

July 2002



Design For Reliability

More Related Content

What's hot

Viewers also liked

Similar to Design For Reliability

More from Hilaire (Ananda) Perera P.Eng.

Recently uploaded

Design For Reliability