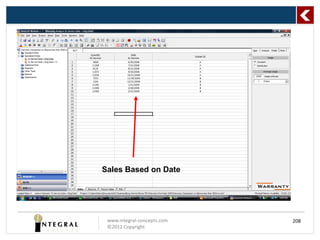
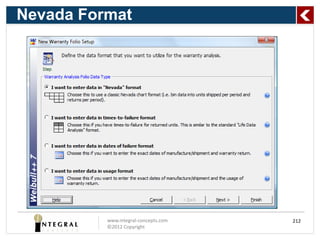
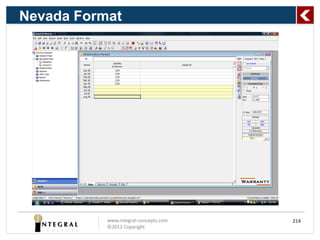
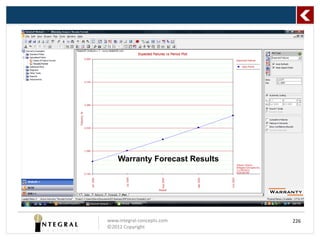
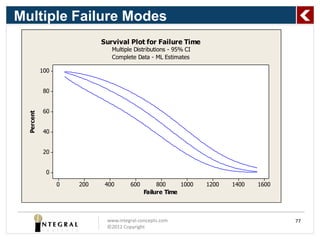
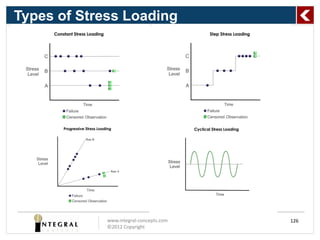
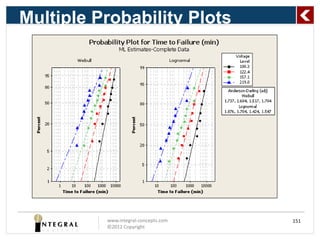
The document presents a comprehensive overview of predicting product life using reliability analysis methods, focusing on various reliability concepts, statistical models, and estimation techniques. It covers topics such as reliability data, types of distributions (like Weibull and exponential), and the significance of censoring in data analysis. The goal is to equip reliability engineers with the knowledge to effectively assess product reliability and improve decision-making in product development.



























![Exponential Distribution
• pdf: f(t) = le-lt
• cdf: F(t) = 1 - e-lt
• Reliability: R(t) = e-lt
• Hazard rate: h(t) = l
• MTTF = 1/l = q
• Quantile: F-1(p) = (1/l)[-ln(1-p)]
www.integral-concepts.com 28
©2012 Copyright](https://image.slidesharecdn.com/predictingproductlifeusingreliabilityanalysismethods09apr2012rev1-120316112325-phpapp01/85/Predicting-product-life-using-reliability-analysis-methods-30-320.jpg)























































































































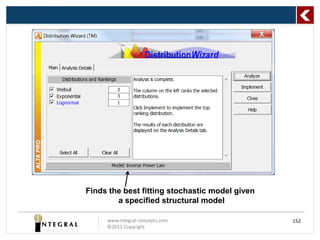



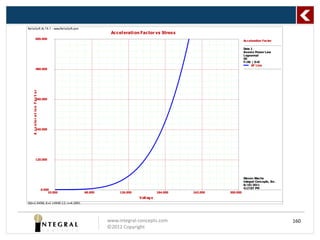
![ReliaSoft AL TA 7 - www.ReliaSoft.com
R el i abi l i ty vs Ti me
1.000
Reliability
CB@90% 2-Sided [R]
Data 1
Inverse Power Law
Lognormal
50
F= | S=
36 0
0.800 Data Points
Reliability Line
Top CB-II
Bottom CB-II
0.600
R e lia b ilit y
0.400
0.200
Steven Wachs
integral Concepts, Inc.
8/19/2011
3:25:11 PM
0.000
0.000 60000.000 120000.000 180000.000 240000.000 300000.000
Time
Std=1.0498; K=1.1494E-12; n=4.2891
www.integral-concepts.com 156
©2012 Copyright](https://image.slidesharecdn.com/predictingproductlifeusingreliabilityanalysismethods09apr2012rev1-120316112325-phpapp01/85/Predicting-product-life-using-reliability-analysis-methods-158-320.jpg)