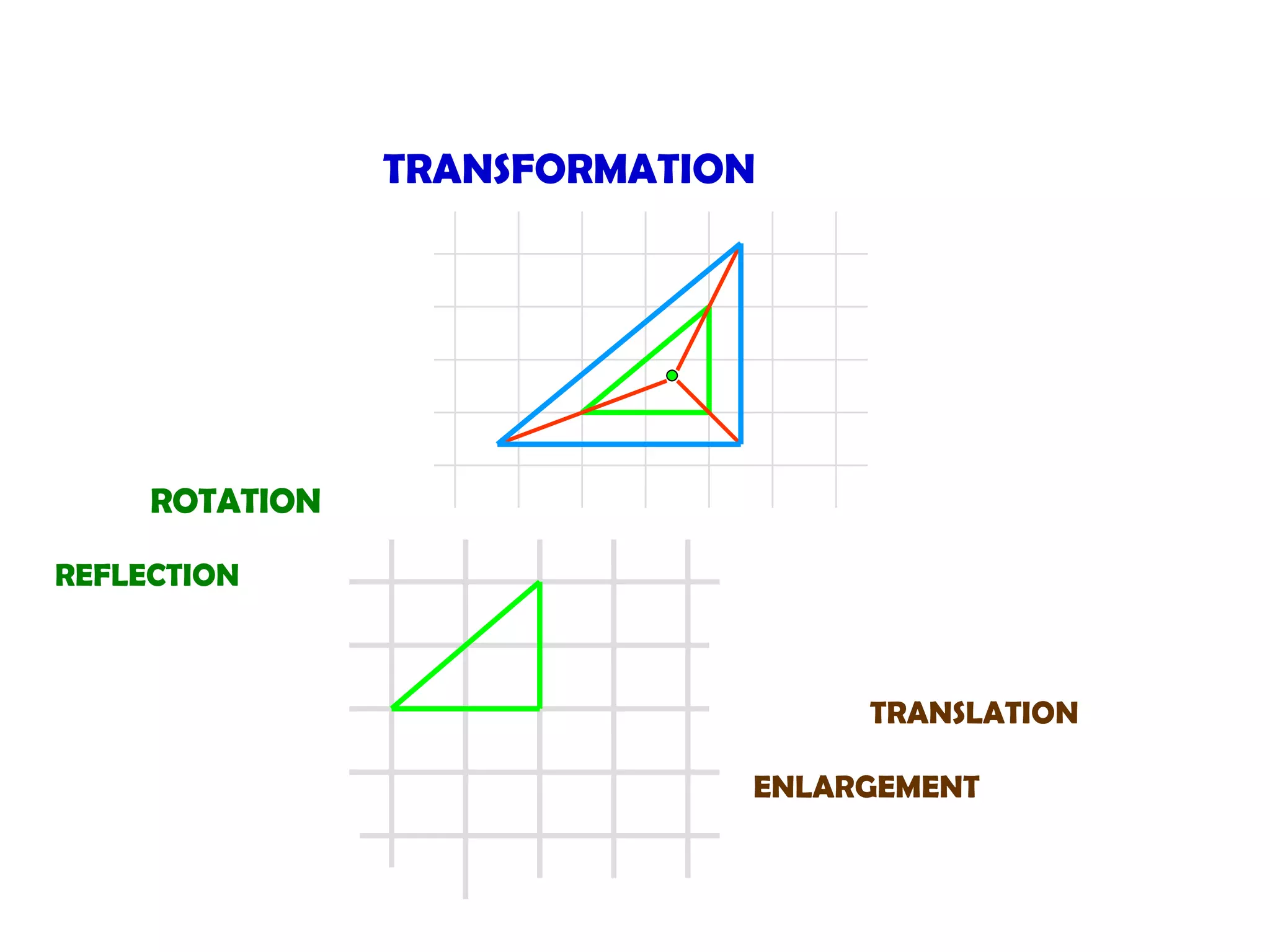
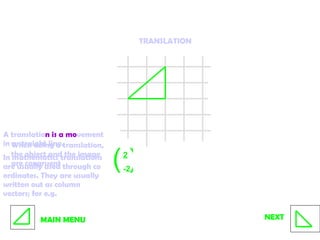
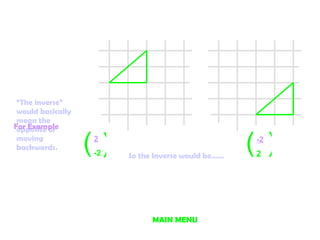
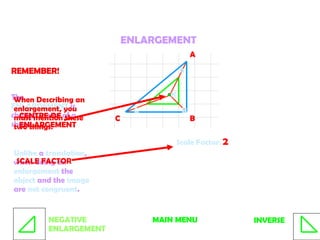
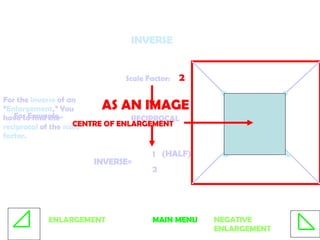
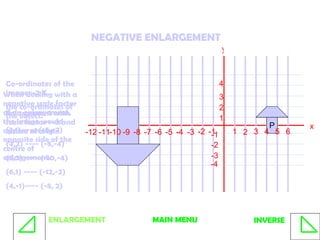
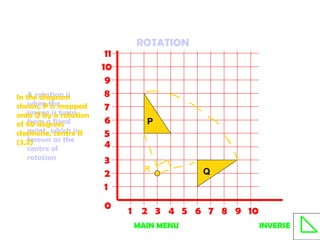
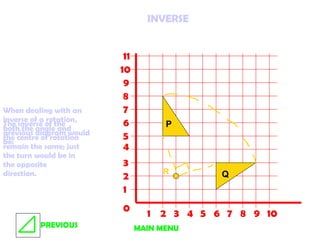
The document discusses different types of geometric transformations including: 1. Translations move objects in a straight line and are written as column vectors. The inverse is the opposite movement. 2. Enlargements change the size of shapes. The image and object are not congruent and the scale factor and center of enlargement must be specified. The inverse has a reciprocal scale factor. 3. Rotations turn objects around a fixed point, the center of rotation. The inverse rotation is in the opposite direction. 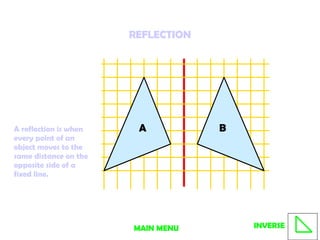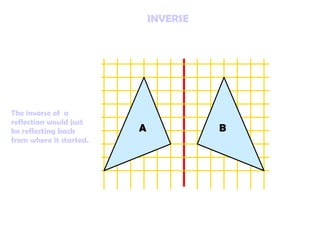4. Reflections move points to the opposite side of a fixed line. The inverse reflects back to the original position. 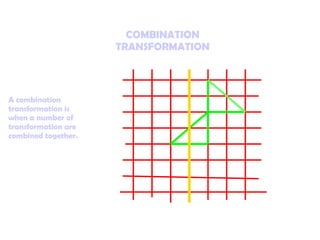5. Combination transformations apply multiple transformations sequentially.

1. TRANSFORMATION TRANSLATION ENLARGEMENT ROTATION REFLECTION

2. TRANSLATION A translatio n is a mo vement in a straight line. In mathematics translations are usually used through co ordinates. They are usually written out as column vectors; for e.g. 2 -2 MAIN MENU NEXT ( ) When doing a translation, the object and the image are congruent

3. + + - - THINGS TO REMEMBER ALWAYS THE FIRST # IN THE COORDINANTS IS FOR GOING HORIZNTALLY AND THE SECOND # IS GOING VERTICALLY! PREVIOUS INVERSE MAIN MENU

4. MAIN MENU “ The inverse” would basically mean the opposite or moving backwards. So the Inverse would be…… 2 -2 ( ) ( ) -2 2 For Example

5. ENLARGEMENT The ENLARGEMENT is change in size of a shape. Unlike a translation , when doing an enlargement the object and the image are not congruent . A B C A B C Scale Factor: 2 K REMEMBER! When Describing an enlargement, you must mention these two things: SCALE FACTOR CENTRE OF ENLARGEMENT MAIN MENU INVERSE NEGATIVE ENLARGEMENT

6. INVERSE For the inverse of an “ Enlargement ,” You have to find the reciprocal of the scale factor. For Example.. Scale Factor: RECIPROCAL 1 (HALF) 2 INVERSE= 2 AS AN IMAGE CENTRE OF ENLARGEMENT MAIN MENU ENLARGEMENT NEGATIVE ENLARGEMENT

7. MAIN MENU INVERSE ENLARGEMENT NEGATIVE ENLARGEMENT When dealing with a negative scale factor of an enlargement, the image would appear on the opposite side of the centre of enlargement. 1 2 3 6 1 2 3 4 x y -1 -2 -3 -4 P 4 5 -1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 Enlargement with scale factor =-2 and centre of origin Co-ordinates of the image=-2 X the co-ordinates of the object. (3,1) ---- (-6,-2) (4,2) ---- (-8,-4) (5,2) ---- (-10,-4) (6,1) ---- (-12,-2) (4,-1)---- (-8, 2)

8. ROTATION A rotation is when the image is turns from a fixed point, which is known as the centre of rotation 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 In the diagram shown, P is mapped onto Q by a rotation of 90 degrees clockwise, centre R (3,2) P Q R MAIN MENU INVERSE

9. 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 P Q R INVERSE When dealing with an inverse of a rotation, both the angle and the centre of rotation remain the same; just the turn would be in the opposite direction. The inverse of the previous diagram would be: MAIN MENU PREVIOUS

10. REFLECTION A reflection is when every point of an object moves to the same distance on the opposite side of a fixed line. A B MAIN MENU INVERSE

11. INVERSE The inverse of a reflection would just be reflecting back from where it started. A B

12. COMBINATION TRANSFORMATION A combination transformation is when a number of transformation are combined together.