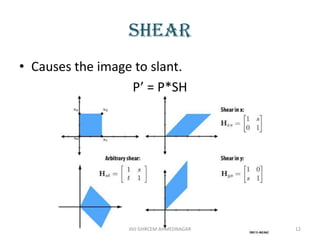
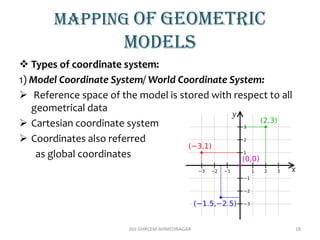
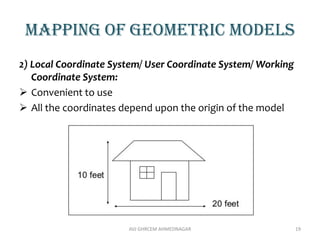
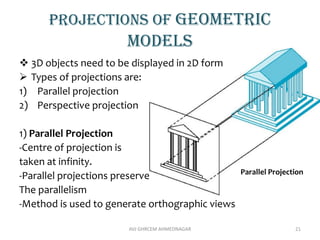
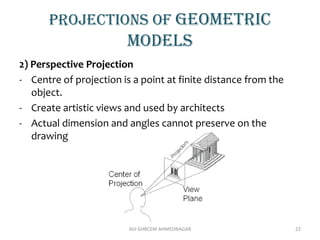
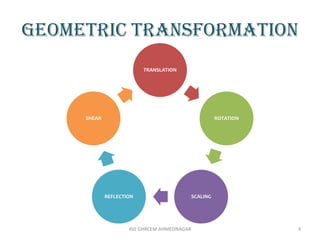
The document provides an introduction to computer graphics, focusing on computer-aided design (CAD) and interactive computer graphics. It covers various geometric transformations such as translation, rotation, scaling, reflection, and shear, including their applications and limitations. Additionally, the text discusses homogeneous coordinates, mapping of geometric models, and the types of projections needed to display 3D objects in 2D form.

1. Chapter 1
computer graphics
S.G.R. Education Foundation
G H RAISONI COLLEGE OF ENGINEERING AND MANAGEMENT
AHMEDNAGAR
NAAC ACCREDITED
(APPROVED BY AICTE, NEW DELHI, RECOGNIZED BY GOVT. OF MAHARASHTRA & AFFILIATED TO SAVITRIBAI PHULE PUNE UNIVERSITY)
- Prof. Aniket V. Joshi
Asst. Professor
Mechanical Engineering Department
GHRCEM, A’Nagar.

2. Introduction
 CAD: use of computer to assist the user in design of system.
Stages in CAD:
Create
Modify
Analyze
Optimize
2
AVJ GHRCEM AHMEDNAGAR

3. Introduction
Interactive Computer
Graphics:
o Displays data and information in
the form of graphics
o Data entered is get converted into
graphical form by using software
and hardware
o User can create, modify and
explore further possibilities and
options
o Major advantage is change in the
image
3
AVJ GHRCEM AHMEDNAGAR

4. GEOMETRIC TRANSFORMATION
TRANSLATION
ROTATION
SCALING
REFLECTION
SHEAR
AVJ GHRCEM AHMEDNAGAR 4

5. GEOMETRIC TRANSFORMATION
 Transformations: changes performed on the original
graphic image by changing database.
 Used to alter the orientation, scale, position of the drawing
 Applications of Transformations:
a. Must be creation of model
b. To express location of objects relative to others
c. To view an object from different positions and directions
d. To perform transformations like translate/move, rotate,
scale, mirror, etc..
e. To obtain orthographic and perspective views of model
f. To create animation
AVJ GHRCEM AHMEDNAGAR 5

6. Formulation
• Point can be represented as P= [x,y]
• Line can be represented as L=
• L’=L [TM] where [TM]= Transformation Matrix
AVJ GHRCEM AHMEDNAGAR 6

7. translation
o Entity of a geometric model remains parallel to its initial
position
o Every point on geometric model moves by equal distance
T = [tx ty]
AVJ GHRCEM AHMEDNAGAR 7
A’B’C’D’ = ABCD + T

8. translation
 Translation can be applied to curves such as circles,
parabolas, surfaces and solids. These shapes are treated as
a geometric entity.
 Limitations for translation of circle:
a) Circle would be broken down into finite points and
transformations for each of these points would then have
to be done
b) Resulting entity would lose its identity of being a circle.
AVJ GHRCEM AHMEDNAGAR 8

9. rotation
 Turning the object through angle ‘θ’ about the origin (@ z
axis).
 Used to view object from different angles.
 Allows the user to create an array of objects.
AVJ GHRCEM AHMEDNAGAR 9
A’B’ = AB * R

10. scaling
 Alters the size of an object.
 It can be Uniform (equal in both X and Y directions) or non-
uniform (different in X and Y directions)
P’ = P * S
[x’ y’] = [x y]
AVJ GHRCEM AHMEDNAGAR 10

11. Reflection (mirror)
 Process of obtaining a mirror of the original shape
 Used in symmetrical objects
P’= P*M
AVJ GHRCEM AHMEDNAGAR 11

12. shear
• Causes the image to slant.
P’ = P*SH
AVJ GHRCEM AHMEDNAGAR 12

13. Homogeneous co-ordinates
 Need:
o For quick and efficient calculations, it is desirable to express
all transformations in the form of multiplications.
o To represent points at infinity and non intersection of
parallel lines.
o To represent multiple operations which include translation.
o To draw perspective views of geometrical models
AVJ GHRCEM AHMEDNAGAR 13

14. Homogeneous co-ordinates
• In homogeneous coordinate system, point P(x, y) can be
expressed as P(x’ y’ h)
Where
AVJ GHRCEM AHMEDNAGAR 14
 h is non zero number, convenient value is 1
General 3x3 matrix for
homogeneous
transformation.
a d 0
b e 0
c f 1

15. Translation
matrix in
homogeneous
form
AVJ GHRCEM AHMEDNAGAR 15

16. Inverse transformations
• Inverse of matrix is another matrix such that when two are
multiplied, an identity matrix results. i.e. T*T-1 = I
• For point p, p’ is transformed point
Then P’= P*T
P’*T-1 = P*T* T-1
P’*T-1 = P*I
P’*T-1 = P
AVJ GHRCEM AHMEDNAGAR 16

17. Concatenated or composite
transformation
AVJ GHRCEM AHMEDNAGAR 17

18. MAPPING OF GEOMETRIC
MODELS
 Types of coordinate system:
1) Model Coordinate System/ World Coordinate System:
 Reference space of the model is stored with respect to all
geometrical data
 Cartesian coordinate system
 Coordinates also referred
as global coordinates
AVJ GHRCEM AHMEDNAGAR 18

19. MAPPING OF GEOMETRIC MODELS
2) Local Coordinate System/ User Coordinate System/ Working
Coordinate System:
 Convenient to use
 All the coordinates depend upon the origin of the model
AVJ GHRCEM AHMEDNAGAR 19

20. Three dimensional
transformations
 The transformation takes place on a 3D plane
 Generalize from 2D by including z coordinate
 Straight forward for translation and scale, rotation
 more difficult
 Homogeneous coordinates: 4 components
 Transformation matrices: 4×4 elements
a b c tx
d e f ty
g h I tz
0 0 0 1
AVJ GHRCEM AHMEDNAGAR 20

21. Projections of geometric
models
 3D objects need to be displayed in 2D form
 Types of projections are:
1) Parallel projection
2) Perspective projection
1) Parallel Projection
-Centre of projection is
taken at infinity.
-Parallel projections preserve
The parallelism
-Method is used to generate orthographic views
AVJ GHRCEM AHMEDNAGAR 21
Parallel Projection

22. Projections of geometric
models
2) Perspective Projection
- Centre of projection is a point at finite distance from the
object.
- Create artistic views and used by architects
- Actual dimension and angles cannot preserve on the
drawing
AVJ GHRCEM AHMEDNAGAR 22

23. 23
AVJ GHRCEM AHMEDNAGAR