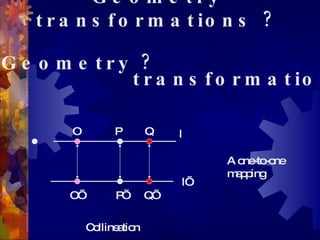
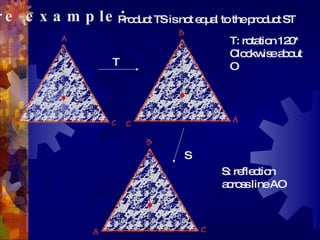
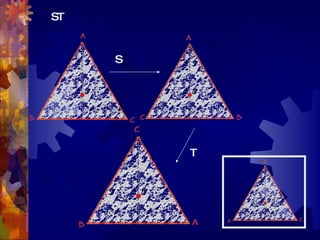
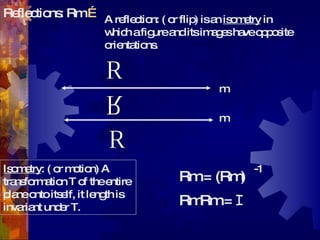
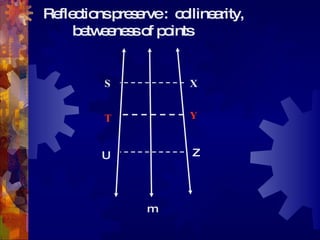
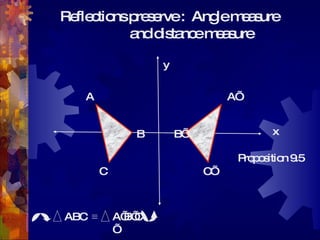
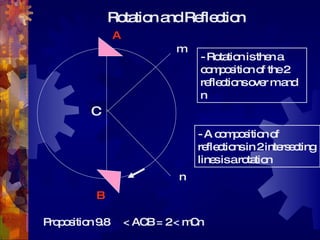
This document discusses geometry transformations, specifically reflections and products of reflections. It defines reflections as isometries that flip a figure across a line of reflection, preserving collinearity, angle measures, and distance measures. Reflections have the property that a reflection followed by itself is the identity transformation. The document explains that translations, rotations, and glide reflections can all be expressed as products of two reflections. Translations are the composition of reflections across parallel lines, rotations are the composition of reflections across intersecting lines, and glide reflections combine a translation with a reflection across a parallel line.

1. Geometry transformations Reflections and products of reflection By: SR. TA

2. Geometry transformations ? Geometry ? A one-to-one mapping transformations ? l l’ O P Q O’ P’ Q’ Collineation

3. More example : Product TS is not equal to the product ST T: rotation 120* Clockwise about O T S S: reflection across line AO

4. ST S T

5. Commute : if 2 transformations S,T happen to have the property ST=TS Commutative : a collection of transformations in which every pair commute

6. Reflections: Rm The fundamental type of motion. m Q A A^m AQ = QA^m m : line of reflection for a A^m : it own image. A : is the reflection of A^m with respect to Q Q: point of reflection

7. Reflections: Rm … R R R m m Rm = (Rm) -1 RmRm = I A reflection: ( or flip) is an isometry in which a figure and its images have opposite orientations. Isometry : ( or motion) A transformation T of the entire plane onto itself, it length is invariant under T.

8. Reflections preserve : collinearity, betweeness of points m S X T Y U Z

9. Reflections preserve : Angle measure and distance measure y x A B’ B C C’ A’ ABC ≡ A’B’C’ ≡ Proposition 9.5

10. Isometries As Products of Reflections The four Euclidean isometries: Reflection Translation Rotation Glide reflection

11. Translation and Reflection X units Translate 2X units to the right m n Translation is equivalent to the composition of 2 reflections, one across m and the other across n - A composition of reflection in 2 parallel lines is a translation Proposition 9.12. Given a line t, the set of translation along t is a commutative group

12. Proposition 9.7 A motion T = I is a rotation if and only if T has exactly one fixed point

13. Rotation and Reflection m n C A B < ACB = 2 < mCn - Rotation is then a composition of the 2 reflections over m and n - A composition of reflections in 2 intersecting lines is a rotation Proposition 9.8

14. Proposition 9.9: Given a point A, the set of rotations about A is a commutative group.

15. Glide and Reflection A glide reflection: is the composition of translation and a reflection in a line parallel to glide vector X units Translate 2X units to the right m n