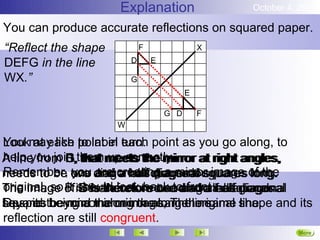
1. The document discusses different types of geometric transformations including reflections, rotations, and translations. 2. A reflection produces a mirror image of an object across a line or plane. Corresponding points on the object and its reflection are equidistant from the line/plane of reflection. 3. A rotation turns an object around a fixed point by a specified angle and direction. To perform a rotation, one traces the object onto tracing paper and rotates the paper around the given point by the required angle and direction.

1. October 4, 2012
Transformation
s
1. Reflections, rotations and translations.
Next

2. Explanation October 4, 2012
Here is a large mirror.
If we place an object in front of it, we see a mirror image.
Notice that any point on the real object real image
Now imagine we could look at both the is the sameand
distance from the overhead.
the reflection fromplane of the mirror in its reflection.
More
Next

3. Explanation October 4, 2012
Each point on the real object has a corresponding point
the same distance from the mirror.
Reflection
Mirror
Real object
A line joining corresponding points will always pass
through the mirror at right-angles to it.
More
Next

4. Explanation October 4, 2012
You can produce accurate reflections on squared paper.
“Reflect the shape F X
DEFG in the line D E
WX.” G
E
G D F
W
Lookmay like point in turn. point as you go along, to
You at each to label each
A line from D,themmeets the mirror at right angles,
help you join that meets the mirror at right angles,
E, that up correctly.
G,
F,
Remember, one and creating a mirror image of the
you and a half diagonal squares long.
are a half diagonal squares long.
needs to be two diagonal squares long.
The image of is therefore two and front.half diagonal
original, so F should look back toand a half diagonal
it D is therefore one diagonal squares
E is therefore two andhalf diagonal
G one a a
squares being a mirror image, The original shape and its
Despite beyond the mirror along the same line.
beyond the mirror along the same line.
reflection are still congruent.
More
Next

5. Explanation October 4, 2012
Here is the flag shape again.
y
4
3
2
1
x
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3
-4
This transformation is called a rotation.
To rotate a shape, you need to know…
The angle of rotation 180º
The direction of rotation anticlockwise
The centre of rotation (-2,1)
More
Next

6. Explanation October 4, 2012
The easiest way to perform a rotation is with tracing
paper.
D E
“Rotate shape DEF
F
270º anticlockwise,
0
around point 0”
Removepoint ofyour paper and join paper fixed position
Use the the tracing tracing paper the rotated
Make sure that the keep all to markupshould beatyou
Carefully trace to shape. rotations the marks shape
Unless otherwise stated,the tracingcovers both thethe
your pencil your pencil
have made. of the shape, through the tracing paper.
centrecorners
of the of rotation, whilst you
anticlockwise. of rotation. rotate it 270º.
and the centre
You can also perform a rotation by counting squares, or
by using a pair of compasses.
With the point of the compasses on the centre of
rotation, draw an arc 270º for each point.
More
Next

7. Explanation October 4, 2012
This transformation is called a translation.
Two squares down.
Three squares right.
Each point on the shape has moved the same distance,
in the same direction.
You need to describe how many squares up, or down
and how many squares left or right it has moved.
Use a single point to work this out.
Both shapes are congruent.
More
Next
End