This chapter discusses key concepts about straight lines including:
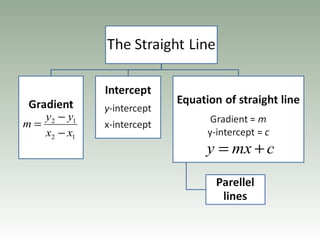
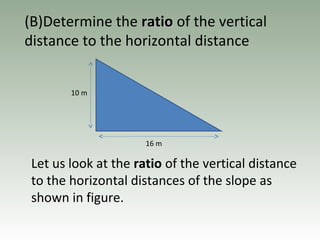
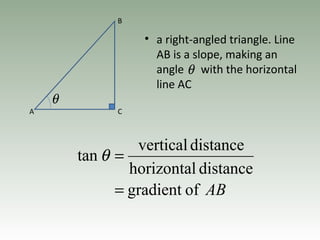
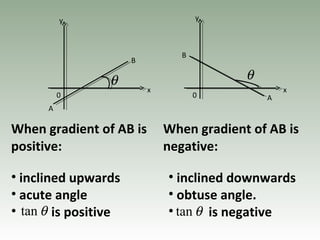
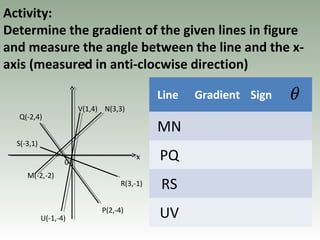
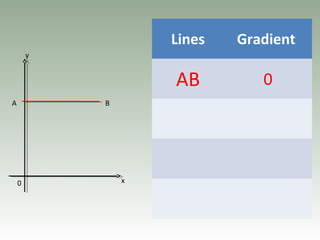
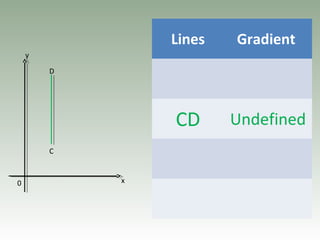
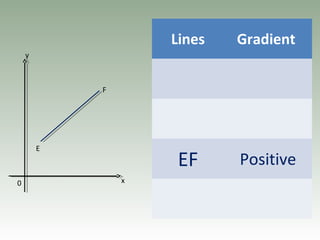
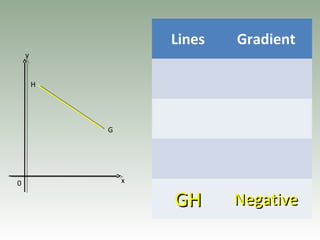
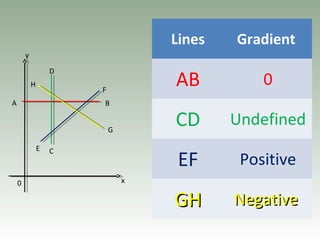
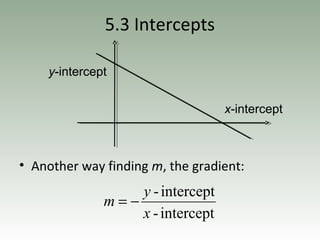
- Gradient is the ratio of vertical to horizontal distances between two points and represents the steepness of a line.
- The equation of a straight line can be written in slope-intercept form as y = mx + c or point-slope form.
- Parallel lines have the same gradient. An example shows that the lines 2x - y = 6 and 2y = 4x + 3 are parallel because they have the same gradient of 2.