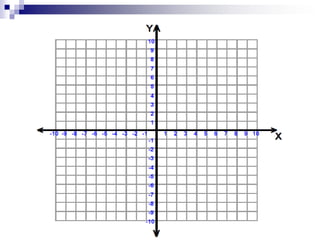
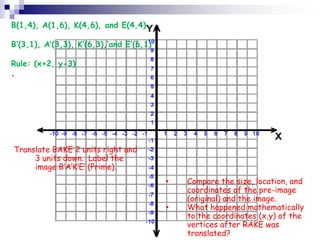
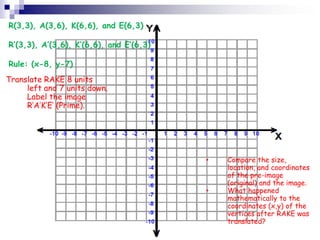
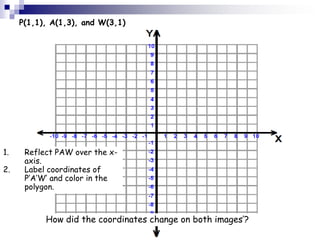
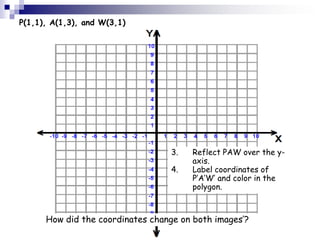
1. The document discusses different types of transformations including translations, reflections, and rotations. 2. A translation slides all points of a figure the same distance in the same direction, preserving congruence. A reflection flips a figure across a line of reflection to create a mirror image, also preserving congruence. 3. Rotations turn all points of a figure about a fixed center point through a given angle, resulting in a congruent figure. Examples are provided of applying transformations to polygons on a coordinate plane.

1. Transformations
Including Translations, Rotations and
Reflections
8G CCGPS Unit 1

2. What are Transformations?
 In mathematics, a transformation changes
the position or orientation of a figure. The
resulting figure is the image of the
original.
 Images resulting from the transformations
described in the next slides are congruent
to the original figures.

3. Vocabulary
 Translation
 Rotation
 Reflection
 Image
 Pre-Image
 Congruent
 Similar
 Angle of Rotation
 Reflection Line
 Prime
 Reflectional
symmetry
 Center of Rotation

4. Things to know
 A’ is read “A prime” and is used to
represent the point on the image that
corresponds to point A of the original
figure
 The point that a figure rotates around
may be on the figure or away from the
figure.

6. Translations
Translation
The figure slides along a straight line without
turning.

7. Working With Translations
1. Plot polygon BAKE on a coordinate plane using
vertices B(1,4), A(1,6), K(4,6), and E(4,4).
2. Label the coordinates and connect the
vertices.
3. Color in the polygon.
4. Translate BAKE 2 units right and 3 units down.
Label the image B’A’K’E’ (Prime).
5. Compare the size, location, and coordinates of
the pre-image (original) and the image.
6. What happened mathematically to the
coordinates (x,y) of the vertices after BAKE
was translated?

8. B(1,4), A(1,6), K(4,6), and E(4,4)
B’(3,1), A’(3,3), K’(6,3),’and E’(6,1)
Rule: (x+2, y-3)
.
Translate BAKE 2 units right and
3 units down. Label the
image B’A’K’E’ (Prime).
• Compare the size, location, and
coordinates of the pre-image
(original) and the image.
• What happened mathematically
to the coordinates (x,y) of the
vertices after RAKE was
translated?

9. Working With Translations
1. Plot polygon RAKE on a coordinate plane using
vertices R(3,3), A(3,6), K(6,6), and E(6,3).
2. Label the coordinates and connect the
vertices.
3. Color in the polygon.
4. Translate RAKE 8 units left and 7 units down
and. Label the image R’A’K’E’ (Prime).
5. Compare the size, location, and coordinates of
the pre-image (original) and the image.
6. What happened mathematically to the
coordinates (x,y) of the vertices after RAKE
was translated?

10. R(3,3), A(3,6), K(6,6), and E(6,3)
R’(3,3), A’(3,6), K’(6,6), and E’(6,3)
Rule: (x-8, y-7)
Translate RAKE 8 units
left and 7 units down.
Label the image
R’A’K’E’ (Prime).
• Compare the size,
location, and coordinates
of the pre-image
(original) and the image.
• What happened
mathematically to the
coordinates (x,y) of the
vertices after RAKE was
translated?

11. Reflections
Reflection
The figure flips across a line of
reflection, creating a mirror image.

12. Working With Reflections
1. Plot polygon PAW on a coordinate plane using
vertices P(1,1), A(1,3), and W(3,1).
2. Label coordinates and connect the vertices.
3. Color in the polygon.
4. Reflect PAW over the x-axis.
5. Label coordinates of P’A’W’ and color in the polygon.
6. How did the coordinates change on the image
C’A’K’E’?

13. P(1,1), A(1,3), and W(3,1)
1. Reflect PAW over the x-
axis.
2. Label coordinates of
P’A’W’ and color in the
polygon.
How did the coordinates change on both images’?

14. Working With Reflections
1. Plot polygon PAW on a coordinate plane using
vertices P(1,1), A(1,3), and W(3,1).
2. Label coordinates and connect the vertices.
3. Color in the polygon.
4. Reflect PAW over the y-axis.
5. Label coordinates of P’A’W’ and color in the polygon.
6. How did the coordinates change on the image
P’A’W’?

15. P(1,1), A(1,3), and W(3,1)
3. Reflect PAW over the y-
axis.
4. Label coordinates of
P’A’W’ and color in the
polygon.
How did the coordinates change on both images’?

16. Reflection Rule
To reflect along the x-
axis:
• x stays the same
• y is its opposite
• Example: (3,-2) = (3,2)
Pre-image WOLF
 W(3,3)
 O(3,6)
 L(8,6)
 F(8,3)
Image W’O’L’F’
 W’(3,-3)
 O’(3,-6)
 L’(8,-6)
 F’(8,-3)

17. Reflection Rule
To reflect along the y-
axis:
 y stays the same
 x is its opposite
 Example: (3,-2) = (-3,-2)
Pre-image WOLF
 W(3,3)
 O(3,6)
 L(8,6)
 F(8,3)
Image W’O’L’F’
 W’(-3,3)
 O’(-3,6)
 L’(-8,6)
 F’(-8,3)

18. Transformations
 The mapping, or movement, of all the
points of a figure in a plane according to
a common operation.
 A change in position occurs in
translations, reflections and rotations.

19. Translation (slide)
 A transformation that “slides” each
point of a figure the same distance in
the same direction.
 A translation will be a congruent figure.
 Example:

20. Reflection (flip)
 A transformation that “flips” a figure
over a line of reflection.
 A mirror image is created.
 A reflection will be a congruent figure.
 Example:

21. Rotation (turn)
 A transformation that turns a figure
about a fixed point through a given
angle and a given direction.
 A rotation will be a congruent figure.
 Example: