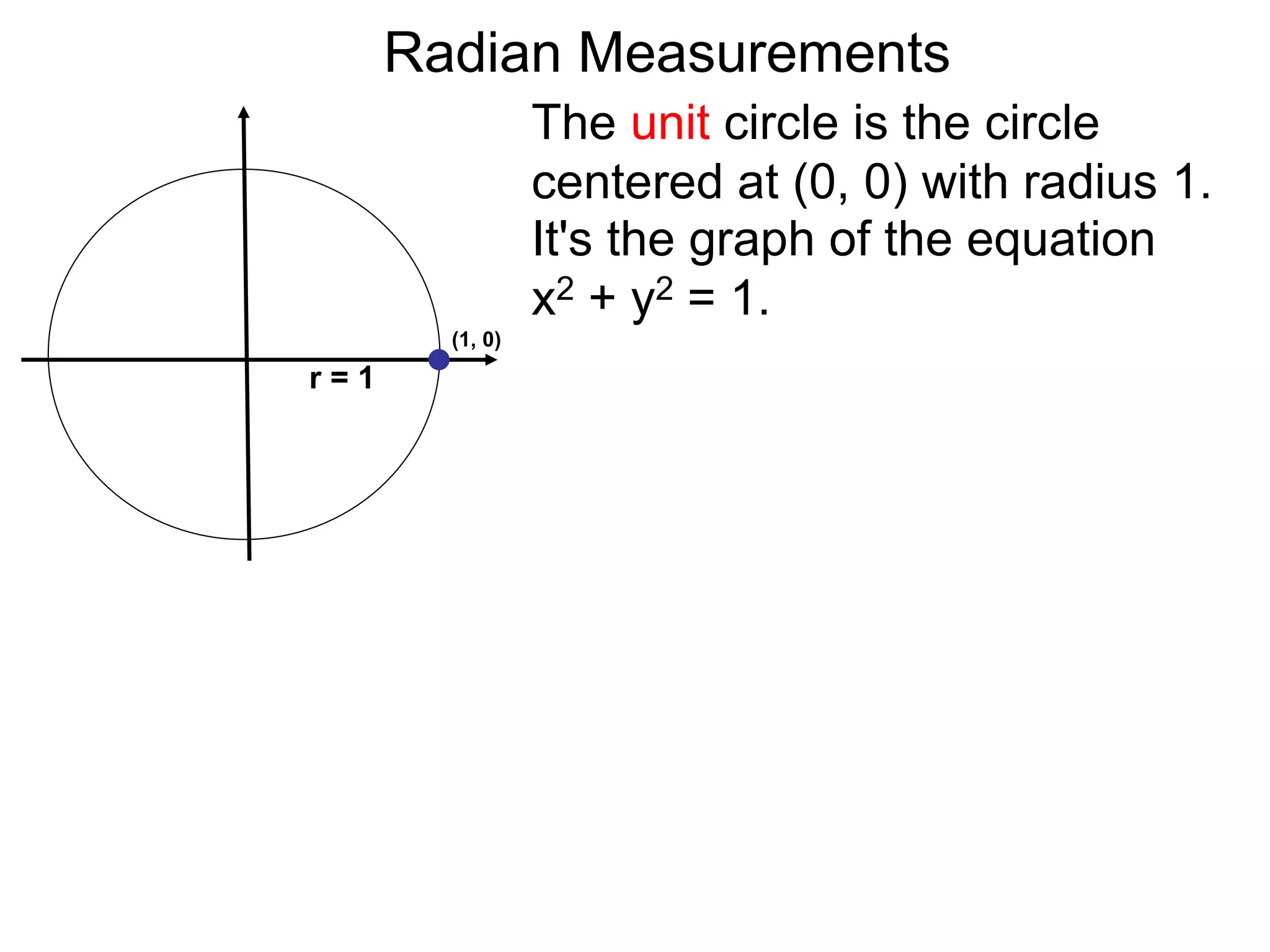
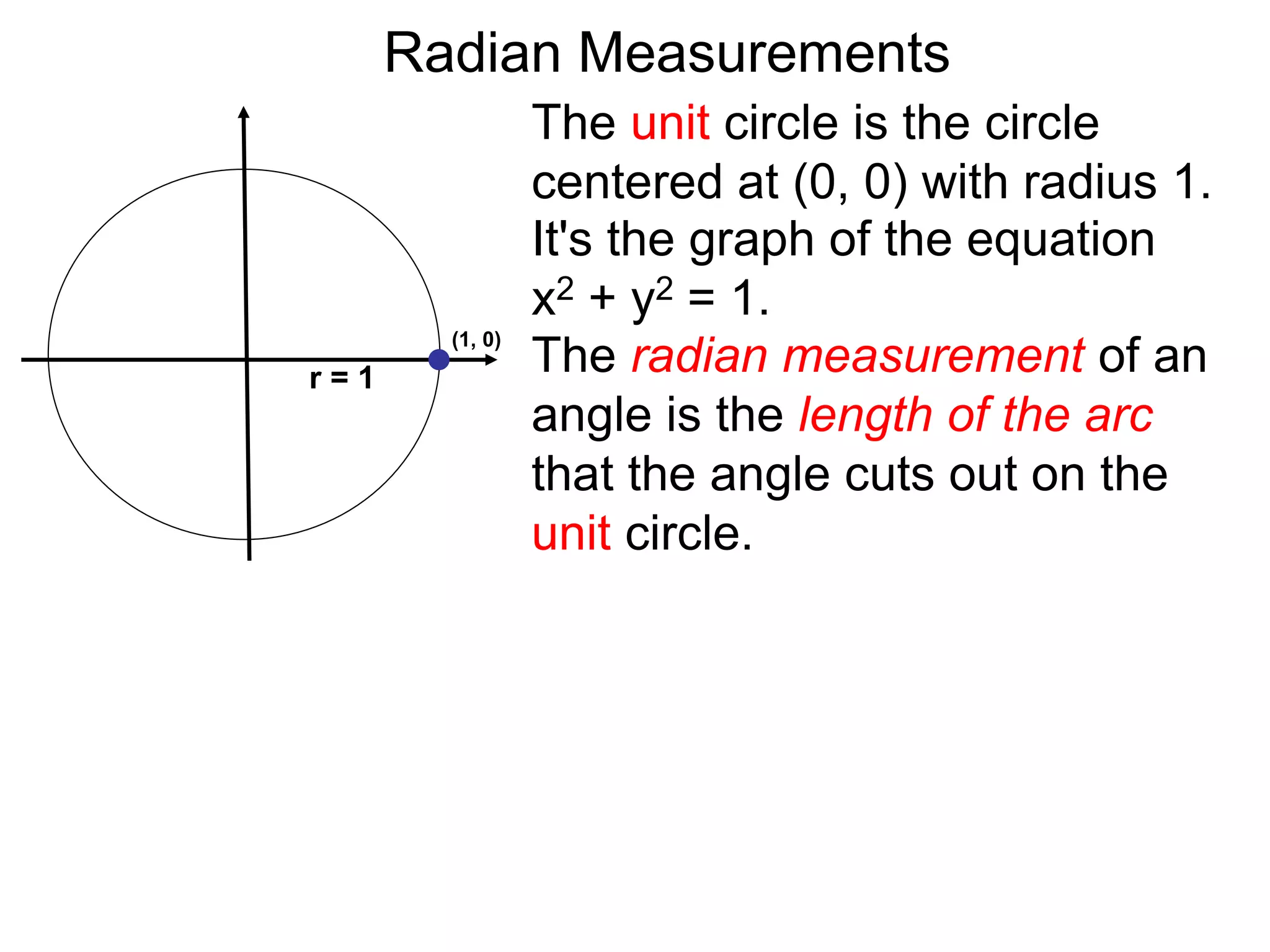
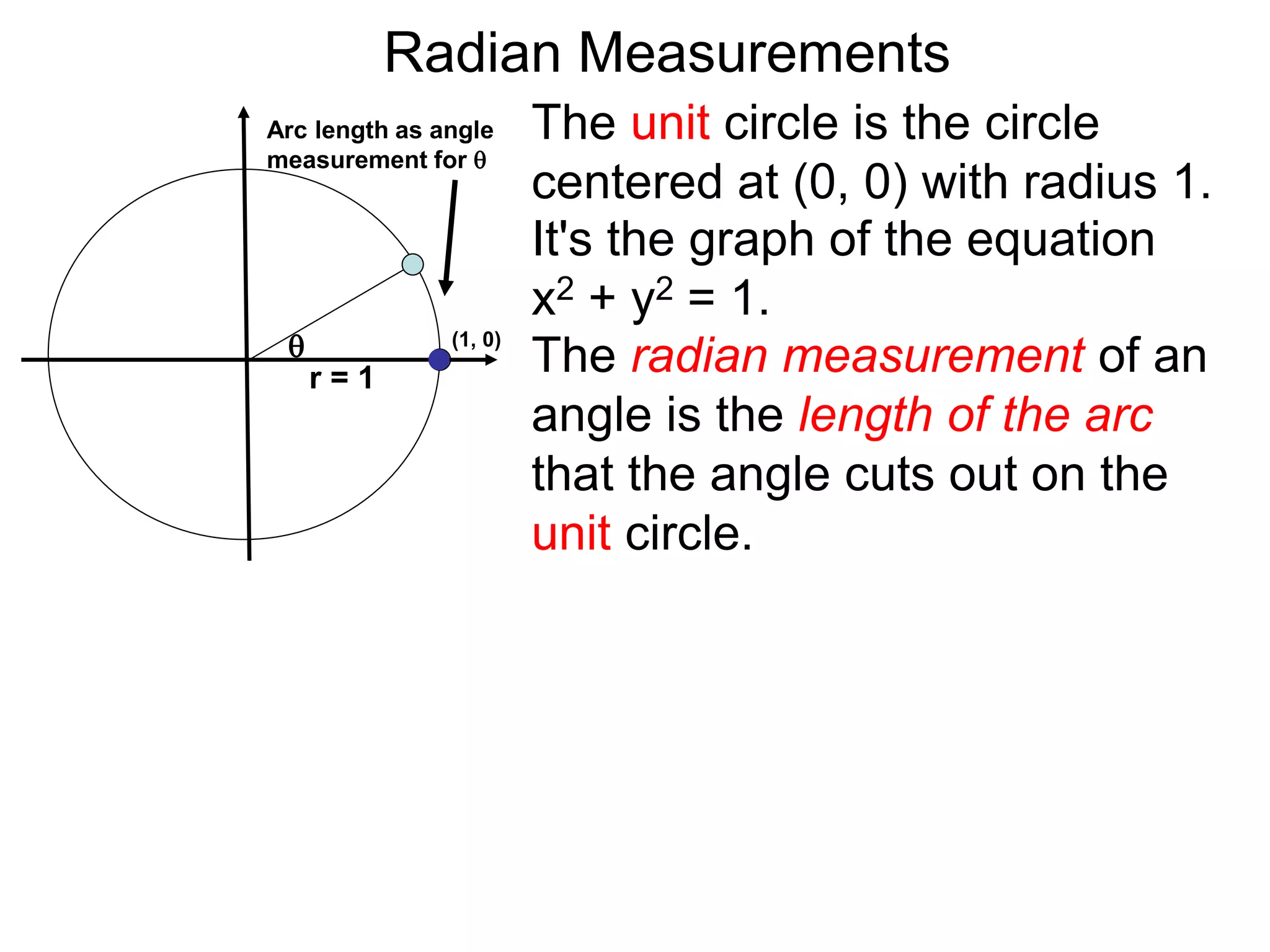
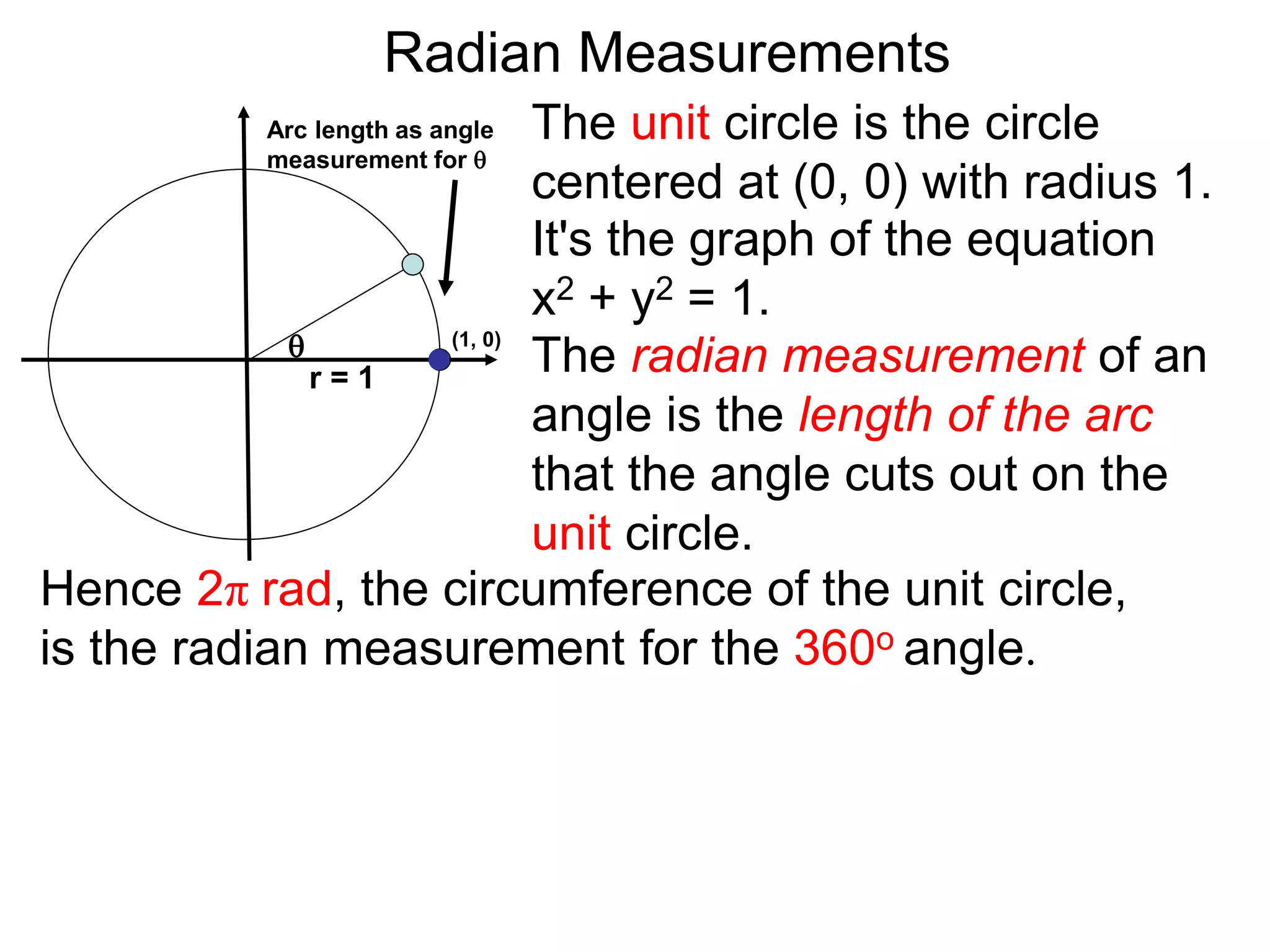
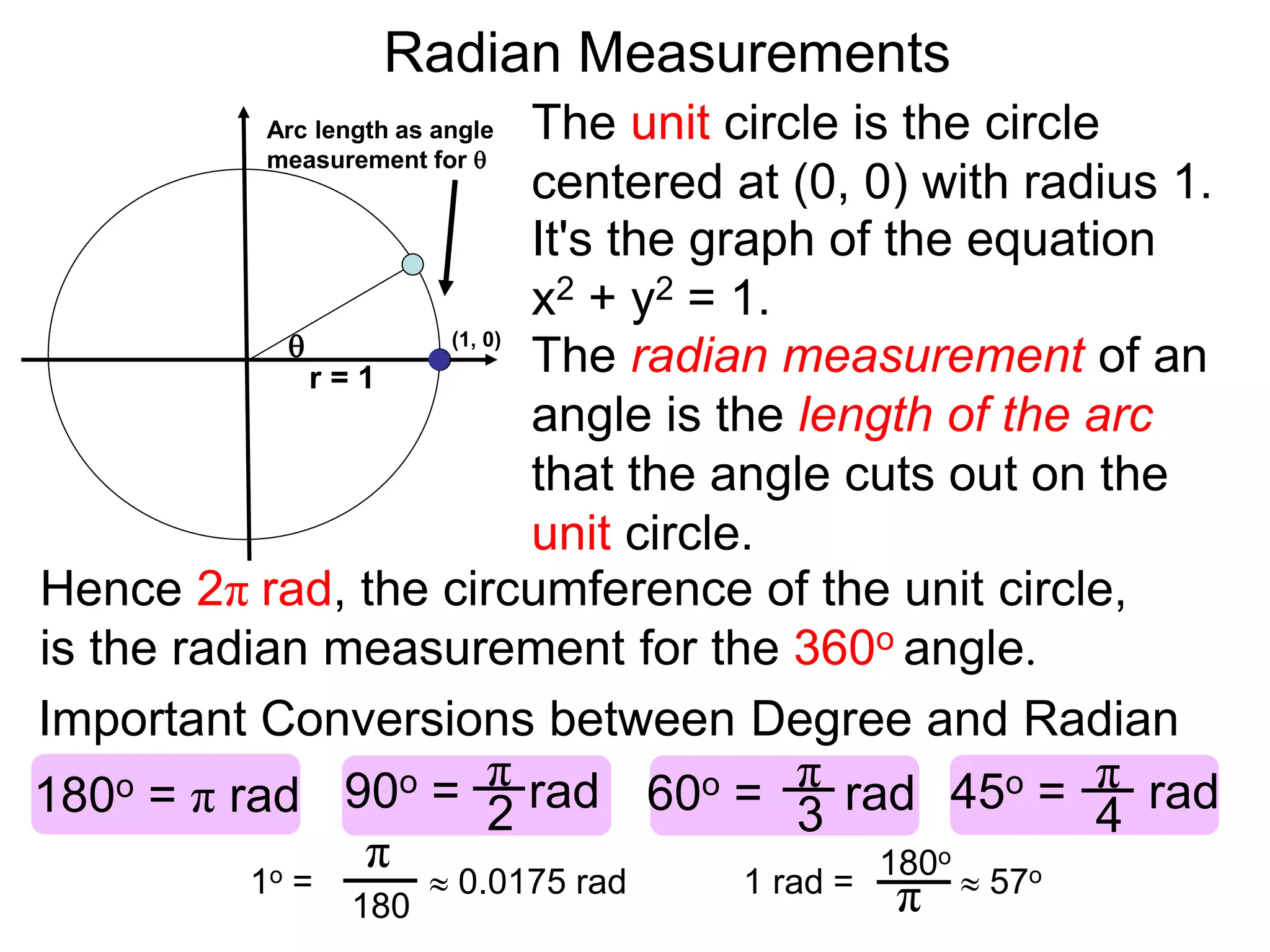
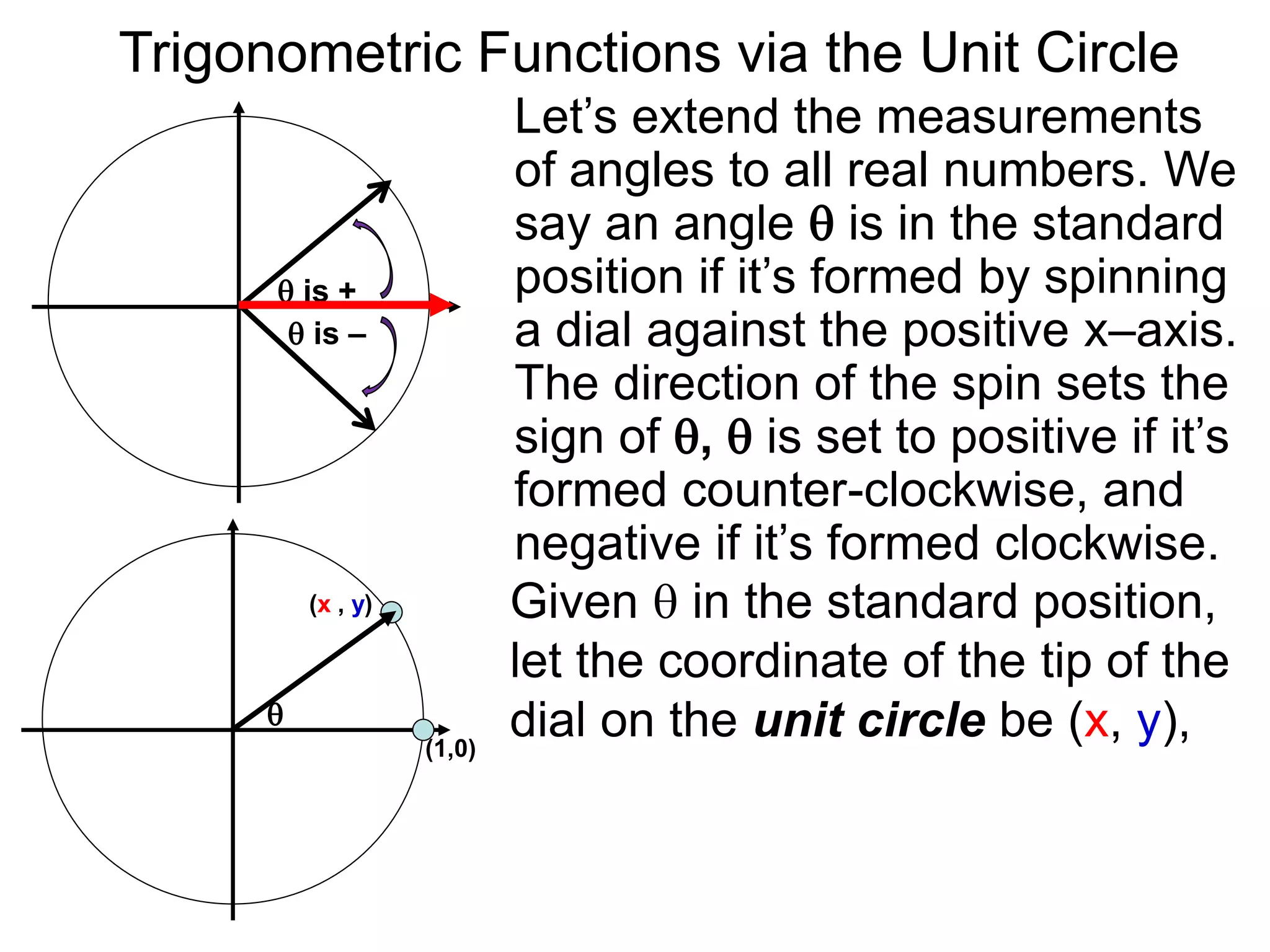
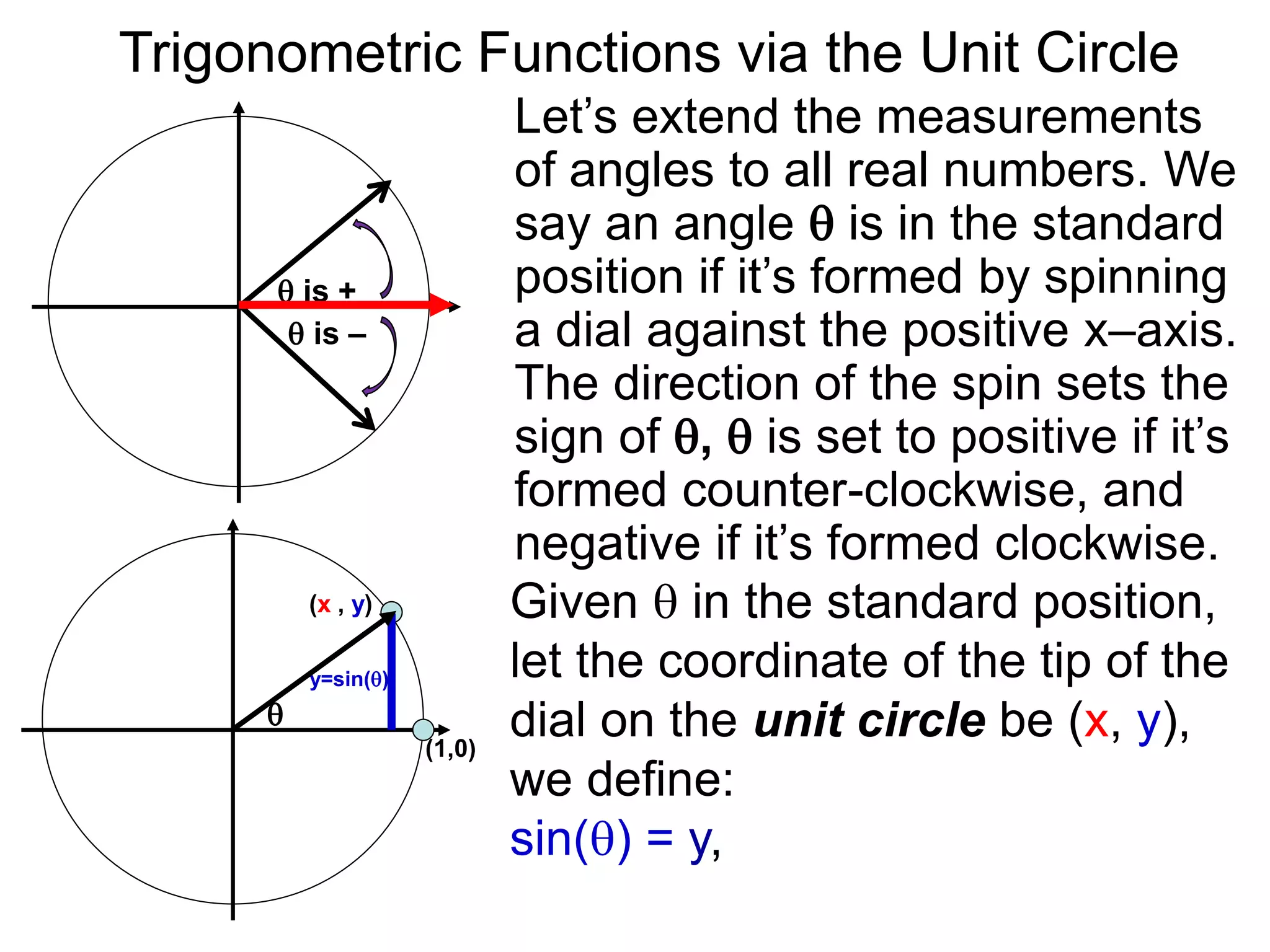
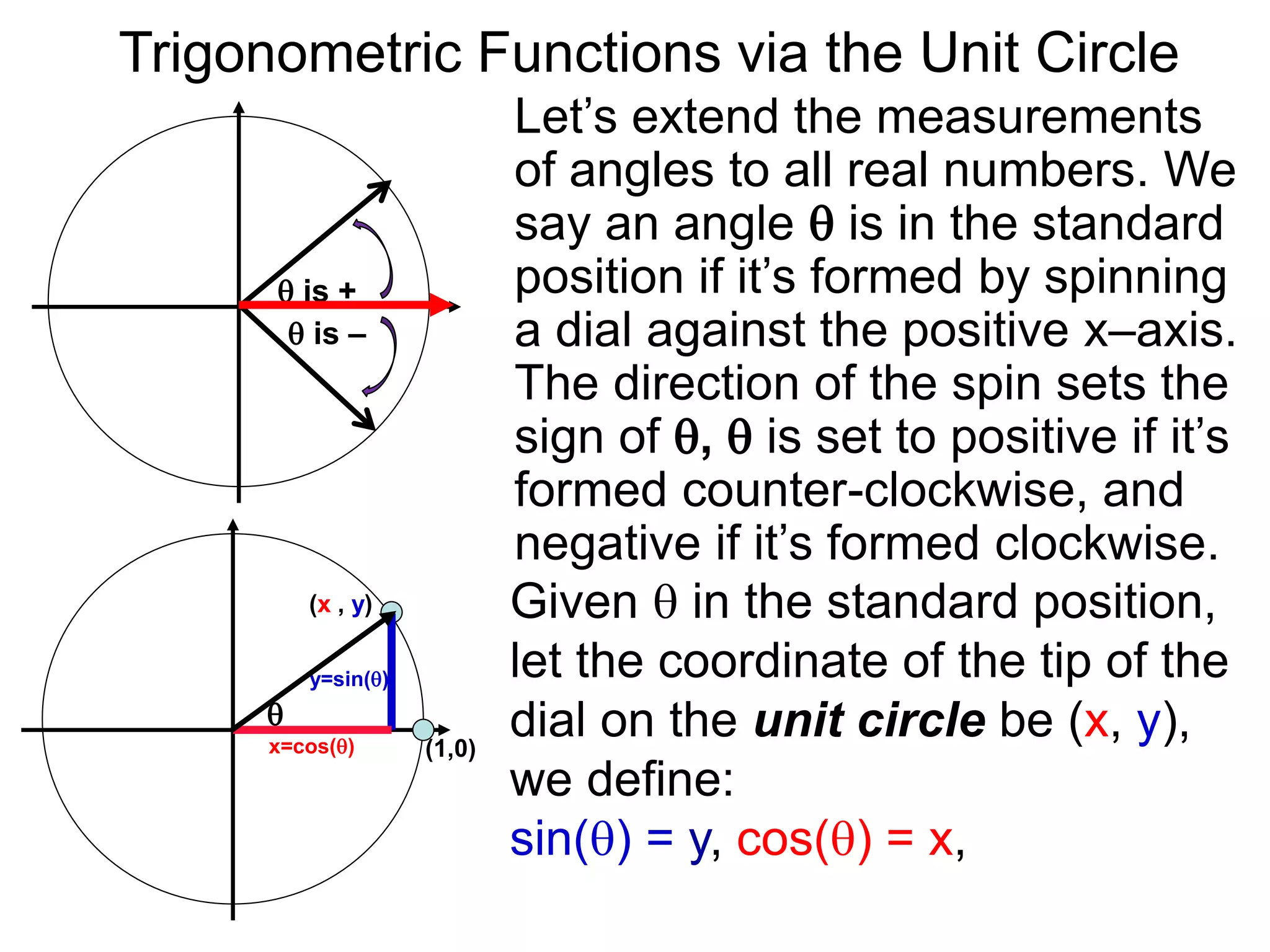
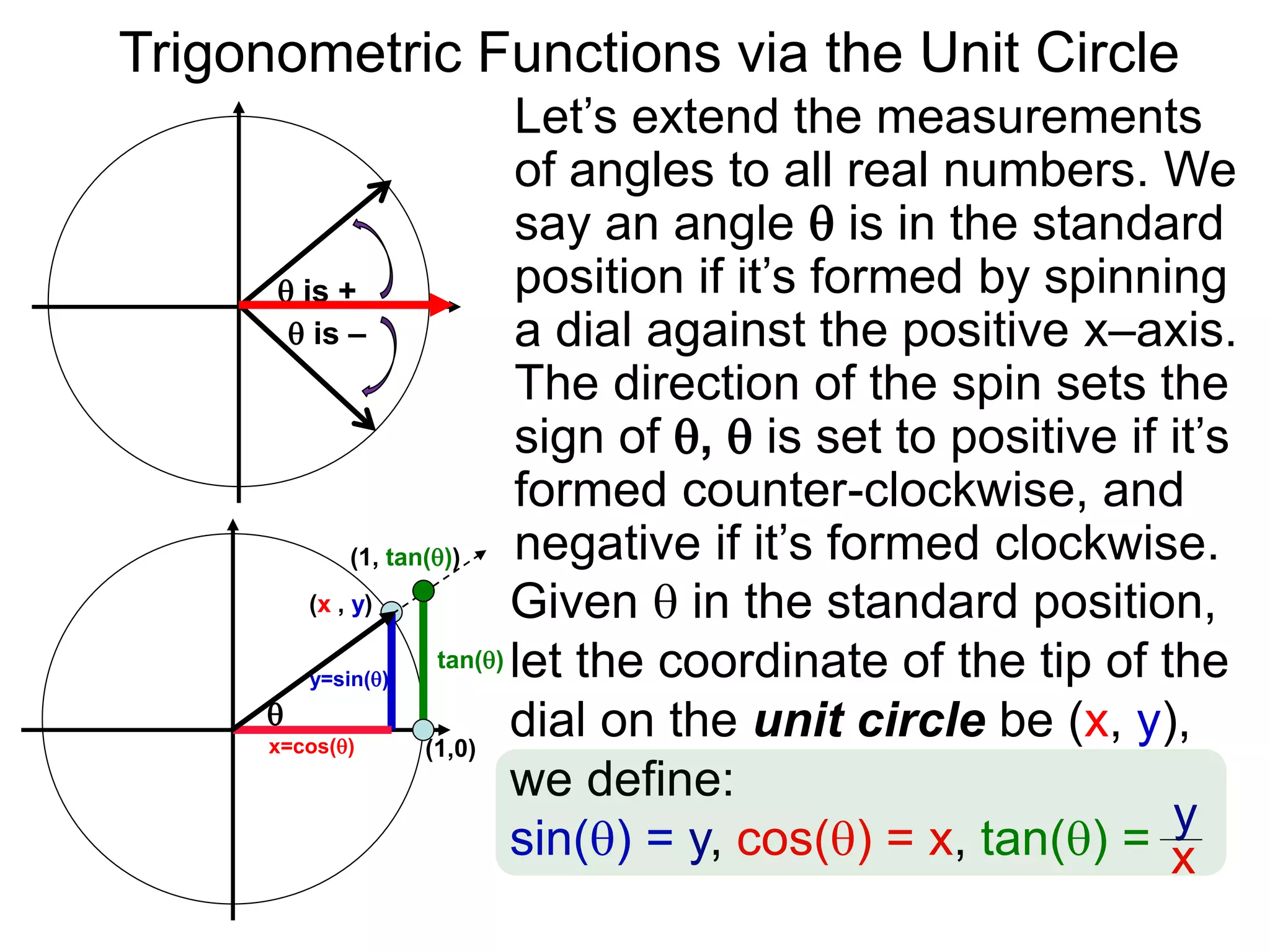
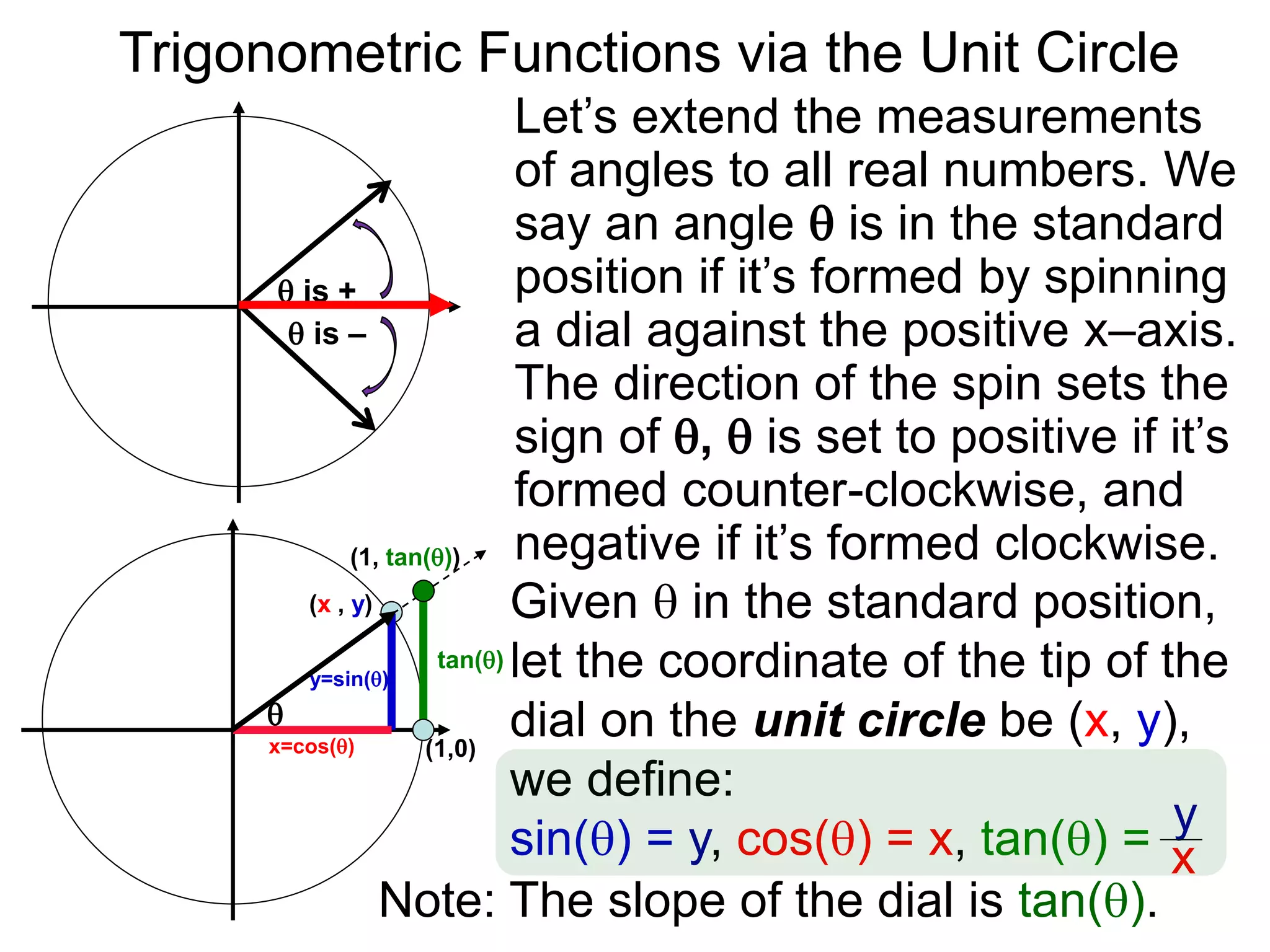
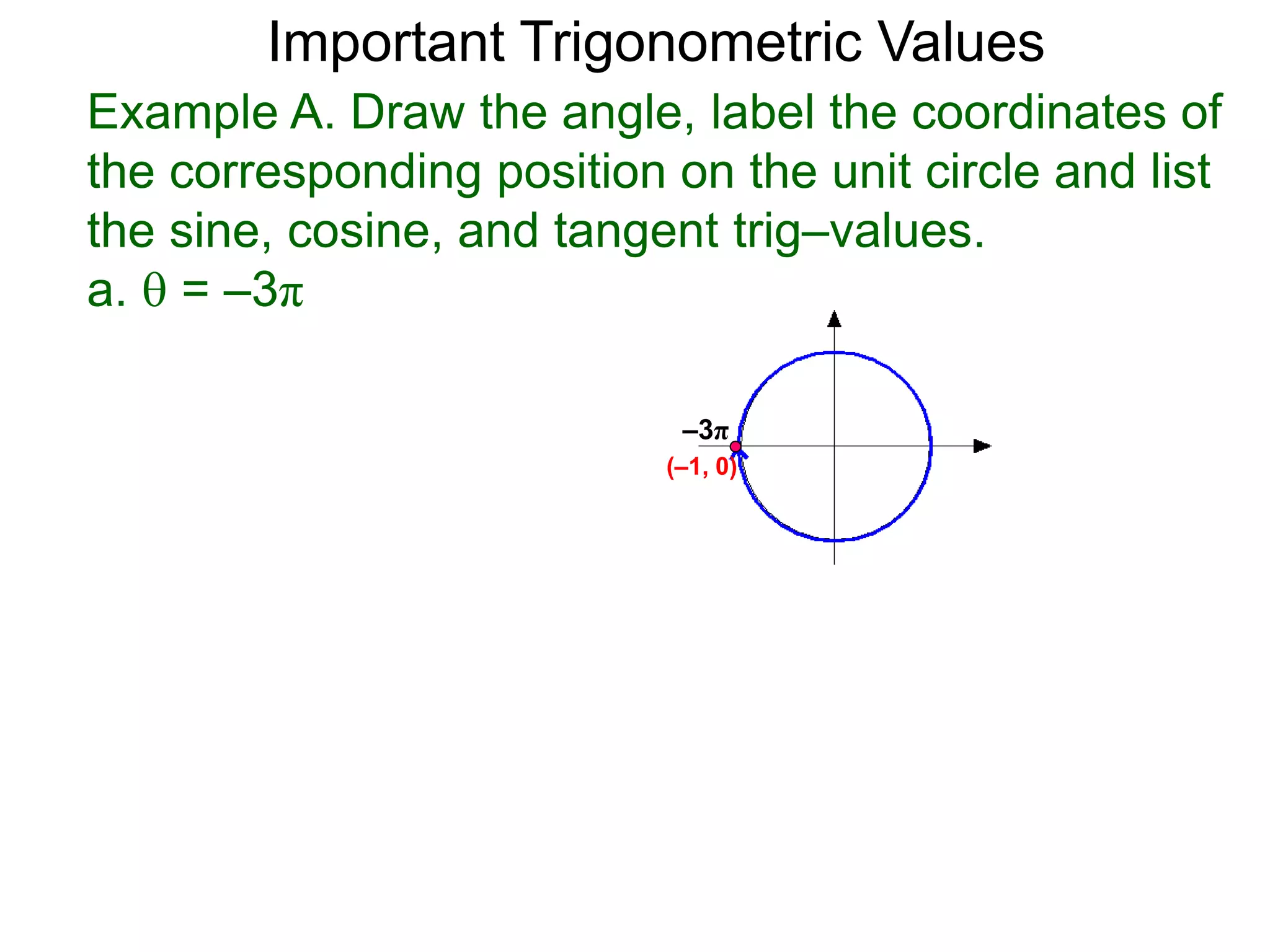
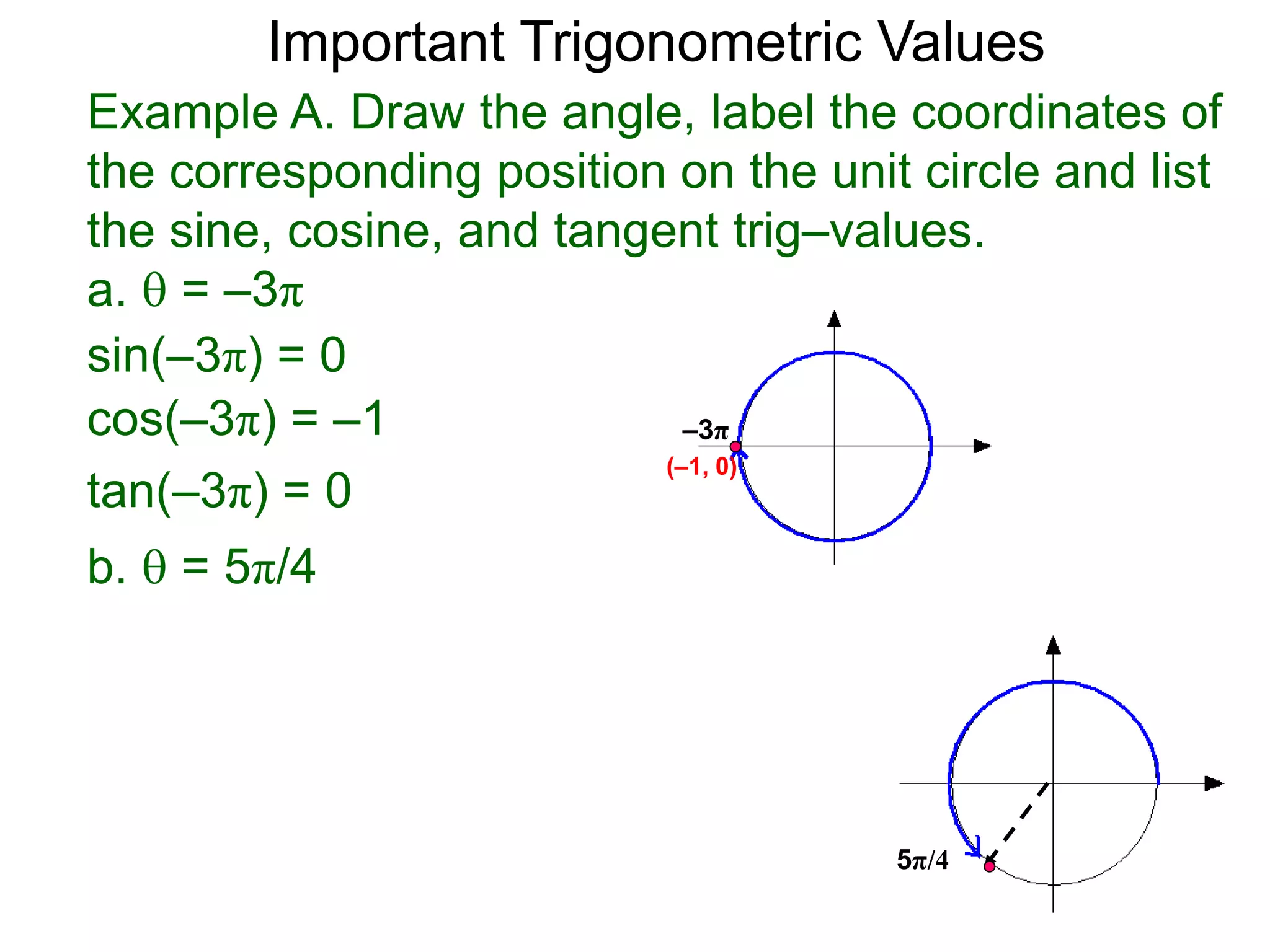
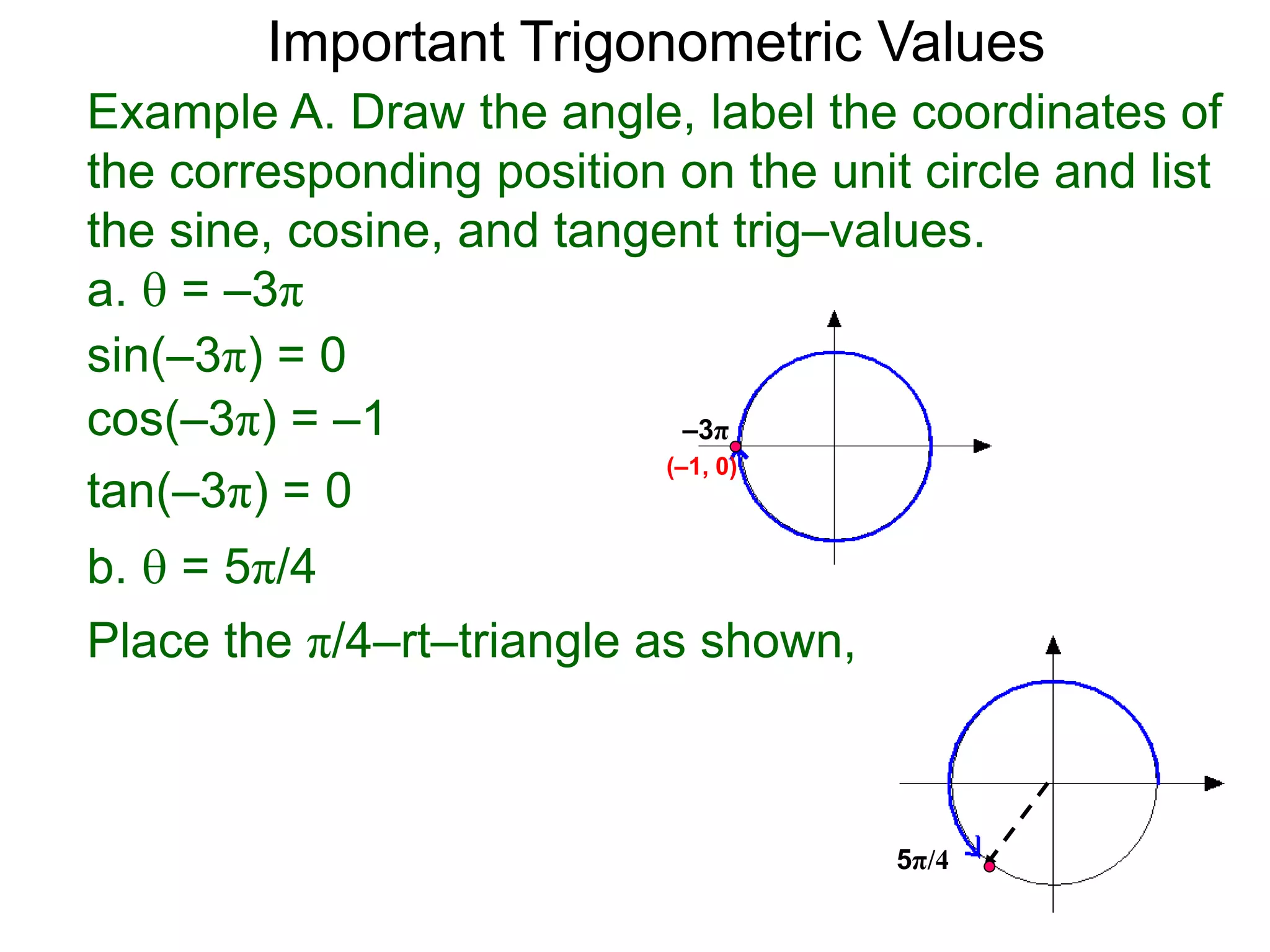
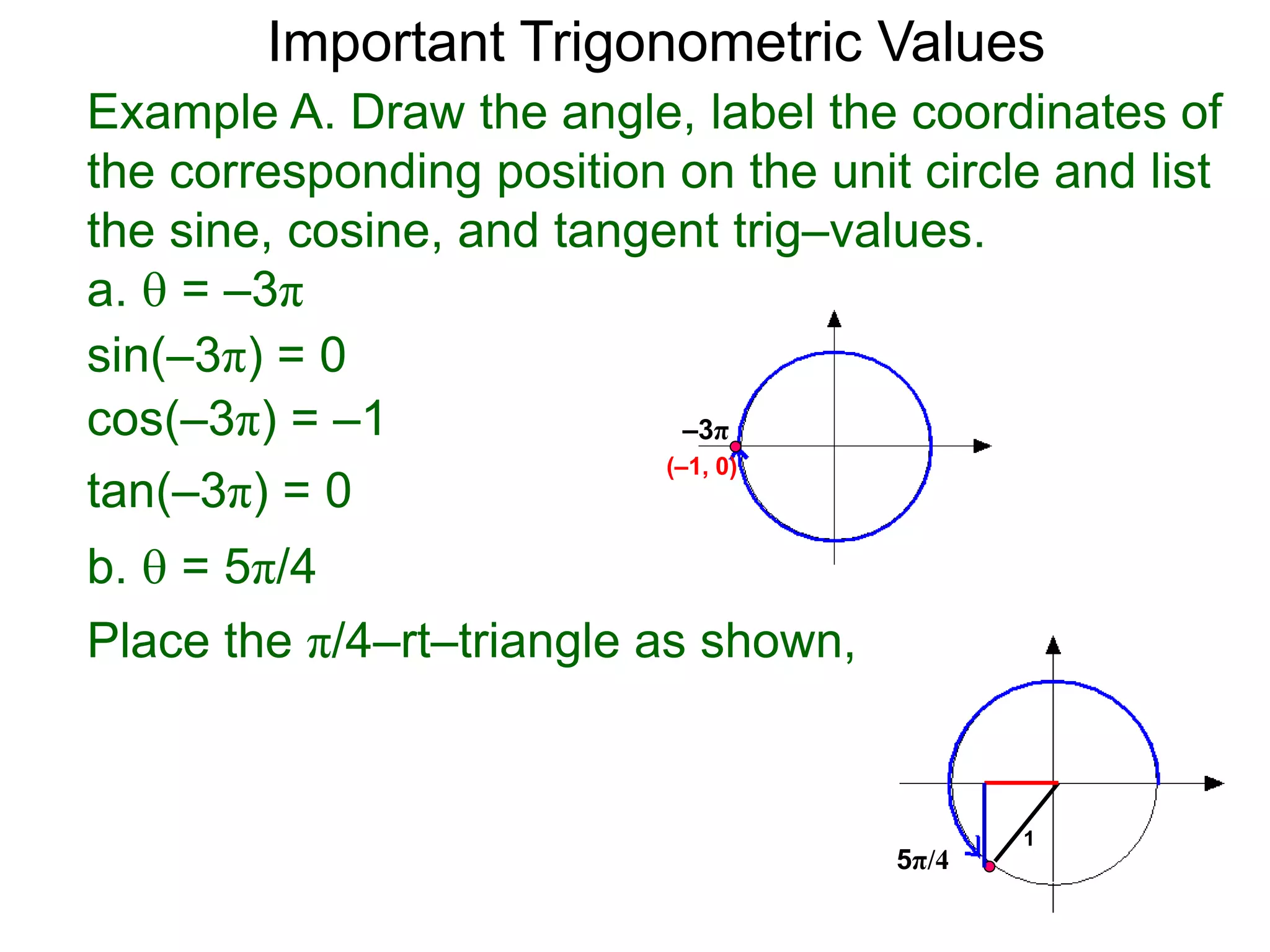
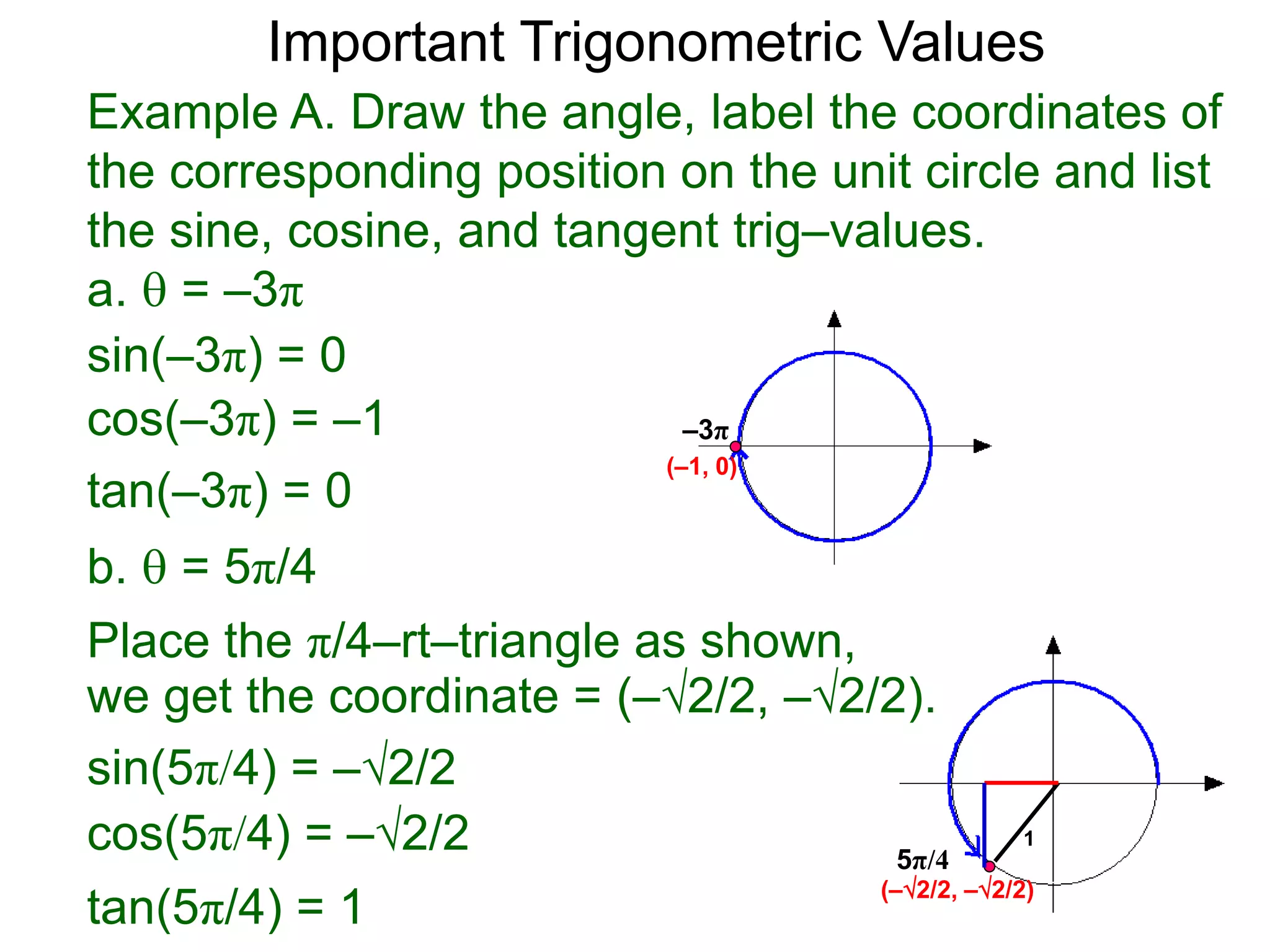
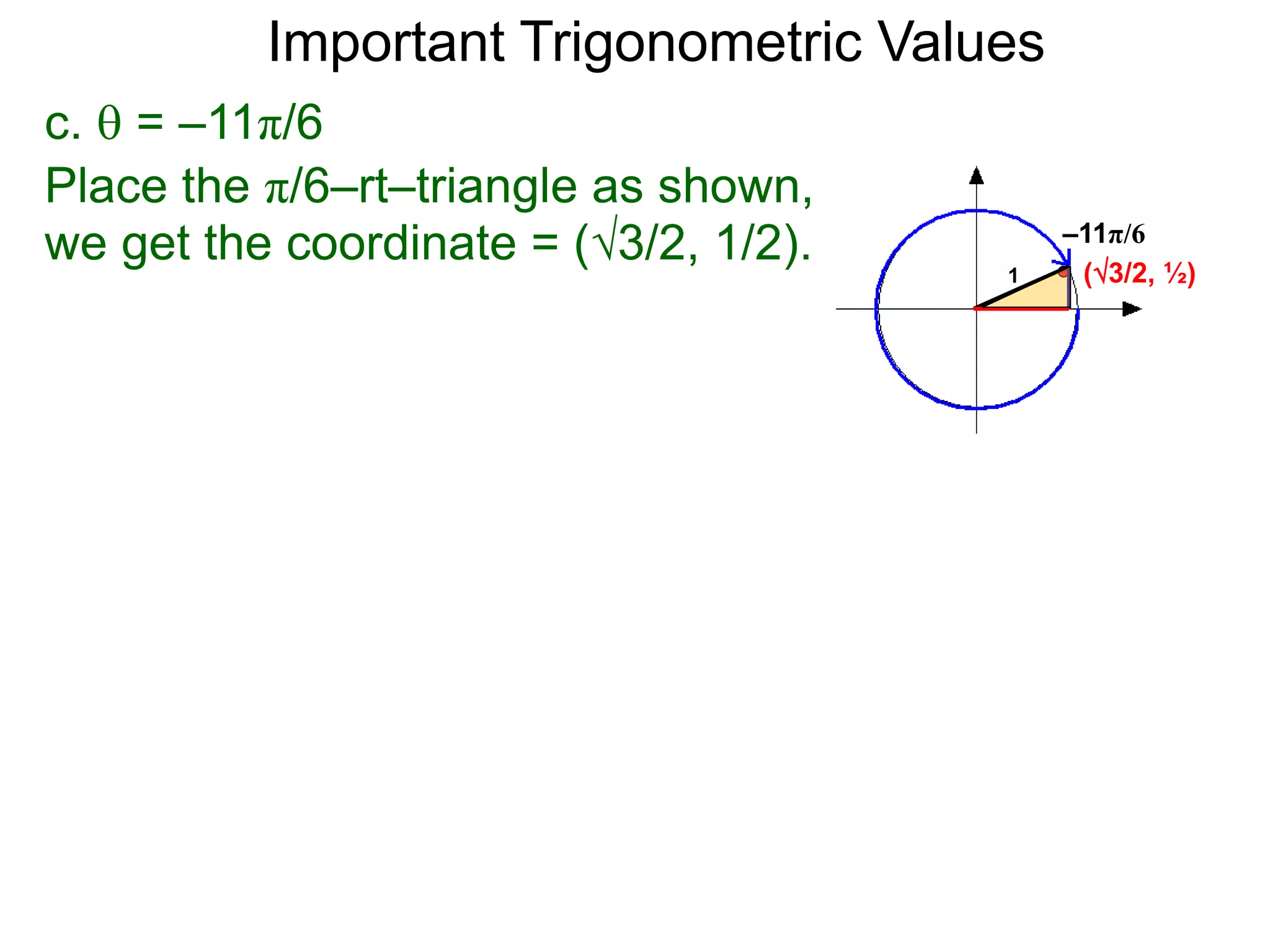
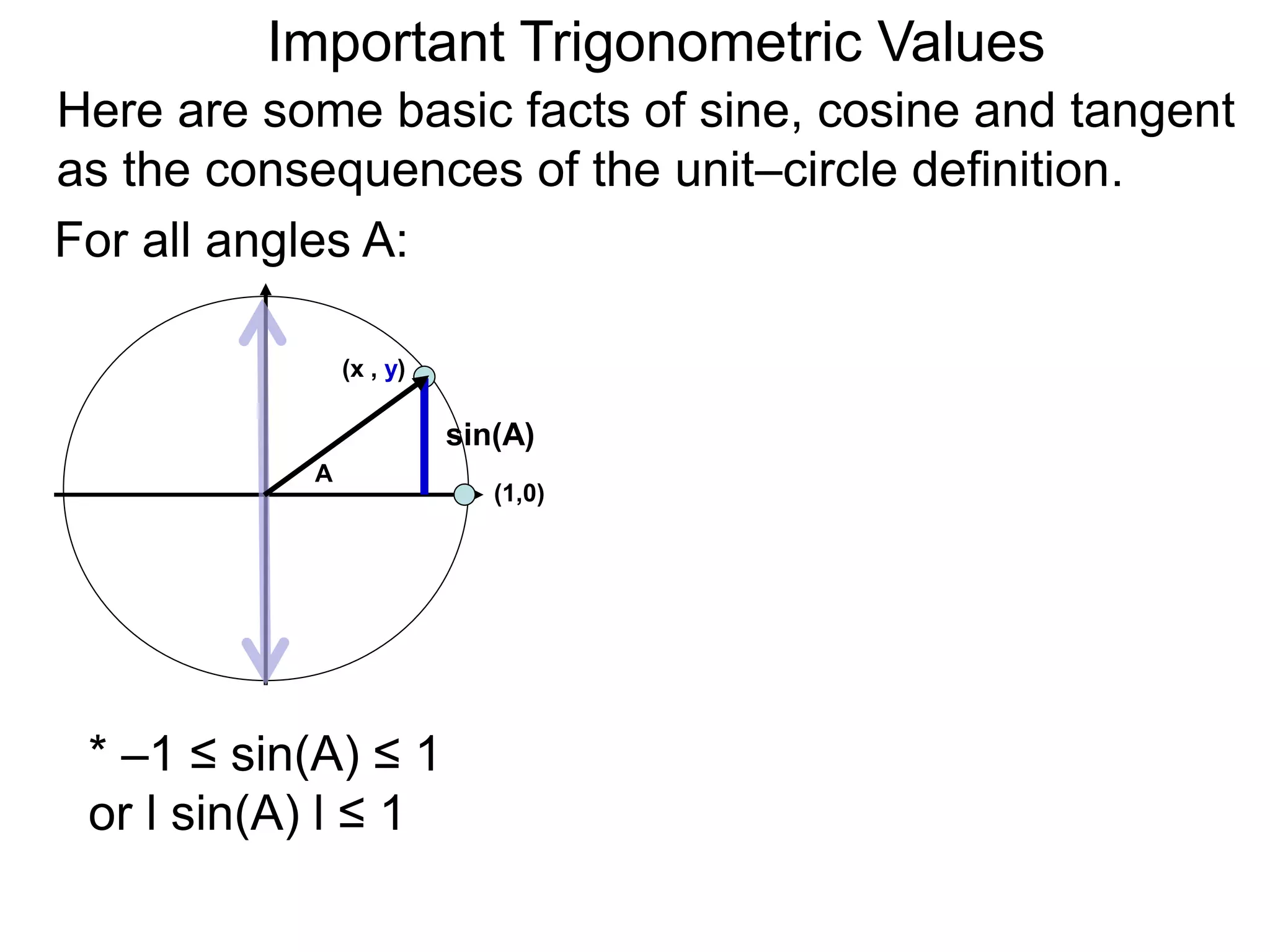
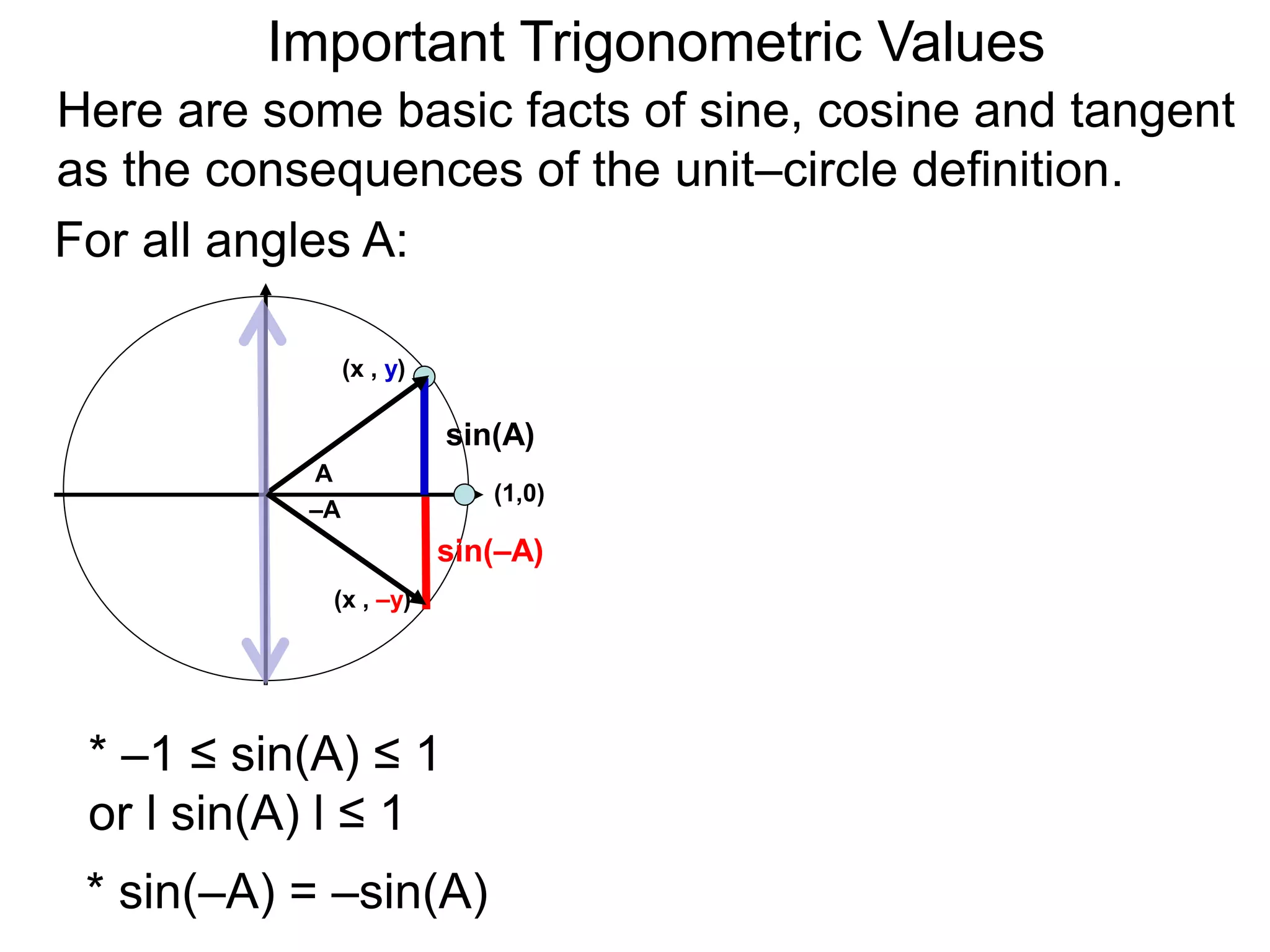
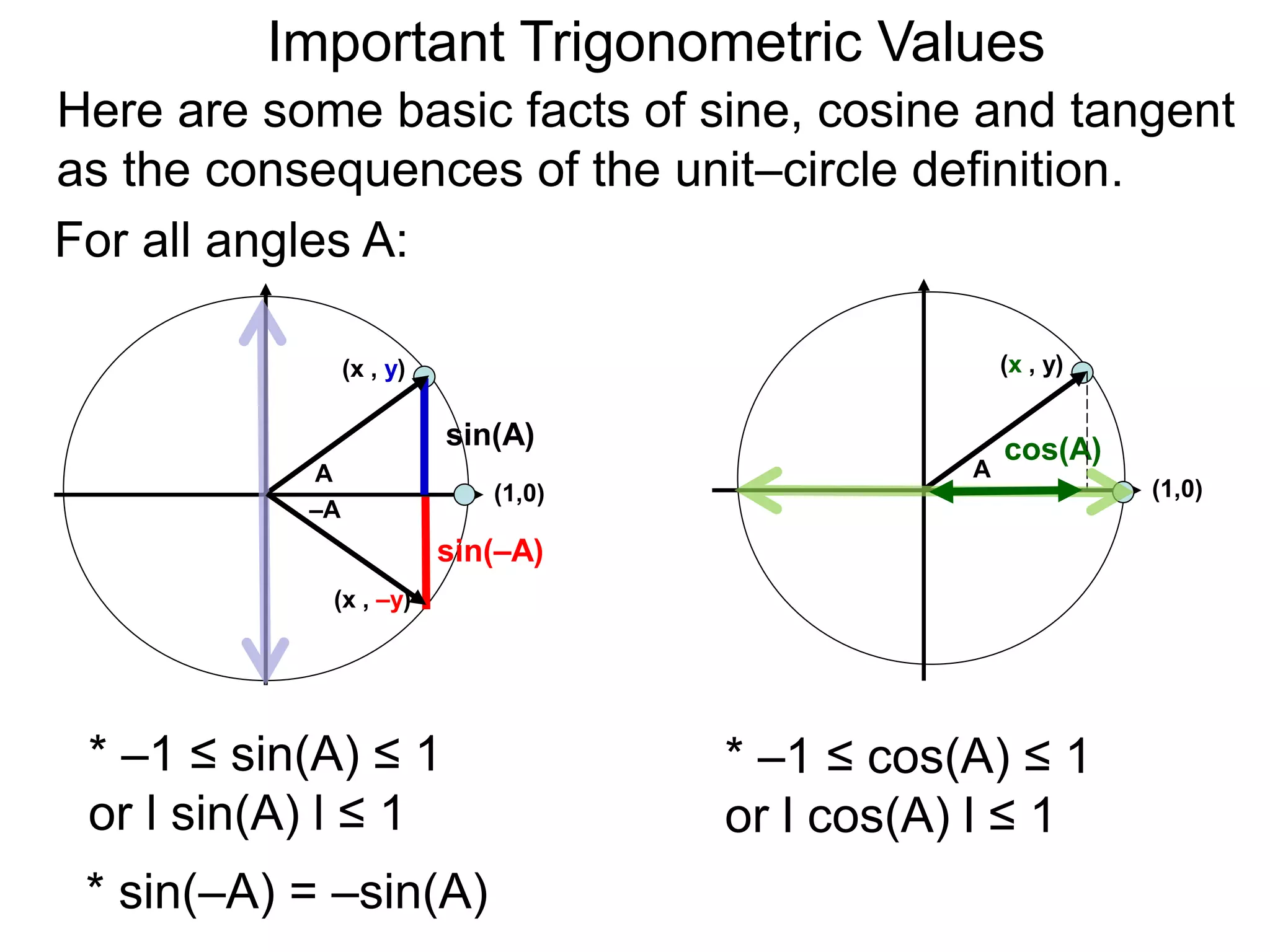
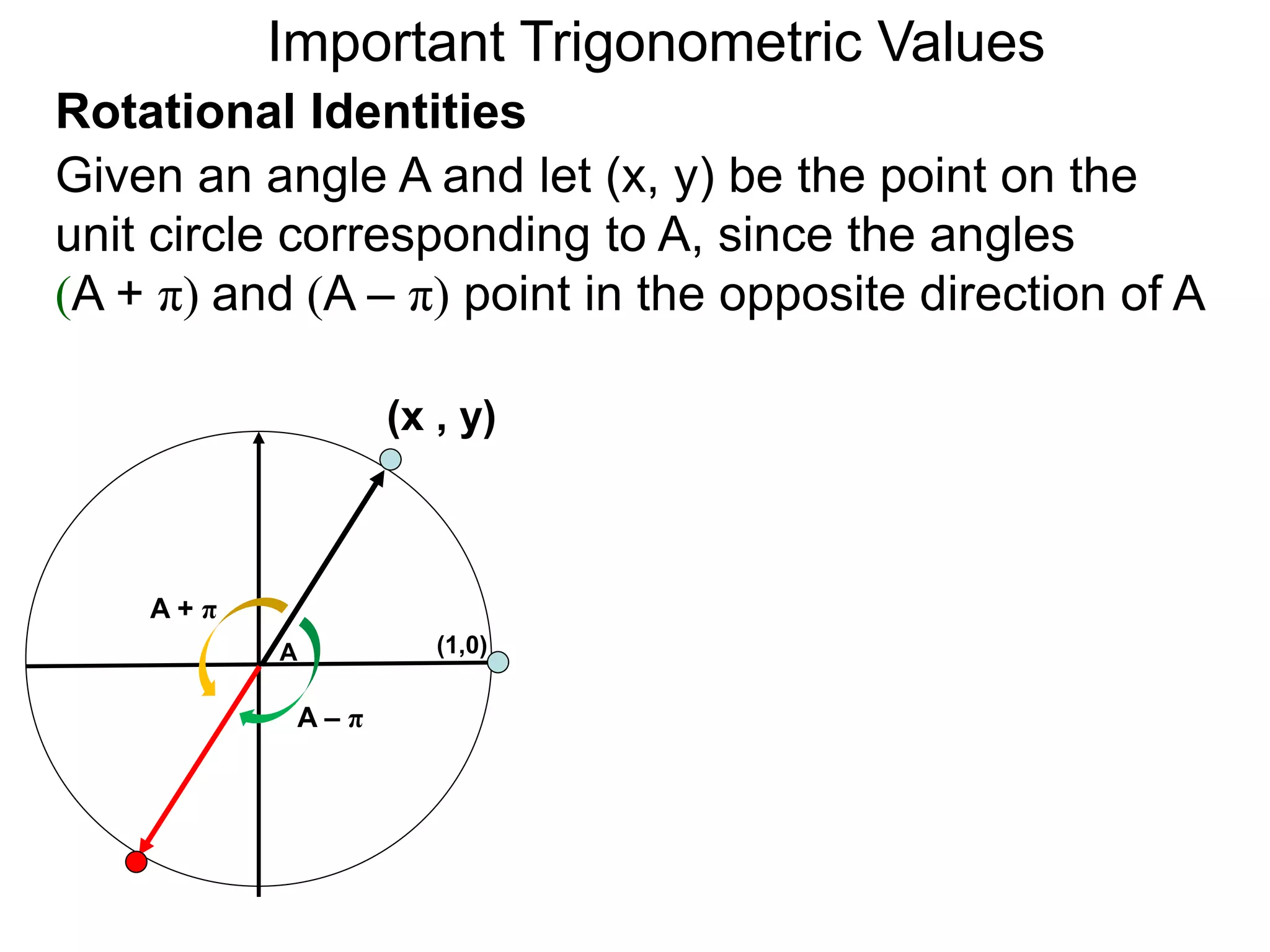
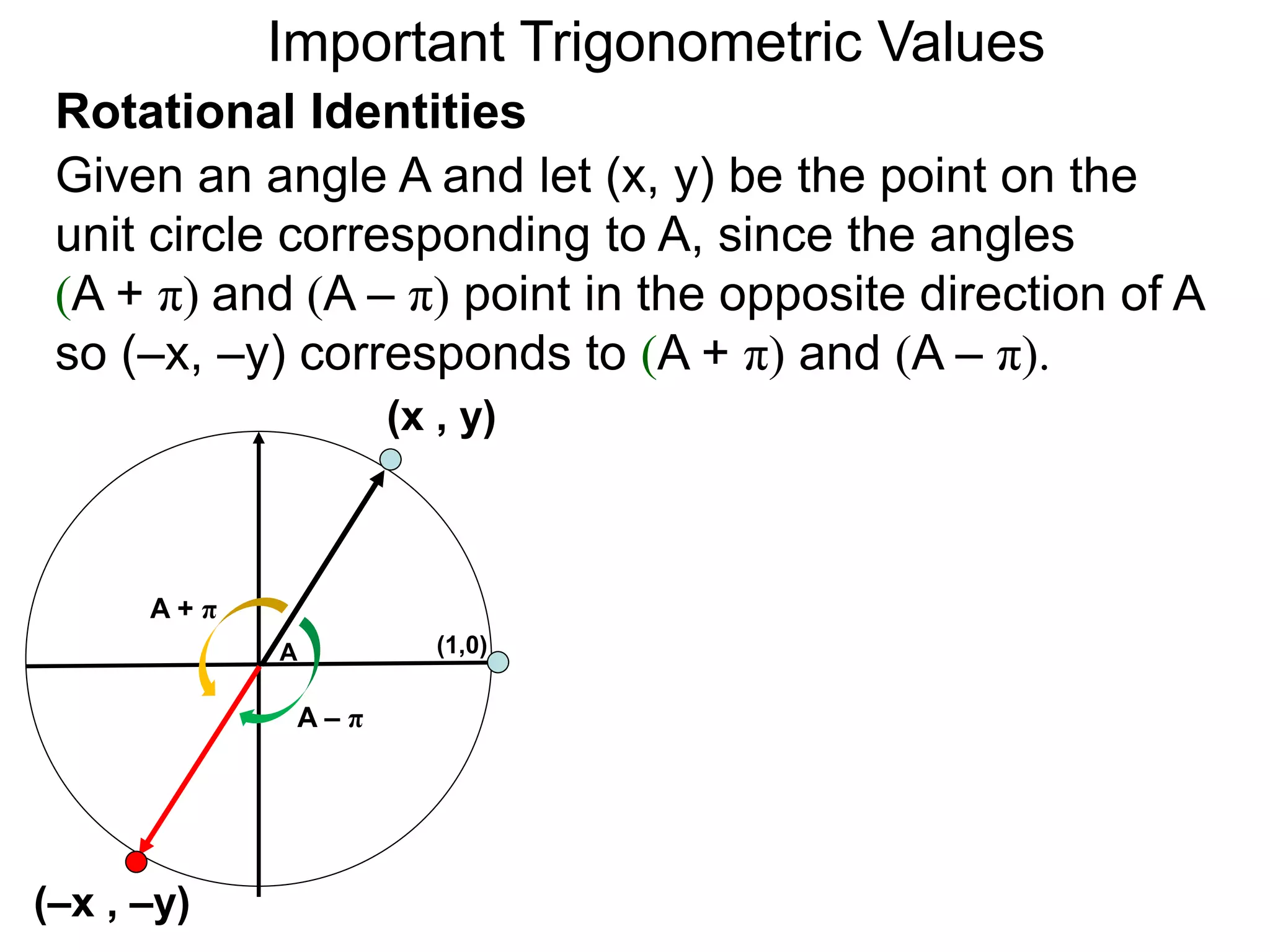
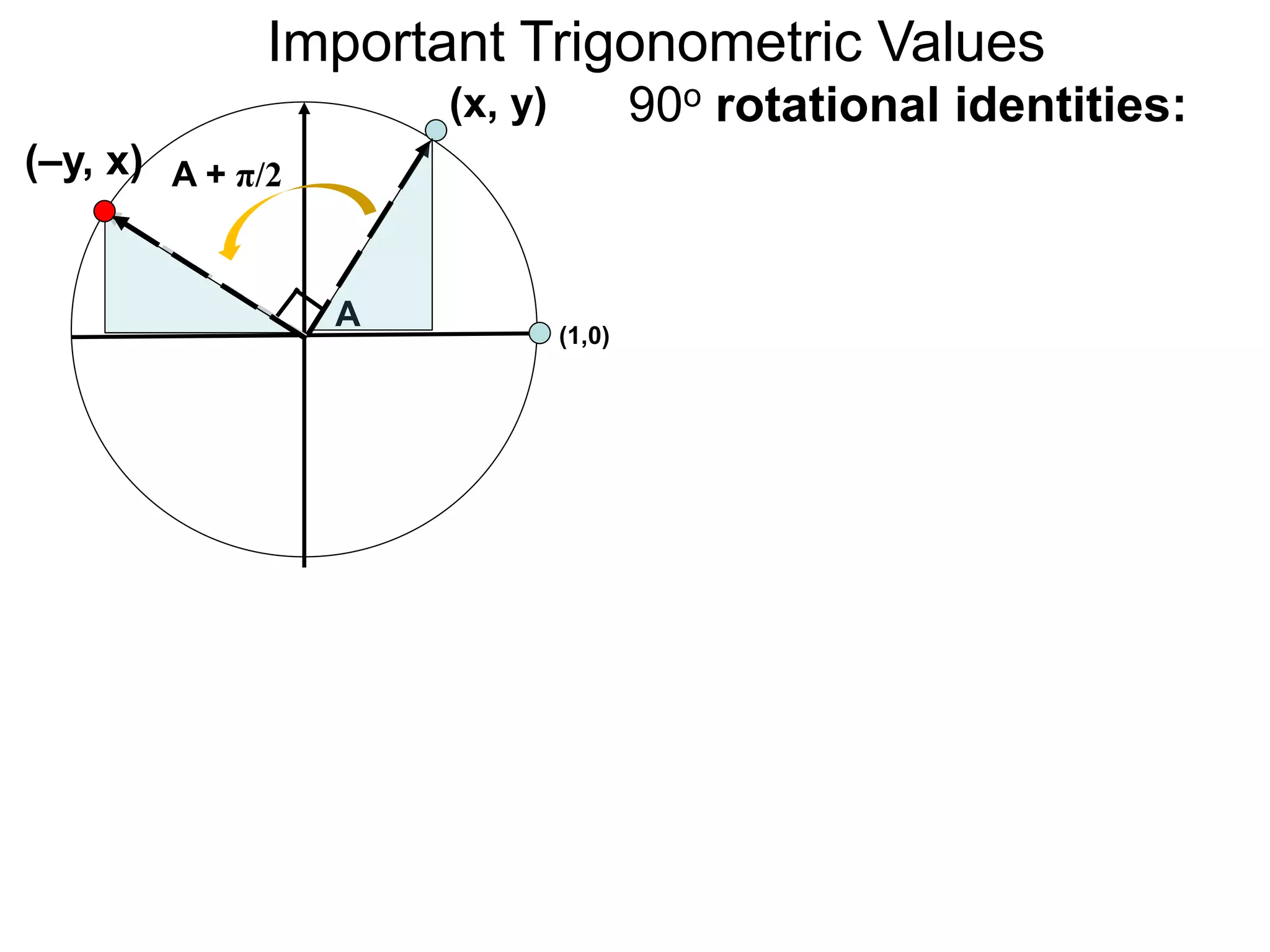
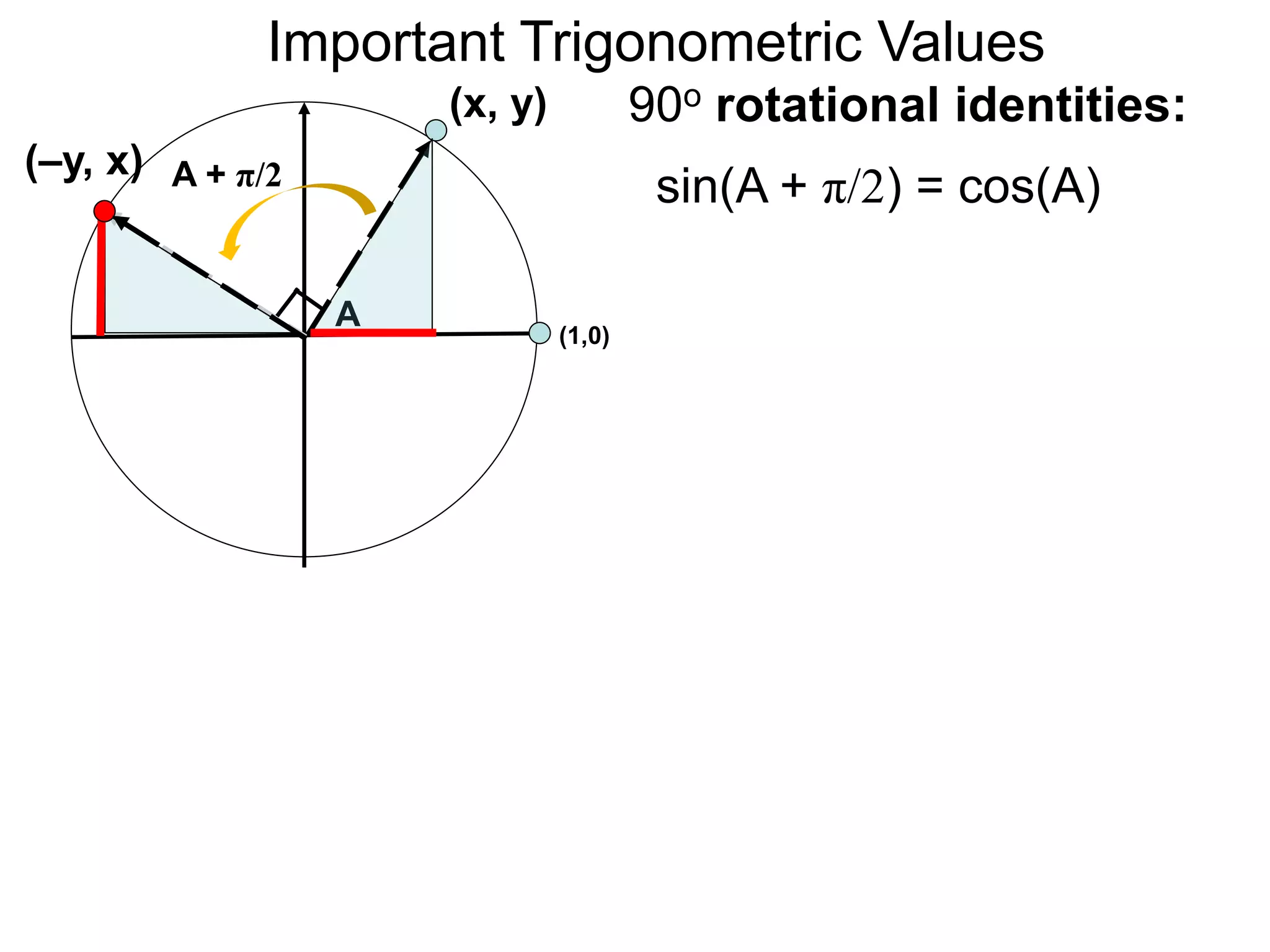
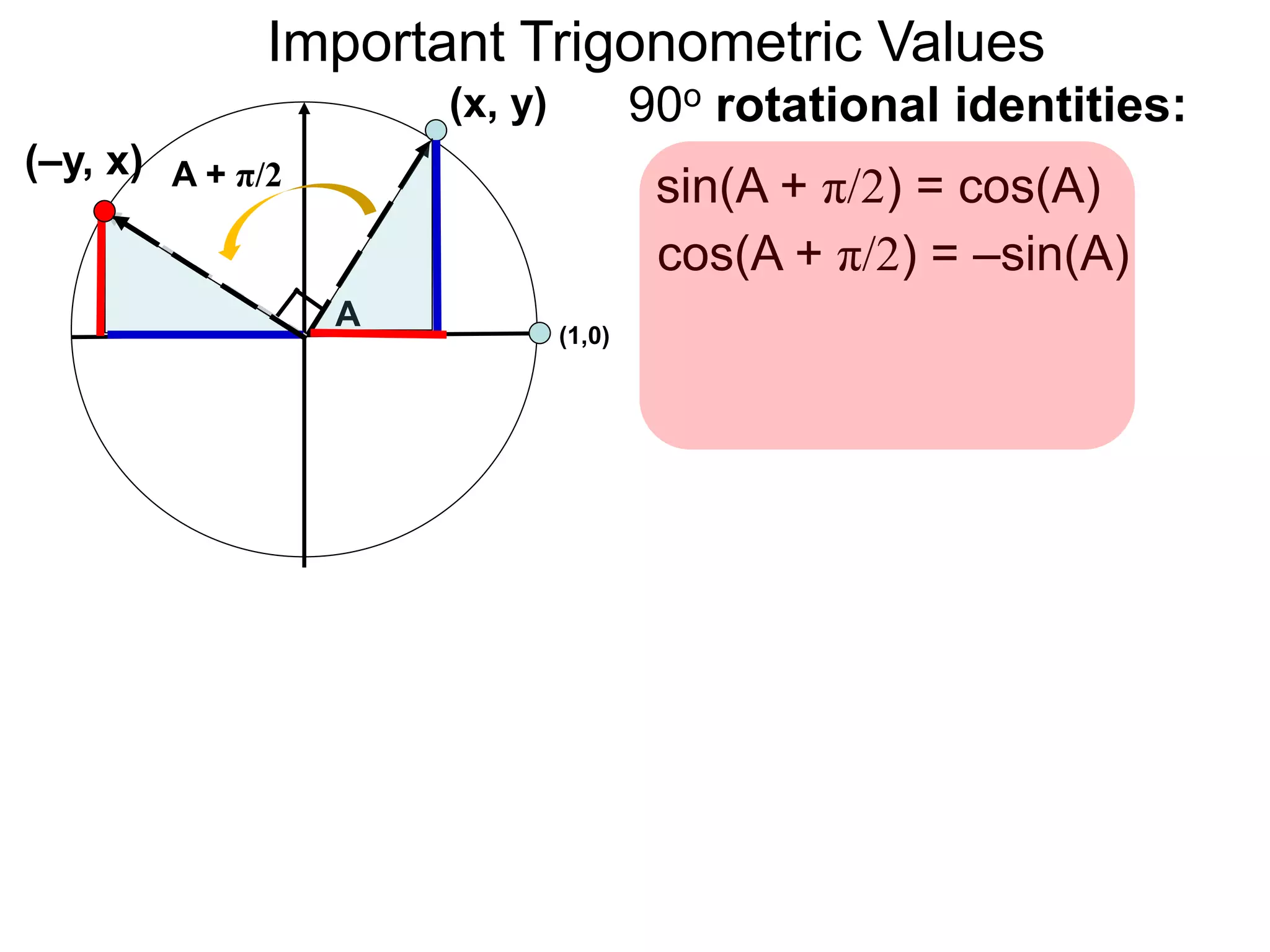
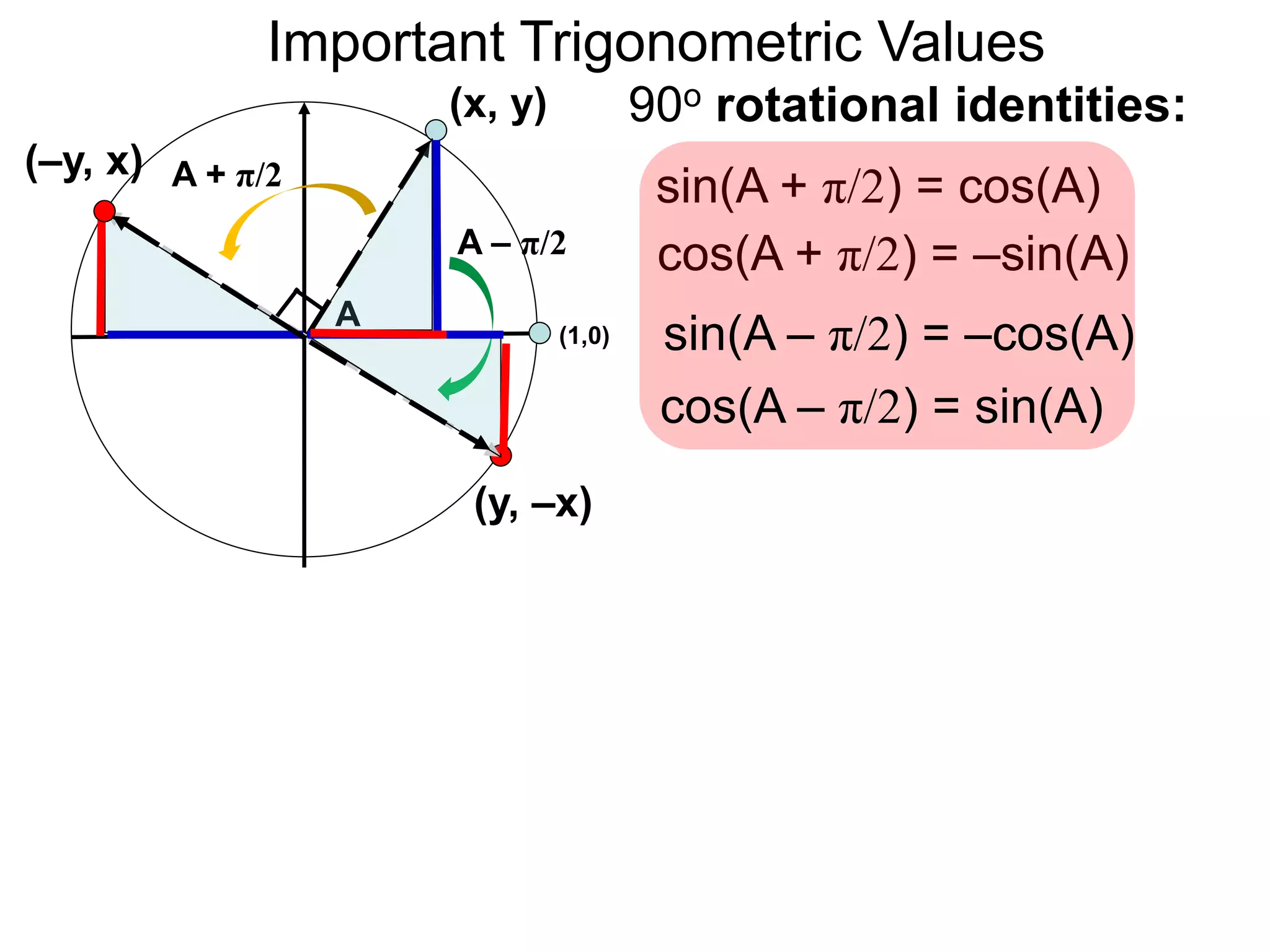
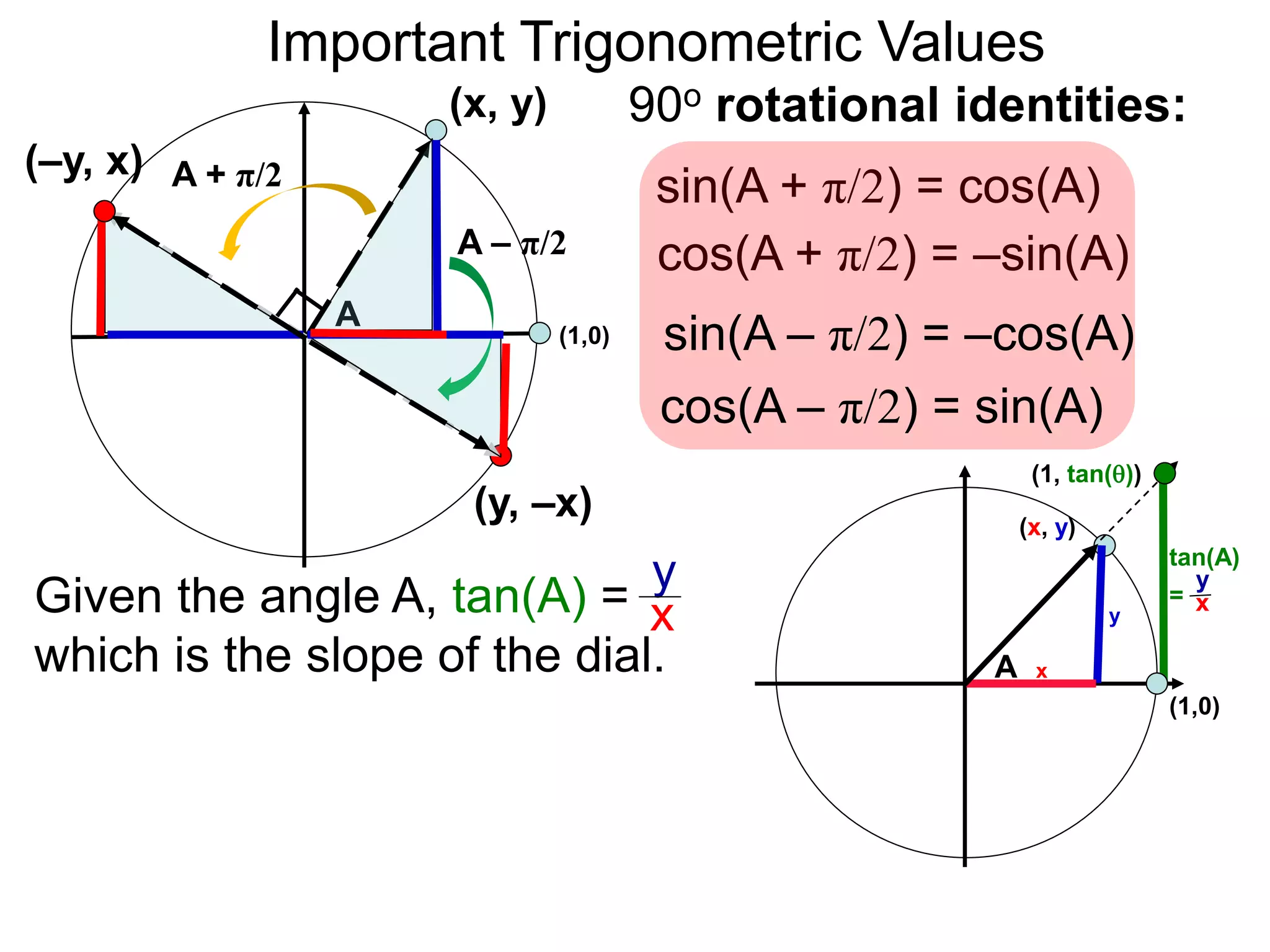
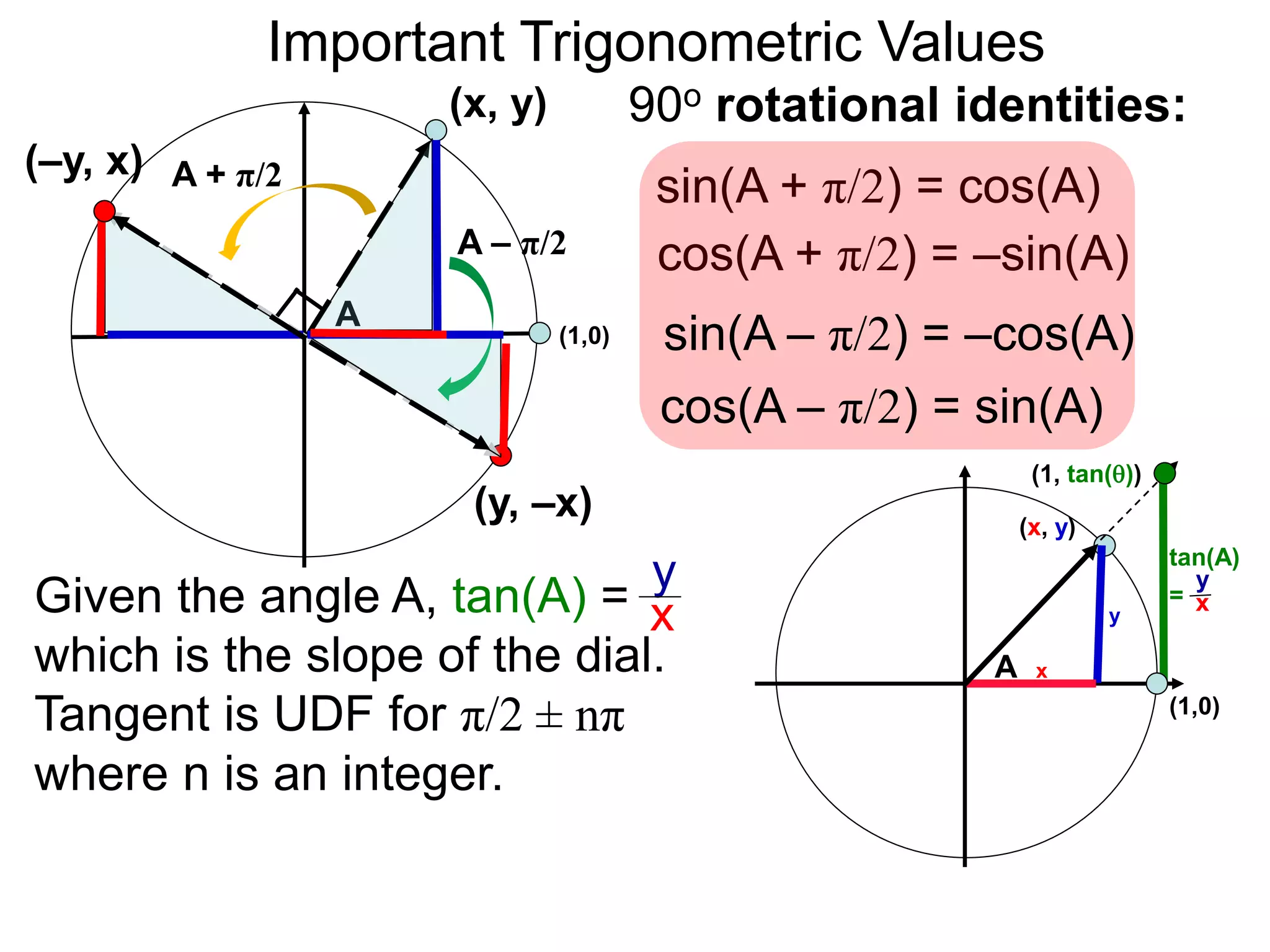
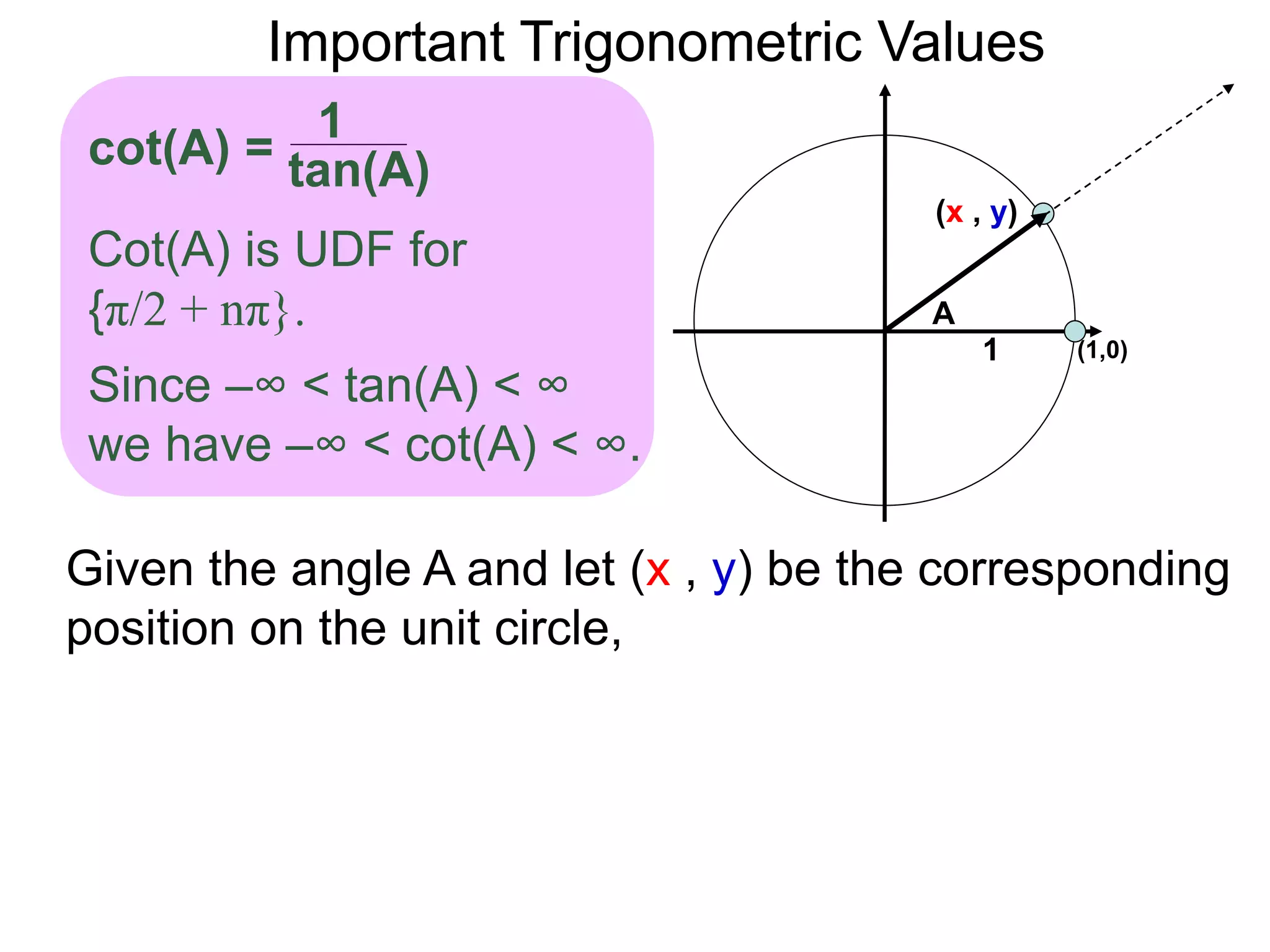
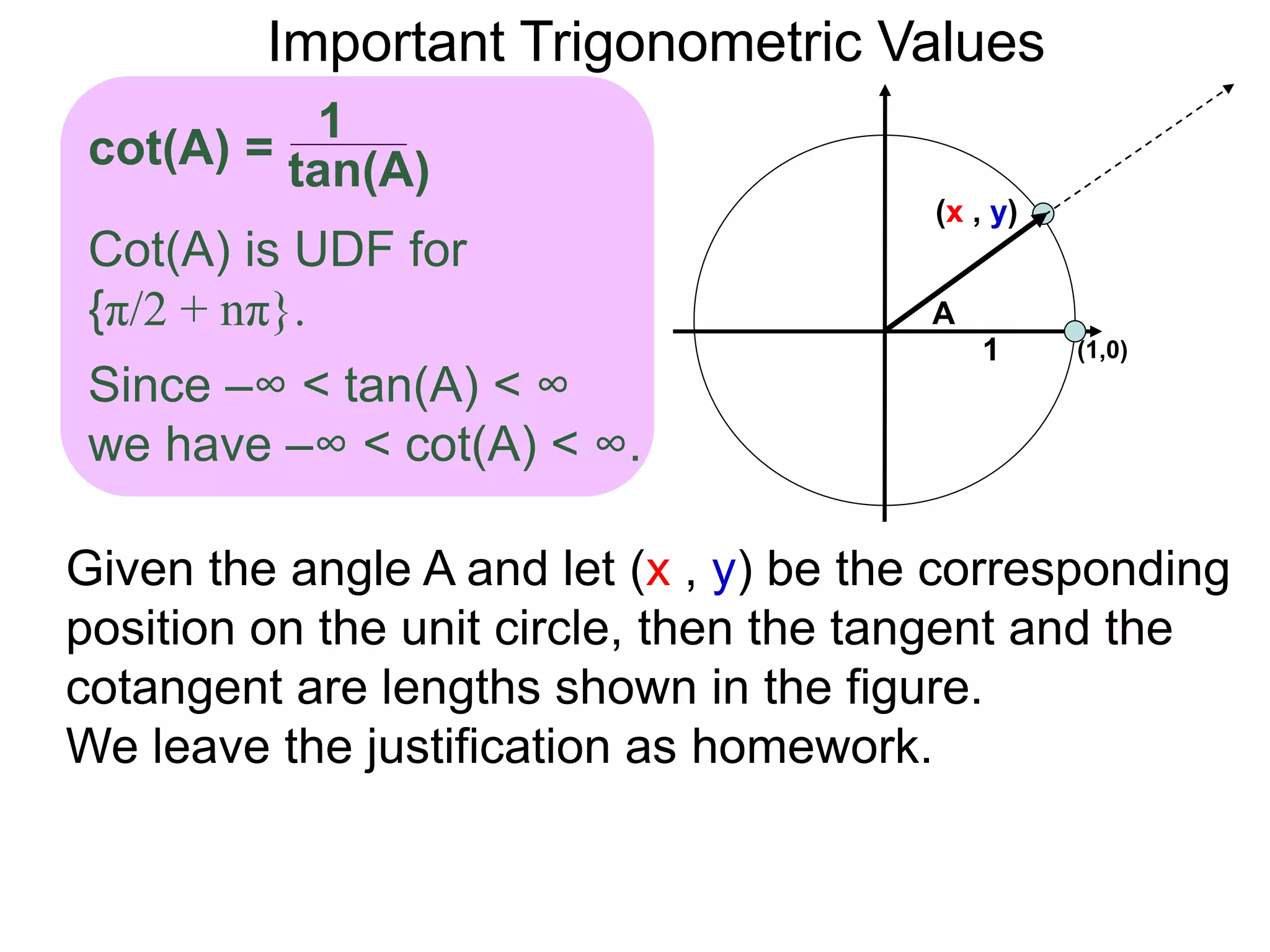
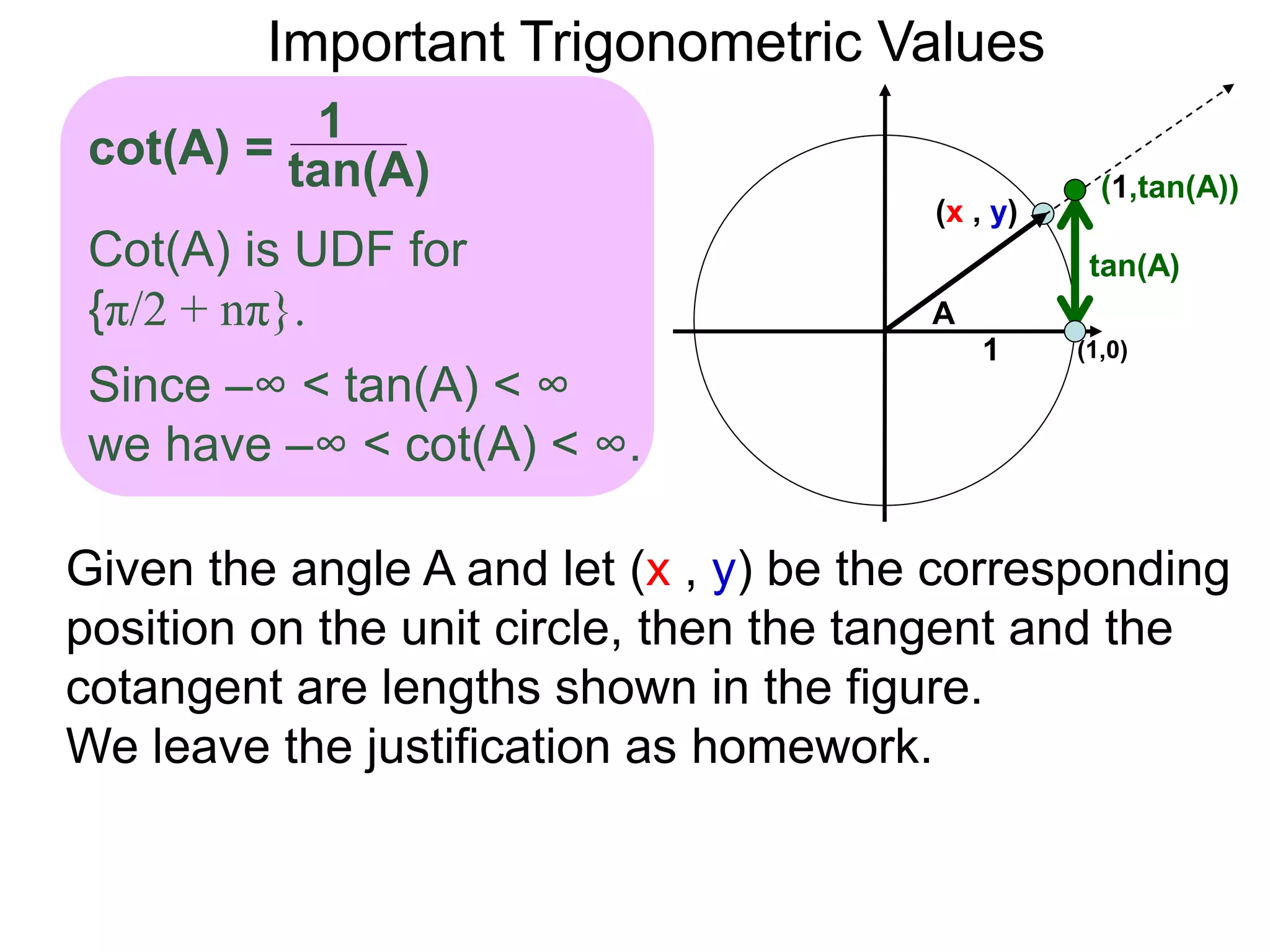
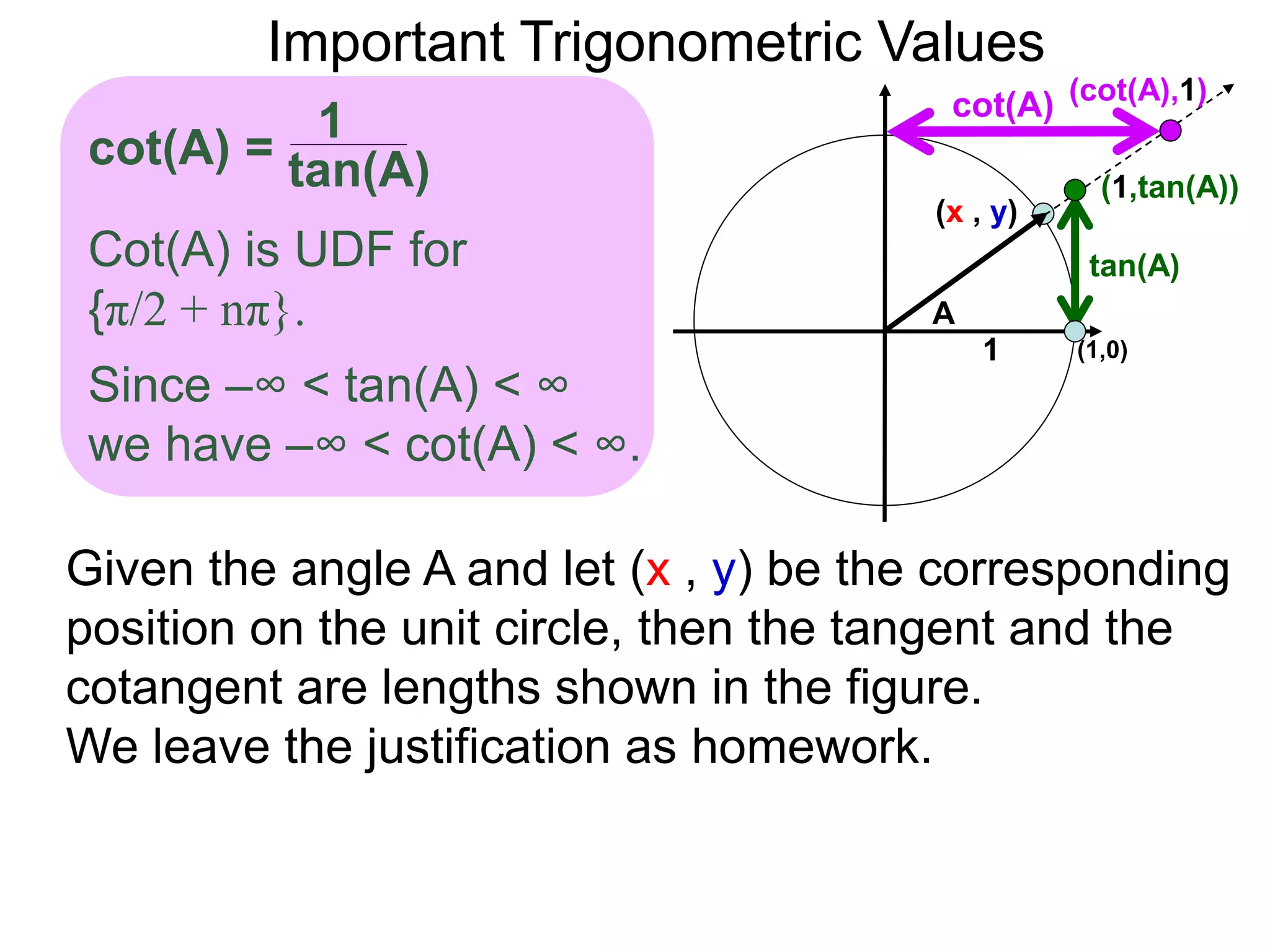
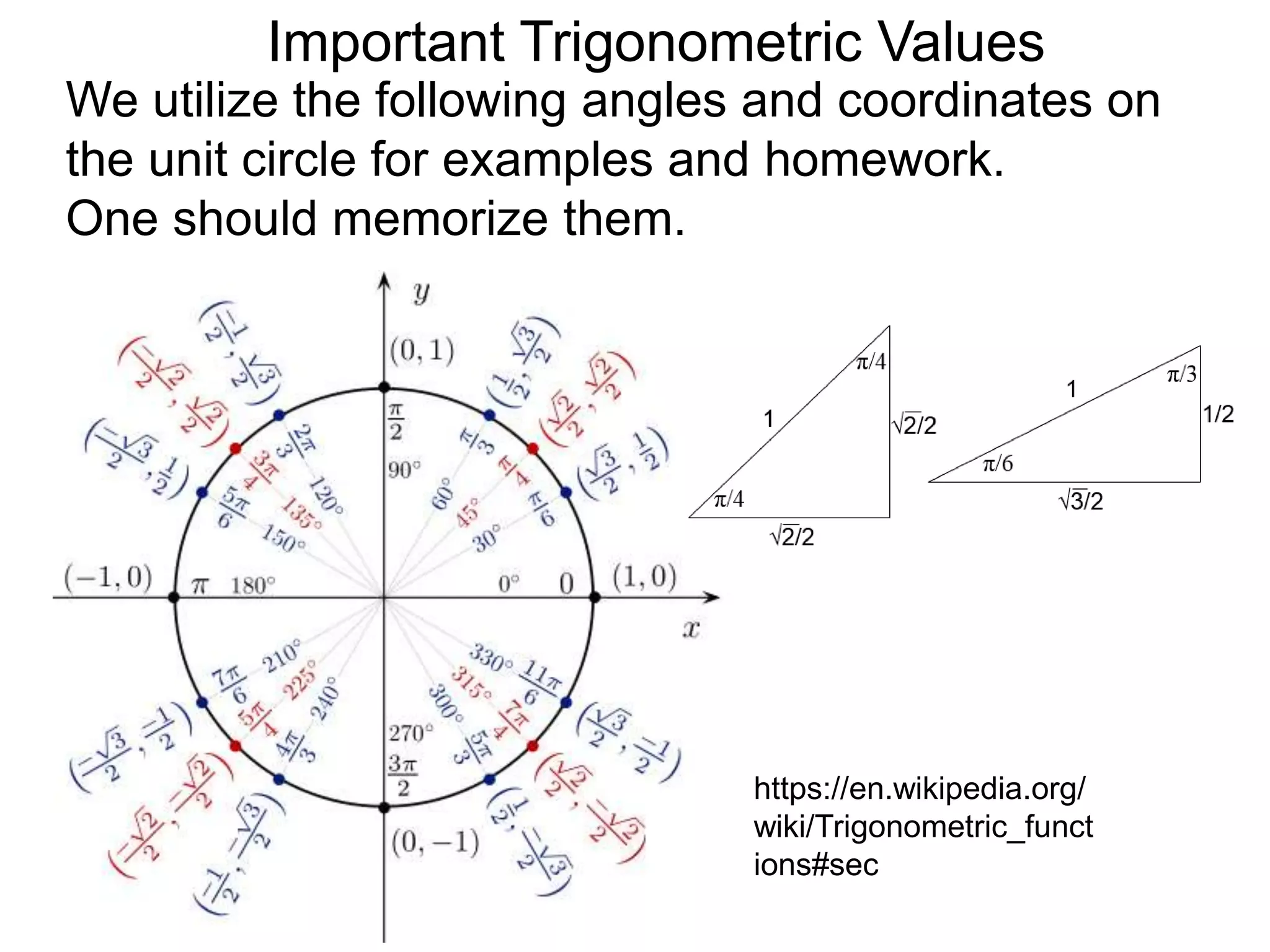
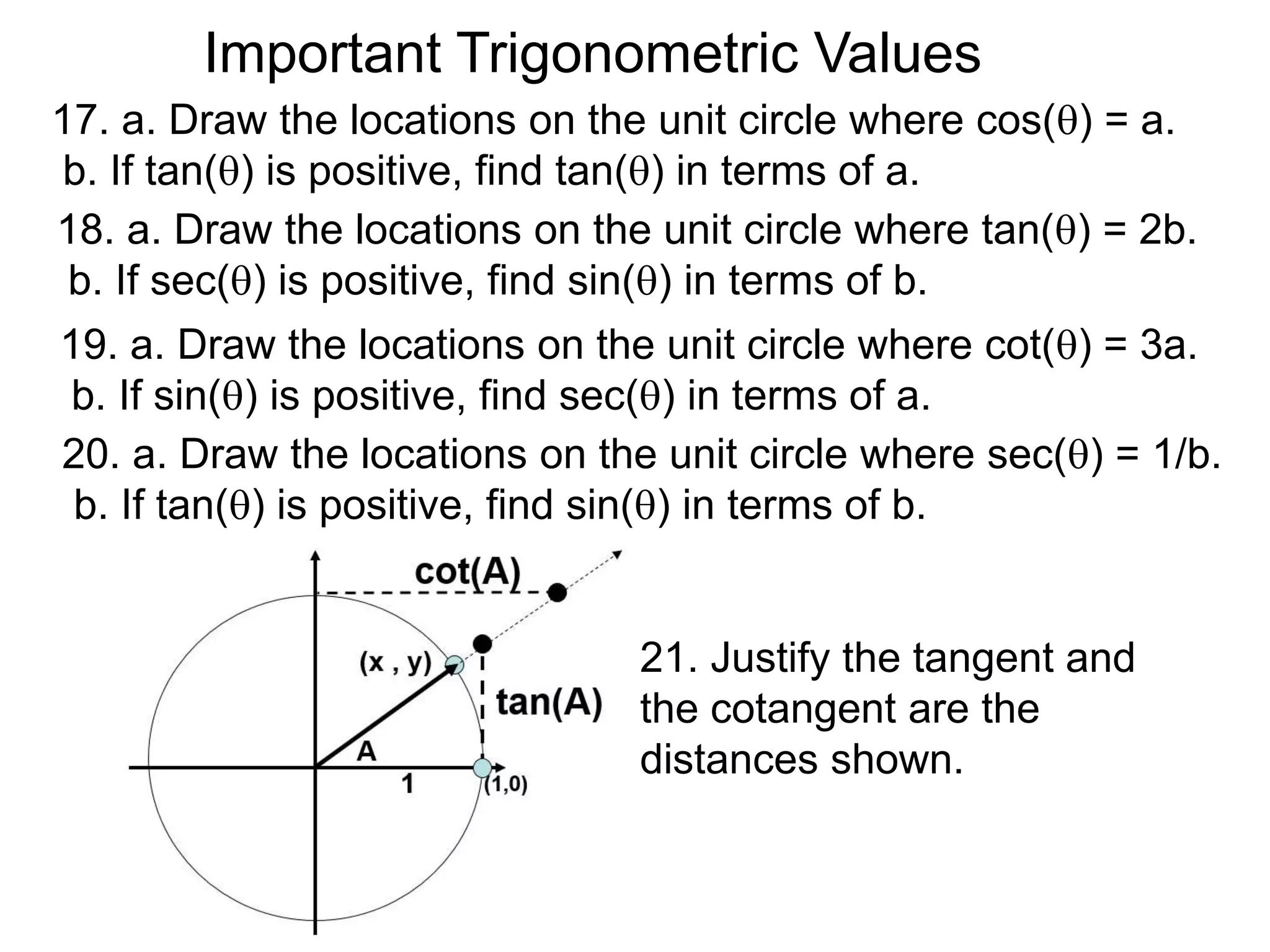
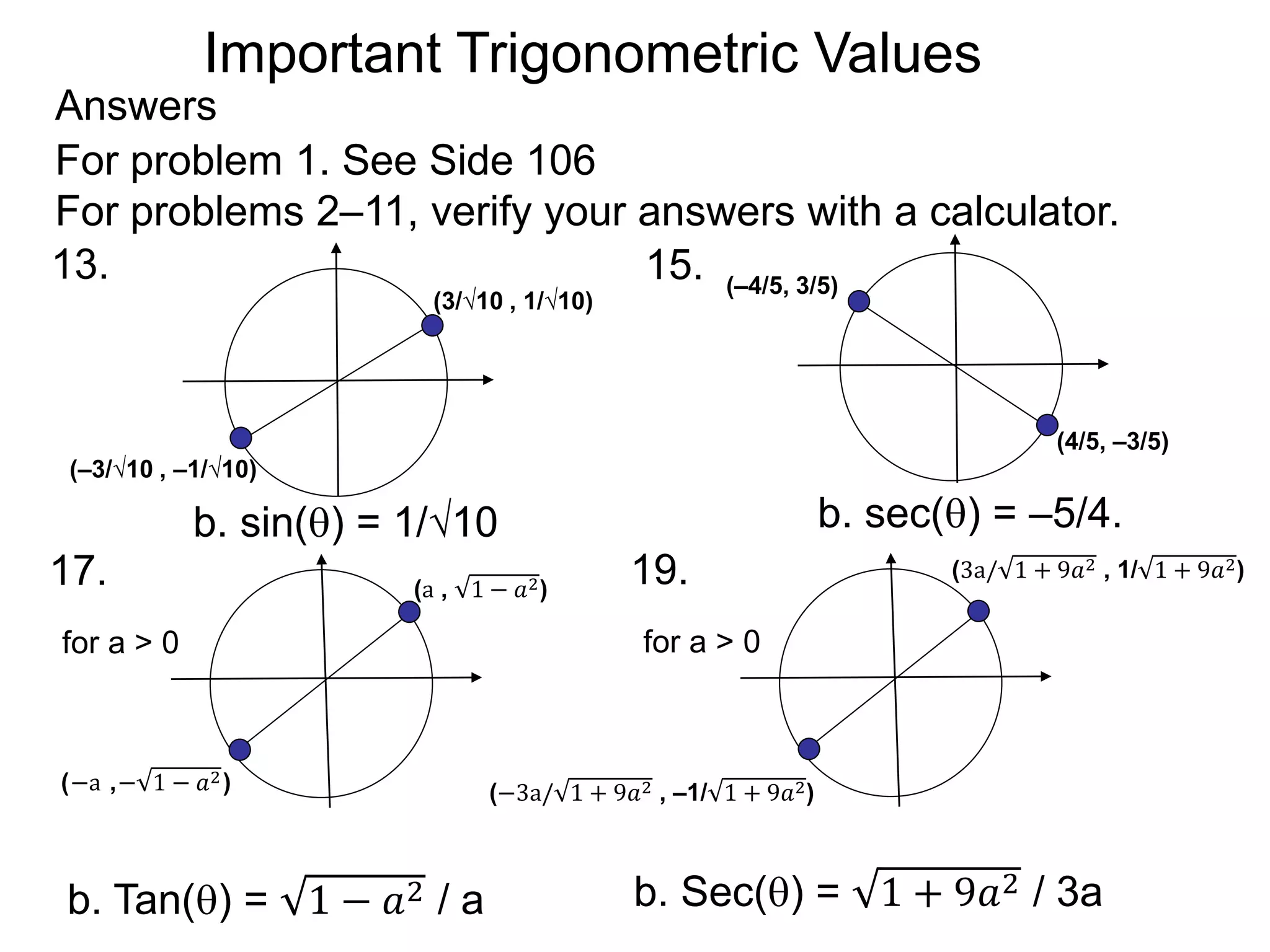
The document discusses radian measurements of angles using the unit circle. It defines the unit circle as having a radius of 1 centered at the origin. The radian measurement of an angle is defined as the length of the arc cut out by that angle on the unit circle. Important conversions between degrees and radians are provided. Trigonometric functions like sine, cosine, and tangent are then defined using the unit circle for any real number angle measurement.

1. Radian Measurements
The unit circle is the circle
centered at (0, 0) with radius 1.

2. Radian Measurements
r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
(1, 0)

3. Radian Measurements
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of the equation
x2 + y2 = 1.
r = 1
(1, 0)

4. The radian measurement of an
angle is the length of the arc
that the angle cuts out on the
unit circle.
Radian Measurements
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of the equation
x2 + y2 = 1.
r = 1
(1, 0)

5. The radian measurement of an
angle is the length of the arc
that the angle cuts out on the
unit circle.
Arc length as angle
measurement for 
Radian Measurements

r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of the equation
x2 + y2 = 1.
(1, 0)

6. The radian measurement of an
angle is the length of the arc
that the angle cuts out on the
unit circle.
Arc length as angle
measurement for 
Radian Measurements

Hence 2π rad, the circumference of the unit circle,
is the radian measurement for the 360o angle.
r = 1
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of the equation
x2 + y2 = 1.
(1, 0)

7. The radian measurement of an
angle is the length of the arc
that the angle cuts out on the
unit circle.
Arc length as angle
measurement for 
Radian Measurements

Hence 2π rad, the circumference of the unit circle,
is the radian measurement for the 360o angle.
r = 1
Important Conversions between Degree and Radian
π
180 π
180o
The unit circle is the circle
centered at (0, 0) with radius 1.
It's the graph of the equation
x2 + y2 = 1.
1o =  0.0175 rad 1 rad =  57o
180o = π rad 90o = radπ
2 60o = radπ
3 45o = radπ
4
(1, 0)

8. Let’s extend the measurements
of angles to all real numbers.
Trigonometric Functions via the Unit Circle

9. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
Trigonometric Functions via the Unit Circle

10. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise,
 is +
Trigonometric Functions via the Unit Circle

11. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.
 is +
 is –
Trigonometric Functions via the Unit Circle

12. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.
(1,0)

 is +
 is –
(x , y)
Trigonometric Functions via the Unit Circle
Given  in the standard position,
let the coordinate of the tip of the
dial on the unit circle be (x, y),

13. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.
(1,0)

 is +
 is –
y=sin()
(x , y)
Trigonometric Functions via the Unit Circle
Given  in the standard position,
let the coordinate of the tip of the
dial on the unit circle be (x, y),
we define:
sin() = y,

14. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.
(1,0)

x=cos()
 is +
 is –
y=sin()
(x , y)
Trigonometric Functions via the Unit Circle
Given  in the standard position,
let the coordinate of the tip of the
dial on the unit circle be (x, y),
we define:
sin() = y, cos() = x,

15. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.
(1,0)

x=cos()
 is +
 is –
y=sin()
(x , y)
tan()
Trigonometric Functions via the Unit Circle
Given  in the standard position,
let the coordinate of the tip of the
dial on the unit circle be (x, y),
we define:
sin() = y, cos() = x, tan() = y
x
(1, tan())

16. Let’s extend the measurements
of angles to all real numbers. We
say an angle  is in the standard
position if it’s formed by spinning
a dial against the positive x–axis.
The direction of the spin sets the
sign of ,  is set to positive if it’s
formed counter-clockwise, and
negative if it’s formed clockwise.(1, tan())
Given  in the standard position,
let the coordinate of the tip of the
dial on the unit circle be (x, y),
we define:
sin() = y, cos() = x, tan() =

x=cos()
 is +
 is –
y=sin()
(x , y)
y
x
tan()
Note: The slope of the dial is tan().
Trigonometric Functions via the Unit Circle
(1,0)

17. Important Trigonometric Values
From here on, all angles measurements will be in
radian, unless stated otherwise.

18. Angles with measurements of nπ rad,
where n = 0,1,2,3.. .is an integer,
correspond to the x–axial angles.
0, ±2π, ±4π..±π, ±3π..
Important Trigonometric Values
From here on, all angles measurements will be in
radian, unless stated otherwise.

19. Angles with measurements of nπ rad,
where n = 0,1,2,3.. .is an integer,
correspond to the x–axial angles.
0, ±2π, ±4π..±π, ±3π..
Angles with measurements of
rad correspond
to the y–axial angles.
.. –3π/2, π/2, 5π/2..
..–5π/2, –π/2, 3π/2 , 7π/2..
kπ
2
Important Trigonometric Values
From here on, all angles measurements will be in
radian, unless stated otherwise.

20. Angles with measurements of nπ rad,
where n = 0,1,2,3.. .is an integer,
correspond to the x–axial angles.
0, ±2π, ±4π..±π, ±3π..
Angles with measurements of
rad correspond
to the y–axial angles.
.. –3π/2, π/2, 5π/2..
..–5π/2, –π/2, 3π/2 , 7π/2..
Angles with measurements of
rad are diagonals.
π/4, –7π/4..3π/4, –5π/4..
5π/4, –3π/4.. 7π/4, –π/4..
kπ
2
4
kπ
Important Trigonometric Values
From here on, all angles measurements will be in
radian, unless stated otherwise.

21. Angles with measurements of nπ rad,
where n = 0,1,2,3.. .is an integer,
correspond to the x–axial angles.
0, ±2π, ±4π..±π, ±3π..
Angles with measurements of
rad correspond
to the y–axial angles.
.. –3π/2, π/2, 5π/2..
..–5π/2, –π/2, 3π/2 , 7π/2..
Angles with measurements of
rad are diagonals.
π/4, –7π/4..3π/4, –5π/4..
5π/4, –3π/4.. 7π/4, –π/4..
Angles with measurements of
(reduced) or rad. π/6, –11π/6..
π/3, –5π/3..2π/3,..
5π/6,..
7π/6,..
4π/3,.. 5π/3,..
11π/6,..
kπ
2
4
6 3
kπ
kπ k π
Important Trigonometric Values
These are the clock hourly positions.
From here on, all angles measurements will be in
radian, unless stated otherwise.

22. Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle .

23. Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,

24. Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,
so the dial spin to the same position for  and  + 2nπ
and  and  + 2nπ have the same trig-outputs.

25. Two Important Right Triangles
Recall the following two triangles which are useful for
extracting the trigonometric values of angles related
to π/4, π/6 and π/3.
Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,
so the dial spin to the same position for  and  + 2nπ
and  and  + 2nπ have the same trig-outputs.

26. Two Important Right Triangles
Recall the following two triangles which are useful for
extracting the trigonometric values of angles related
to π/4, π/6 and π/3. From these “templates” we can
determine the trig-values of the following angles.
Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,
so the dial spin to the same position for  and  + 2nπ
and  and  + 2nπ have the same trig-outputs.

27. Two Important Right Triangles
Recall the following two triangles which are useful for
extracting the trigonometric values of angles related
to π/4, π/6 and π/3. From these “templates” we can
determine the trig-values of the following angles.
Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,
so the dial spin to the same position for  and  + 2nπ
and  and  + 2nπ have the same trig-outputs.
I. (nπ/4) : The angles at the
diagonal positions (n is odd.)

28. Two Important Right Triangles
Recall the following two triangles which are useful for
extracting the trigonometric values of angles related
to π/4, π/6 and π/3. From these “templates” we can
determine the trig-values of the following angles.
Important Trigonometric Values
The trig–values of an angle  depend on the position
of the dial at the angle . For an integer n, the angle
2nπ corresponds to spinning n complete cycles,
so the dial spin to the same position for  and  + 2nπ
and  and  + 2nπ have the same trig-outputs.
I. (nπ/4) : The angles at the
diagonal positions (n is odd.)
II. (nπ/6) : The angles at the
clock hourly positions.

29. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
Important Trigonometric Values

30. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
Important Trigonometric Values

31. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Important Trigonometric Values

32. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Important Trigonometric Values

33. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Important Trigonometric Values
5π/4

34. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Place the π/4–rt–triangle as shown,
Important Trigonometric Values
5π/4

35. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Place the π/4–rt–triangle as shown,
1
Important Trigonometric Values
5π/4

36. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
5π/4
(–2/2, –2/2)
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
Place the π/4–rt–triangle as shown,
we get the coordinate = (–2/2, –2/2).
1
Important Trigonometric Values

37. Example A. Draw the angle, label the coordinates of
the corresponding position on the unit circle and list
the sine, cosine, and tangent trig–values.
a.  = –3π
(–2/2, –2/2)
–3π
(–1, 0)
b.  = 5π/4
sin(–3π) = 0
cos(–3π) = –1
tan(–3π) = 0
sin(5π/4) = –2/2
tan(5π/4) = 1
cos(5π/4) = –2/2
Place the π/4–rt–triangle as shown,
we get the coordinate = (–2/2, –2/2).
1
Important Trigonometric Values
5π/4

38. c.  = –11π/6
Important Trigonometric Values

39. c.  = –11π/6
–11π/6
1
Important Trigonometric Values

40. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2). 1
Important Trigonometric Values

41. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2).
sin(–11π/6) = 1/2
cos(–11π/6) = 3/2
tan(–11π/6) = 1/3 =3/3
1
Important Trigonometric Values

42. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2).
sin(–11π/6) = 1/2
cos(–11π/6) = 3/2
tan(–11π/6) = 1/3 =3/3
1
Important Trigonometric Values
Conversely, in general, there are two locations on the
unit circle having a specified trig-value.

43. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2).
sin(–11π/6) = 1/2
cos(–11π/6) = 3/2
tan(–11π/6) = 1/3 =3/3
1
Important Trigonometric Values
Example B. a. Find the two locations on
the unit circle where tan() = 3/4. Draw.
Conversely, in general, there are two locations on the
unit circle having a specified trig-value.

44. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2).
sin(–11π/6) = 1/2
cos(–11π/6) = 3/2
tan(–11π/6) = 1/3 =3/3
1
Important Trigonometric Values
Example B. a. Find the two locations on
the unit circle where tan() = 3/4. Draw.
We want the points (x, y) on the circle
where tan() = y/x = ¾.
(x, y)
Conversely, in general, there are two locations on the
unit circle having a specified trig-value.

45. c.  = –11π/6
–11π/6
(3/2, ½)
Place the π/6–rt–triangle as shown,
we get the coordinate = (3/2, 1/2).
sin(–11π/6) = 1/2
cos(–11π/6) = 3/2
tan(–11π/6) = 1/3 =3/3
1
Important Trigonometric Values
Example B. a. Find the two locations on
the unit circle where tan() = 3/4. Draw.
We want the points (x, y) on the circle
where tan() = y/x = ¾.
Here are two ways to obtain the answers.
(x, y)
Conversely, in general, there are two locations on the
unit circle having a specified trig-value.

46. Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,

47. Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.

48. Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,

49. Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).

50. Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).
(4, 3)
(x, y) = (4/5, 3/5)
(–4/5, –3/5)

51. Il. (Using proportional triangles)
Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).
Given that
(4, 3)
y
=x 4
3 we have that (4, 3) is a point
on the radial line through (x, y).
(x, y) = (4/5, 3/5)
(–4/5, –3/5)

52. Il. (Using proportional triangles)
Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).
Given that
(4, 3)
y
=x 4
3 we have that (4, 3) is a point
on the radial line through (x, y).
The point (4, 3) is 5 units away
from the origin (why?).
(x, y) = (4/5, 3/5)
(–4/5, –3/5)

53. Il. (Using proportional triangles)
Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).
Given that
(4, 3)
y
=x 4
3 we have that (4, 3) is a point
on the radial line through (x, y).
The point (4, 3) is 5 units away
from the origin (why?).
By dividing the coordinates by 5,
so (x, y) = (4/5, 3/5) and the
other point is (–4/5, –3/5).
(x, y) = (4/5, 3/5)
(–4/5, –3/5)

54. Il. (Using proportional triangles)
Important Trigonometric Values
I. (Numerical Computation) We’ve y/x = ¾ or y = ¾ x,
so by the Pythagorean Theorem, x2 + (¾ x)2 = 1.
Solving for x, we get x2 = 16/25 or x = ±4/5,
so (x, y) = (4/5, 3/5) or (–4/5, –3/5).
Given that
(4, 3)
y
=x 4
3 we have that (4, 3) is a point
on the radial line through (x, y).
The point (4, 3) is 5 units away
from the origin (why?).
By dividing the coordinates by 5,
so (x, y) = (4/5, 3/5) and the
other point is (–4/5, –3/5).
(x, y) = (4/5, 3/5)
(–4/5, –3/5)
Buy providing more information
we may narrow the answer to one location.

55. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.

56. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).

57. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5). (–4/5, –3/5)

58. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)

59. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.

60. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
1/3

61. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
Sin() = 1/3 = y, so x2 + (1/3)2 = 1
1/3

62. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
Sin() = 1/3 = y, so x2 + (1/3)2 = 1
and that x = ±√8/9 = ±(2√2)/3. 1/3

63. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
Sin() = 1/3 = y, so x2 + (1/3)2 = 1
and that x = ±√8/9 = ±(2√2)/3.
Both points are at the top-half of
the circle as shown.
(–(2√2)/3, 1/3) ((2√2)/3, 1/3)
1/3

64. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
Sin() = 1/3 = y, so x2 + (1/3)2 = 1
and that x = ±√8/9 = ±(2√2)/3.
Both points are at the top-half of
the circle as shown.
b. What is cos() if tan() is negative?
1/3
(–(2√2)/3, 1/3) ((2√2)/3, 1/3)

65. Important Trigonometric Values
Example B. b. Find cos()
if tan() = ¾ and that sin() is negative.
The two points where tan() = ¾
are (4/5, 3/5) or (–4/5, –3/5).
The one with negative sin() or y
must is (–4/5, –3/5), hence cos() = –4/5.
(–4/5, –3/5)
Example C. a. Draw and find the locations on
the unit circle where sin() = 1/3.
Sin() = 1/3 = y, so x2 + (1/3)2 = 1
and that x = ±√8/9 = ±(2√2)/3.
Both points are at the top-half of
the circle as shown.
b. What is cos() if tan() is negative?
If tan() is negative, we have cos() = –(2√2)/3.
1/3
(–(2√2)/3, 1/3) ((2√2)/3, 1/3)

66. Important Trigonometric Values
Here are some basic facts of sine, cosine and tangent
as the consequences of the unit–circle definition.

67. Important Trigonometric Values
Here are some basic facts of sine, cosine and tangent
as the consequences of the unit–circle definition.
For all angles A:
* –1 ≤ sin(A) ≤ 1
or l sin(A) l ≤ 1
(1,0)
A
sin(A)
(x , y)

68. Important Trigonometric Values
Here are some basic facts of sine, cosine and tangent
as the consequences of the unit–circle definition.
For all angles A:
* –1 ≤ sin(A) ≤ 1
or l sin(A) l ≤ 1
* sin(–A) = –sin(A)
(1,0)
A
sin(A)
(x , y)
–A
sin(–A)
(x , –y)

69. Important Trigonometric Values
Here are some basic facts of sine, cosine and tangent
as the consequences of the unit–circle definition.
For all angles A:
* –1 ≤ sin(A) ≤ 1
or l sin(A) l ≤ 1
* sin(–A) = –sin(A)
(1,0)
A
sin(A)
(x , y)
–A
sin(–A)
(1,0)
A
cos(A)
(x , y)
(x , –y)
* –1 ≤ cos(A) ≤ 1
or l cos(A) l ≤ 1

70. Important Trigonometric Values
Here are some basic facts of sine, cosine and tangent
as the consequences of the unit–circle definition.
For all angles A:
* –1 ≤ sin(A) ≤ 1
or l sin(A) l ≤ 1
* sin(–A) = –sin(A)
(1,0)
A
sin(A)
(x , y)
–A
sin(–A)
(1,0)
A
cos(A) = cos(–A)
(x , y)
–A
(x , –y) (x , –y)
* –1 ≤ cos(A) ≤ 1
or l cos(A) l ≤ 1
* cos(–A) = cos(A)

71. Important Trigonometric Values
Rotational Identities

72. Important Trigonometric Values
Rotational Identities
Given an angle A and let (x, y) be the point on the
unit circle corresponding to A,
A
(x , y)
(1,0)

73. Important Trigonometric Values
Rotational Identities
Given an angle A and let (x, y) be the point on the
unit circle corresponding to A, since the angles
(A + π) and (A – π) point in the opposite direction of A
A
(x , y)
(1,0)
A – π
A + π

74. Important Trigonometric Values
Rotational Identities
Given an angle A and let (x, y) be the point on the
unit circle corresponding to A, since the angles
(A + π) and (A – π) point in the opposite direction of A
so (–x, –y) corresponds to (A + π) and (A – π).
A
(x , y)
(–x , –y)
(1,0)
A – π
A + π

75. Important Trigonometric Values
Rotational Identities
Given an angle A and let (x, y) be the point on the
unit circle corresponding to A, since the angles
(A + π) and (A – π) point in the opposite direction of A
so (–x, –y) corresponds to (A + π) and (A – π).
A
(x , y)
(–x , –y)
sin(A ± π) = –sin(A)
cos(A ± π) = –cos(A)
180o rotational identities:
(1,0)
A – π
A + π

76. Important Trigonometric Values
Rotational Identities
Given an angle A and let (x, y) be the point on the
unit circle corresponding to A, since the angles
(A + π) and (A – π) point in the opposite direction of A
so (–x, –y) corresponds to (A + π) and (A – π).
(1,0)A
(x , y)
A – π
(–x , –y)
sin(A ± π) = –sin(A)
cos(A ± π) = –cos(A)
(A + π/2 ) and (A – π/2) are 90o
counterclockwise and clockwise
rotations of A and the points
(–y, x) and (y, –x) correspond to
A + π/2 and A – π/2 respectively.
180o rotational identities:
(–y, x)
(y, –x)
A + π

77. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2(–y, x)
90o rotational identities:

78. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2(–y, x)
sin(A + π/2) = cos(A)
90o rotational identities:

79. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:

80. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2
A – π/2
(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:
(y, –x)
sin(A – π/2) = –cos(A)
cos(A – π/2) = sin(A)

81. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2
A – π/2
(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:
(y, –x)
sin(A – π/2) = –cos(A)
cos(A – π/2) = sin(A)
(1,0)
A x
y
(x, y)
Given the angle A, tan(A) =
y
x

82. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2
A – π/2
(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:
(y, –x)
sin(A – π/2) = –cos(A)
cos(A – π/2) = sin(A)
(1,0)
A x
y
(x, y)
tan(A)
=Given the angle A, tan(A) =
which is the slope of the dial.
y
x
y
x
(1, tan())

83. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2
A – π/2
(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:
(y, –x)
sin(A – π/2) = –cos(A)
cos(A – π/2) = sin(A)
(1,0)
A x
y
(x, y)
tan(A)
=Given the angle A, tan(A) =
which is the slope of the dial.
Tangent is UDF for π/2 ± nπ
where n is an integer.
y
x
y
x
(1, tan())

84. Important Trigonometric Values
(1,0)
A
(x, y)
A + π/2
A – π/2
(–y, x)
sin(A + π/2) = cos(A)
cos(A + π/2) = –sin(A)
90o rotational identities:
(y, –x)
sin(A – π/2) = –cos(A)
cos(A – π/2) = sin(A)
(1,0)
A x
y
(x, y)
tan(A)
=Given the angle A, tan(A) =
which is the slope of the dial.
Tangent is UDF for π/2 ± nπ
where n is an integer. In particular
y
x
y
x
–∞ < tan(A) < ∞
tan(A ± π) = tan(A) tan(A ± π/2) = –1/tan(A)
(1, tan())

85. Important Trigonometric Values
Given an angle A, its horizontal reflection is (π – A).
From that we have:
sin(A) = sin(π – A)
(1,0)
A
(x , y)
π – A
(–x , y)
cos(A) = –cos(π – A)
tan(A) = –tan(π – A)

86. Important Trigonometric Values
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.

87. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.

88. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.

89. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.
Since l cos(A) l ≤ 1
we’ve I sec(A) l ≥ 1.

90. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.
Since l cos(A) l ≤ 1
we’ve I sec(A) l ≥ 1.
Specifically,
sec(A) ≥ 1 for 0 ≤ A < π/2,
sec(A) ≤ –1 for π/2 < A ≤ π.

91. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.
Since l cos(A) l ≤ 1
we’ve I sec(A) l ≥ 1.
Specifically,
sec(A) ≥ 1 for 0 ≤ A < π/2,
sec(A) ≤ –1 for π/2 < A ≤ π.
sin(A)
1
csc(A) =

92. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.
Since l cos(A) l ≤ 1
we’ve I sec(A) l ≥ 1.
Specifically,
sec(A) ≥ 1 for 0 ≤ A < π/2,
sec(A) ≤ –1 for π/2 < A ≤ π.
sin(A)
1
csc(A) =
Cosecant is UDF for
{nπ} with integer n.

93. Important Trigonometric Values
cos(A)
1
sec(A) =
The reciprocals of sine, cosine, and tangent
appear frequently amongst their algebraic relations.
Hence we define secant, cosecant, and cotangent
as their reciprocals respectively.
Secant is UDF for
{π/2 + nπ} with integer n.
Since l cos(A) l ≤ 1
we’ve I sec(A) l ≥ 1.
Specifically,
sec(A) ≥ 1 for 0 ≤ A < π/2,
sec(A) ≤ –1 for π/2 < A ≤ π.
sin(A)
1
csc(A) =
Cosecant is UDF for
{nπ} with integer n.
Since l sin(A) l ≤ 1 we
have I csc(A) l ≥ 1.
Specifically,
csc(A) ≥ 1 for 0 < A ≤ π/2,
csc(A) ≤ –1 for –π/2 <A ≤ 0.

94. Important Trigonometric Values
tan(A)
1
cot(A) =

95. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
tan(A)
1
cot(A) =

96. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
Since –∞ < tan(A) < ∞
we have –∞ < cot(A) < ∞.
tan(A)
1
cot(A) =

97. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
Since –∞ < tan(A) < ∞
we have –∞ < cot(A) < ∞.
tan(A)
1
cot(A) =
Given the angle A and let (x , y) be the corresponding
position on the unit circle,
(1,0)
(x , y)
A
1

98. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
Since –∞ < tan(A) < ∞
we have –∞ < cot(A) < ∞.
tan(A)
1
cot(A) =
(1,0)
(x , y)
Given the angle A and let (x , y) be the corresponding
position on the unit circle, then the tangent and the
cotangent are lengths shown in the figure.
We leave the justification as homework.
A
1

99. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
Since –∞ < tan(A) < ∞
we have –∞ < cot(A) < ∞.
tan(A)
1
cot(A) =
(1,0)
(x , y)
tan(A)
Given the angle A and let (x , y) be the corresponding
position on the unit circle, then the tangent and the
cotangent are lengths shown in the figure.
We leave the justification as homework.
(1,tan(A))
A
1

100. Important Trigonometric Values
Cot(A) is UDF for
{π/2 + nπ}.
Since –∞ < tan(A) < ∞
we have –∞ < cot(A) < ∞.
tan(A)
1
cot(A) =
(1,0)
A
(x , y)
tan(A)
Given the angle A and let (x , y) be the corresponding
position on the unit circle, then the tangent and the
cotangent are lengths shown in the figure.
We leave the justification as homework.
cot(A)
1
(1,tan(A))
(cot(A),1)

101. Important Trigonometric Values
With the unit–circle definition, except at isolated
inputs, the trig-functions are defined for all angles,
thus removing the restriction of the SOCAHTOA
definition based on right triangles.

102. Important Trigonometric Values
With the unit–circle definition, except at isolated
inputs, the trig-functions are defined for all angles,
thus removing the restriction of the SOCAHTOA
definition based on right triangles.
Since trig–functions produce the same output for
every 2nπ increment, i.e. for any trig–function f,
f(x) = f(x + 2nπ), where n is an integer,
trig–functions are useful to describe cyclical data.
Circadian Rhythms
Circadian rhythms are the bio–rhythms of a person
or of any living beings, that fluctuate through out
some fixed period of time: hourly, daily, etc..
For people, the measurements could be the blood
pressures, or the heart rates, etc..

103. Important Trigonometric Values
With the unit–circle definition, except at isolated
inputs, the trig-functions are defined for all angles,
thus removing the restriction of the SOCAHTOA
definition based on right triangles.
Since trig–functions produce the same output for
every 2nπ increment, i.e. for any trig–function f,
f(x) = f(x + 2nπ), where n is an integer,
trig–functions are useful to describe cyclical data.
Circadian Rhythms
Circadian rhythms are the bio–rhythms of a person
or of any living beings, that fluctuate through out
some fixed period of time: hourly, daily, etc..
For people, the measurements could be the blood
pressures, or the heart rates, etc..

104. Important Trigonometric Values
With the unit–circle definition, except at isolated
inputs, the trig-functions are defined for all angles,
thus removing the restriction of the SOCAHTOA
definition based on right triangles.
Since trig–functions produce the same output for
every 2nπ increment, i.e. for any trig–function f,
f(x) = f(x + 2nπ), where n is an integer,
trig–functions are useful to describe cyclical data.
Circadian Rhythms
Circadian rhythms are the bio–rhythms of a person
or of any living beings, that fluctuate through out
some fixed period of time: hourly, daily, etc..
For people, the measurements could be the blood
pressures, or the heart rates, etc..

105. Important Trigonometric Values
The temperature of a person drops when sleeping
and rises during the day due to activities.
A way to summarize the collected temperature data
is to use a trig–function to model the data.
For example, using the sine formula,
the temperature T might be given as
T(t) = 37.2 – 0.5*sin(πt/12)
where t is the number of hours passed 11 pm
when the person falls asleep.
So at 11 pm, t = 0 the temperature is 37.2o,
at 5 am, t = 6, the temperature drops to 36.7o,
at 11 am, t = 12, the temperature rises back to 37.2o,
and at 5 pm, t = l8, the temperature peaks at 37.7o.
This gives a convenient estimation of the temperature.

106. Important Trigonometric Values
https://en.wikipedia.org/
wiki/Trigonometric_funct
ions#sec
We utilize the following angles and coordinates on
the unit circle for examples and homework.
One should memorize them.

107. Important Trigonometric Values
1. Fill in the angles and the coordinates of
points on the unit circle
a. in the four diagonal directions and
b. in the twelve hourly directions.
(See the last slide.)
2.
Convert the angles into degree and
find their values. If it’s undefined, state So. (No calculator.)
sin(4π)cos(2π), tan(3π),sec(–2π), cot(–3π),csc(–π),
3. cos(2π), tan(π),sec(–3π), cot(–5π),csc(–2π), sin (–3π)
4. cos(π /2), tan(3π/2),sec(–π/2), cot(–3π /2),
cot(–5π/2),csc(–π/2),sin(–π/2),5. sec(–π/2),
7. cos(–11π/4),
tan(7π/4),
sec(–7π/4),cot(5π/4),
cot(5π/4),
csc(π/4),
sin(–π/4),6. sec(–3π/4),

108. Important Trigonometric Values
9. cos(–2π/3),
tan(7π/3),
sec(–7π/3),cot(5π/3),
cot(5π/3),
csc(4π/3),
sin(–π/3),8. sec(–2π/3),
11. cos(–23π/6),
tan(7π/6),
sec(–17π/6),cot(25π/6),
cot(5π/6),
csc(–5π/6),
sin(–π/6),10. sec(–5π/6),
12. a. Draw and find the locations on the unit circle where
cos() = 1/3. b. If tan() is positive, find tan().
13. a. Draw and find the locations on the unit circle where
tan() = 1/3. b. If sec() is positive, find sin().
14. a. Draw the and find locations on the unit circle where
csc() = –4. b. If cot() is positive, find cos().
15. a. Draw and find the locations on the unit circle where
cot() = –4/3. b. If sin() is positive, find sec().
16. a. Draw and find the locations on the unit circle where
sec() = –3/2. b. If tan() is positive, find sin().

109. Important Trigonometric Values
17. a. Draw the locations on the unit circle where cos() = a.
b. If tan() is positive, find tan() in terms of a.
18. a. Draw the locations on the unit circle where tan() = 2b.
b. If sec() is positive, find sin() in terms of b.
19. a. Draw the locations on the unit circle where cot() = 3a.
b. If sin() is positive, find sec() in terms of a.
20. a. Draw the locations on the unit circle where sec() = 1/b.
b. If tan() is positive, find sin() in terms of b.
21. Justify the tangent and
the cotangent are the
distances shown.

110. Important Trigonometric Values
Answers
For problem 1. See Side 106
For problems 2–11, verify your answers with a calculator.
b. sec() = –5/4.b. sin() = 1/√10
13.
(3/√10 , 1/√10)
(–3/√10 , –1/√10)
15. (–4/5, 3/5)
(4/5, –3/5)
b. Sec() = 1 + 9𝑎2 / 3a
19.
(−3a/ 1 + 9𝑎2 , –1/ 1 + 9𝑎2)
for a > 0
(3a/ 1 + 9𝑎2 , 1/ 1 + 9𝑎2)
b. Tan() = 1 − 𝑎2 / a
17.
for a > 0
(a , 1 − 𝑎2)
(−a ,− 1 − 𝑎2)