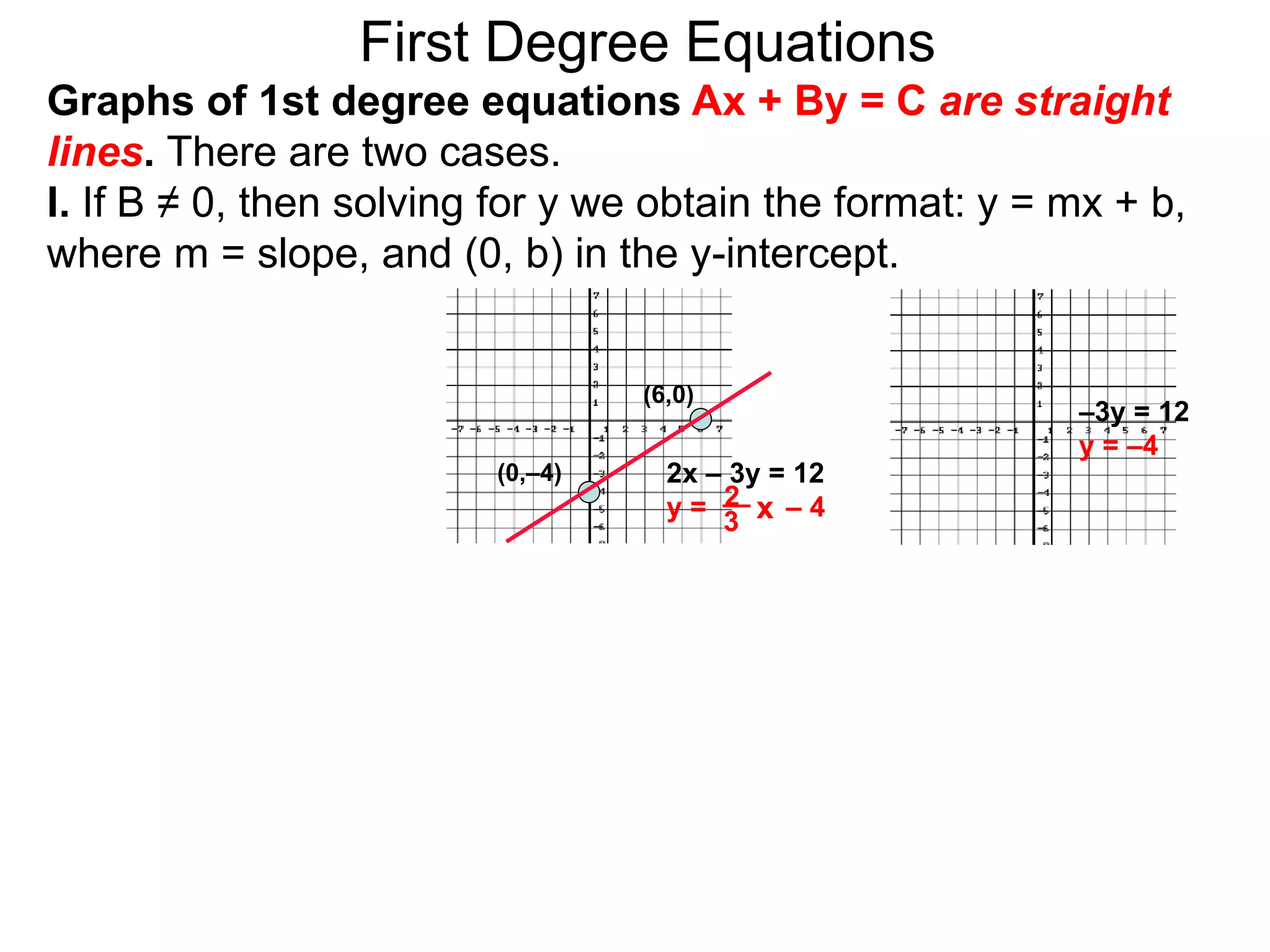
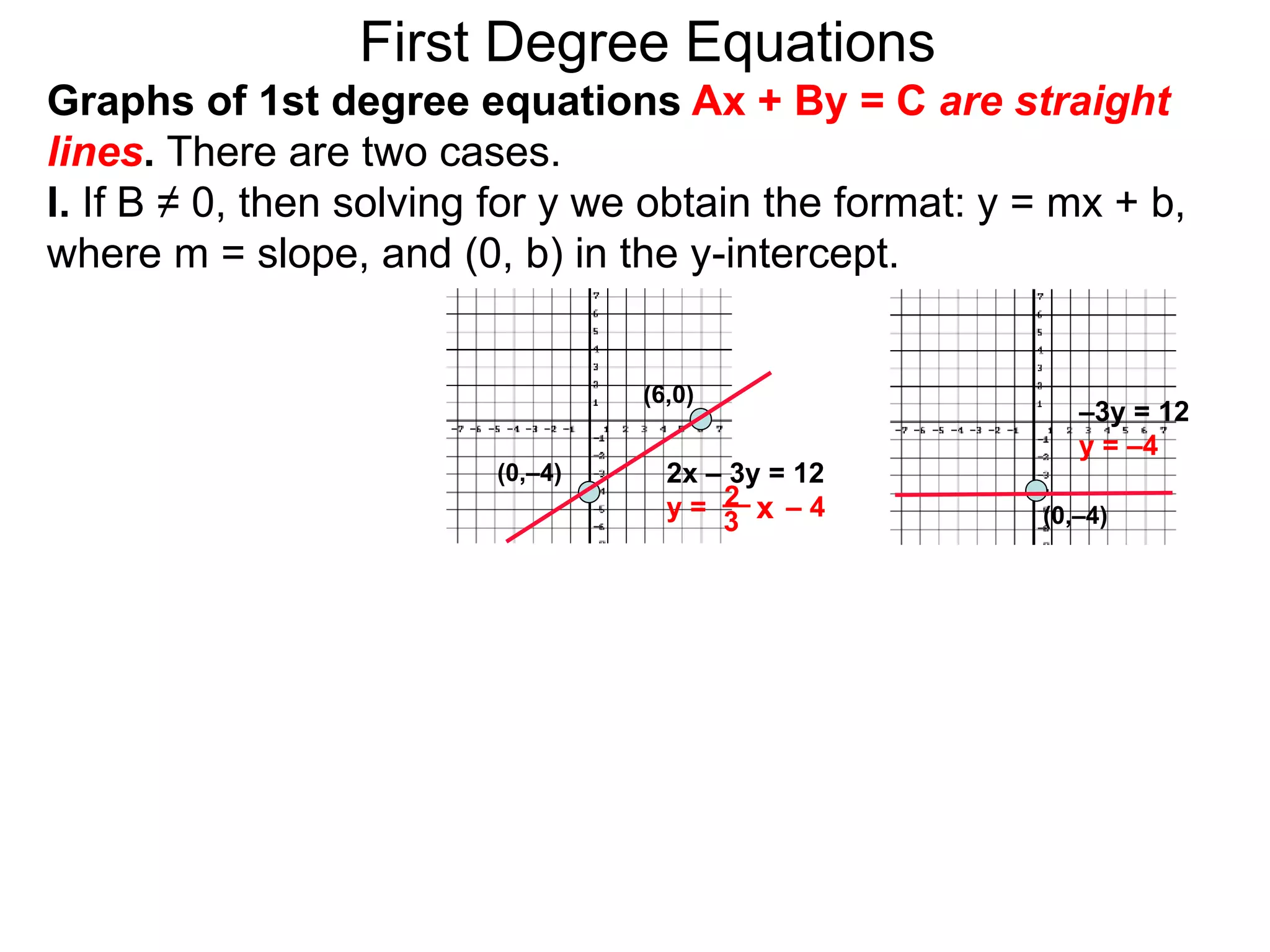
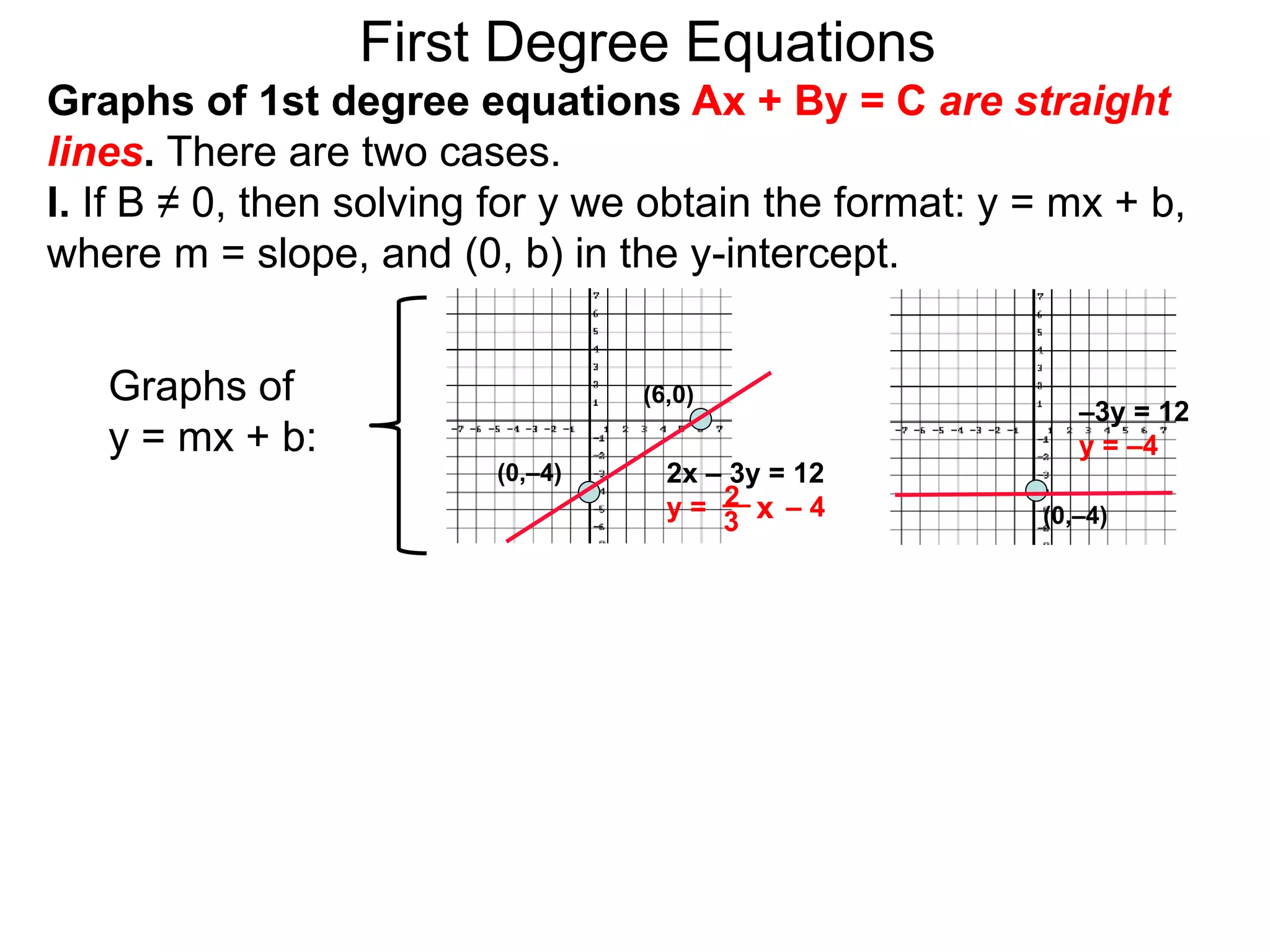
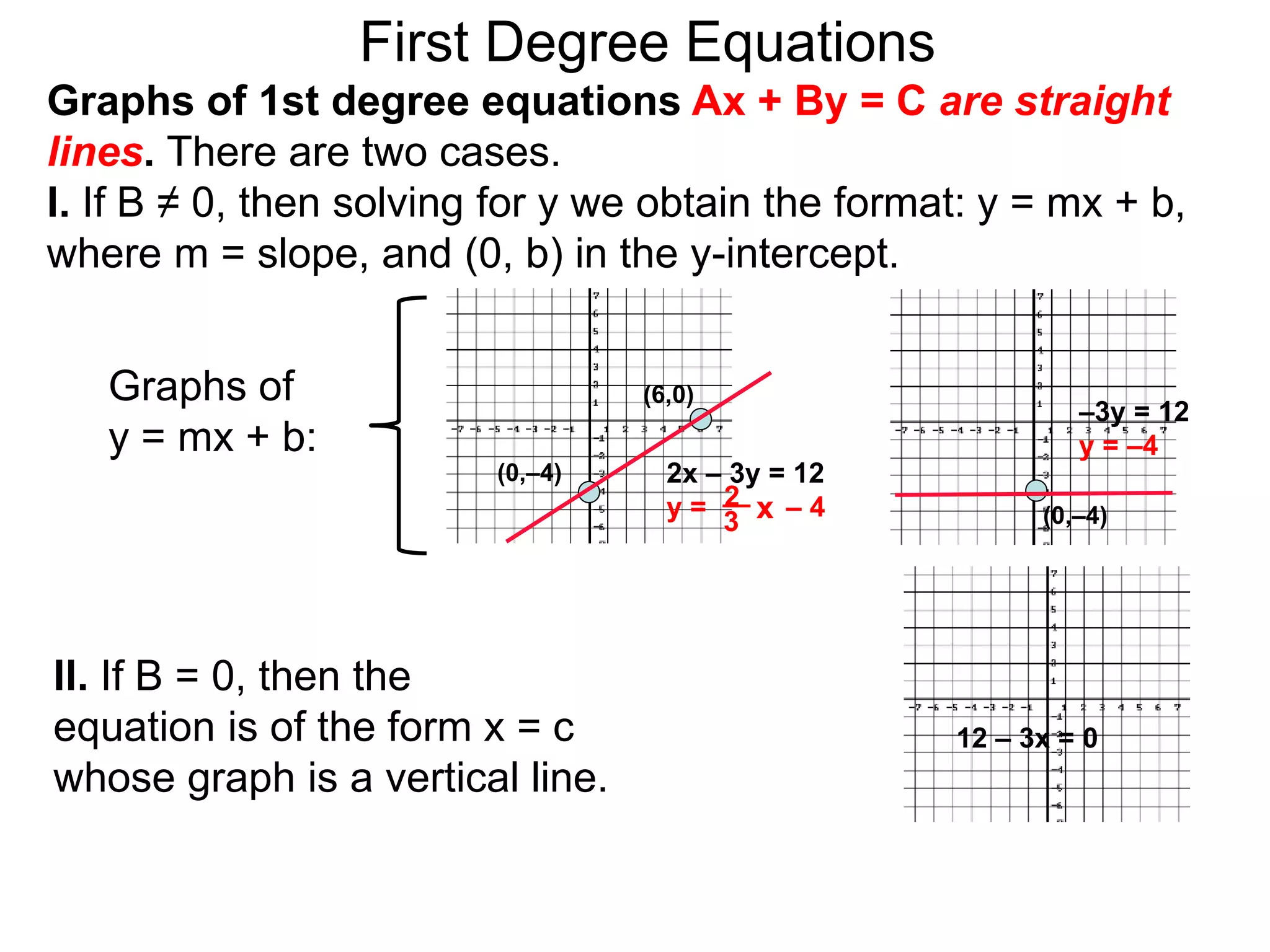
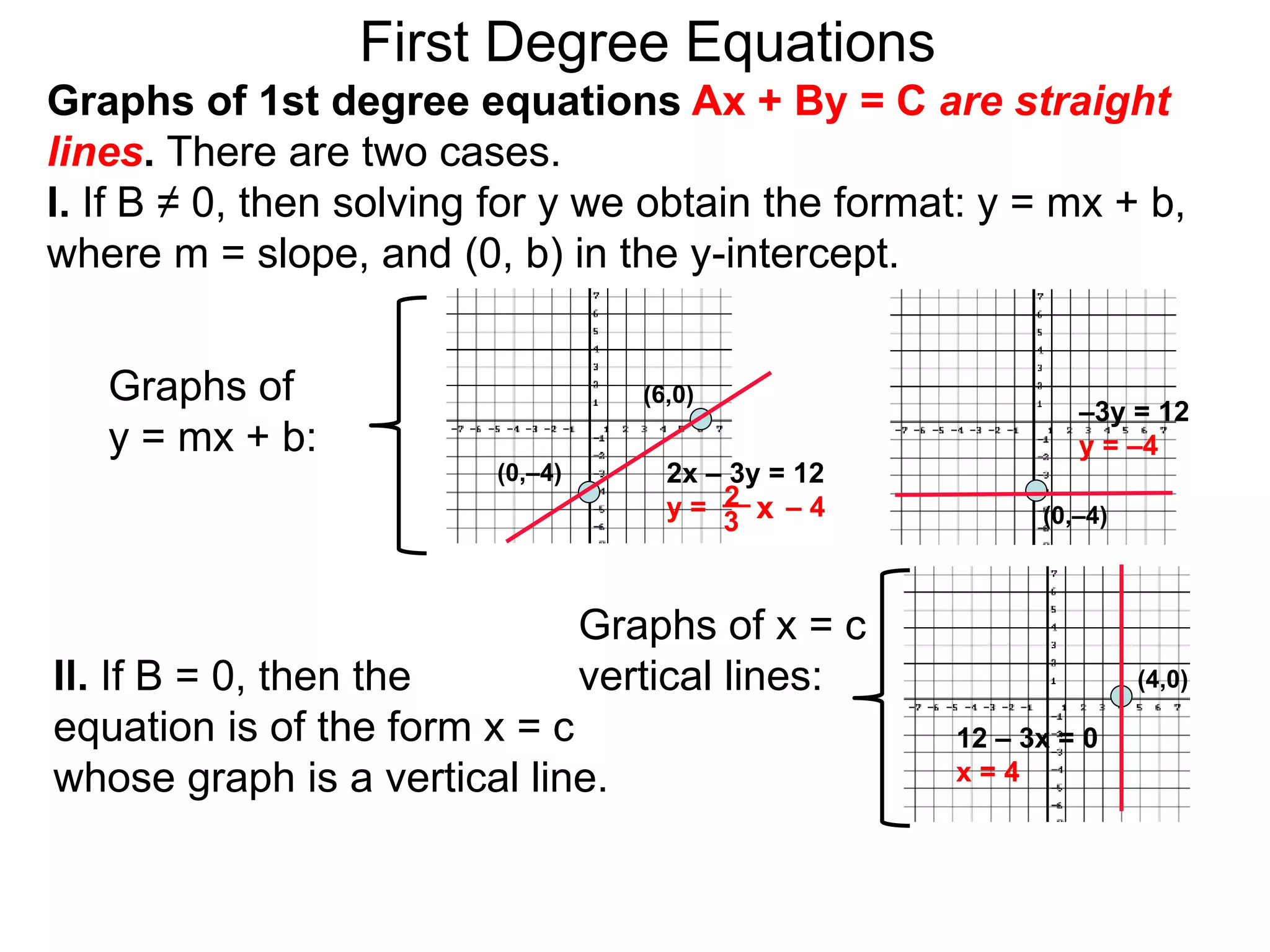
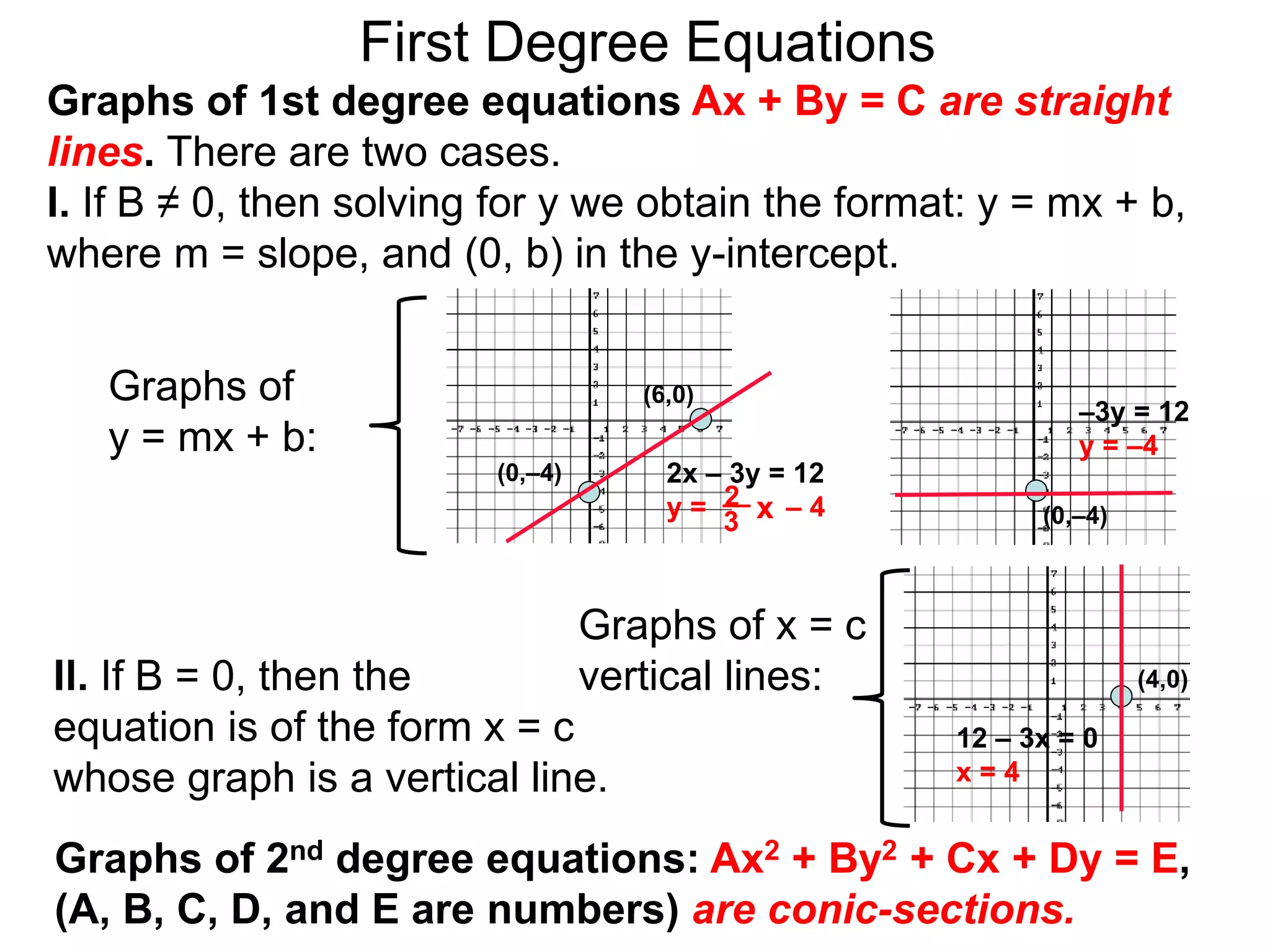
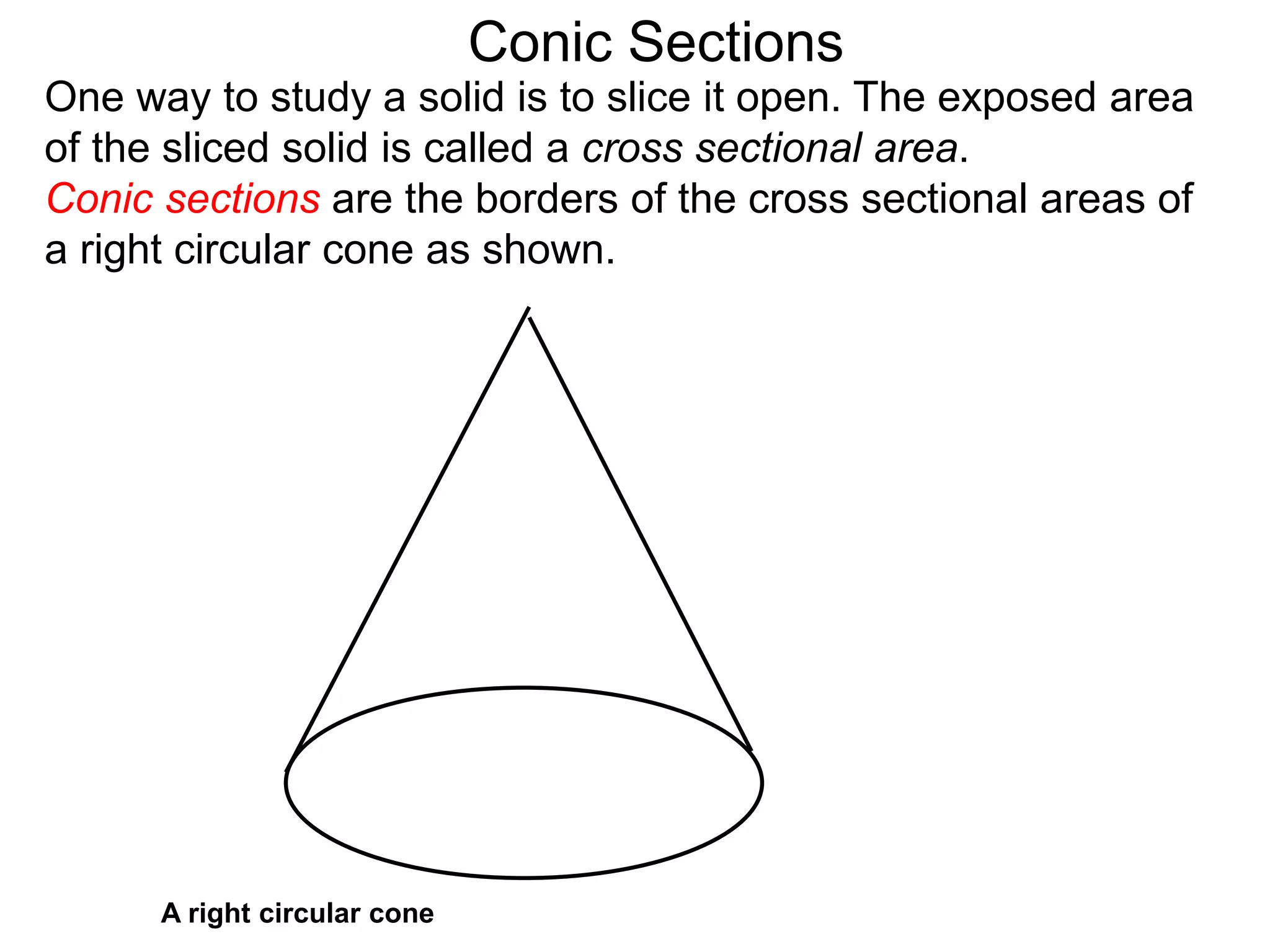
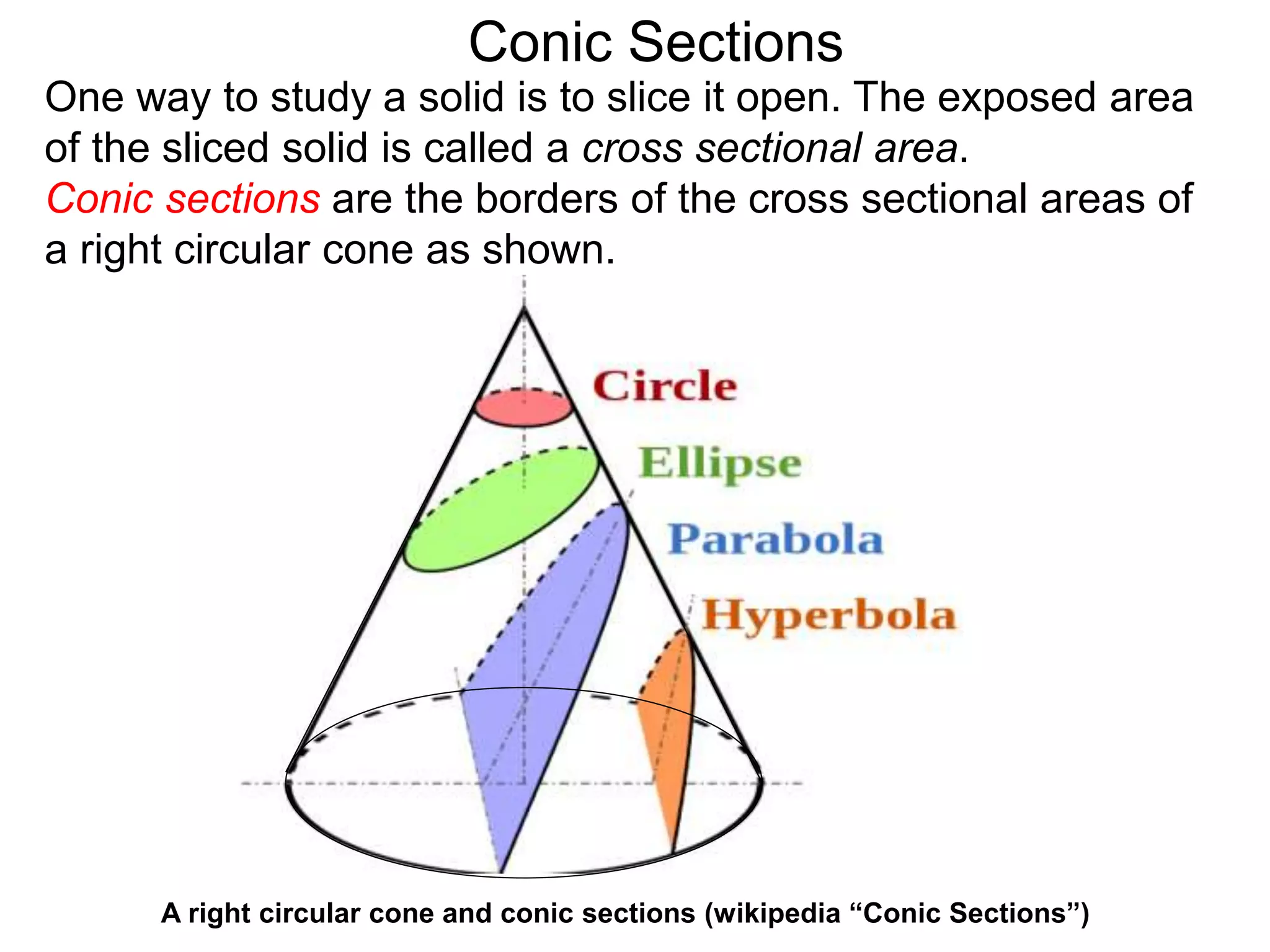
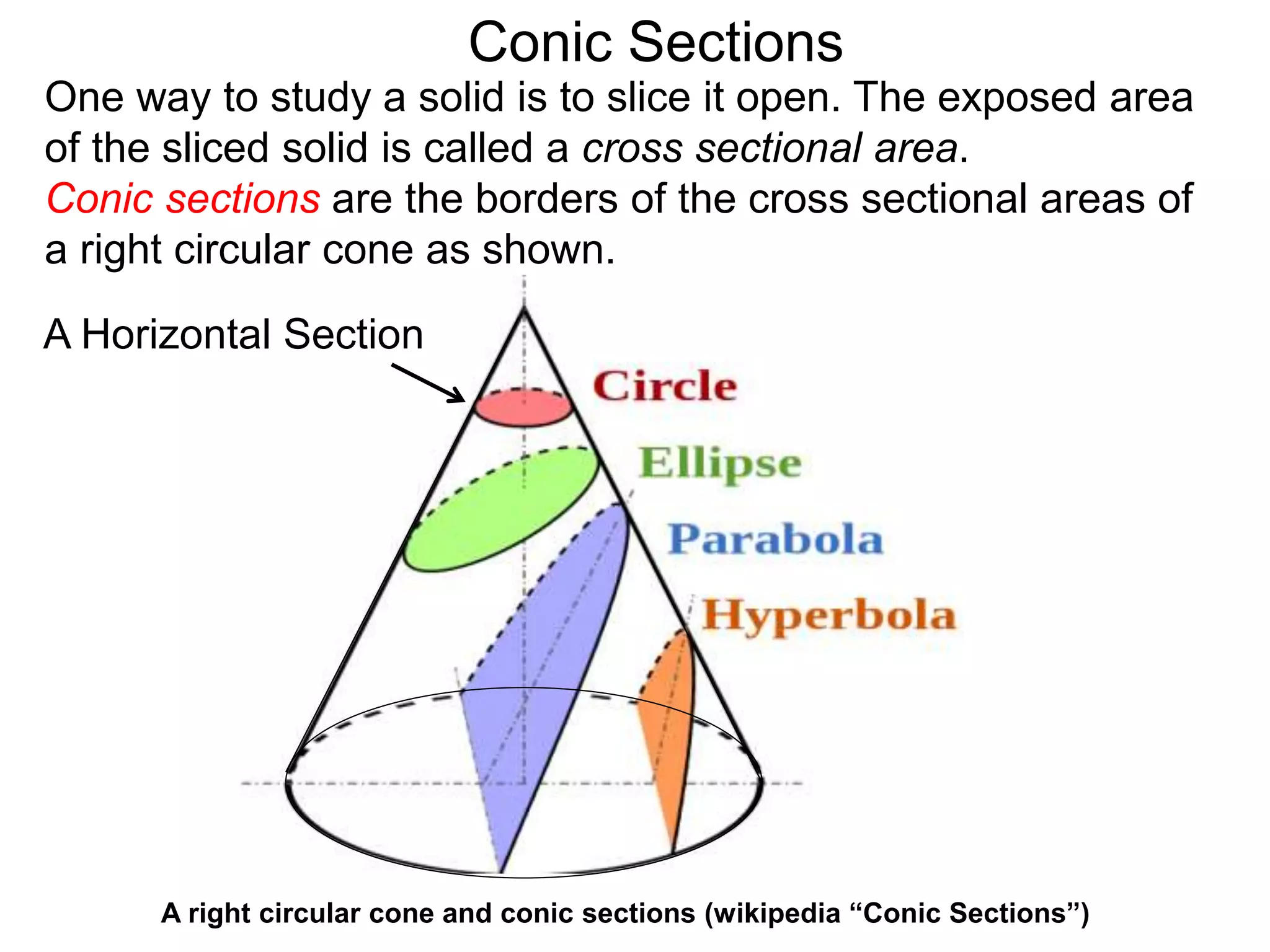
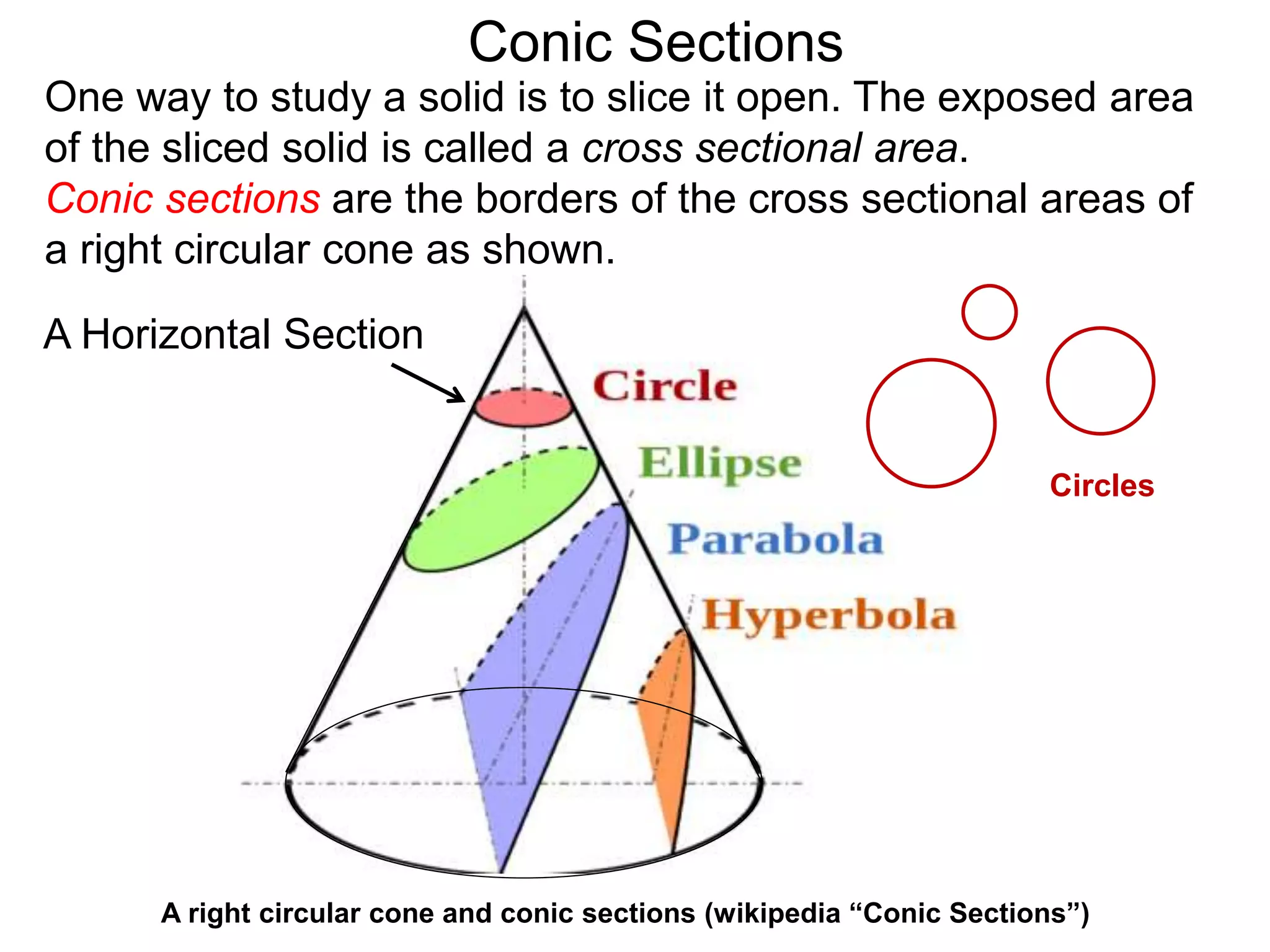
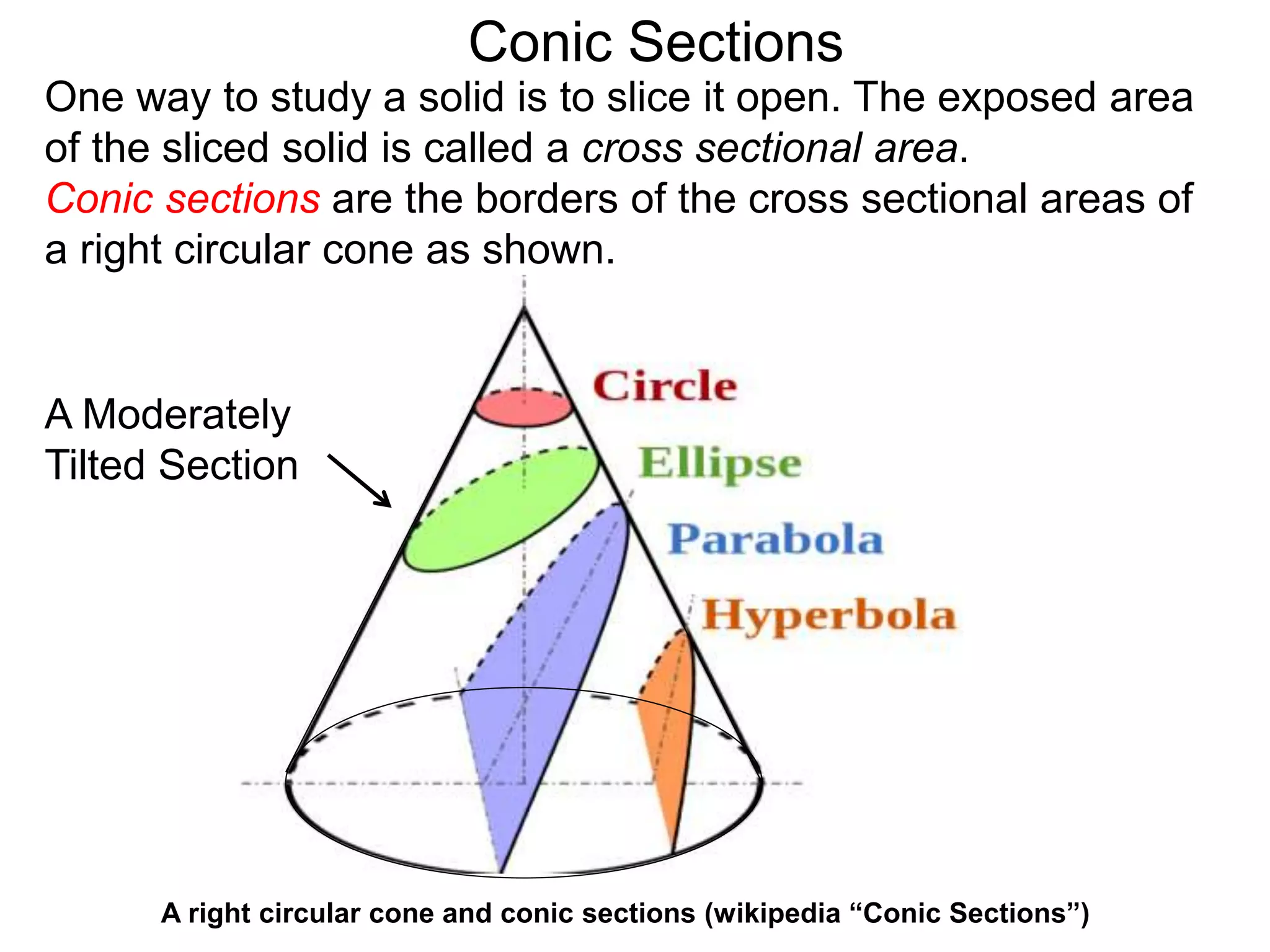
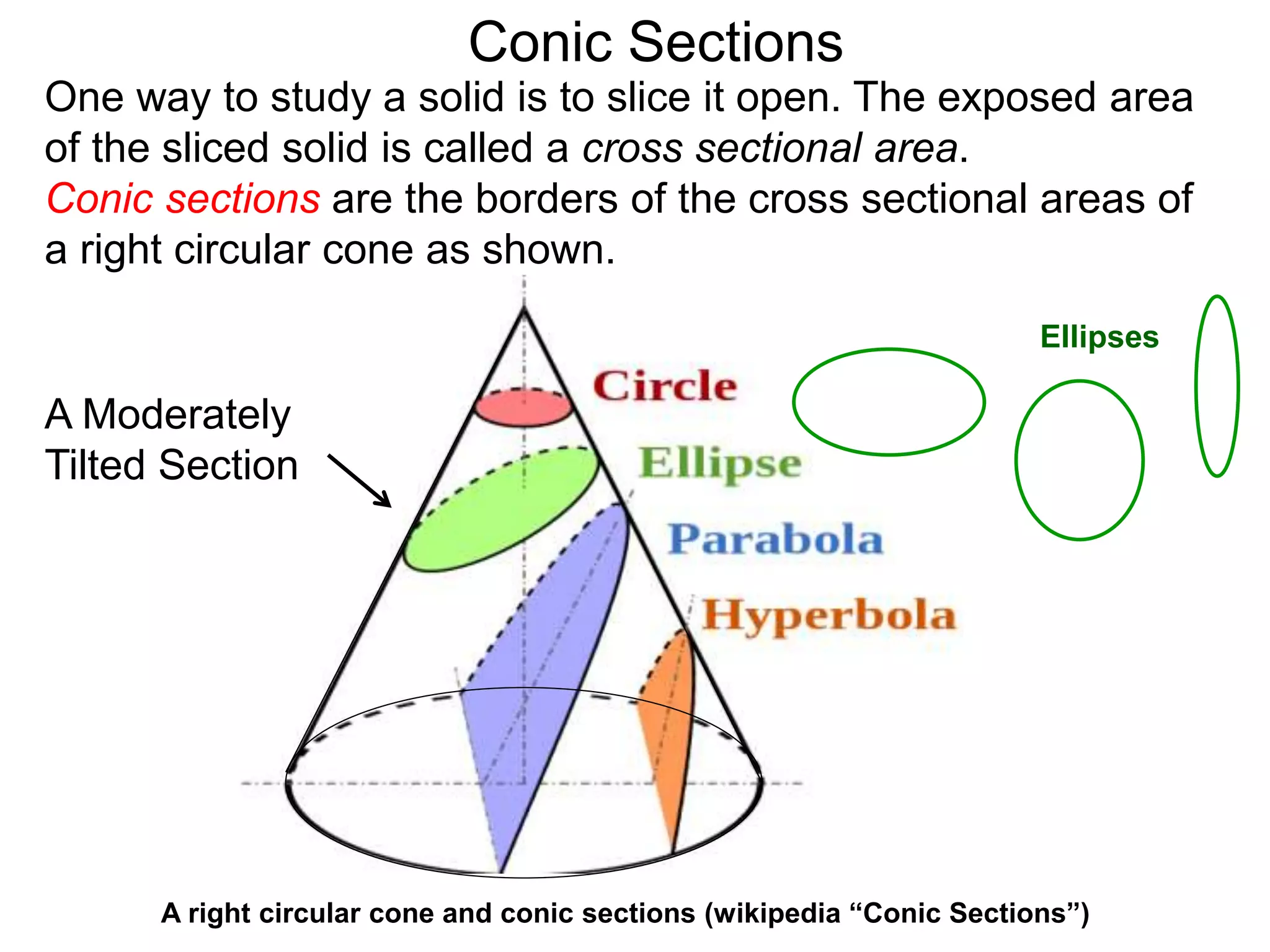
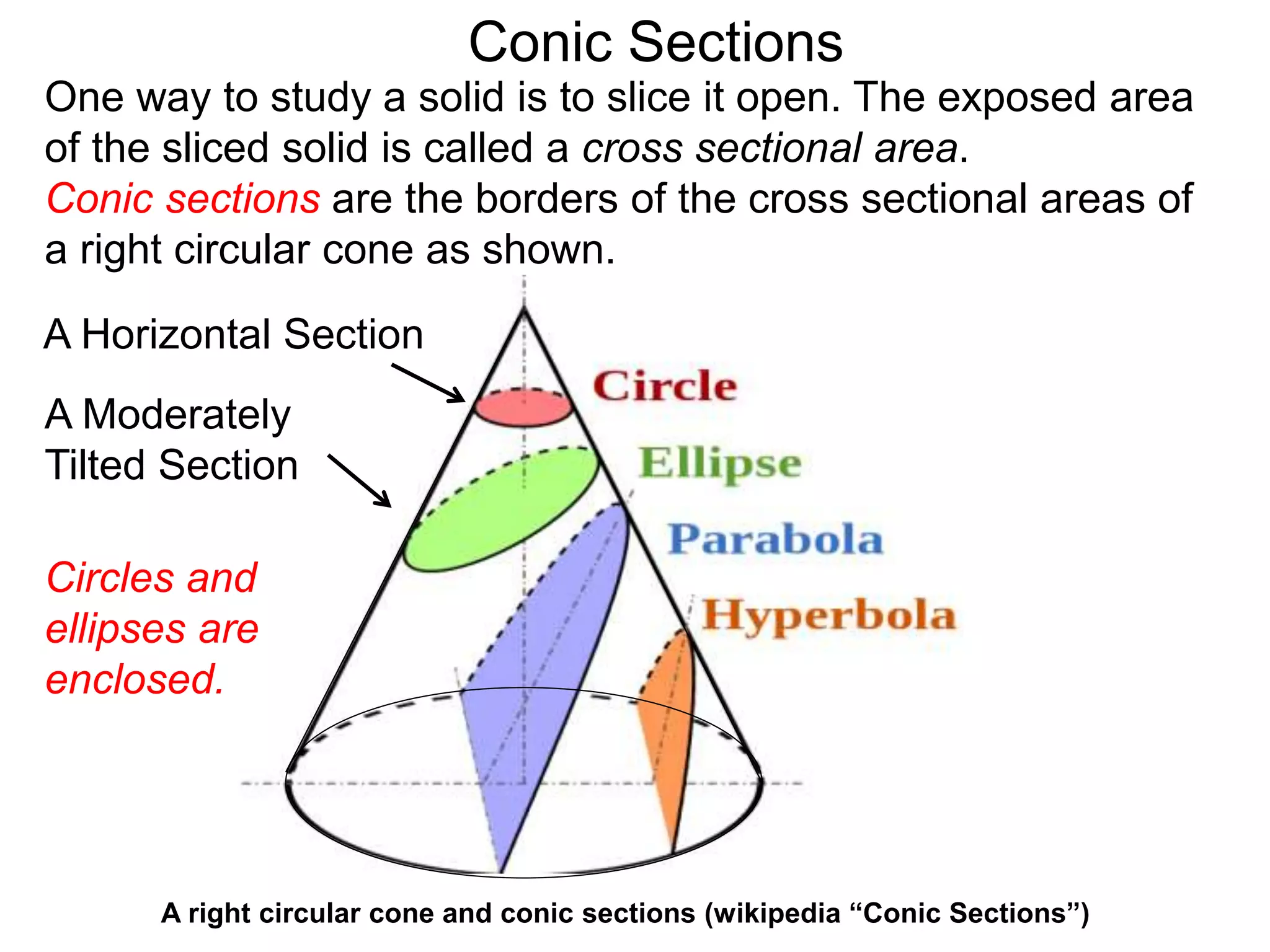
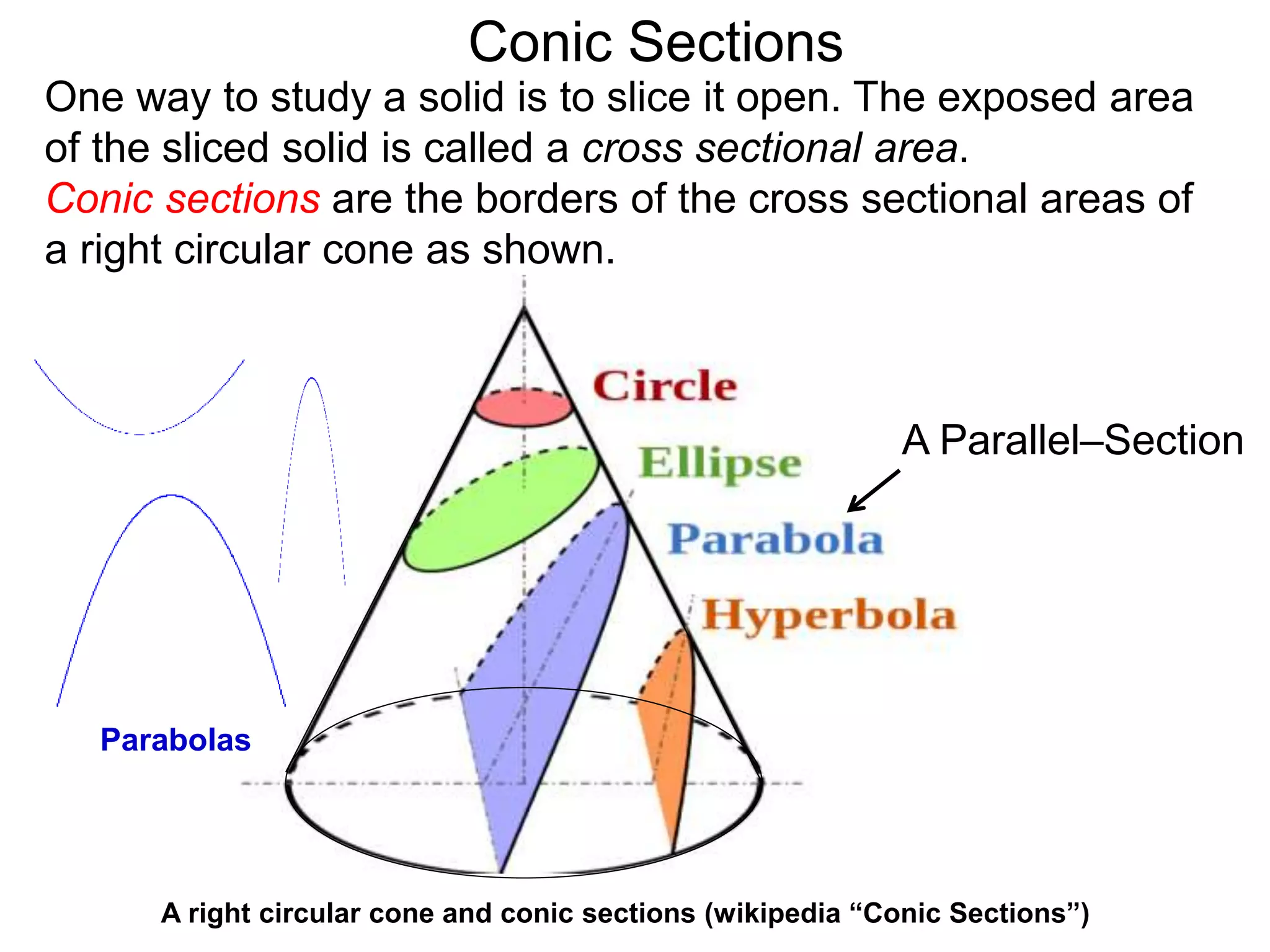
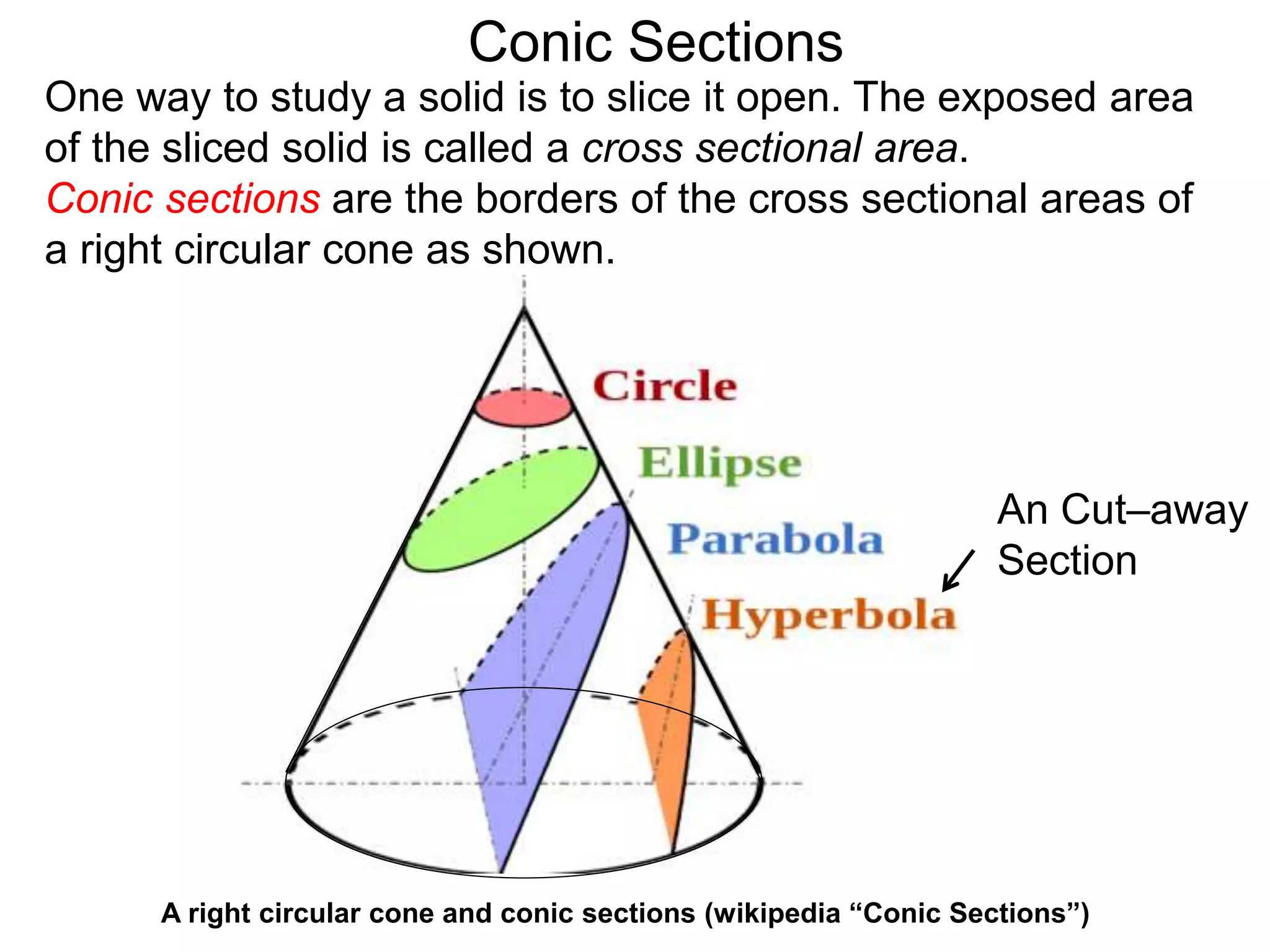
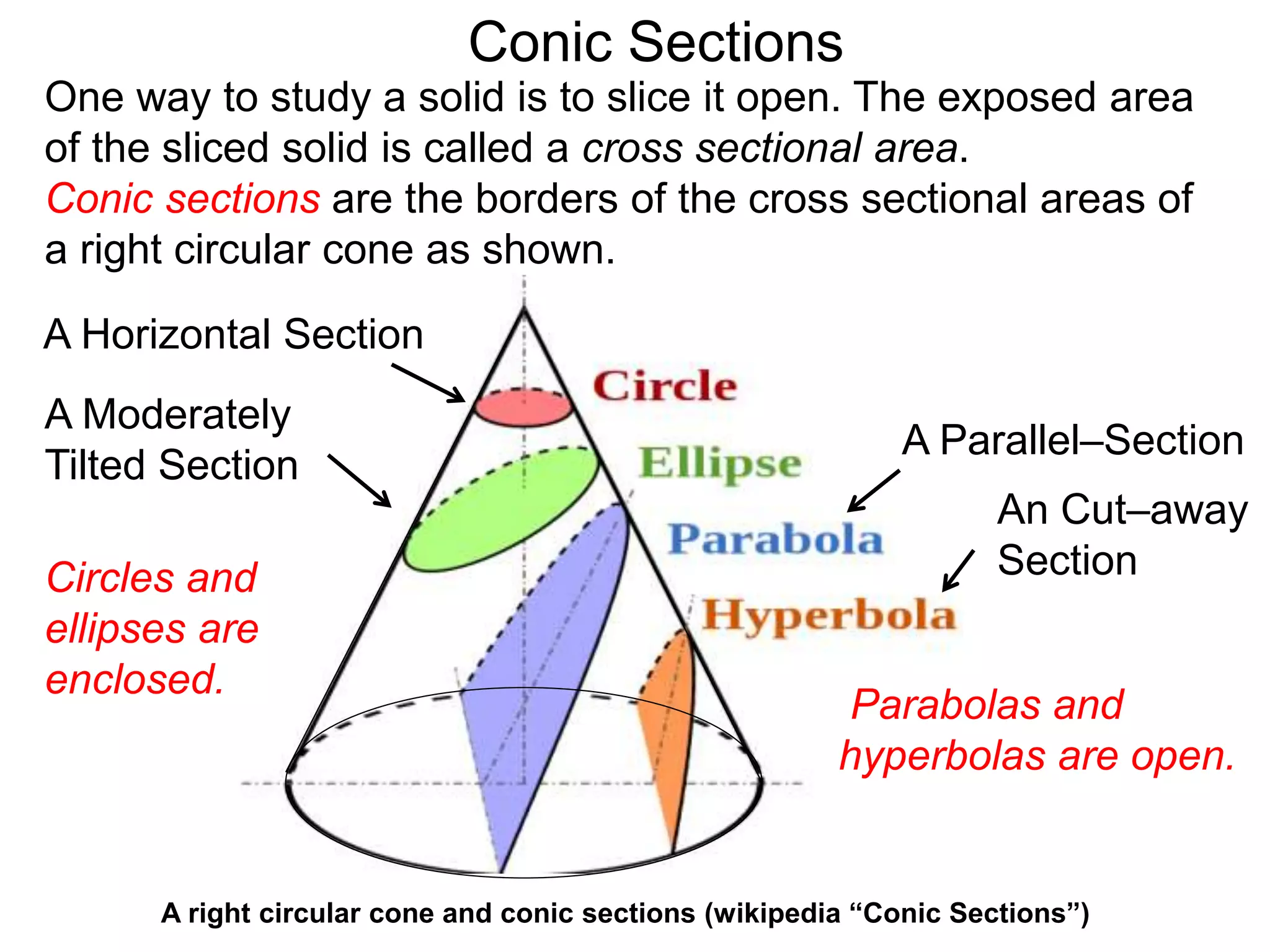
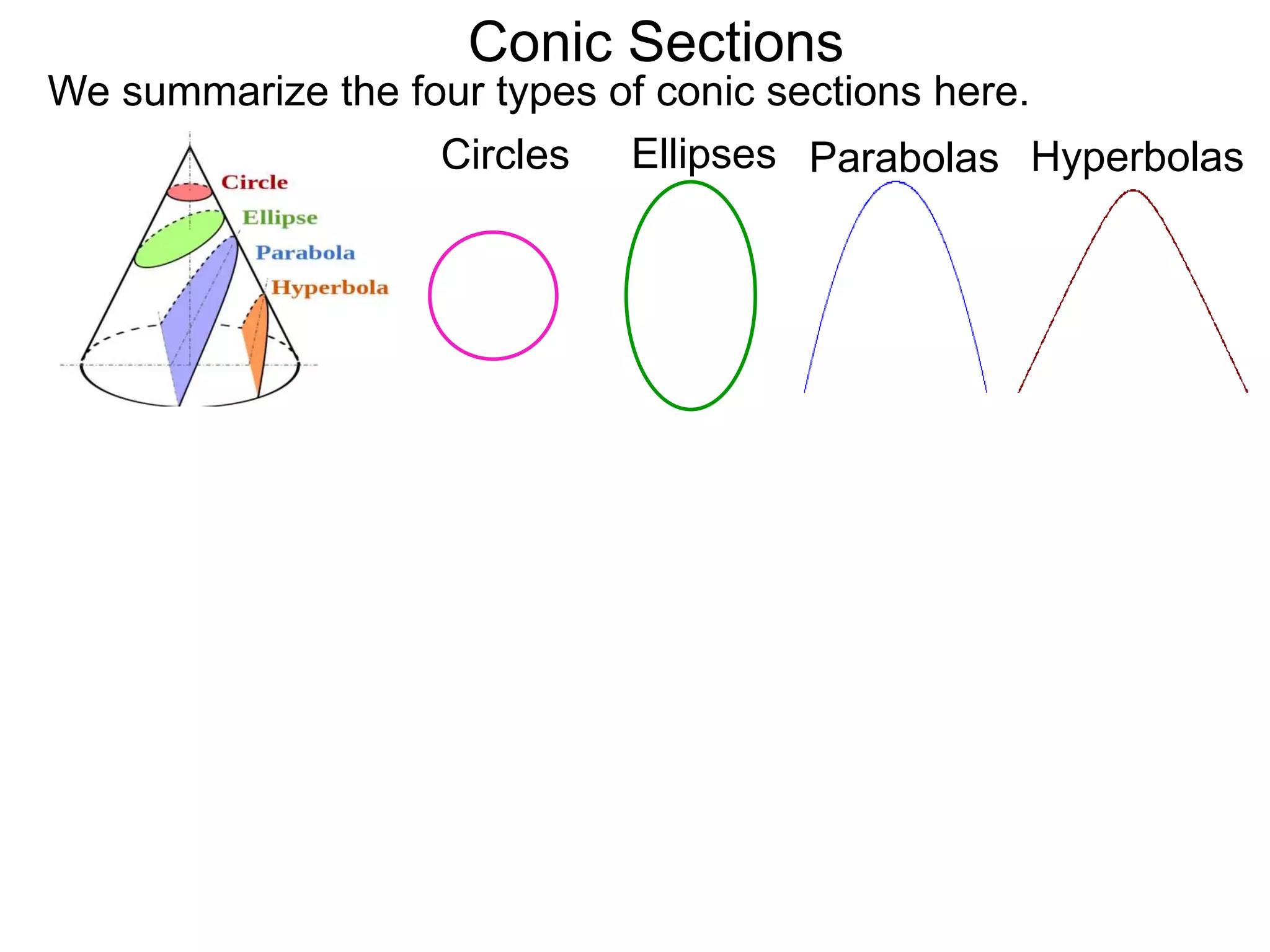
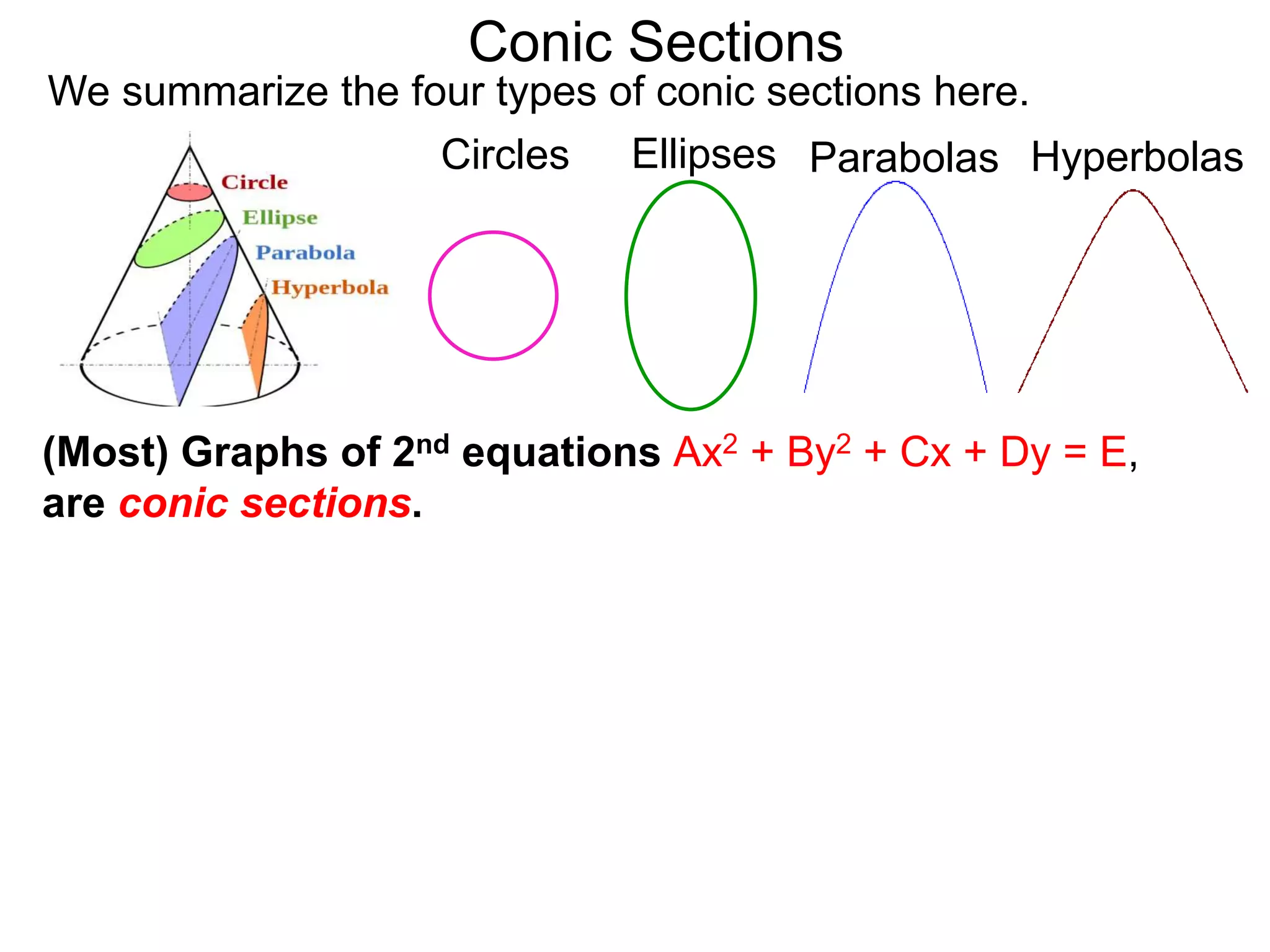
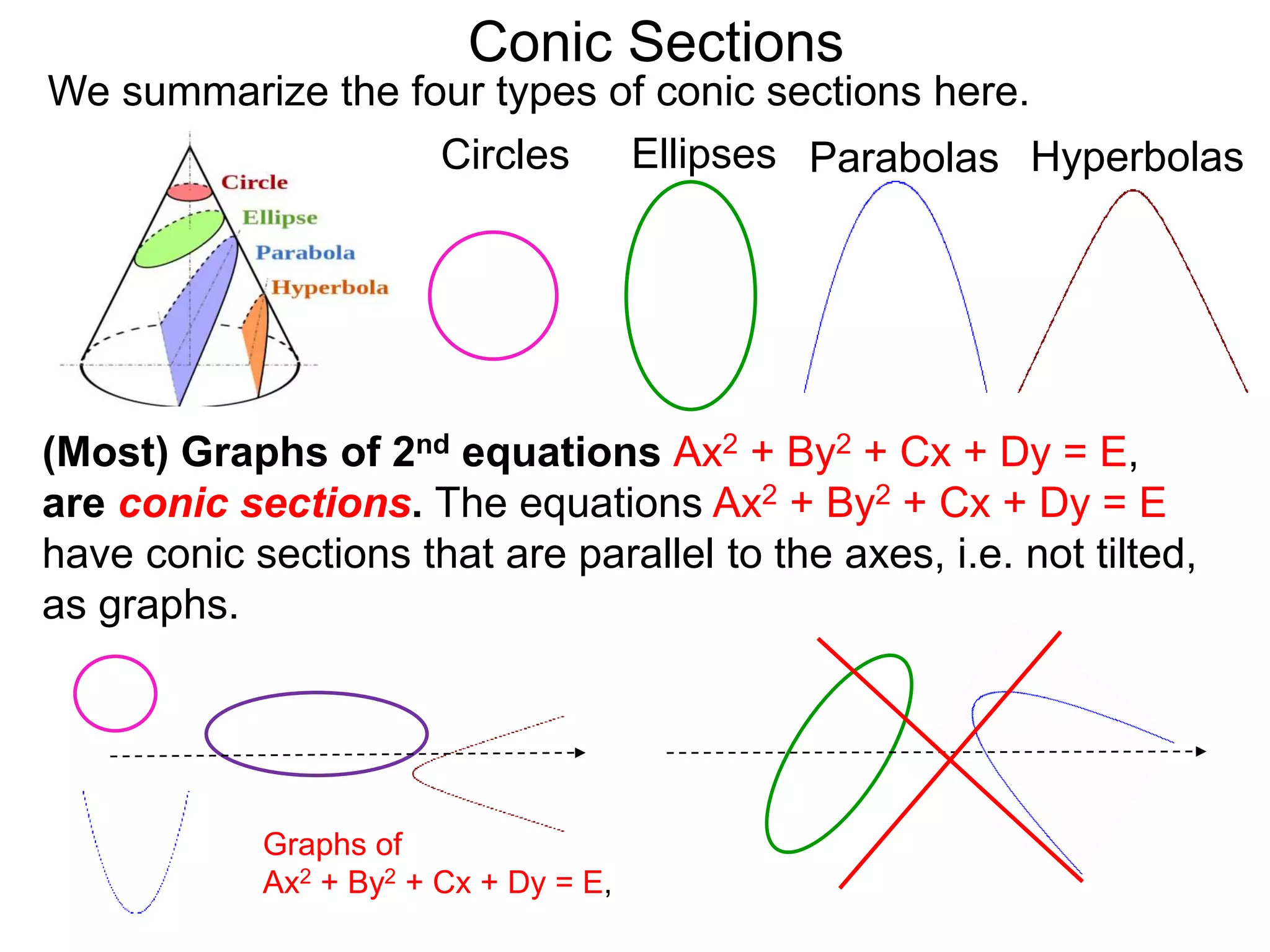
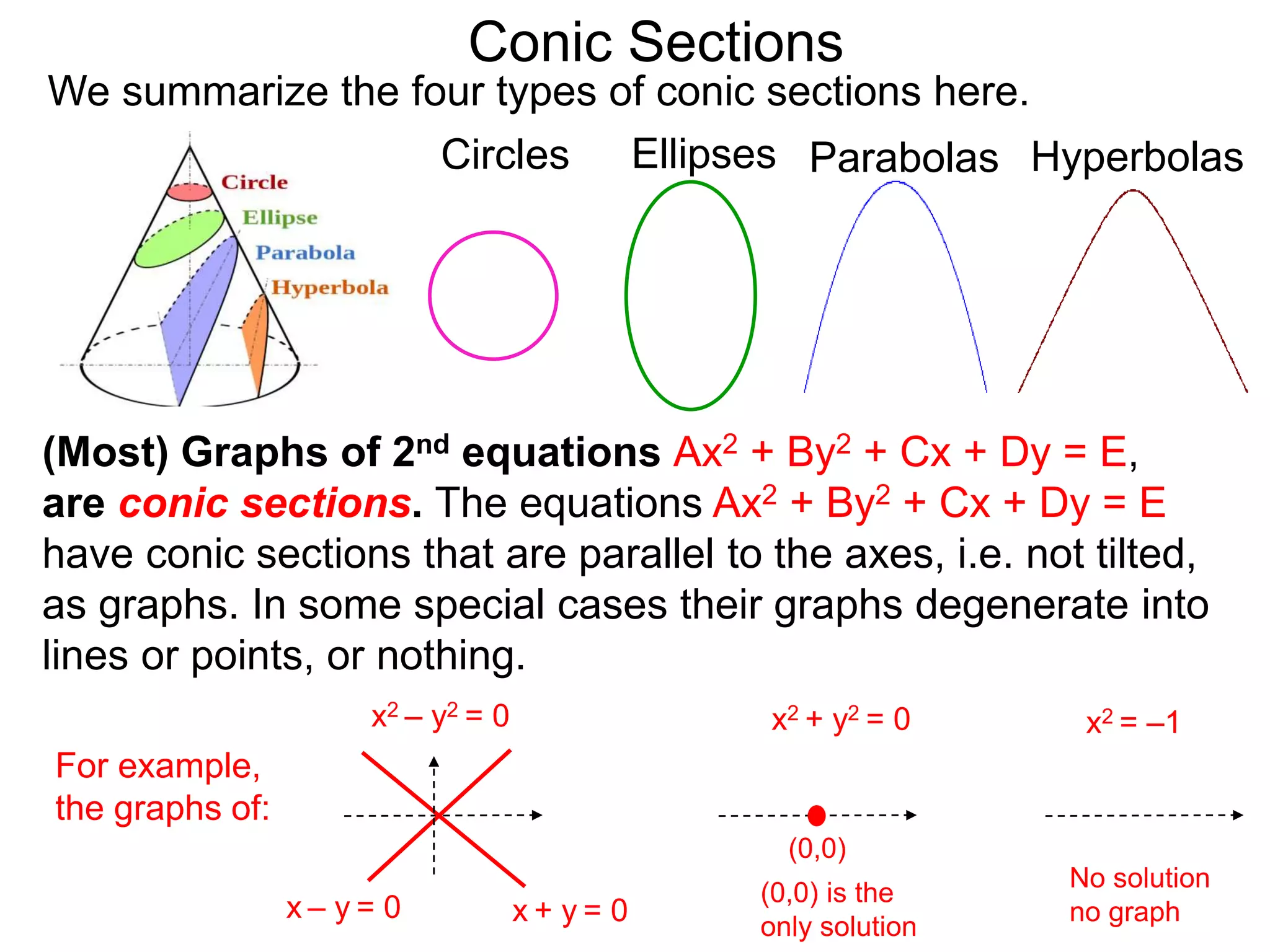
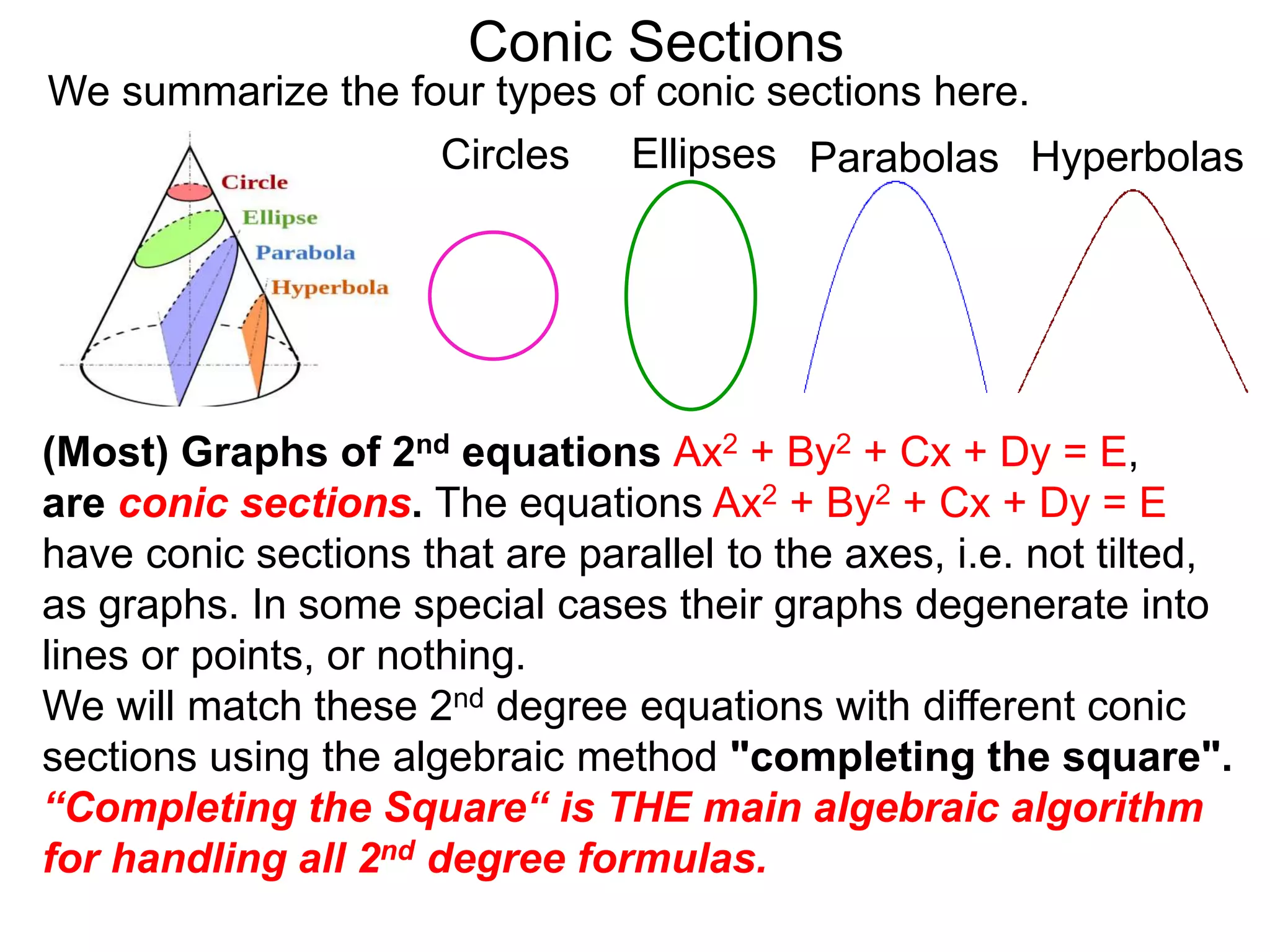
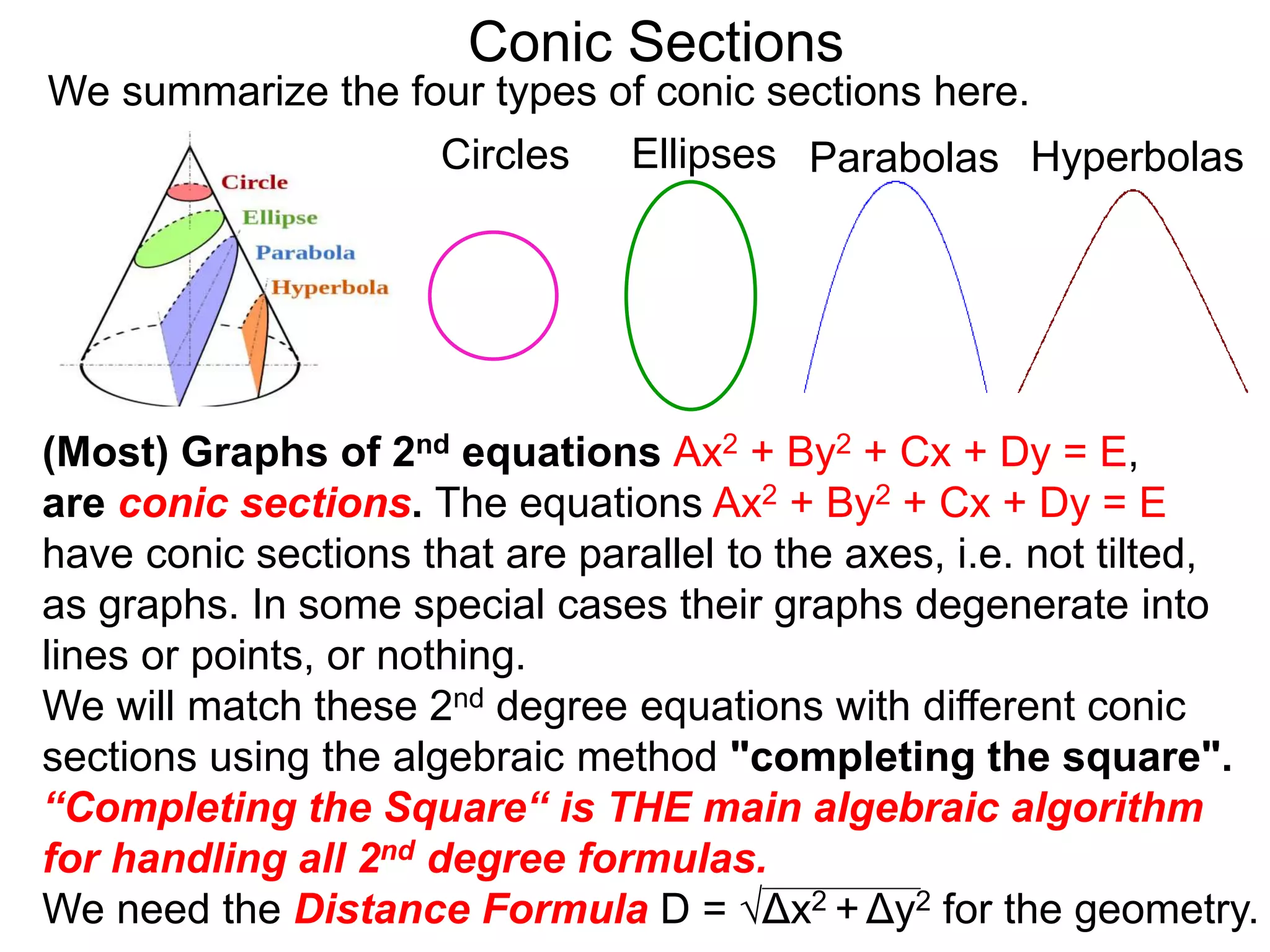
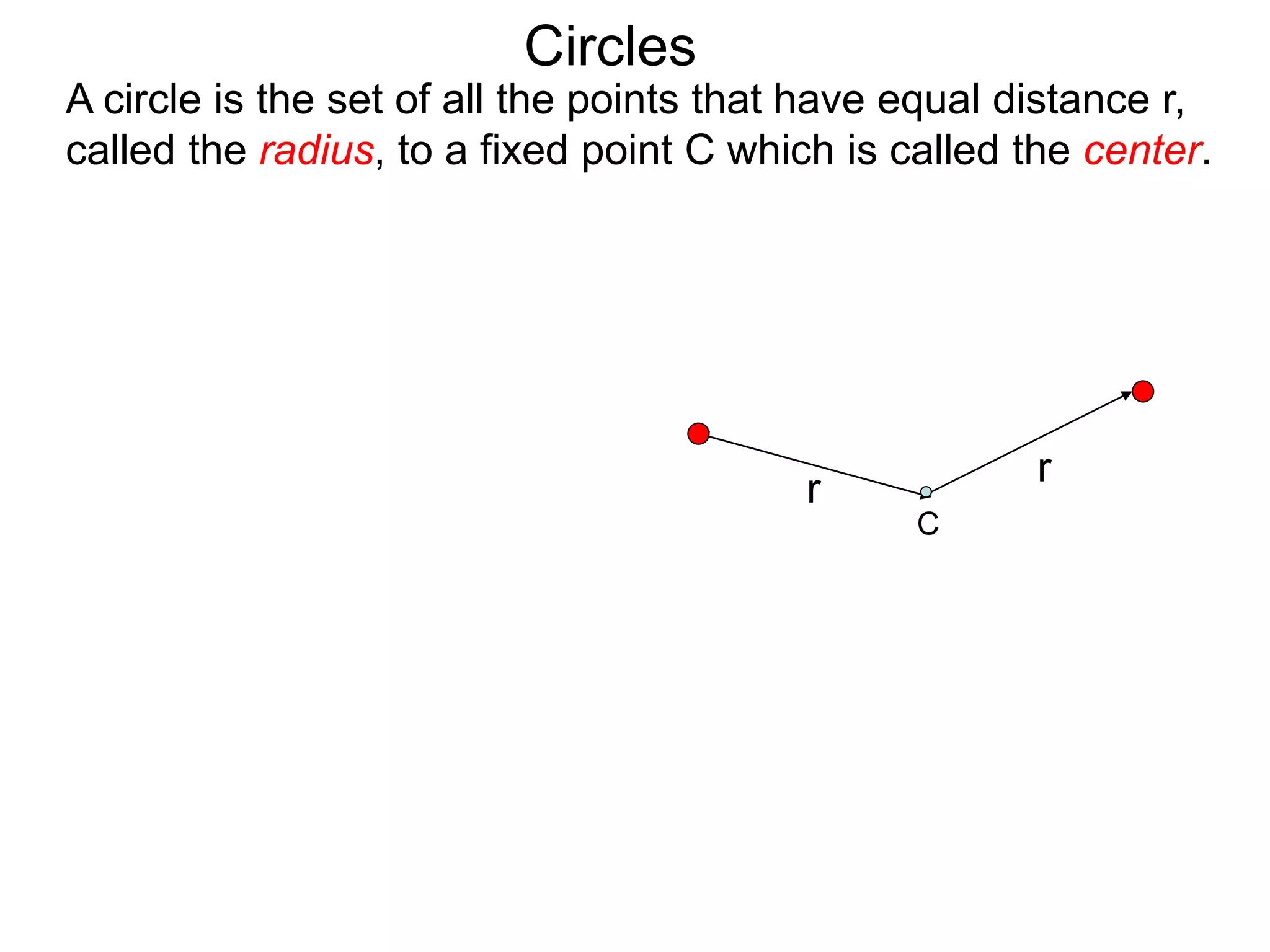
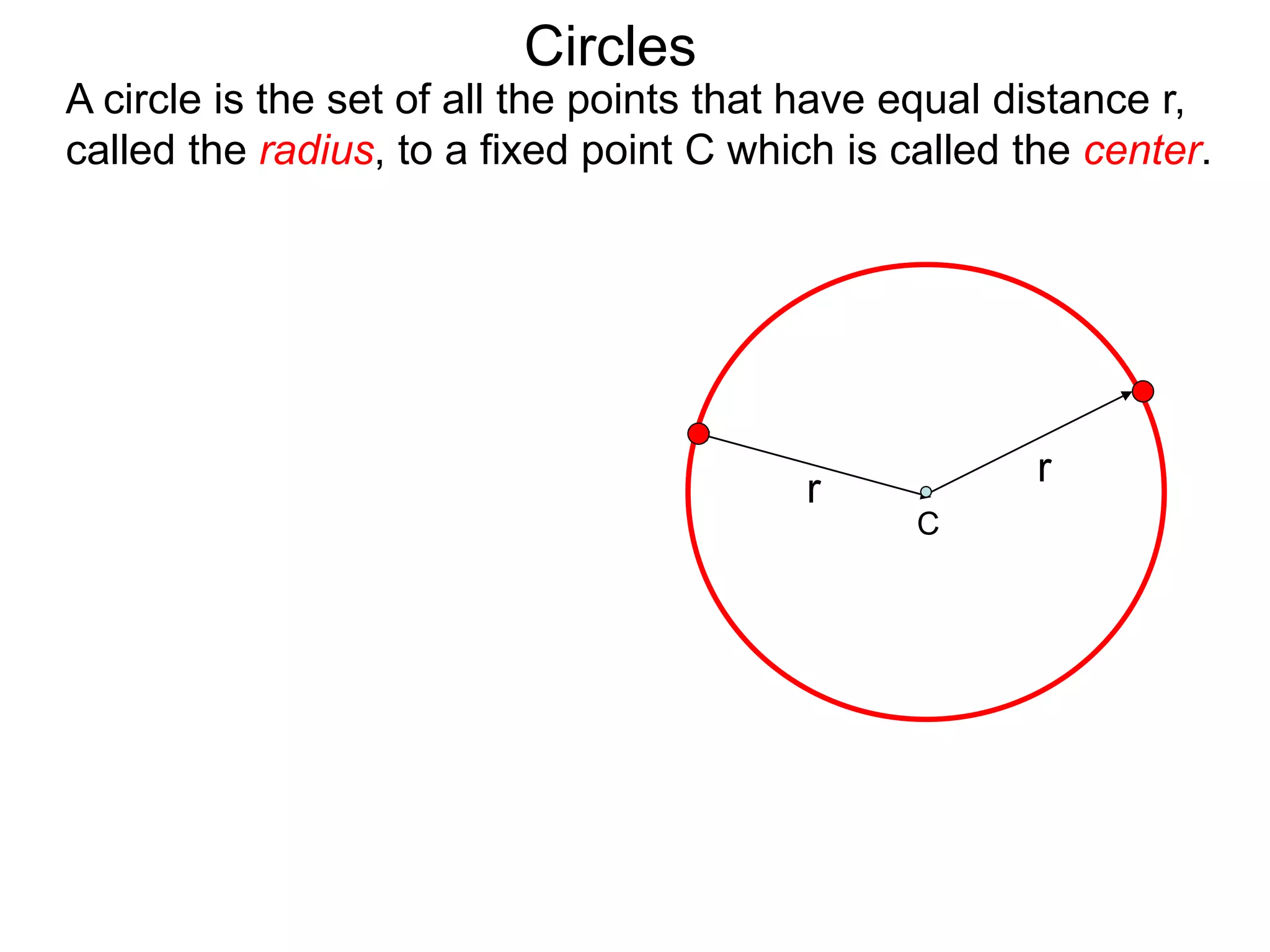
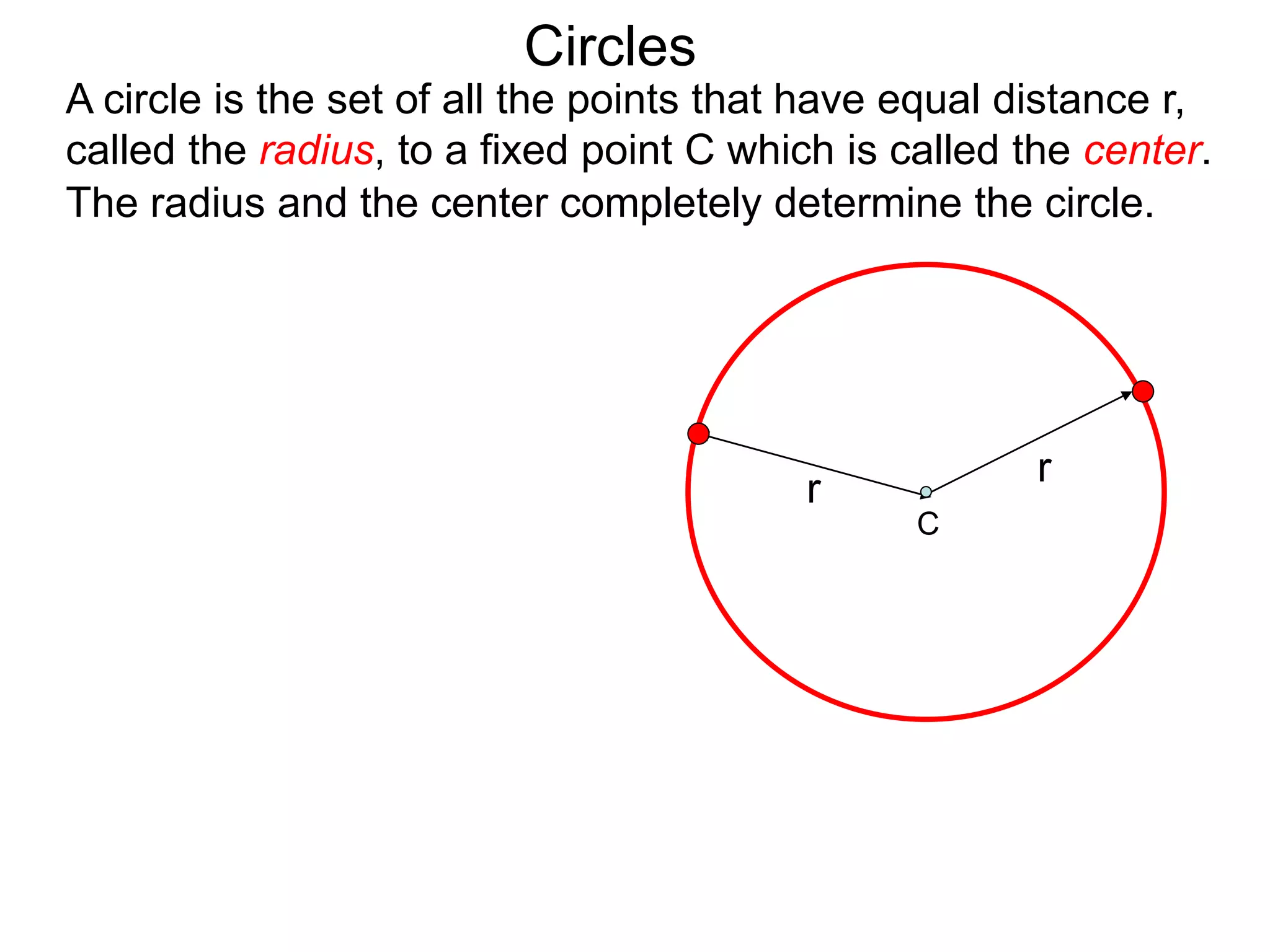
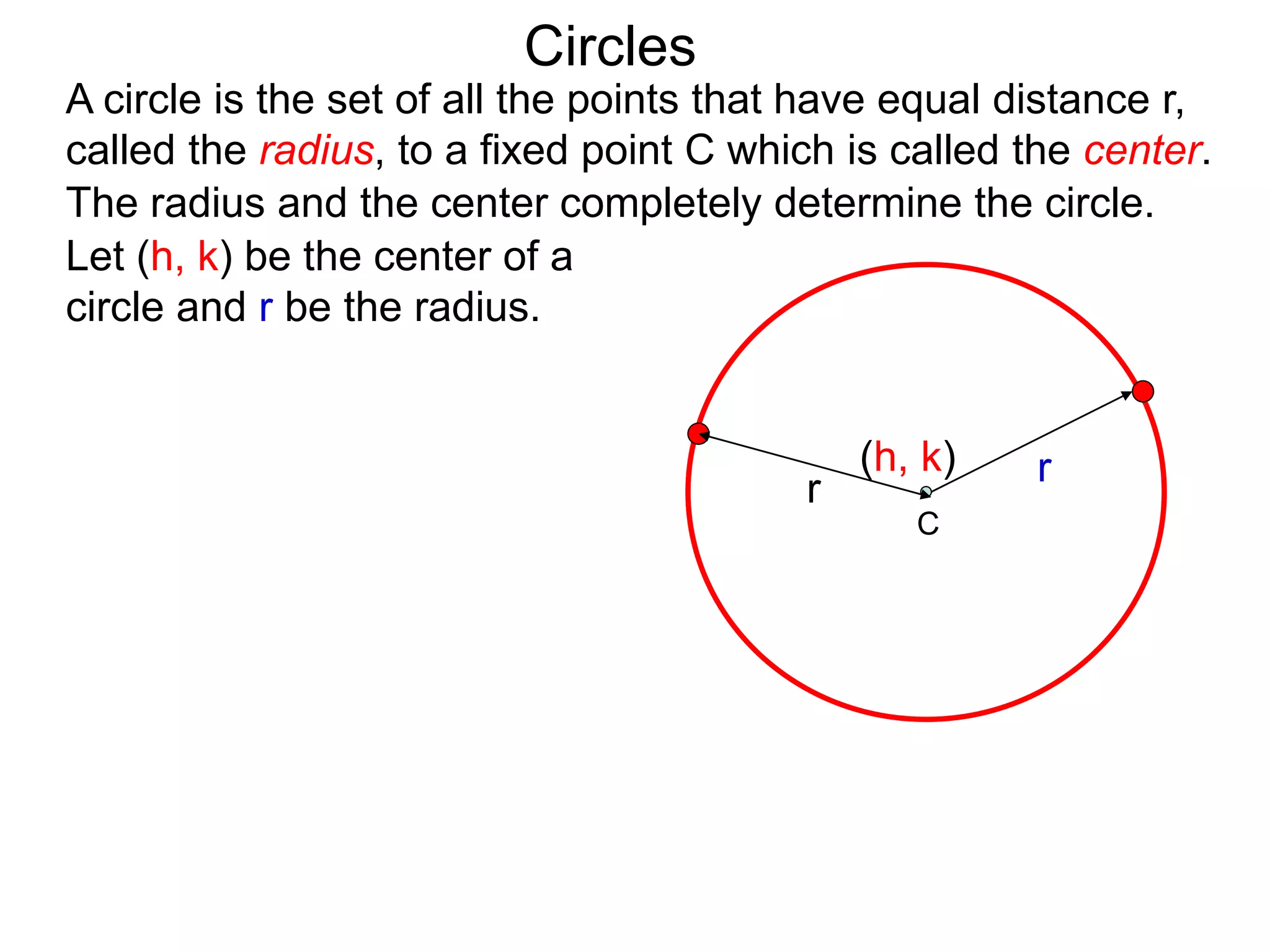
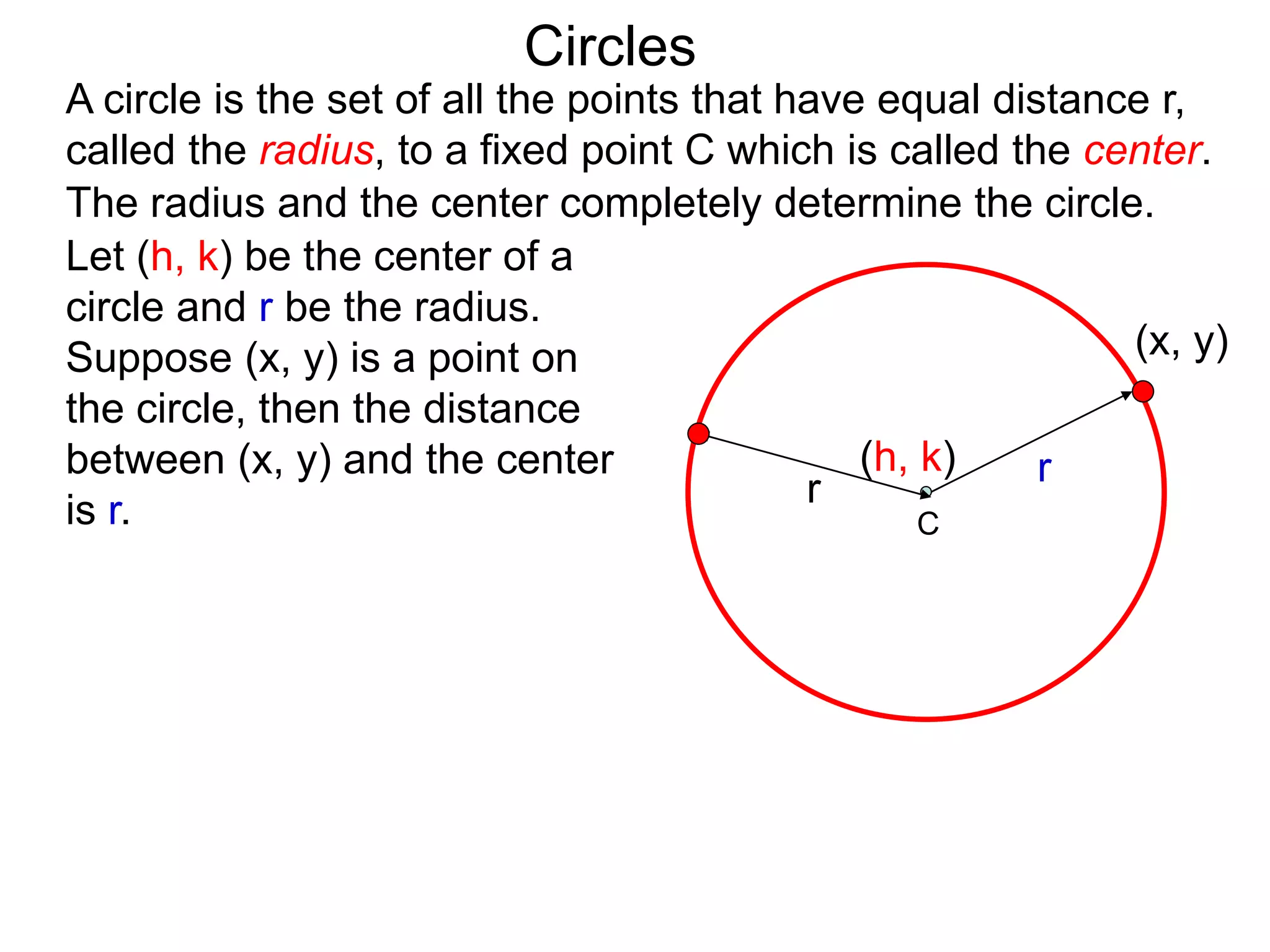
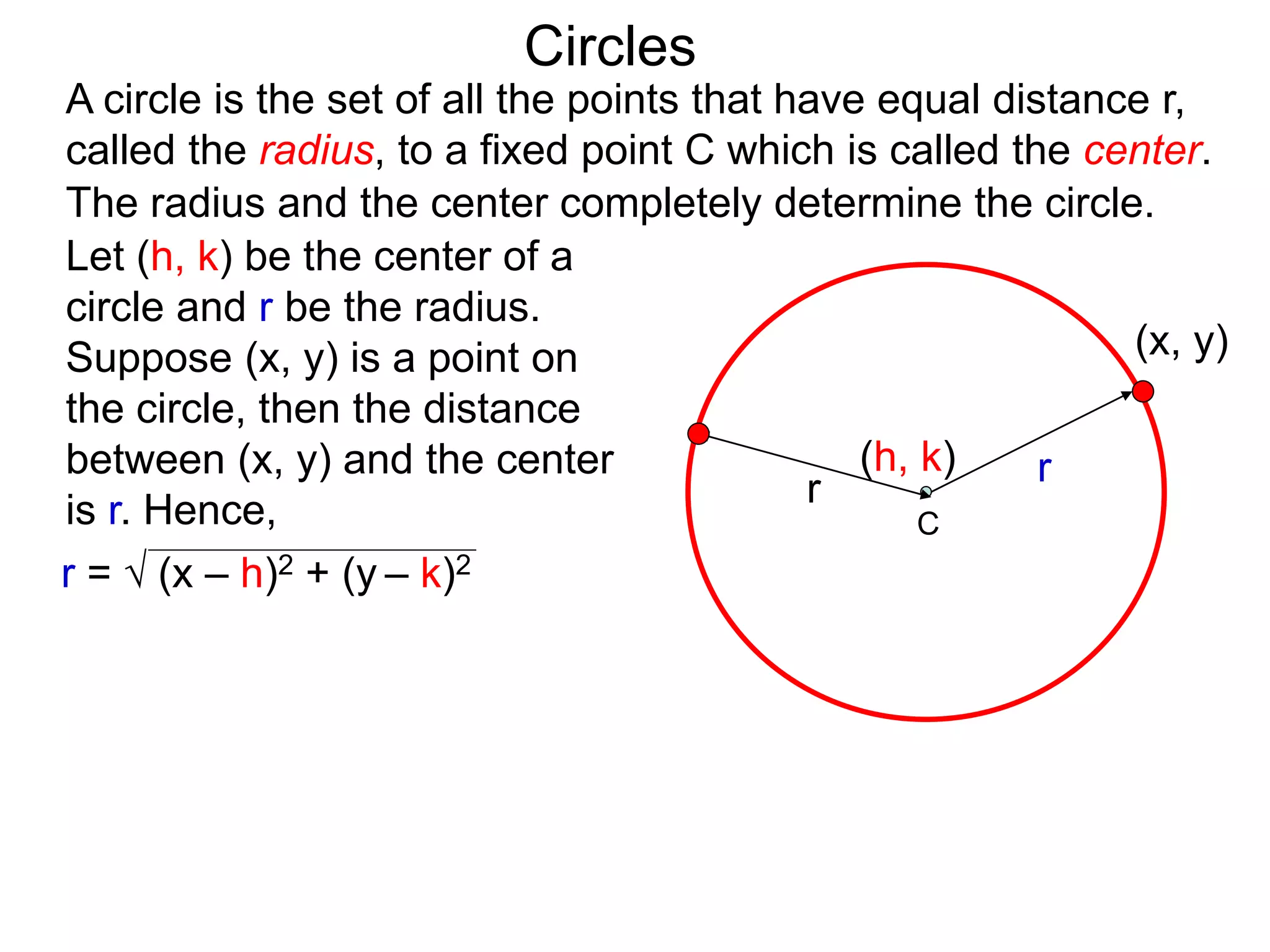
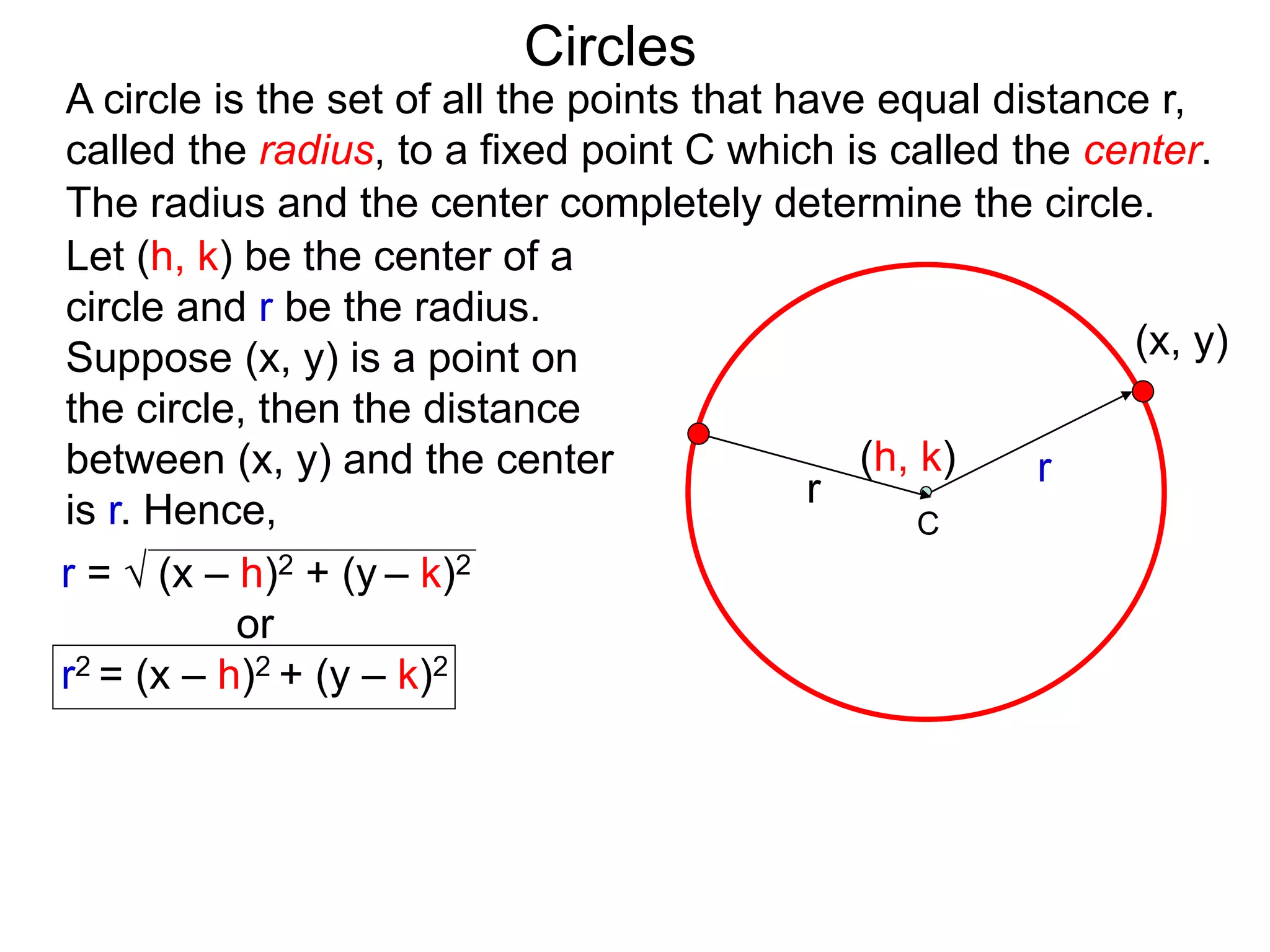
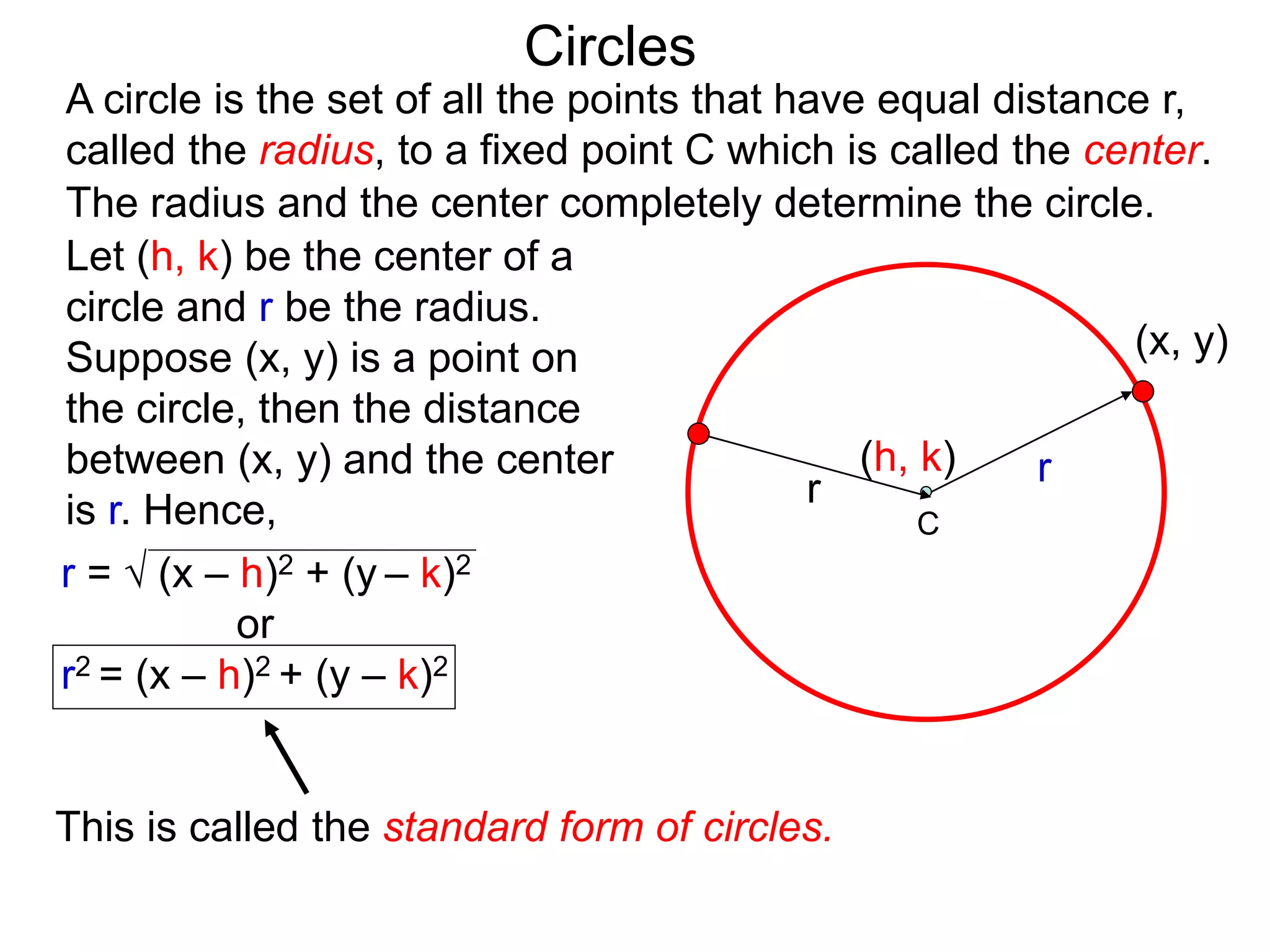
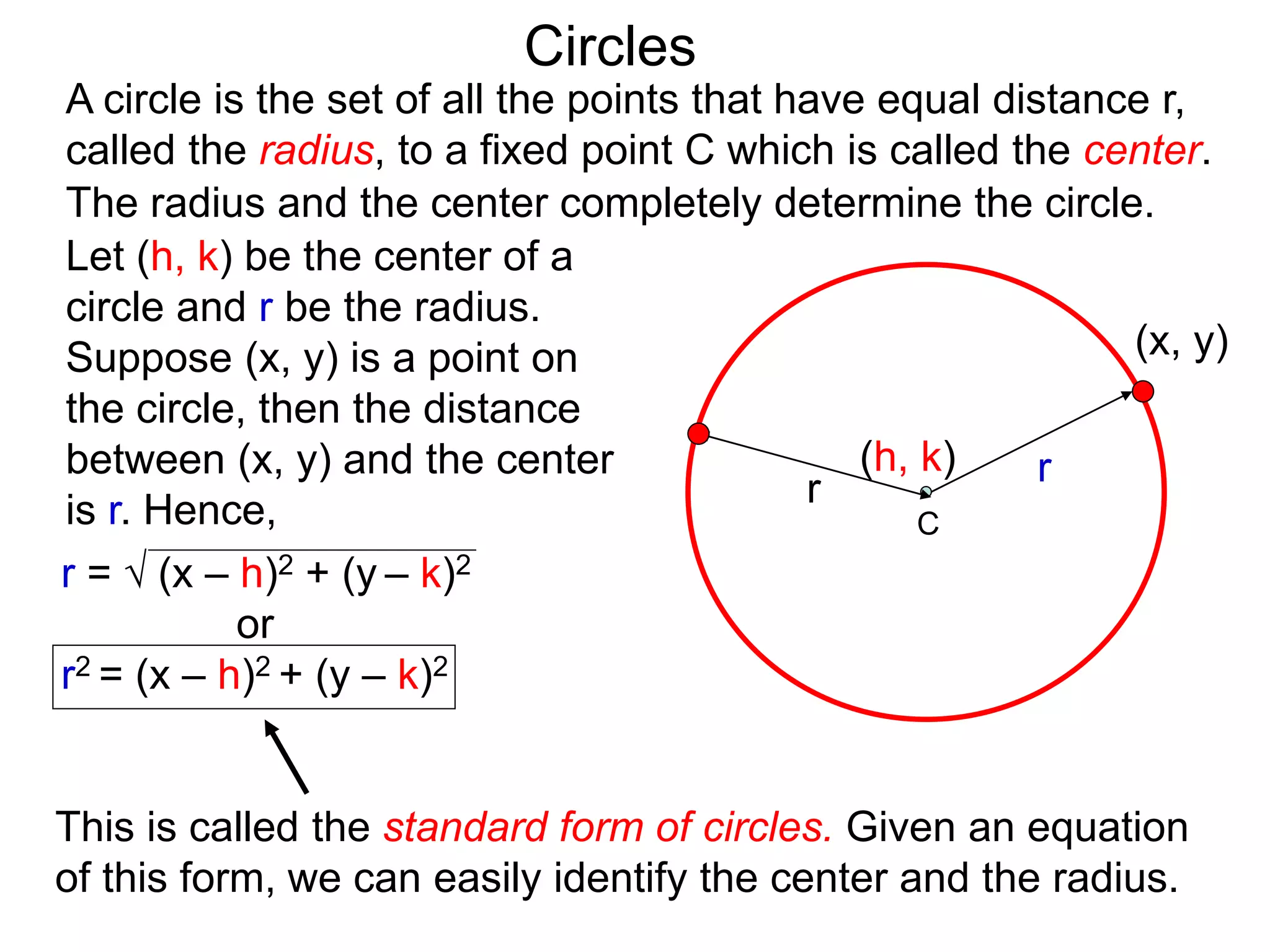
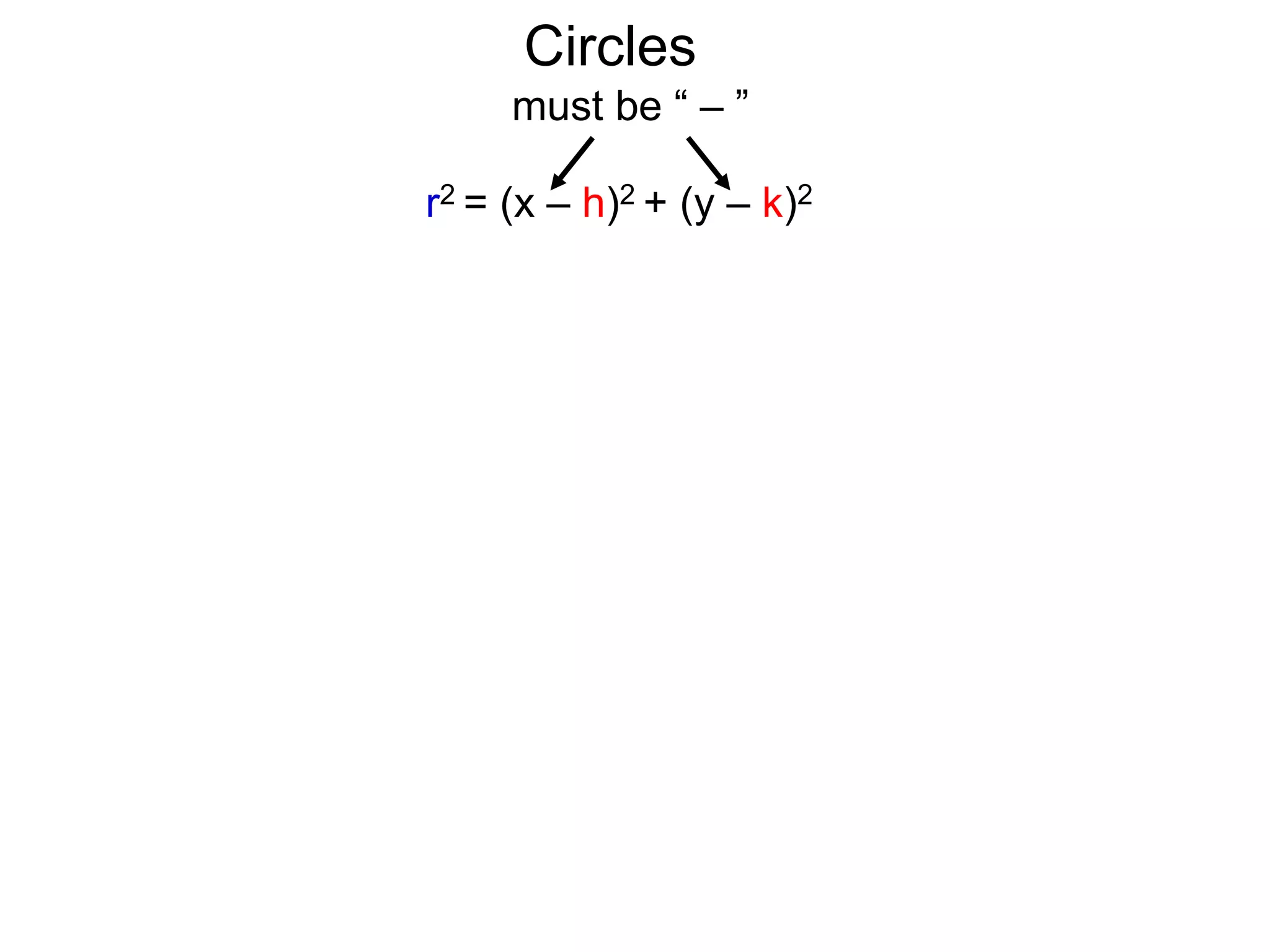
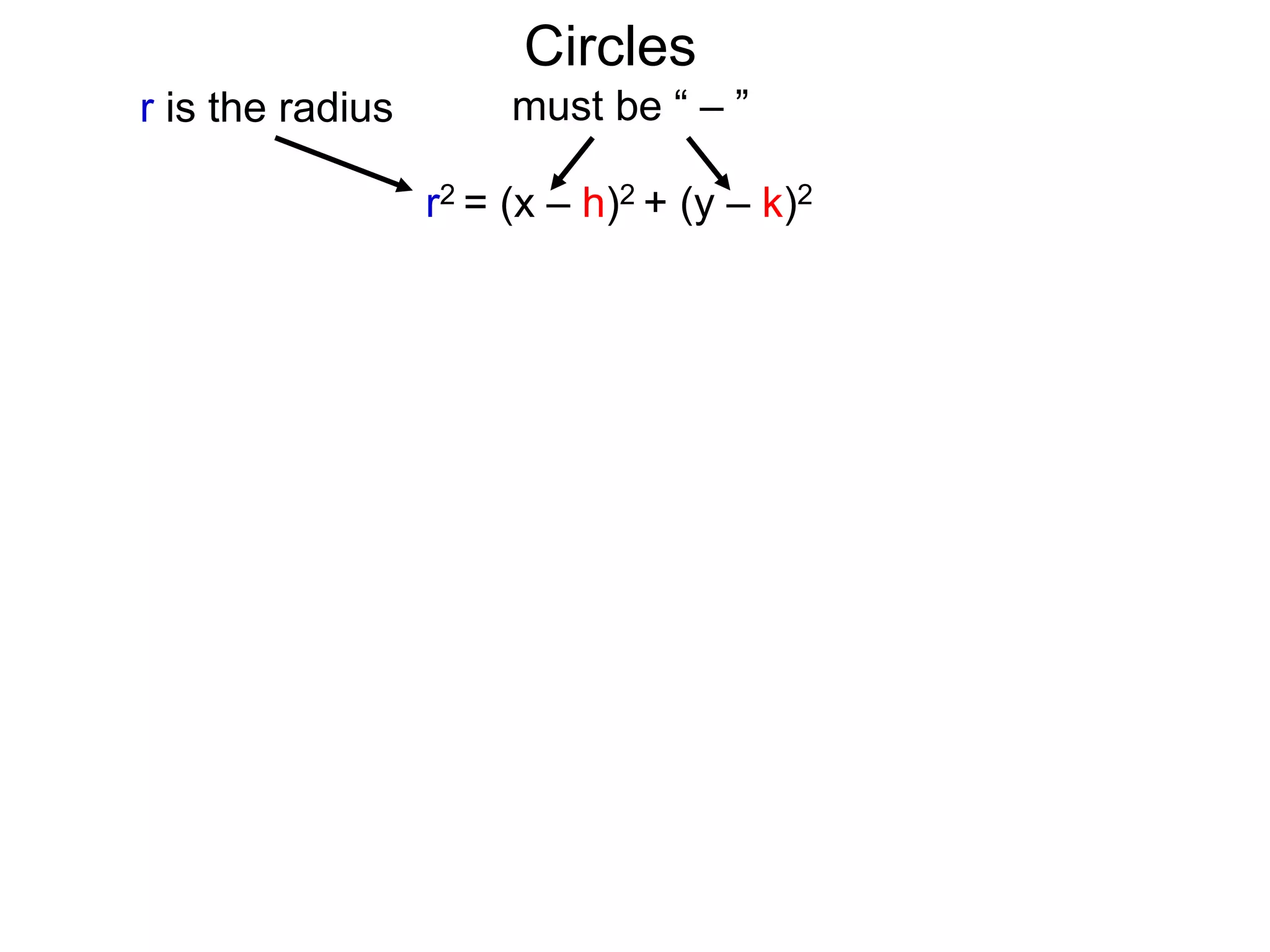
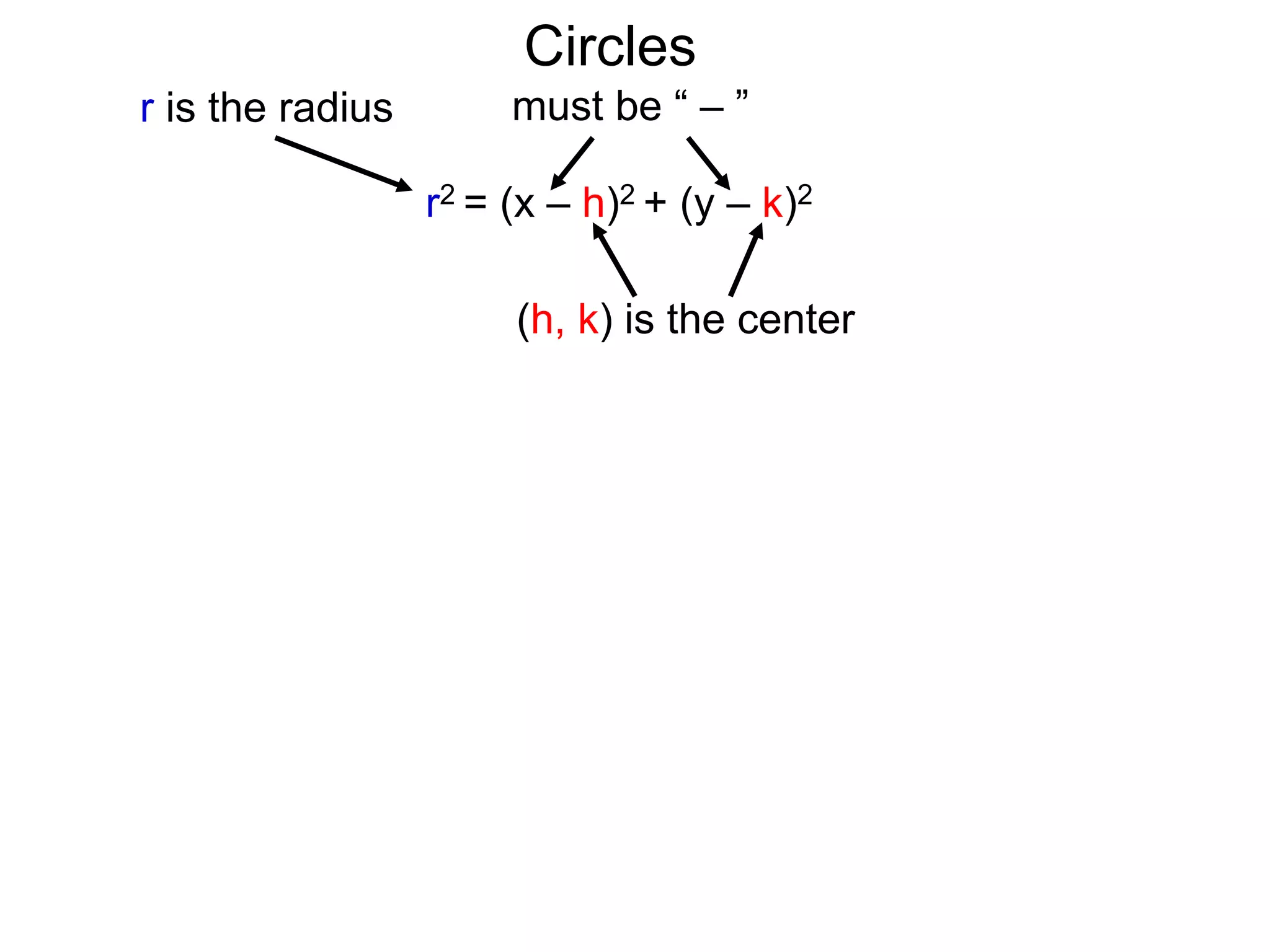
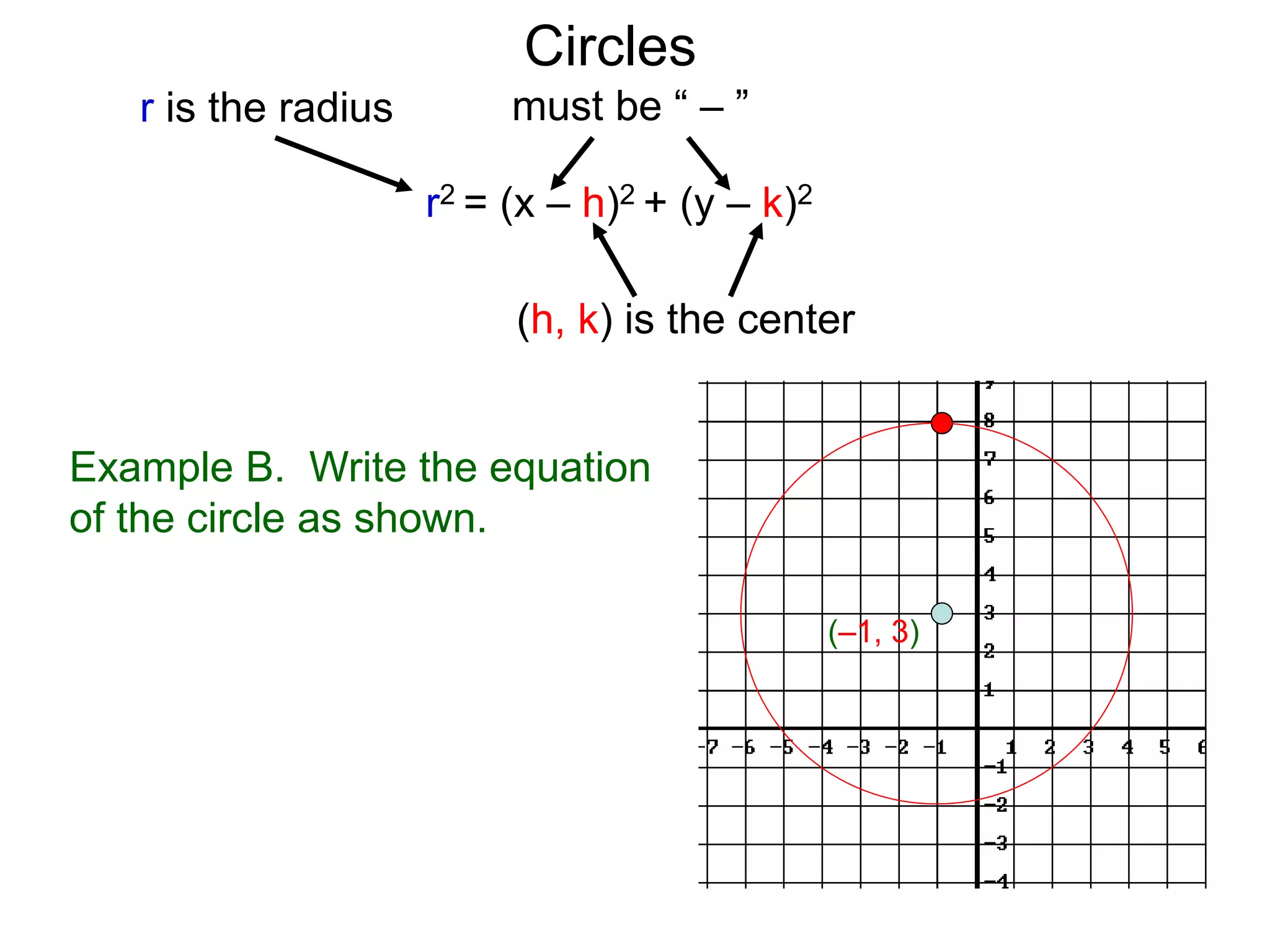
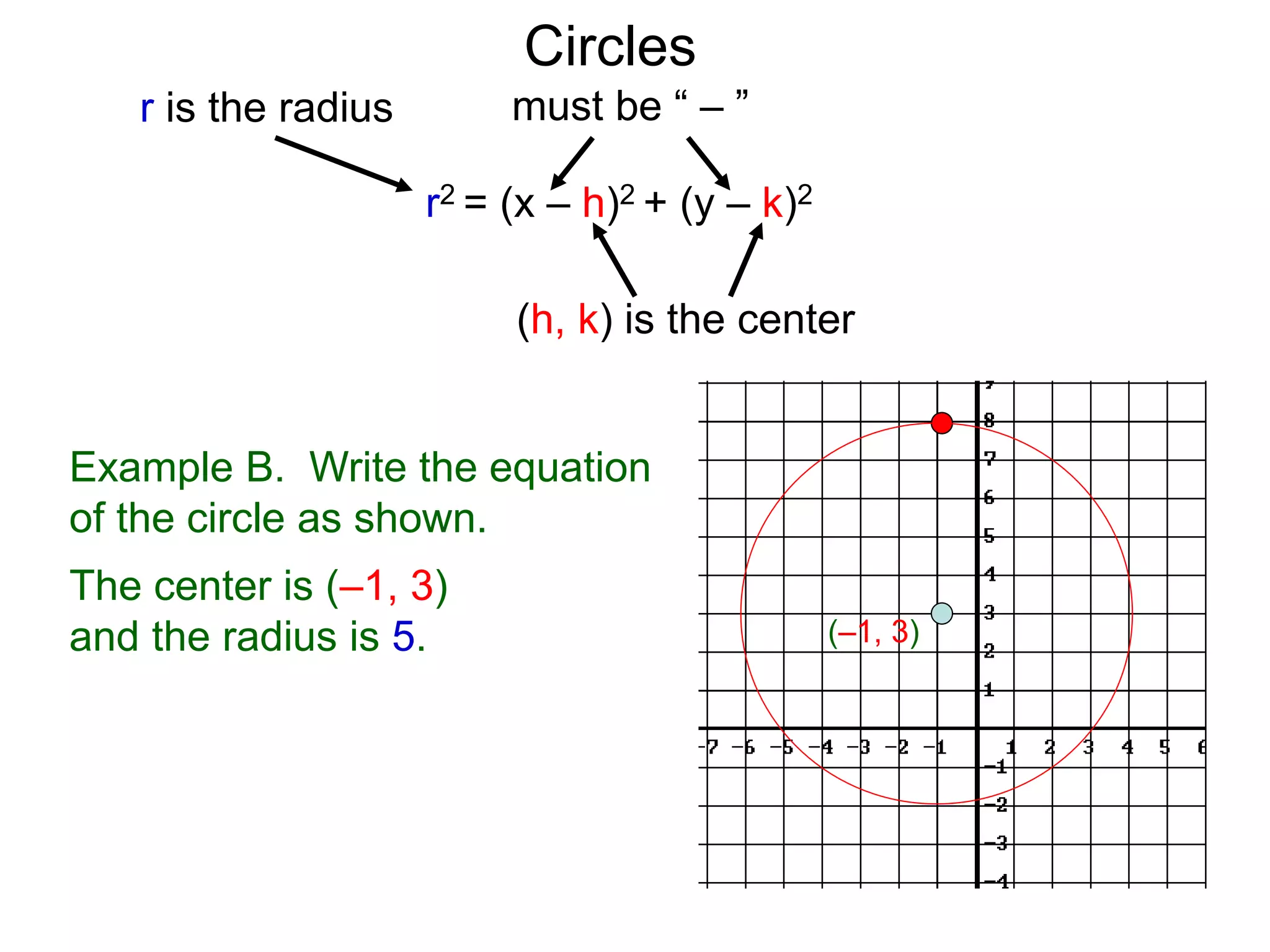
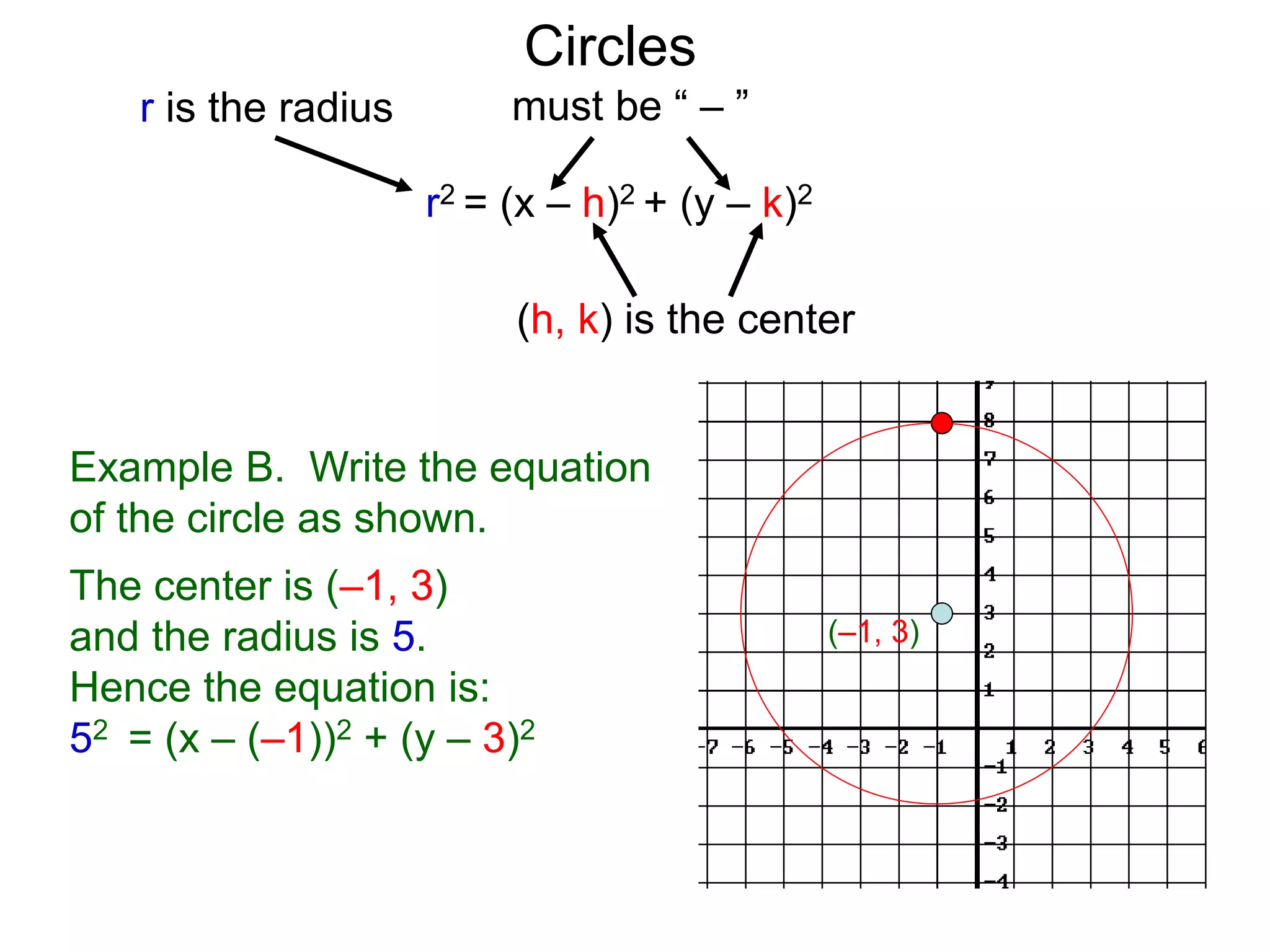
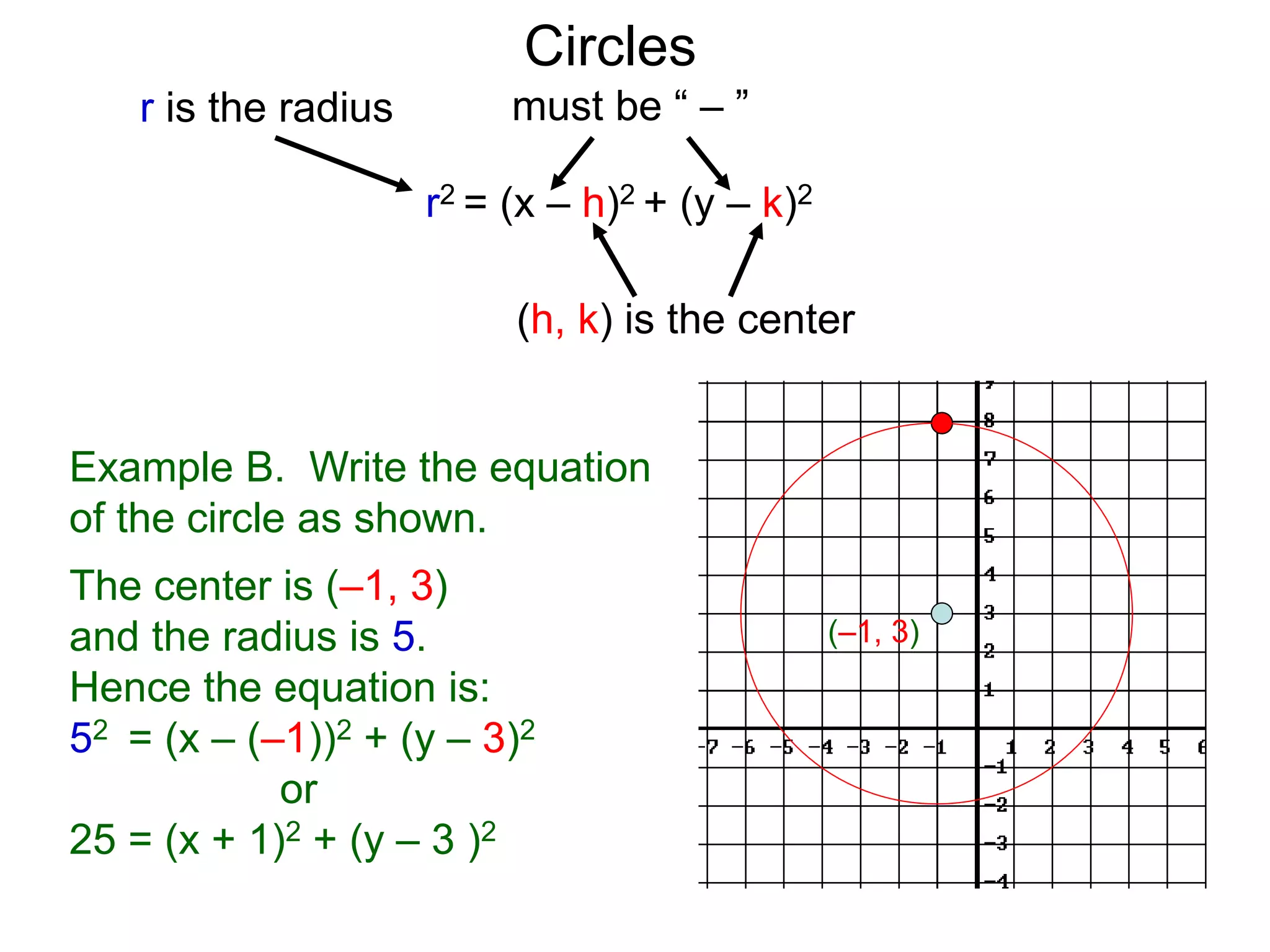
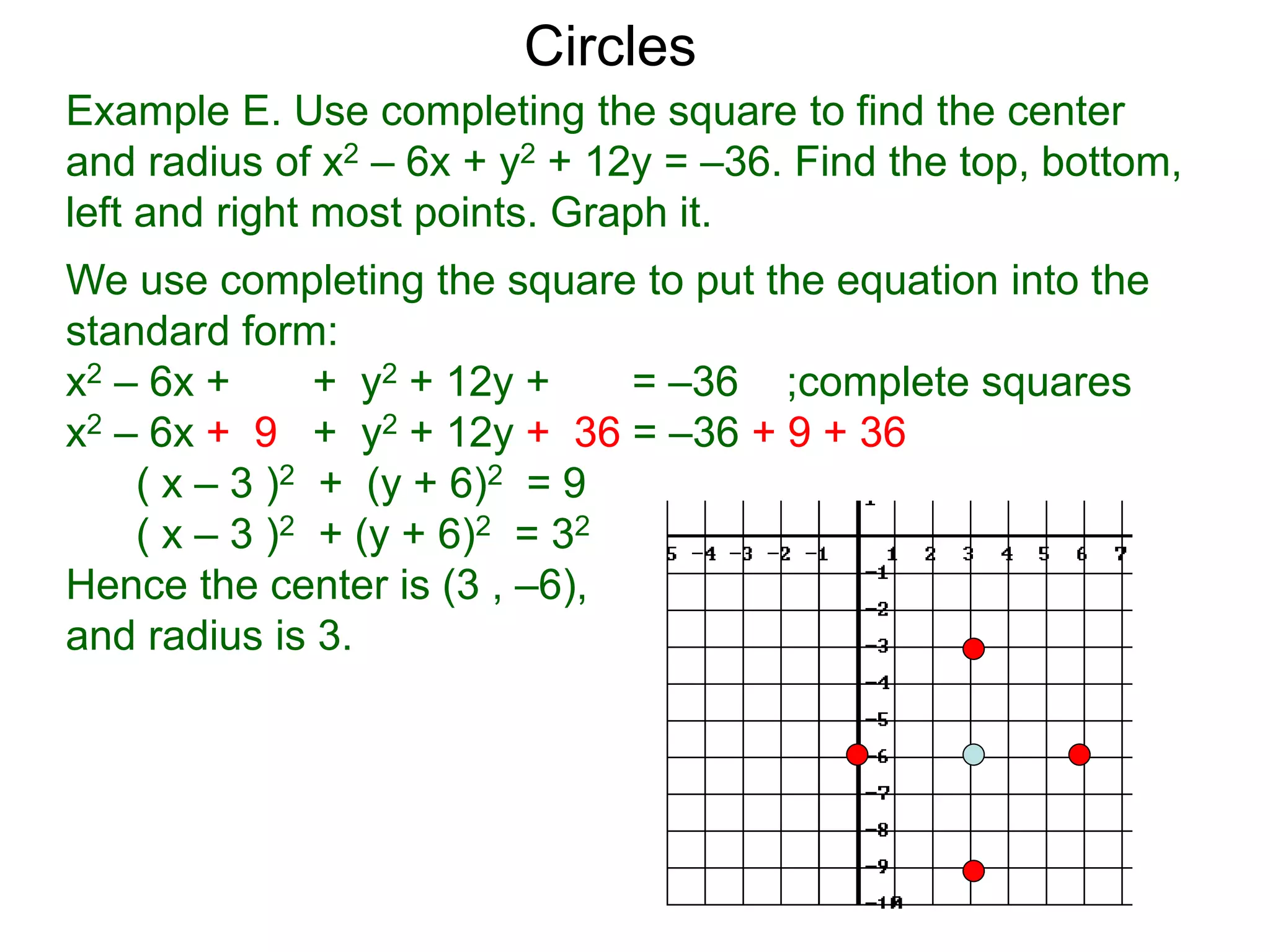
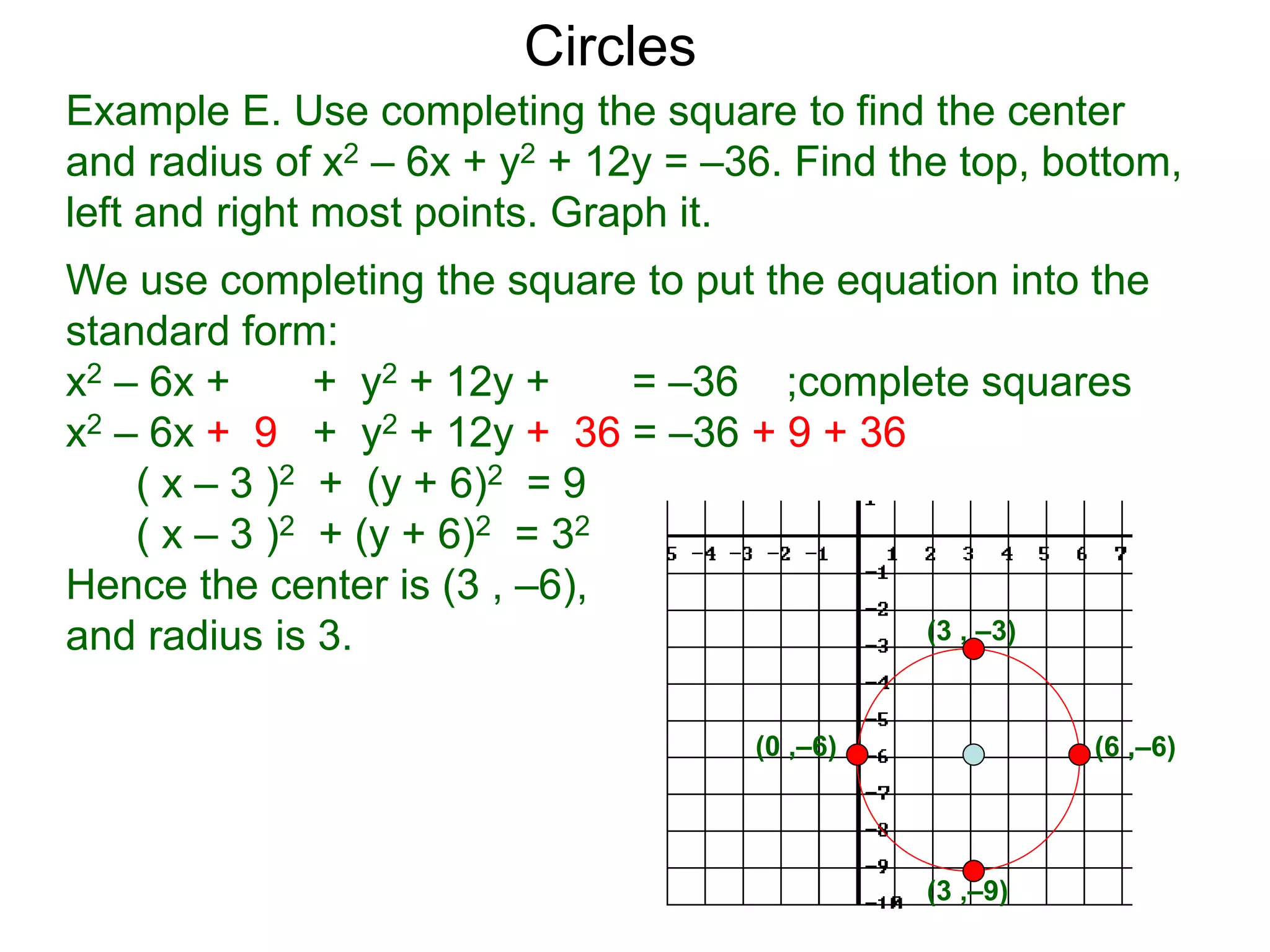
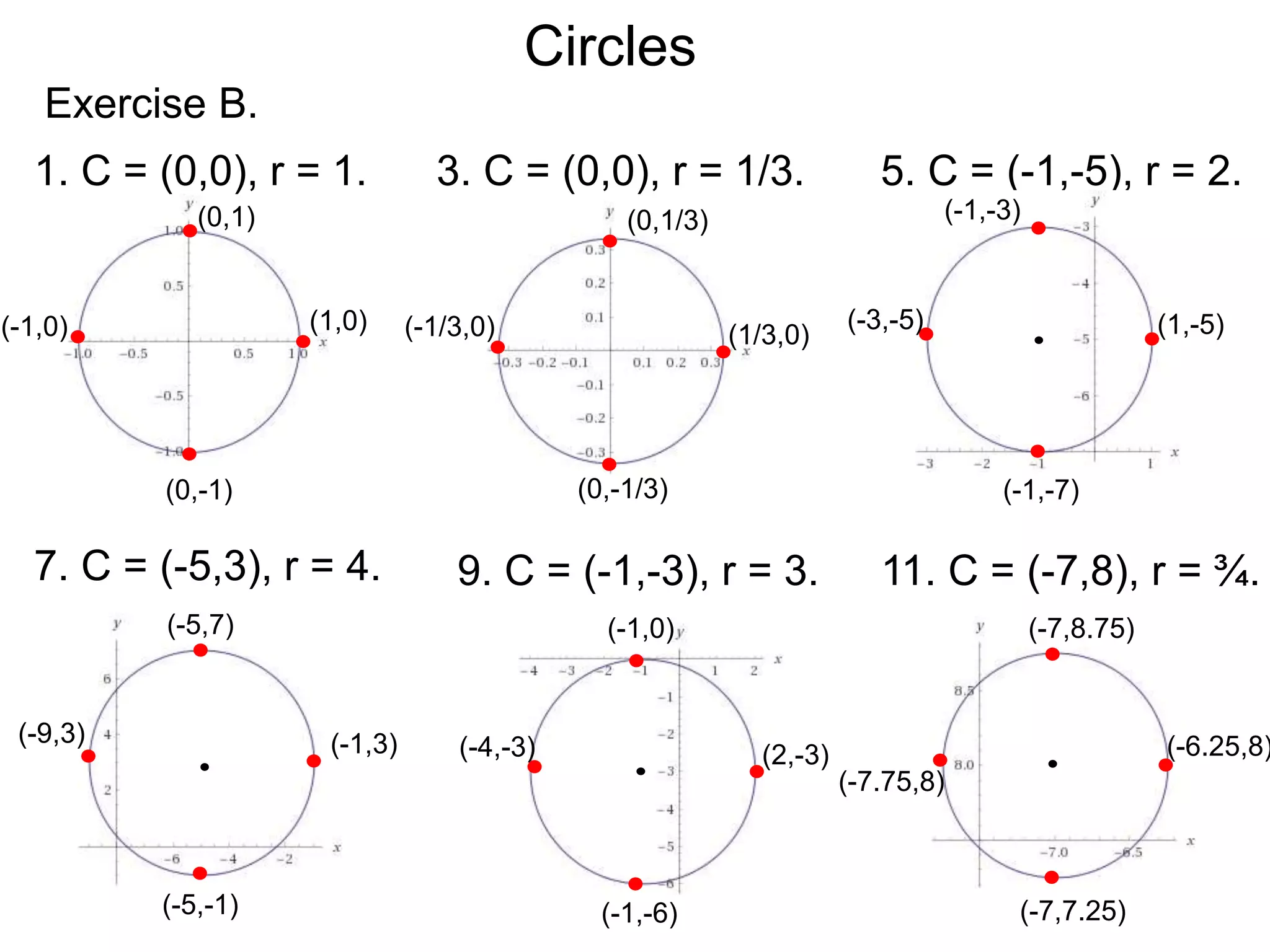
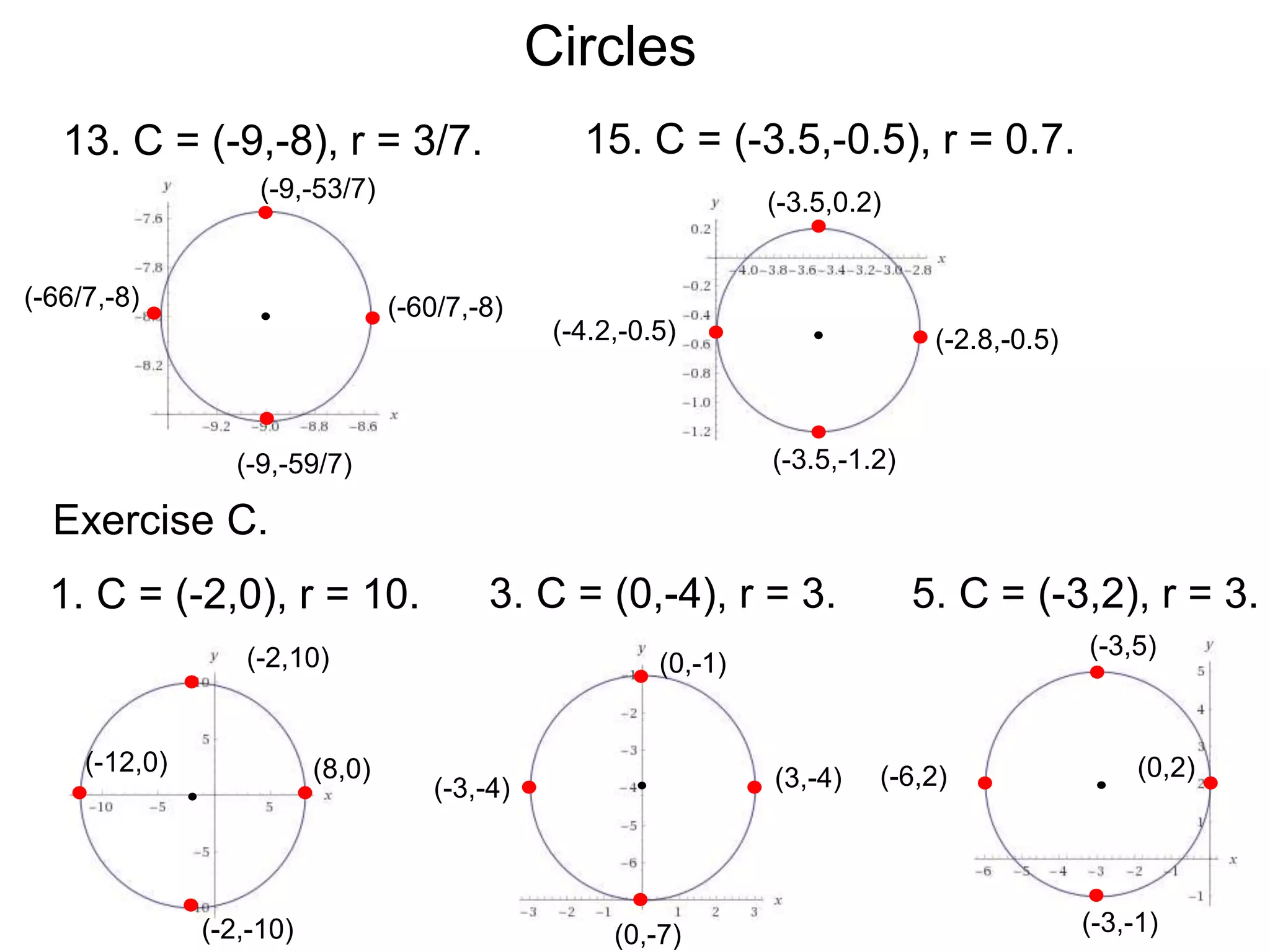
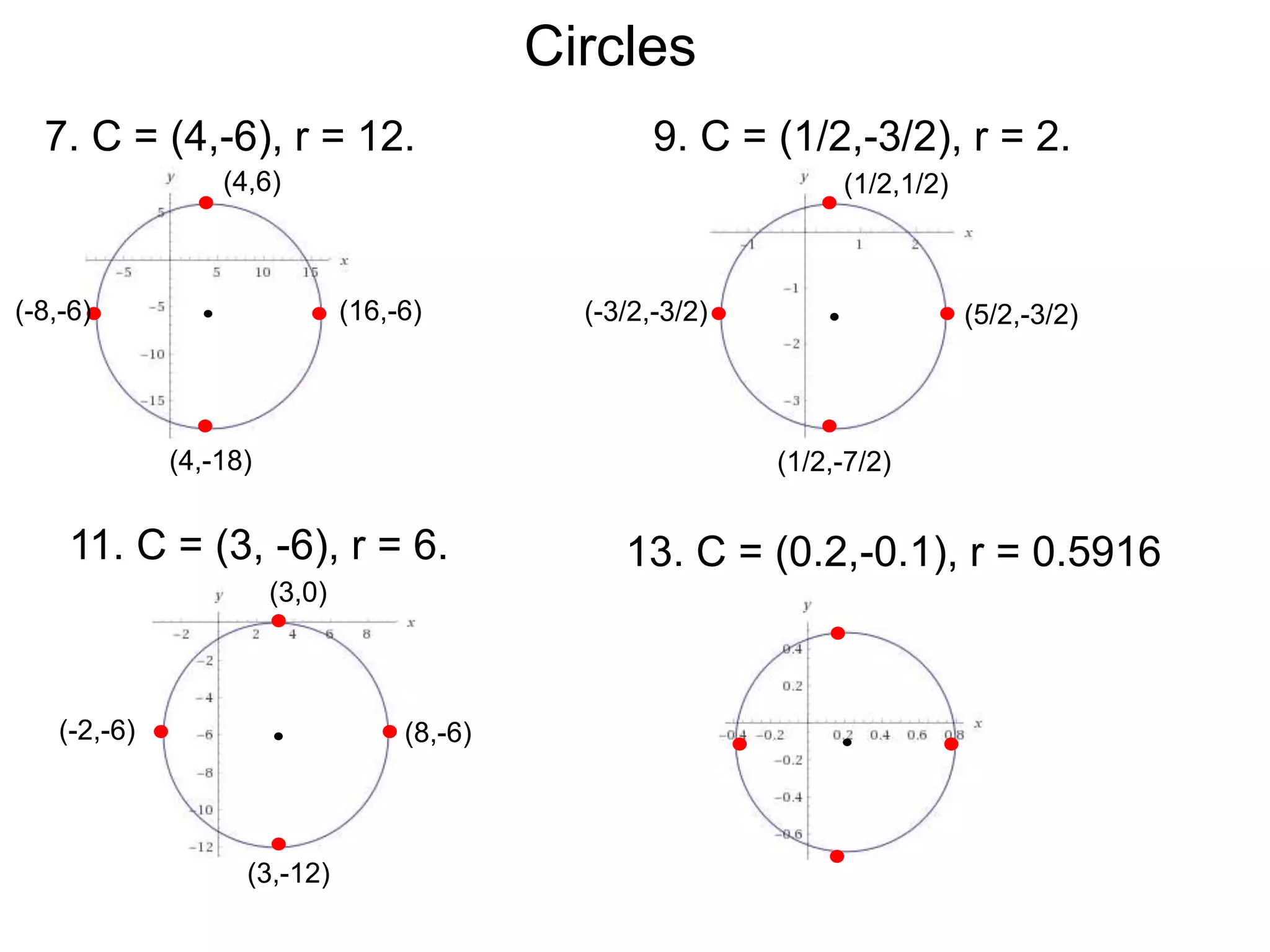
This document discusses conic sections and first degree equations. It begins by introducing conic sections as the shapes formed by slicing a cone at different angles. It then covers first degree equations, noting that their graphs are straight lines that can be written in the form of y=mx+b. Specific examples of first degree equations and their graphs are shown. The document ends by introducing the four types of conic sections - circles, ellipses, parabolas, and hyperbolas - and how graphs of second degree equations can represent these shapes.

1. Conic Sections
y2 + (x + ½)2 = ¼
(–1, 0)
Graph of equations
in x and y:
Graph of functions
y = f(x)
y = –x2
y = –x(x + 2)2(x – 3)2
y2 = x3 – 6x +4

2. Conic Sections

3. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines.

4. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.

5. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.

6. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
2x – 3y = 12

7. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
2x – 3y = 12
y = – 4
2 x
3

8. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4) 2x – 3y = 12
y = – 4
2 x
3

9. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4) 2x – 3y = 12
y = – 4
2 x
3

10. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3

11. First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3 (0,–4)

12. Graphs of
y = mx + b:
First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3 (0,–4)

13. Graphs of
y = mx + b:
First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3
Il. If B = 0, then the
equation is of the form x = c
whose graph is a vertical line.
12 – 3x = 0
(0,–4)

14. Graphs of
y = mx + b:
First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3
Il. If B = 0, then the
equation is of the form x = c
whose graph is a vertical line.
12 – 3x = 0
x = 4
(0,–4)

15. Graphs of
y = mx + b:
First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3
Il. If B = 0, then the
equation is of the form x = c
whose graph is a vertical line.
12 – 3x = 0
x = 4
Graphs of x = c
vertical lines:
(0,–4)
(4,0)

16. Graphs of
y = mx + b:
First Degree Equations
Graphs of 1st degree equations Ax + By = C are straight
lines. There are two cases.
I. If B ≠ 0, then solving for y we obtain the format: y = mx + b,
where m = slope, and (0, b) in the y-intercept.
(6,0)
(0,–4)
–3y = 12
y = –4
2x – 3y = 12
y = – 4
2 x
3
Il. If B = 0, then the
equation is of the form x = c
whose graph is a vertical line.
12 – 3x = 0
x = 4
Graphs of x = c
vertical lines:
Graphs of 2nd degree equations: Ax2 + By2 + Cx + Dy = E,
(A, B, C, D, and E are numbers) are conic-sections.
(0,–4)
(4,0)

17. Conic Sections
One way to study a solid is to slice it open.

18. Conic Sections
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.

19. Conic Sections
A right circular cone
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.

20. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.

21. Conic Sections
A Horizontal Section
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.

22. Conic Sections
A Horizontal Section
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
Circles

23. Conic Sections
A Moderately
Tilted Section
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.

24. Conic Sections
A Moderately
Tilted Section
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
Ellipses

25. Conic Sections
A Horizontal Section
A Moderately
Tilted Section
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
Circles and
ellipses are
enclosed.

26. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
A Parallel–Section
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.

27. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
A Parallel–Section
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
Parabolas

28. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
An Cut–away
Section

29. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
An Cut–away
Section
Hyperbolas

30. Conic Sections
A right circular cone and conic sections (wikipedia “Conic Sections”)
An Cut–away
Section
One way to study a solid is to slice it open. The exposed area
of the sliced solid is called a cross sectional area.
Conic sections are the borders of the cross sectional areas of
a right circular cone as shown.
Parabolas and
hyperbolas are open.
A Horizontal Section
A Moderately
Tilted Section
Circles and
ellipses are
enclosed.
A Parallel–Section

31. Conic Sections
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

32. Conic Sections
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections.

33. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

34. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
Graphs of
Ax2 + By2 + Cx + Dy = E,

35. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
Graphs of
Ax2 + By2 + Cx + Dy = E,

36. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

37. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
x2 – y2 = 0
For example,
the graphs of:
x + y = 0
x – y = 0

38. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
x2 – y2 = 0
For example,
the graphs of:
x + y = 0
x – y = 0
x2 + y2 = 0
(0,0)
(0,0) is the
only solution

39. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.
x2 – y2 = 0
For example,
the graphs of:
x + y = 0
x – y = 0
x2 = –1
x2 + y2 = 0
(0,0)
(0,0) is the
only solution
No solution
no graph

40. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
We will match these 2nd degree equations with different conic
sections using the algebraic method "completing the square".
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

41. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
We will match these 2nd degree equations with different conic
sections using the algebraic method "completing the square".
“Completing the Square“ is THE main algebraic algorithm
for handling all 2nd degree formulas.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

42. Conic Sections
(Most) Graphs of 2nd equations Ax2 + By2 + Cx + Dy = E,
are conic sections. The equations Ax2 + By2 + Cx + Dy = E
have conic sections that are parallel to the axes, i.e. not tilted,
as graphs. In some special cases their graphs degenerate into
lines or points, or nothing.
We will match these 2nd degree equations with different conic
sections using the algebraic method "completing the square".
“Completing the Square“ is THE main algebraic algorithm
for handling all 2nd degree formulas.
We need the Distance Formula D = Δx2 + Δy2 for the geometry.
Circles Ellipses Parabolas Hyperbolas
We summarize the four types of conic sections here.

43. Circles
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.

44. Circles
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
C

45. r
r
Circles
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
C

46. r
r
Circles
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
C

47. r
r
The radius and the center completely determine the circle.
Circles
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
C

48. r
The radius and the center completely determine the circle.
Circles
Let (h, k) be the center of a
circle and r be the radius.
(h, k)
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

49. r
The radius and the center completely determine the circle.
Circles
(x, y)
Let (h, k) be the center of a
circle and r be the radius.
Suppose (x, y) is a point on
the circle, then the distance
between (x, y) and the center
is r.
(h, k)
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

50. r
The radius and the center completely determine the circle.
Circles
(x, y)
Let (h, k) be the center of a
circle and r be the radius.
Suppose (x, y) is a point on
the circle, then the distance
between (x, y) and the center
is r. Hence,
(h, k)
r =  (x – h)2 + (y – k)2
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

51. r
The radius and the center completely determine the circle.
Circles
(x, y)
Let (h, k) be the center of a
circle and r be the radius.
Suppose (x, y) is a point on
the circle, then the distance
between (x, y) and the center
is r. Hence,
(h, k)
r =  (x – h)2 + (y – k)2
or
r2 = (x – h)2 + (y – k)2
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

52. r
The radius and the center completely determine the circle.
Circles
(x, y)
Let (h, k) be the center of a
circle and r be the radius.
Suppose (x, y) is a point on
the circle, then the distance
between (x, y) and the center
is r. Hence,
(h, k)
r =  (x – h)2 + (y – k)2
or
r2 = (x – h)2 + (y – k)2
This is called the standard form of circles.
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

53. r
The radius and the center completely determine the circle.
Circles
(x, y)
Let (h, k) be the center of a
circle and r be the radius.
Suppose (x, y) is a point on
the circle, then the distance
between (x, y) and the center
is r. Hence,
(h, k)
r =  (x – h)2 + (y – k)2
or
r2 = (x – h)2 + (y – k)2
This is called the standard form of circles. Given an equation
of this form, we can easily identify the center and the radius.
A circle is the set of all the points that have equal distance r,
called the radius, to a fixed point C which is called the center.
r
C

54. r2 = (x – h)2 + (y – k)2
Circles

55. r2 = (x – h)2 + (y – k)2
must be “ – ”
Circles

56. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
Circles

57. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
(h, k) is the center
Circles

58. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
(h, k) is the center
Circles
Example B. Write the equation
of the circle as shown.
(–1, 3)

59. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
(h, k) is the center
Circles
Example B. Write the equation
of the circle as shown.
The center is (–1, 3)
and the radius is 5. (–1, 3)

60. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
(h, k) is the center
Circles
Example B. Write the equation
of the circle as shown.
The center is (–1, 3)
and the radius is 5.
Hence the equation is:
52 = (x – (–1))2 + (y – 3)2
(–1, 3)

61. r2 = (x – h)2 + (y – k)2
r is the radius must be “ – ”
(h, k) is the center
Circles
Example B. Write the equation
of the circle as shown.
The center is (–1, 3)
and the radius is 5.
Hence the equation is:
52 = (x – (–1))2 + (y – 3)2
or
25 = (x + 1)2 + (y – 3 )2
(–1, 3)

62. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Circles

63. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Circles

64. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
Circles

65. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
(3,–2)
Circles
r = 4

66. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
(3,–2)
Circles
r = 4

67. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
(3,–2)
Circles
When equations are not in the standard form, we have to
rearrange them into the standard form. We do this by
"completing the square".
r = 4

68. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
(3,–2)
Circles
When equations are not in the standard form, we have to
rearrange them into the standard form. We do this by
"completing the square".
To complete the square means to add a number to an
expression so the sum is a perfect square.
r = 4

69. Example C. Identify the center and
the radius of 16 = (x – 3)2 + (y + 2)2.
Label the top, bottom, left and right
most points. Graph it.
Put 16 = (x – 3)2 + (y + 2)2 into the
standard form:
42 = (x – 3)2 + (y – (–2))2
Hence r = 4, center = (3, –2)
(3,–2)
Circles
When equations are not in the standard form, we have to
rearrange them into the standard form. We do this by
"completing the square".
To complete the square means to add a number to an
expression so the sum is a perfect square. This procedure is
the main technique in dealing with 2nd degree equations.
r = 4

70. (Completing the Square)
Circles

71. (Completing the Square)
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

72. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square,
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

73. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square,
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

74. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square,
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

75. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

76. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2

77. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2

78. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36

79. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2

80. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2
The following are the steps in putting a 2nd degree equation
into the standard form.

81. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2
The following are the steps in putting a 2nd degree equation
into the standard form.
1. Group the x2 and the x–terms together, group the y2 and y
terms together, and move the number term the the other
side of the equation.

82. (Completing the Square)
If we are given x2 + bx, then adding (b/2)2 to the expression
makes the expression a perfect square, i.e. x2 + bx + (b/2)2
is the perfect square (x + b/2)2.
Circles
Example D. Fill in the blank to make a perfect square.
a. x2 – 6x + (–6/2)2 = x2 – 6x + 9 = (x – 3)2
b. y2 + 12y + (12/2)2 = y2 + 12y + 36 = ( y + 6)2
The following are the steps in putting a 2nd degree equation
into the standard form.
1. Group the x2 and the x–terms together, group the y2 and y
terms together, and move the number term the the other
side of the equation.
2. Complete the square for the x–terms and for the y–terms.
Make sure you add the necessary numbers to both sides.

83. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
Circles

84. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
Circles

85. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36
Circles

86. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
Circles

87. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
Circles

88. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
Circles

89. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
( x – 3 )2 + (y + 6)2 = 32
Circles

90. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
( x – 3 )2 + (y + 6)2 = 32
Hence the center is (3 , –6),
and radius is 3.
Circles

91. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
( x – 3 )2 + (y + 6)2 = 32
Hence the center is (3 , –6),
and radius is 3.
Circles

92. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
( x – 3 )2 + (y + 6)2 = 32
Hence the center is (3 , –6),
and radius is 3.
Circles

93. Example E. Use completing the square to find the center
and radius of x2 – 6x + y2 + 12y = –36. Find the top, bottom,
left and right most points. Graph it.
We use completing the square to put the equation into the
standard form:
x2 – 6x + + y2 + 12y + = –36 ;complete squares
x2 – 6x + 9 + y2 + 12y + 36 = –36 + 9 + 36
( x – 3 )2 + (y + 6)2 = 9
( x – 3 )2 + (y + 6)2 = 32
Hence the center is (3 , –6),
and radius is 3.
Circles
(3 ,–9)
(3 , –3)
(0 ,–6) (6 ,–6)

94. Conic Sections

95. Circles
B. Find the radius and the center of each circle.
Draw and label the four cardinal points.
1 = x 2 + y 2
1. 4 = x 2 + y 2
2.
1 = (x – 1)2 + (y – 3 )2
4. 4 = (x + 1)2 + (y + 5)2
5.
1/9 = x2 + y2
3.
1/4 = (x – 2)2 + (y + 3/2)2
6. 16 = (x + 5)2 + (y – 3)2
7.
25 = (x + 5)2 + (y – 4)2
8. 9 = (x + 1)2 + (y + 3)2
9.
1/16 = (x – 4)2 + (y – 6)2
10. 9/16 = (x + 7)2 + (y – 8)2
11.
1/100 = (x + 1.2)2 + (y – 4.1)2
12. 9/49 = (x + 9)2 + (y + 8)2
13.
0.01 = (x – 1.5 )2 + (y + 3.5)2
14.
0.49 = (x + 3.5)2 + (y + 0.5)2
15.

96. 2.
C. Complete the square to find the center and radius of each
of the following circles. Draw and label the four cardinal points.
1.
4.
3.
6.
5.
8.
7.
13.
14.
Approximate the radius In the following problems.
x2 + y2 – 2y = 35
x2 – 8x + y2 + 12y = 92
x2 – 4y + y2 + 6x = –4
y2 – 8x + x2 + 2y = 8
x2 + 18y + y2 – 8x = 3
2x2 – 8x + 2y2 +12y = 1
x2 – 6x + y2 + 12y = –9
x2 + y2 + 8y = –7
x2 + 4x + y2 = 96
Circles
x2 + 6y + y2 – 16x = –9
10.
9. x2 – x + y2 + 3y = 3/2 x2 + 3y + y2 – 5x = 1/2
12.
11.
x2 – 0.4x + y2 + 0.2y = 0.3
x2 + 0.8y + y2 – 1.1x = –0.04

97. 1. The circle that has (3,1) and (1,3) as its diameter.
D. Use the midpoint formula and the distance formula to find
the center and the radius of each circle.
Then find the equation of each circle.
Circles
2. The circle that has (–2,4) and (0,–3) as its diameter.
3.
4. The circle that has (6, –3) and (0,–3) as its diameter.
The circle that has (5,–4) and (–2,–1) as its diameter.

98. (Answers to odd problems) Ex. A
1. x2 + y2 = 25 5. (x – 1)2 + y2 = 9
3. x2 + y2 = 5
7. (x – 1)2 + (y + 1)2 = 81 9. (x + 3)2 + (y + 2)2 = 16
Circles
(0,5)
(0,-5)
(5,0)
(-5,0)
(0,√5)
(0,-√5)
(√5,0)
(-√5,0)
(1,3)
(1,-3)
(4,0)
(-2,0)
(1,8)
(1,-10)
(10,0)
(-8,0)
(-3,2)
(-3,-6)
(1,-2)
(-2,-2)

99. Exercise B.
1. C = (0,0), r = 1. 5. C = (-1,-5), r = 2.
3. C = (0,0), r = 1/3.
7. C = (-5,3), r = 4. 9. C = (-1,-3), r = 3. 11. C = (-7,8), r = ¾.
Circles
(0,1)
(0,-1)
(1,0)
(-1,0)
(0,1/3)
(0,-1/3)
(1/3,0)
(-1/3,0)
(-1,-3)
(-1,-7)
(1,-5)
(-3,-5)
(-5,7)
(-5,-1)
(-1,3)
(-9,3)
(-1,0)
(-1,-6)
(2,-3)
(-4,-3)
(-7,8.75)
(-7,7.25)
(-6.25,8)
(-7.75,8)

100. 13. C = (-9,-8), r = 3/7. 15. C = (-3.5,-0.5), r = 0.7.
Exercise C.
5. C = (-3,2), r = 3.
3. C = (0,-4), r = 3.
1. C = (-2,0), r = 10.
Circles
(-9,-53/7)
(-9,-59/7)
(-60/7,-8)
(-66/7,-8)
(-3.5,0.2)
(-3.5,-1.2)
(-2.8,-0.5)
(-4.2,-0.5)
(-2,10)
(-2,-10)
(8,0)
(-12,0)
(0,-1)
(0,-7)
(3,-4)
(-3,-4)
(-3,5)
(-3,-1)
(0,2)
(-6,2)

101. 7. C = (4,-6), r = 12. 9. C = (1/2,-3/2), r = 2.
13. C = (0.2,-0.1), r = 0.5916
11. C = (3, -6), r = 6.
Circles
(3,0)
(3,-12)
(8,-6)
(-2,-6)
(1/2,1/2)
(1/2,-7/2)
(5/2,-3/2)
(-3/2,-3/2)
(4,6)
(4,-18)
(16,-6)
(-8,-6)

102. 1. C = (2, 2), r = √2.
Equation: (x – 2)2 + (y – 2)2 = 2
Exercise D.
3. C = (3/2, -5/2), r = (√58)/2.
Equation: (x – 3/2)2 + (y + 5/2)2 = 14.5
Circles