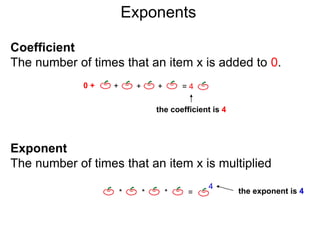
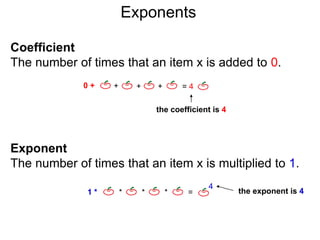
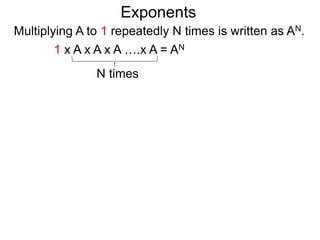
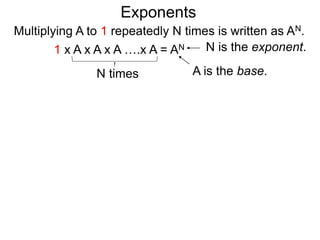
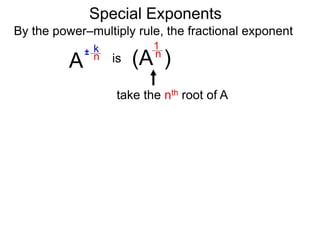
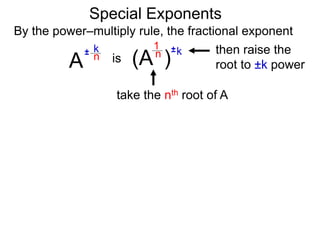
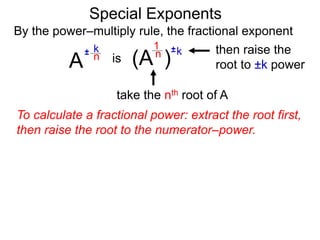
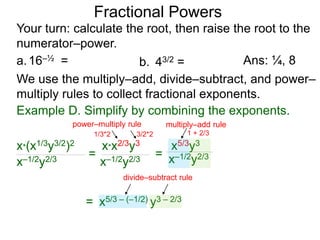
The document discusses exponents and exponent rules. It defines exponents as the number of times a base is multiplied by 1. It presents rules for multiplying, dividing, and raising exponents. Examples are provided to demonstrate applying the rules, such as using the power-multiply rule to evaluate (22*34)3. Special exponent rules are also covered, such as the 0-power rule where A0 equals 1 when A is not 0. The document provides examples of calculating fractional exponents by first extracting the root and then raising it to the numerator power.

1. Exponents
Math 260
Dr. Frank Ma
LA Harbor College

2. Exponents
Coefficient
The number of times that an item x is added to 0.
+ = 4
+
+
the coefficient is 4
0 +

3. Exponents
Coefficient
The number of times that an item x is added to 0.
Exponent
The number of times that an item x is multiplied to 1.
+ = 4
+
+
the coefficient is 4
0 +
1 * * * * =
4
the exponent is 4
Math 260
Dr. Frank Ma
LA Harbor College

4. Exponents
Coefficient
The number of times that an item x is added to 0.
Exponent
The number of times that an item x is multiplied to 1.
+ = 4
+
+
the coefficient is 4
0 +
1 * * * * =
4
the exponent is 4

5. Exponents
Coefficient
The number of times that an item x is added to 0.
Exponent
The number of times that an item x is multiplied to 1.
+ = 4
+
+
the coefficient is 4
0 +
1 * * * * =
4
the exponent is 4

6. Exponents
Multiplying A to 1 repeatedly N times is written as AN.

7. Exponents
Multiplying A to 1 repeatedly N times is written as AN.
N times
1 x A x A x A ….x A = AN

8. Exponents
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

9. Multiply–Add Rule:
Divide–Subtract Rule:
Power–Multiply Rule:
Exponents
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

10. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Power–Multiply Rule:
Exponents
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

11. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 =
Power–Multiply Rule:
Exponents
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

12. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5)
Power–Multiply Rule:
Exponents
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

13. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
Power–Multiply Rule:
Exponents
(multiply–add)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

14. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
Power–Multiply Rule:
Exponents
= An – k
(multiply–add)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

15. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. =
55
52
Power–Multiply Rule:
Exponents
= An – k
(multiply–add)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

16. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule:
Exponents
= An – k
(multiply–add)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

17. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule:
Exponents
= An – k
(multiply–add)
(divide–subtract)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

18. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule: (An)k = Ank , (An Bm)k = Ank Bmk
Exponents
= An – k
(multiply–add)
(divide–subtract)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

19. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule: (An)k = Ank , (An Bm)k = Ank Bmk
c. (22*34)3 =
Exponents
= An – k
(multiply–add)
(divide–subtract)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

20. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule: (An)k = Ank , (An Bm)k = Ank Bmk
c. (22*34)3 = 26*312
Exponents
= An – k
(multiply–add)
(divide–subtract)
(power–multiply)
Exponent–Rules
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

21. Multiply–Add Rule: AnAk = An+k
Divide–Subtract Rule:
Example A.
a. 5254 = (5*5)(5*5*5*5) = 52 + 4 = 56
An
Ak
b. = 55–2 = 53
55
52
Power–Multiply Rule: (An)k = Ank , (An Bm)k = Ank Bmk
c. (22*34)3 = 26*312
Exponents
= An – k
(multiply–add)
(divide–subtract)
(power–multiply)
Exponent–Rules
! Note that
(22 ± 34)3 = 26 ± 38
Multiplying A to 1 repeatedly N times is written as AN.
A is the base.
N is the exponent.
N times
1 x A x A x A ….x A = AN

22. 0-power Rule: A0 = 1 (A≠0)
Special Exponents

23. 0-power Rule: A0 = 1 (A=0)
Special Exponents
because 1 = A1
A1

24. 0-power Rule: A0 = 1 (A=0)
Special Exponents
because 1 = = A1–1 = A0
A1
A1
(divide–subtract)

25. 0-power Rule: A0 = 1 (A=0)
Special Exponents
because 1 = = A1–1 = A0
A1
A1
(divide–subtract)

26. 0-power Rule: A0 = 1 (A=0)
1
Ak
Special Exponents
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
(divide–subtract)

27. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because
(divide–subtract)

28. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

29. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

30. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2,
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

31. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
(divide–subtract)
(divide–subtract)

32. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
(divide–subtract)
(divide–subtract)

33. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 =
a. 641/2 =
(divide–subtract)
(divide–subtract)

34. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 =
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

35. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 =
b. 81/3 = 8 = 2
3
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

36. 0-power Rule: A0 = 1 (A=0)
=
1
Ak
1
Ak
A0
Ak
Special Exponents
½ - Power Rule: A½ = A , the square root of A,
because (A½)2 = A = (A)2, so A½ = A
Example B.
because 1 = = A1–1 = A0
A1
A1
Negative Power Rule: A–k =
because = A0–k = A–k
1/n - Power Rule: A1/n = A , the nth root of A.
n
c. 641/3 = 64 = 4
3
b. 81/3 = 8 = 2
3
a. 641/2 = 64 = 8
(divide–subtract)
(divide–subtract)

37. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n
±

38. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n
±
(A )
n
1
is
take the nth root of A

39. Special Exponents
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power

40. Special Exponents
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power

41. Special Exponents
a. 9 –3/2 =
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

42. Special Exponents
a. 9 –3/2 = (9 ½ * –3)
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

43. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

44. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

45. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

46. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 =

47. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-2
3

48. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 =
3

49. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 =
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

50. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-3
4
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

51. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-3 = (2)-3
4
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

52. Special Exponents
a. 9 –3/2 = (9 ½ * –3) = (9½)–3 = (9)–3 = 3–3 = 1/27
To calculate a fractional power: extract the root first,
then raise the root to the numerator–power.
Example C. Find the root, then raise the root to the
numerator–power.
By the power–multiply rule, the fractional exponent
A
k
n
±
(A ) k
n ±
1
is
take the nth root of A
then raise the
root to ±k power
c. 16 -3/4 = (161/4)-3 = (16)-3 = (2)-3 = 1/23 = 1/8
4
b. 27 -2/3 = (271/3)-2 = (27)-2 = (3)-2 = 1/32 = 1/9
3

53. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.

54. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8

55. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.

56. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
Example D. Simplify by combining the exponents.

57. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
power–multiply rule
1/3*2 3/2*2
Example D. Simplify by combining the exponents.

58. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
x5/3y3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3

59. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
=
x5/3y3
x5/3 – (–1/2) y3 – 2/3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3
divide–subtract rule

60. a.16–½ =
Fractional Powers
b. 43/2 =
Your turn: calculate the root, then raise the root to the
numerator–power.
Ans: ¼, 8
We use the multiply–add, divide–subtract, and power–
multiply rules to collect fractional exponents.
x*(x1/3y3/2)2
x–1/2y2/3
=
x*x2/3y3
x–1/2y2/3
= x–1/2y2/3
=
x5/3y3
x5/3 – (–1/2) y3 – 2/3
= x13/6 y7/3
Example D. Simplify by combining the exponents.
power–multiply rule
1/3*2 3/2*2
multiply–add rule
1 + 2/3
divide–subtract rule

61. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.

62. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n

63. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 =
b. 9a2 =

64. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 =

65. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2

66. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 =
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

67. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

68. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

69. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
d. Express a2 (a ) as one radical.
3 4
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a

70. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/4
3 4
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.
3 4

71. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/4 = a11/12
3 4
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.
3 4

72. Fractional Powers
Often it’s easier to manipulate radical–expressions
using the fractional exponent notation.
a2 a = a2/3a1/4 = a11/12 = a11
3 4 12
To write a radical in fractional exponent form,
assuming a is defined, we have that:
k
an = ( a )n → a
k k k
n
Example E. Write the following expressions using
fractional exponents then simplify if possible.
c. 9 + a2 = (9 + a2)1/2 ≠ (3 + a ).
a. 53 or (5 )3 = 53/2
b. 9a2 = (9a2)1/2 = 3a
d. Express a2 (a ) as one radical.
3 4

73. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.

74. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 =
b. 16–0.75 =
c. 30.4 =

75. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2
b. 16–0.75 =
c. 30.4 =

76. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3
b. 16–0.75 =
c. 30.4 =

77. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 =
c. 30.4 =

78. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4
c. 30.4 =

79. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3
4
c. 30.4 =

80. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 =

81. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (3)2 ≈ 1.55 (by calculator)
5

82. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (3)2 ≈ 1.55 (by calculator)
5
Working with real numbers and interpreting decimal
exponents as fractions causes problems if the base
is negative.

83. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (3)2 ≈ 1.55 (by calculator)
5
Working with real numbers and interpreting decimal
exponents as fractions causes problems if the base
is negative. For example, (–32)0.2 can be viewed as
(–32)1/5 = –32 = –2, or as (–32)2/10 = (–32)2 which is
not defined.
5 10

84. Decimal Powers
We write decimal–exponents as fractional exponents,
then we extract roots and raise powers as indicated
by the fractional exponents.
Example F. Write the following decimal exponents as
fractional exponents then simplify, if possible.
a. 9–1.5 = 9 –3/2 = (9)–3 = 3–3 = 1/27
b. 16–0.75 = 16 –3/4 = (16)–3 = (2)–3 = 1/8
4
c. 30.4 = 32/5 = (3)2 ≈ 1.55 (by calculator)
5
Working with real numbers and interpreting decimal
exponents as fractions causes problems if the base
is negative. For example, (–32)0.2 can be viewed as
(–32)1/5 = –32 = –2, or as (–32)2/10 = (–32)2 which is
not defined. To avoid this confusion, we assume the
base is positive whenever a decimal exponent is used.
5 10

85. Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.

86. 100 = 1
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with

87. 100 = 1
101 = 10
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with

88. 100 = 1
101 = 10
102 = 100
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with

89. 100 = 1
101 = 10
102 = 100
103 = 1000
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with

90. 100 = 1
101 = 10
102 = 100
103 = 1000
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with
pack 0’s to the right
for positive exponents
so they get larger

91. 100 = 1
101 = 10
102 = 100
103 = 1000
10–1 = 0.1
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with
pack 0’s to the right
for positive exponents
so they get larger

92. 100 = 1
101 = 10
102 = 100
103 = 1000
10–1 = 0.1
10–2 = 0.01
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with
pack 0’s to the right
for positive exponents
so they get larger

93. 100 = 1
101 = 10
102 = 100
103 = 1000
10–1 = 0.1
10–2 = 0.01
10–3 = 0.001
10–4 = 0.0001
Scientific Notation
An important application for exponents is the usage of the
powers of 10 in calculation of very large or very small numbers.
Powers of 10:
starting with
pack 0’s to the right
for positive exponents
so they get larger
pack 0’s to the left for
negative exponents
so they get smaller

97. (Answers to odd problems) Exercise A.
1. 1/2 3. 1/8 5.1/27 7. 1/64 9.3/2
11.1/18 13.1/6
Exercise B.
1. 𝑥8
3. 1/𝑥2
5.𝑥7
/𝑦2
7. 1/𝑥4
9. 𝑥3
11.
1
𝑥7 13.
𝑦8
36𝑥6 15. 2𝑥+3 17. 𝑎2𝑥+3
Exercise C.
1. 8 3. (−8)
2
3 5. 8/27 7. 16 9. 1/8
Exponents

98. Exercise D.
1. 𝑥3 3. 8𝑥4 6
𝑦17 5.
6 𝑦
𝑥3 7. 3𝑎11
2𝑏5
9. 4−5 11.
5
𝑥16 13.
6
(2𝑥 + 1)13 15.
6
sin(𝑥)17
Exercise E.
1.𝑞/𝑝 3. −3 5. 13
7. 2/3 9. 5/6 11. −1/4
Exercise F.
1. 𝑥 = 4, 𝑦 = 2, 𝑧 = 3 3. 𝑥 = 3, 𝑦 = −1, 𝑧 = 6
Exponents