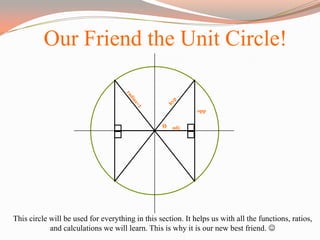
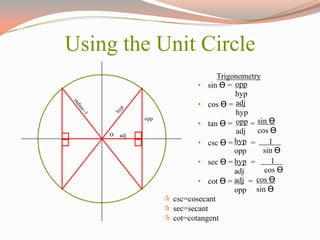
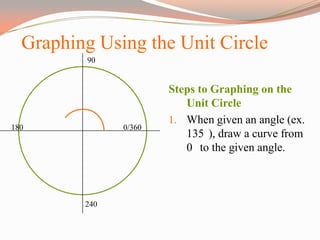
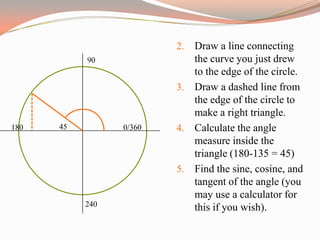
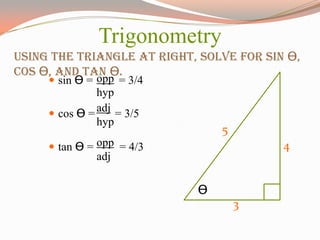
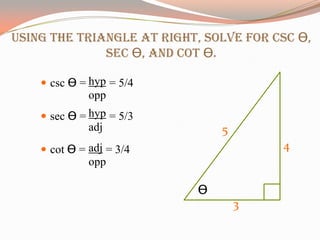
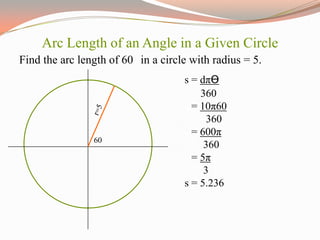
The document provides a comprehensive overview of trigonometric functions, utilizing the unit circle as a foundational tool for understanding sine, cosine, and tangent. It covers graphing angles using the unit circle, converting between radians and degrees, and calculating arc lengths. Additionally, it includes citations for sources and images used in the presentation.

1. Trigonometric FunctionsPre-CalculusAmanda Woodbury

2. Our Friend the Unit Circle!hypradius=1oppƟadjThis circle will be used for everything in this section. It helps us with all the functions, ratios, and calculations we will learn. This is why it is our new best friend. 

3. Using the Unit CircleTrigonometrysin Ɵ =

4. cos Ɵ =

5. tan Ɵ = =

6. csc Ɵ = =

7. sec Ɵ = =

8. cot Ɵ = = opphypadjhypsin Ɵcos Ɵoppadjhypopp 1 1sin Ɵ 1 1cos Ɵhypadjcos Ɵsin Ɵadjoppcsc=cosecant

9. sec=secant

10. cot=cotangentGraphing Using the Unit Circle 90°180° 0/360° 240°Steps to Graphing on the Unit CircleWhen given an angle (ex. 135°), draw a curve from 0° to the given angle.

11. Draw a line connecting the curve you just drew to the edge of the circle.Draw a dashed line from the edge of the circle to make a right triangle.Calculate the angle measure inside the triangle (180-135 = 45)Find the sine, cosine, and tangent of the angle (you may use a calculator for this if you wish). 90°180° 0/360° 240°45°

12. TrigonometryUsing the triangle at right, solve for sin Ɵ, cosƟ, and tanƟ.opphypsin Ɵ = = 3/4cosƟ = = 3/5 tan Ɵ = = 4/3adjhyp5oppadj4Ɵ3

13. Using the triangle at right, solve for cscƟ, sec Ɵ, and cot Ɵ.hypoppcscƟ = = 5/4secƟ = = 5/3cotƟ = = 3/4hypadj54adjoppƟ3

14. Radian MeasureRadians use π ratios instead of degrees and are fractions, not whole numbers , π,2π,etc…π , π , π ,π, 3π, 5π6 4 3 2 4 6

15. Degree MeasureDegrees do not use π ratios and are whole numbers instead of fractions15°, 30°, 45°, 60°, 90°, 120°, 180°, 360°, etc… 90°180° 0/360° 240°

16. Converting between Radians and DegreesWhen converting from Radians to Degrees:Multiply the radian ratio by 180Divide the radian ratio by πThe two π symbols will cancel each other out and all that will be left is a simple mathematical equationExample: = = 150°5π6180π5(180) 6