The document discusses using sign charts to solve polynomial and rational inequalities. It provides examples of solving inequalities by setting one side equal to zero, factoring the expression, drawing the sign chart, and determining the solutions from the regions with the appropriate signs. Specifically, it works through examples of solving x^2 - 3x > 4, 2x^2 - x^3/(x^2 - 2x + 1) < 0, and (x - 2)/(2/(x - 1)) < 3.

1. Inequalities and Sign Charts
Math 260
Dr. Frank Ma
LA Harbor College

2. The easiest way to solve a polynomial or rational
inequality is to use the sign–chart.
Inequalities and Sign Charts

3. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart.
Inequalities and Sign Charts

4. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
Inequalities and Sign Charts

5. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
Setting one side to 0, we have x2 – 3x – 4 > 0
Inequalities and Sign Charts

6. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression
Setting one side to 0, we have x2 – 3x – 4 > 0
Inequalities and Sign Charts

7. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0.
Inequalities and Sign Charts

8. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression and draw the sign–chart,
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0.
Inequalities and Sign Charts

9. Example A. Solve x2 – 3x > 4
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression and draw the sign–chart,
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0. The roots are x = –1, 4 both are
odd power roots.
Inequalities and Sign Charts

10. Example A. Solve x2 – 3x > 4
4 (odd power)
–1 (odd power) 5
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression and draw the sign–chart,
(x – 4)(x + 1)
+ + + – – – – – – + + + +
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0. The roots are x = –1, 4 both are
odd power roots. Sample x = 5, we get +,
completing the signs:
Inequalities and Sign Charts

11. Example A. Solve x2 – 3x > 4
4 (odd power)
–1 (odd power) 5
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression and draw the sign–chart,
(x – 4)(x + 1)
+ + + – – – – – – + + + +
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0. The roots are x = –1, 4 both are
odd power roots. Sample x = 5, we get +,
completing the signs:
Inequalities and Sign Charts

12. Example A. Solve x2 – 3x > 4
4 (odd power)
–1 (odd power)
The solutions are the + regions: (–∞, –1) U (4, ∞)
5
4
–1
The easiest way to solve a polynomial or rational
inequality is to use the sign–chart. To do this,
I. set one side of the inequality to 0,
II. factor the expression and draw the sign–chart,
III. read off the answer from the sign chart.
(x – 4)(x + 1)
+ + + – – – – – – + + + +
Setting one side to 0, we have x2 – 3x – 4 > 0 or
(x – 4)(x + 1) > 0. The roots are x = –1, 4 both are
odd power roots. Sample x = 5, we get +,
completing the signs:
Inequalities and Sign Charts

13. The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Inequalities and Sign Charts

14. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0

15. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression:

16. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2

17. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)

18. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered).

19. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered).

20. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ".
x=0 (even) x=2 (odd)
x= 1 (even) x=3

21. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ". Complete the sign-chart.
x=0 (even) x=2 (odd)
x= 1 (even) x=3

22. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ". Complete the sign-chart.
x=0 (even) x=2 (odd)
x= 1 (even)
+ change
x=3

23. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ". Complete the sign-chart.
x=0 (even) x=2 (odd)
x= 1 (even)
+ change
unchanged
+
x=3

24. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ". Complete the sign-chart.
x=0 (even) x=2 (odd)
x= 1 (even)
+ change
unchanged
unchanged
+
+
x=3

25. Inequalities and Sign Charts
The theorem may be generalized to rational formulas
that are factorable, that is, both the numerator and
the denominator are factorable.
Example B. Solve the inequality 2x2 – x3
x2 – 2x + 1
< 0
Factor the expression: 2x2 – x3
x2 – 2x + 1
= x2(2 – x)
(x – 1)2
Roots of the numerator are x = 0 (even-ordered)
and x = 2 (odd-ordered). The root of the
denominator is x = 1 (even-ordered). Draw and
test x = 3, we get " – ". Complete the sign-chart.
x=0 (even) x=2 (odd)
x= 1 (even)
+ change
unchanged
unchanged
+
+
Hence the solution is 2 < x.
x=3

26. Example C. Solve x – 2
2 <
x – 1
3
Inequalities and Sign Charts

27. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Inequalities and Sign Charts

28. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
Inequalities and Sign Charts

29. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
Inequalities and Sign Charts

30. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
=
(x – 2)(x – 1)
– x + 4
Inequalities and Sign Charts

31. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
=
(x – 2)(x – 1)
– x + 4
Hence the inequality is (x – 2)(x – 1)
– x + 4 < 0
Inequalities and Sign Charts

32. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
=
(x – 2)(x – 1)
– x + 4
Hence the inequality is (x – 2)(x – 1)
– x + 4 < 0
It has a root at x = 4, it's undefined at x = 1, 2
and all of them are of odd–power.
4
1 2
UDF UDF
(x – 2)(x – 1)
– x + 4
Inequalities and Sign Charts

33. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
=
(x – 2)(x – 1)
– x + 4
Hence the inequality is (x – 2)(x – 1)
– x + 4 < 0
It has a root at x = 4, it's undefined at x = 1, 2
and all of them are of odd–power.
Testing x = 5, we get –, so the sign–chart is:
4
1
0 5
+ + + – – + + + + – – – –
2
UDF UDF
(x – 2)(x – 1)
– x + 4
Inequalities and Sign Charts

34. Example C. Solve x – 2
2 <
x – 1
3
Set the inequality to 0, x – 2
2
x – 1
3
< 0
Put the expression into factored form,
x – 2
2
x – 1
3
=
(x – 2)(x – 1)
2(x – 1) – 3(x – 2)
=
(x – 2)(x – 1)
– x + 4
Hence the inequality is (x – 2)(x – 1)
– x + 4 < 0
It has a root at x = 4, it's undefined at x = 1, 2
and all of them are of odd–power.
Testing x = 5, we get –, so the sign–chart is:
4
1
0 5
+ + + – – + + + + – – – –
2
UDF UDF
(x – 2)(x – 1)
– x + 4
The answer are the shaded intervals or (1, 2) U [4 ∞).
Inequalities and Sign Charts

35. Exercise A. Use the sign–charts method to solve the
following inequalities.
1. (x – 2)(x + 3) > 0
3. (2 – x)(x + 3) ≥ 0
8. x2(2x – 1)2(3 – x) ≤ 0
9. x2 – 2x < 3
14. 1 <
13. x4 > 4x2
(2 – x)
(x + 3)
2.
–x
(x + 3)
4.
7. x2(2x – 1)(3 – x) ≥ 0
1
x 15. 2 2
x – 2
16. 1
x + 3
2
x – 2
17. >
2
x – 4
1
x + 2
5. x(x – 2)(x + 3)
x
(x – 2)(x + 3)
6. ≥ 0
10. x2 + 2x > 8
11. x3 – 2x2 < 3x 12. 2x3 < x2 + 6x
≥
≥ 0
≤ 0
≤ 0
≤ 18. 1 < 1
x2
Inequalities and Sign Charts

36. B. Solve the inequalities, use the answers from Ex.1.3.
Inequalities and Sign Charts

37. 5. 6. (x – 2)2
x2(x – 6)
x + 6
x(x + 5)2
7.
(1 – x2)3
x2
C. Solve the following inequalities using sign–charts.
1. x2(x + 2) > 0 2. 0 > (x + 2)2(x – 5)3
4. 0 ≤ 2x4 – 8x2
3. x2(x – 4)3 ≤ 0
> 0
≥ 0
≤ 0
8.
x4 – x2
(x + 3)2(6 – x)
≤ 0
D. In order for the formula √R to be defined, the radicand R
must be ≥ 0. Draw the domain of the following formulas.
5. 6.
(x – 2)2
x2(x – 6)
x + 6
x(x + 5)2
7. x2
1. √x2(x + 2) 2. √(x + 2)2(x – 5)3
4. √2x4 – 8x2
3. √ x2(x – 4)3
8. (x + 3)2(6 – x)
x4 – x2
(1 – x2)3
√ √
√ √
Inequalities and Sign Charts

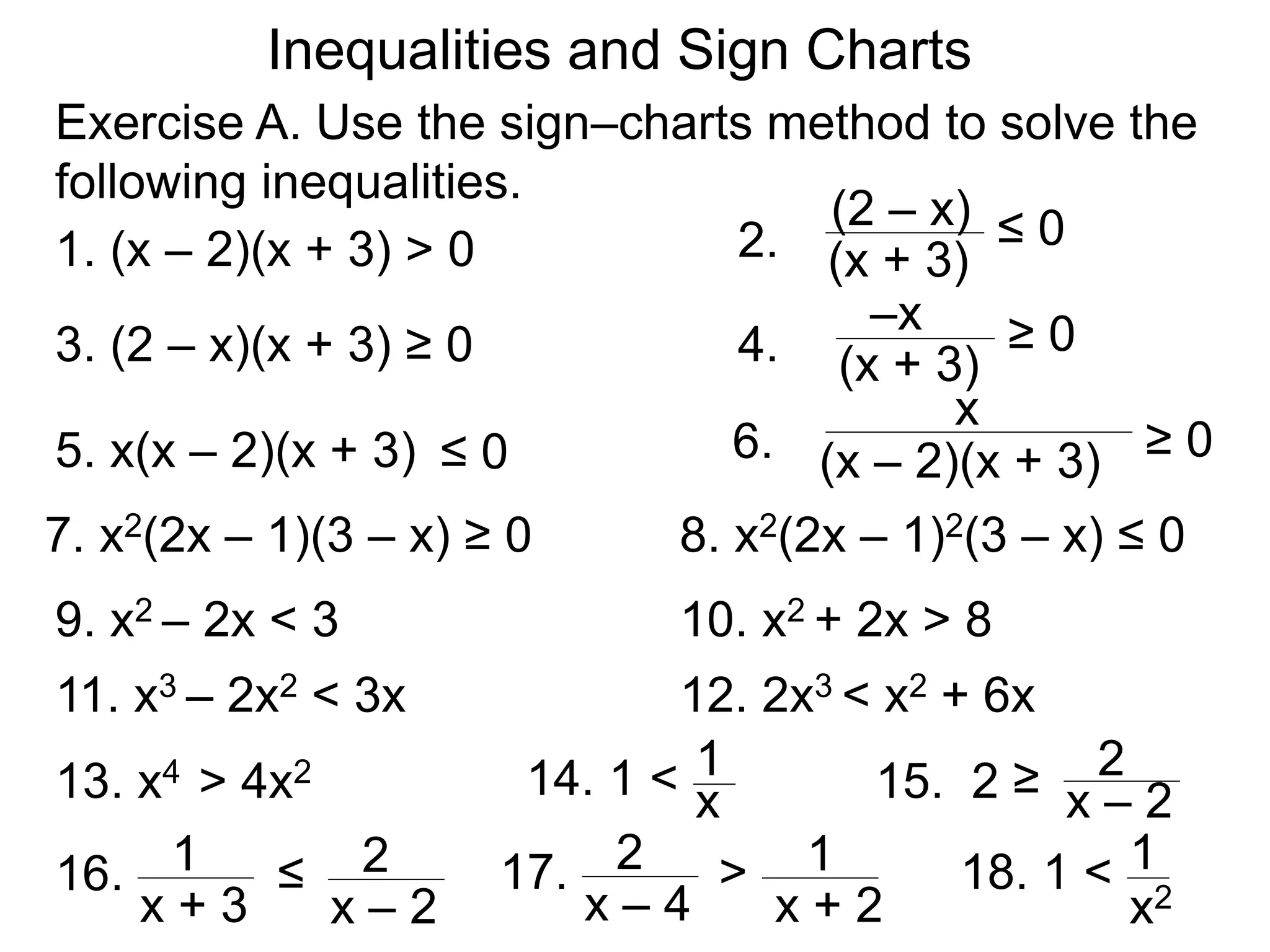
38. Answers: Exercise A.
1. (–∞, –3) ∪ (2, ∞) 3. [–3, 2] 5. (–∞, –3] ∪ [0, 2]
9. (–1, 3)
7. {0} ∪ [1/2, 3] 11. (–∞, –1) ∪ (0, 3)
13. (–∞, –2) ∪ (2, ∞) 15. (–∞, 2) ∪ [3, ∞)
17. (–8, –2) ∪ (4, ∞)
Exercise B.
1. The statement is not true. No such x exists.
3. (–∞, – 12/5) ∪ (2, ∞)
5. (2, 13/3]
Inequalities and Sign Charts

39. Exercise C.
3. 𝑥2(𝑥 − 4)3 ≤ 0
1. 𝑥2 𝑥 – 2 > 0
x=0 x=2
+
The solution is (2, ∞)
x=0 x=4
+
The solution is −∞, 4
Inequalities and Sign Charts

40. 5.
𝑥2(𝑥−6)
𝑥+6
> 0
The solution is (−∞, −6) ∪ (6, ∞)
x= – 6 x=6
x= 0
+
+ UDF f=0 f=0
7.
𝑥2
(1−𝑥2)3 ≥ 0
x= – 1 x=1
x= 0
+
UDF f=0 UDF
+
The solution is (−1, 1)
Inequalities and Sign Charts

41. Exercise D.
1. 𝑥2(𝑥 + 2)
3. 𝑥2(𝑥 − 4)3
x= –2
x=4
x=-6 x=6
x=-1 x=1
5.
𝑥2(𝑥−6)
𝑥+6
7.
𝑥2
(1−𝑥2)3
Inequalities and Sign Charts
x=0
x=0