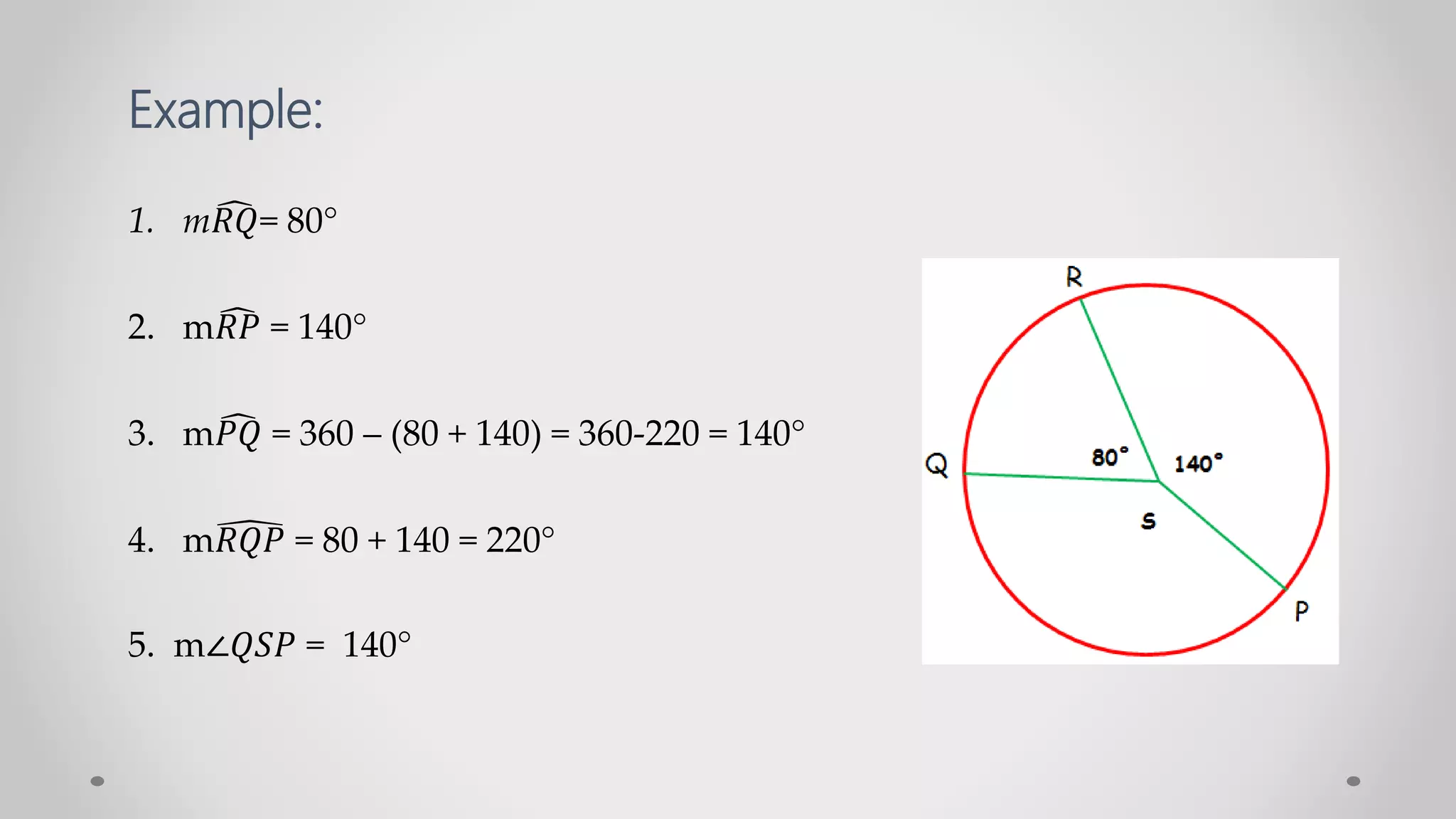
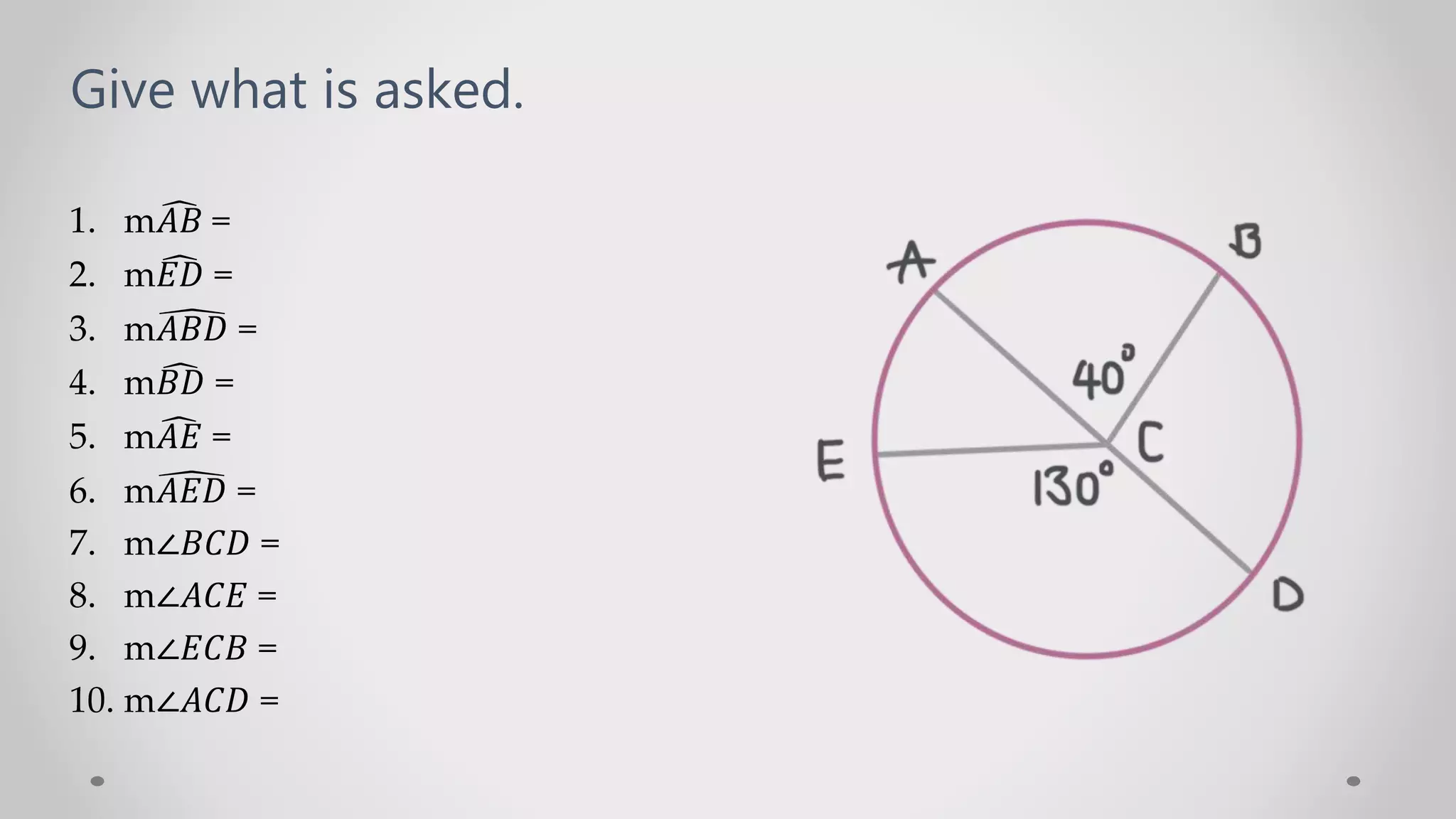
The document discusses circles and arcs. It defines a central angle as an angle whose vertex is the center of a circle. A minor arc is the portion of a circle between two points that is interior to the central angle, while a major arc is exterior to the central angle. The measure of an arc, in degrees, is equal to the measure of its central angle. A semicircle has a measure of 180 degrees. Two arcs are congruent if they have the same degree measure.

2. Let’s Learn
Given a circle with center P. Let us
consider ∠𝐴𝑃𝐵. It is called a central angle of the
circle. The vertex of the angle is point P.
Let us considered points A, B and C on the
circle. The union of points A, B and all points of the
circle in the interior of ∠𝐴𝑃𝐵 is called minor arc. To
denote minor arc we write 𝑨𝑩.
The major arc is the union of points A, B
and all the points on the circle in the exterior of
∠𝐴𝑃𝐵. To denote major arc, we write 𝐴𝐶𝐵.

3. In each case both, A and C are the end
points of both minor and major arcs.
Arcs of a circle and the central angle that
intercept them are related in special way.
The measure of an arc, in degrees, is
numerically equal to the measure of the
corresponding central arc.
So, if m∠𝐴𝑃𝐵 = 60°, the measure of the
corresponding minor arc 𝐴𝐵 is also 60°.
The degree measure of a major arc is
equal to 360° minus the measure of the
corresponding minor arc.

4. If A and B are the endpoints of a diameter,
then we have two arcs each of which is called
semicircle or half circle.
The degree measure of a semicircle is 180°.
The entire circle has an arc measure of 360°.
The degree measure of a major arc is equal to 360°
minus the measure of the corresponding minor arc.
In the same or congruent circles, two arcs
are congruent if they have the same measure.
Thus, if m𝐶𝐵 ≅ m𝐷𝐸, then 𝐶𝐵 ≅ 𝐷𝐸.
Also, ∠𝐶𝐴𝐵 ≅ ∠𝐷𝐴𝐸.

5. Example:
1. m𝑅𝑄= 80°
2. m𝑅𝑃 = 140°
3. m𝑃𝑄 = 360 – (80 + 140) = 360-220 = 140°
4. m𝑅𝑄𝑃 = 80 + 140 = 220°
5. m∠𝑄𝑆𝑃 = 140°

6. Give what is asked.
1. m𝐴𝐵 =
2. m𝐸𝐷 =
3. m𝐴𝐵𝐷 =
4. m𝐵𝐷 =
5. m𝐴𝐸 =
6. m𝐴𝐸𝐷 =
7. m∠𝐵𝐶𝐷 =
8. m∠𝐴𝐶𝐸 =
9. m∠𝐸𝐶𝐵 =
10. m∠𝐴𝐶𝐷 =