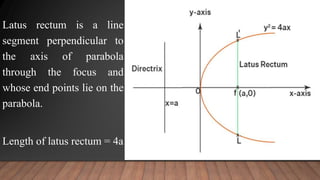
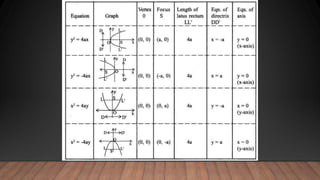
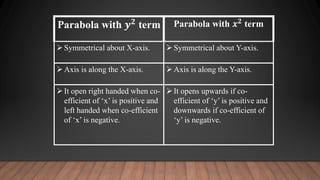
A parabola is a set of points equidistant from a fixed line (the directrix) and a fixed point (the focus) not on the line. The key properties of a parabola include its focus, directrix, vertex, axis, and latus rectum. There are four types of parabolas defined by the position of the vertex and axis. Parabolas have many applications in fields like antennas, microphones, vehicle headlights, and ballistics due to their shape.

2. Topic : Parabola

3.  Definition: A parabola is a set of all points in a plane
that are equidistant from a fixed line and a
fixed point (not on the line) in the plane.
'Para' means 'for'
'Bola' means 'throwing'
Parabola means shape describe
when we throw a ball in the air.

4.  The fixed line is called directrix of the parabola and fixed point f is called
focus.
 Latus rectum is a line segment perpendicular to the axis of parabola
through the focus and whose end points lie on the parabola.
Key Terms
 A point of intersection of a conic with its axis is
called vertex.
 The line passing through the focus and
perpendicular to the directrix is called axis.
 The constant ratio is called eccentricity denoted
with the letter e.

5. Deriving standard equation of a parabola

6. Latus rectum is a line
segment perpendicular to
the axis of parabola
through the focus and
whose end points lie on the
parabola.
Length of latus rectum = 4a

8. Types of parabola : 1) Right-open parabola
Vertex: (0,0)
Focus: (a,0)
Axis: Y=0
Equation of directrix: x = -a
Length of latus rectum = 4a
𝒚𝟐 = 𝟒𝒂𝒙

9. y
2) Find the equation of the parabola
with focus (2,0), directrix x=-2.
𝑦2
= 12𝑥
1)

10. 2) Left-open parabola
Vertex: (0,0)
Focus: (-a,0)
Axis: Y=0
Equation of directrix: x = a
Length of latus rectum = 4a
𝒚𝟐 = −𝟒𝒂𝒙

11. 2) Find the equation of the parabola
with vertex (0,0) and directrix x=8.
1) 𝑦2
= 15𝑥

12. 3) Open-upwards parabola
Vertex: (0,0)
Focus: (0,a)
Axis: X=0
Equation of directrix: y = -a
Length of latus rectum = 4a
𝒙𝟐 = 𝟒𝒂𝒚

13. 2) Find the equation of the parabola
with vertex (0,0) and directrix y=-9.
1) 𝑥2
= 5𝑦

14. 4) Open-downward parabola
Vertex: (0,0)
Focus: (0,-a)
Axis: X=0
Equation of directrix: y = a
Length of latus rectum = 4a
𝒙𝟐
= −𝟒𝒂𝒚

16. Applications
 The parabola has many important applications, from a
parabolic antenna or parabolic microphone to
automobile headlight reflectors and the design of
ballistic missiles.
 It is frequently used in physics, engineering, and many
other areas.

17. Parabola with 𝒚𝟐
term Parabola with 𝒙𝟐 term
Symmetrical about X-axis. Symmetrical about Y-axis.
Axis is along the X-axis. Axis is along the Y-axis.
It open right handed when co-
efficient of ‘x’ is positive and
left handed when co-efficient
of ‘x’ is negative.
It opens upwards if co-
efficient of ‘y’ is positive and
downwards if co-efficient of
‘y’ is negative.

18.  Indian track and field athlete Neeraj Chopra, who
competes in the javelin throw, won a gold medal
at Tokyo Olympics. He is the first track and field
athlete to win a gold medal for India at the
Olympics.
 Based on above information, answer the following
1. Name the shape of paths followed by javelin.
2. If the equation of such a curve is given by 𝑥2
= −16𝑦, then
write the coordinate of foci.
3. Write the equation of directrix and length of semi-latus rectum.
Case Study