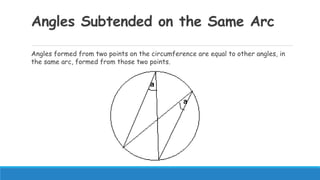
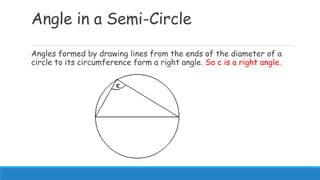
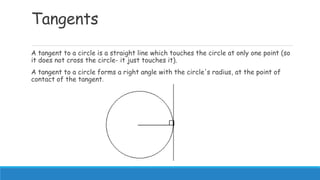
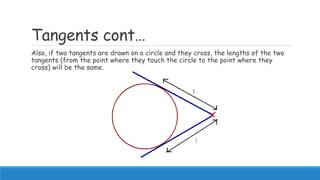
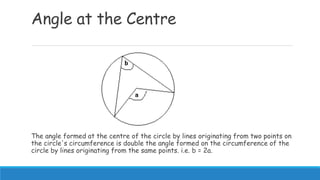
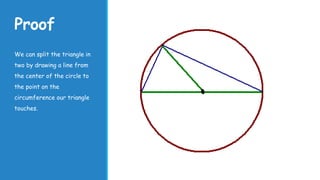
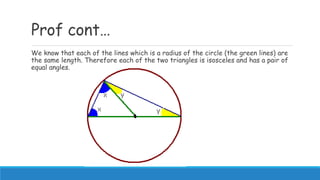
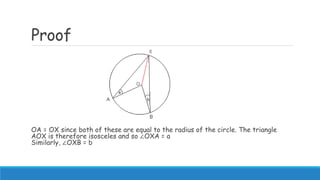
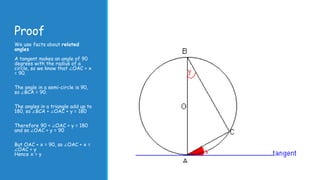
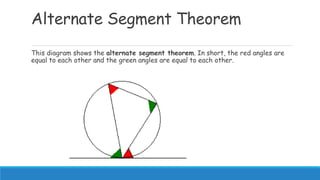
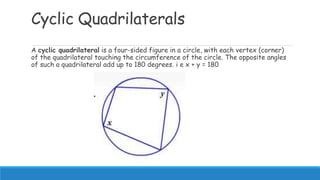
1) Laws of circle geometry include angles subtended on the same arc being equal, angles formed by a diameter and circumference forming a right angle, and tangents forming right angles with radii. 2) Proofs for these laws involve splitting triangles formed using radii and points on the circumference into isosceles triangles, and using properties of angles in triangles and circles. 3) Additional circle geometry concepts covered are tangents only touching circles at one point, alternate segment theorem stating corresponding angles are equal, and cyclic quadrilaterals having opposite angles summing to 180 degrees.

1. Circle Geometry
LAWS OF CIRCLE GEOMETRY

2. Angles Subtended on the Same Arc
Angles formed from two points on the circumference are equal to other angles, in
the same arc, formed from those two points.

3. Angle in a Semi-Circle
Angles formed by drawing lines from the ends of the diameter of a
circle to its circumference form a right angle. So c is a right angle.

4. Proof
We can split the triangle in
two by drawing a line from
the center of the circle to
the point on the
circumference our triangle
touches.

5. Prof cont…
We know that each of the lines which is a radius of the circle (the green lines) are
the same length. Therefore each of the two triangles is isosceles and has a pair of
equal angles.

6. * Note…
But all of these angles together must add up to 180°, since they are
the angles of the original big triangle.
Therefore x + y + x + y = 180, in other words 2(x + y) = 180.
and so x + y = 90. But x + y is the size of the angle we wanted to find.

7. Tangents
A tangent to a circle is a straight line which touches the circle at only one point (so
it does not cross the circle- it just touches it).
A tangent to a circle forms a right angle with the circle's radius, at the point of
contact of the tangent.

8. Tangents cont…
Also, if two tangents are drawn on a circle and they cross, the lengths of the two
tangents (from the point where they touch the circle to the point where they
cross) will be the same.

9. Angle at the Centre
The angle formed at the centre of the circle by lines originating from two points on
the circle's circumference is double the angle formed on the circumference of the
circle by lines originating from the same points. i.e. b = 2a.

10. Proof
OA = OX since both of these are equal to the radius of the circle. The triangle
AOX is therefore isosceles and so ∠OXA = a
Similarly, ∠OXB = b

11. Prof cont…
Since the angles in a triangle add up to 180, we know that ∠XOA = 180 - 2a
Similarly, ∠BOX = 180 - 2b
Since the angles around a point add up to 360, we have that ∠AOB = 360 - ∠XOA -
∠BOX
= 360 - (180 - 2a) - (180 - 2b)
= 2a + 2b = 2(a + b) = 2 ∠AXB

12. Alternate Segment Theorem
This diagram shows the alternate segment theorem. In short, the red angles are
equal to each other and the green angles are equal to each other.

13. Proof
We use facts about related
angles
A tangent makes an angle of 90
degrees with the radius of a
circle, so we know that ∠OAC + x
= 90.
The angle in a semi-circle is 90,
so ∠BCA = 90.
The angles in a triangle add up to
180, so ∠BCA + ∠OAC + y = 180
Therefore 90 + ∠OAC + y = 180
and so ∠OAC + y = 90
But OAC + x = 90, so ∠OAC + x =
∠OAC + y
Hence x = y

14. Cyclic Quadrilaterals
A cyclic quadrilateral is a four-sided figure in a circle, with each vertex (corner)
of the quadrilateral touching the circumference of the circle. The opposite angles
of such a quadrilateral add up to 180 degrees. i e x + y = 180

15. Area of Sector and Arc Length
if the radius of the circle is r,
Area of sector = πr2 × A/360
Arc length = 2πr × A/360
In other words, area of sector = area of circle × A/360
arc length = circumference of circle × A/360

16. The end