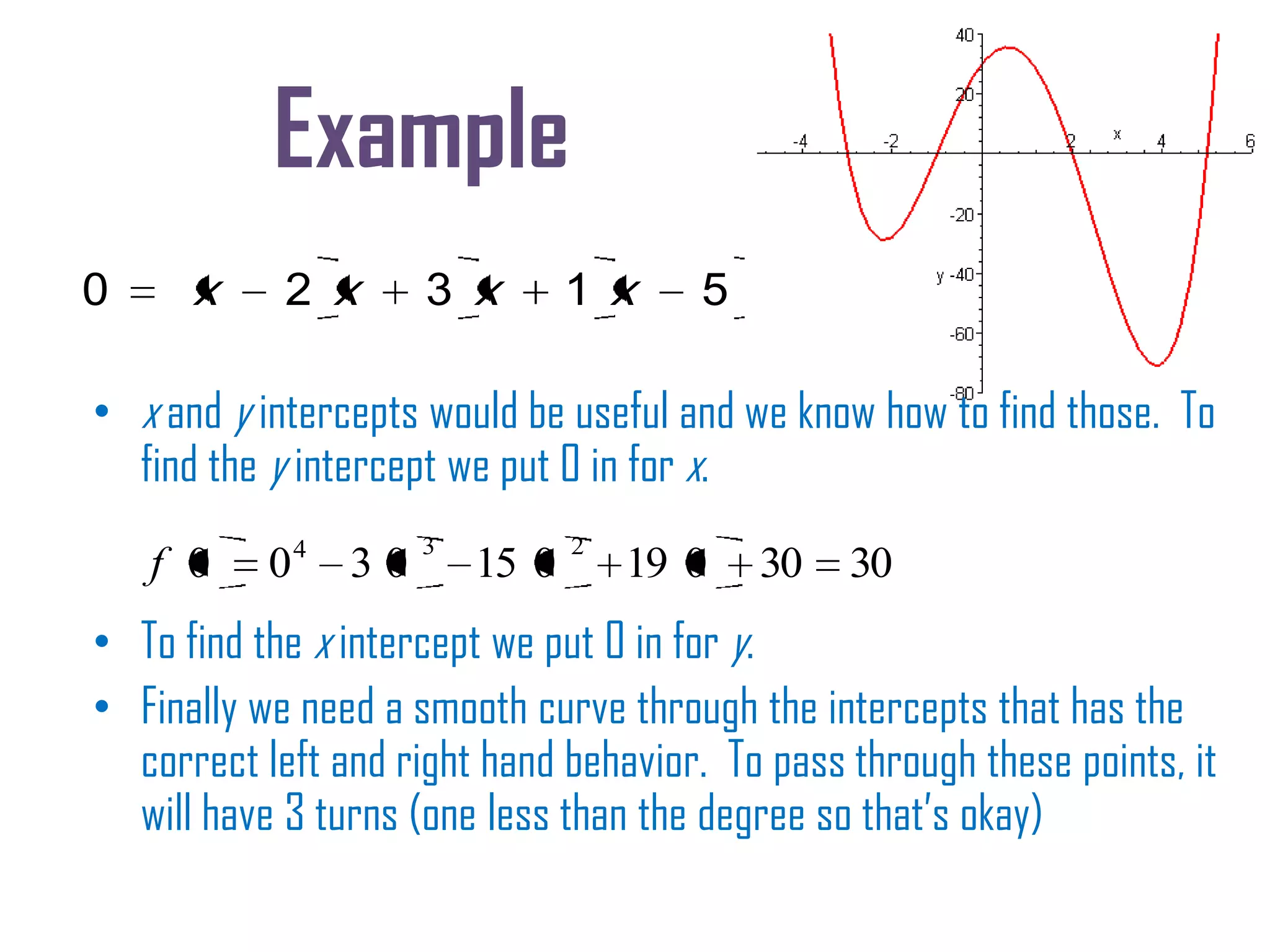
This document provides an overview of key concepts related to graphing polynomials, including: 1. Definitions of terms like intervals of increase/decrease, odd/even functions, zeros, and multiplicities. 2. Steps for graphing polynomials which include determining behavior, finding intercepts and zeros, and joining points based on multiplicities. 3. Examples are provided to demonstrate finding zeros and their multiplicities, and graphing a polynomial based on the identified features. 4. Information that can be determined from a polynomial graph, such as degree, leading coefficient, end behavior, intercepts, and intervals of increase/decrease.

1. Advanced FunctionsE-PresentationPrepared by: Part IITan Yu HangTai Tzu YingWendy Victoria VazTan Hong YeeVoonKhai SamWei Xin

2. 1.3Equations and Graphs of Polynomials

3. Definitionsinterval of increase: an interval over the domain of a function where the value of the function is strictly increasing (going from left to right).interval of decrease: an interval over the domain of a function where the value of the function is strictly decreasing (going from left to right). odd function: all odd functions have rotational symmetry about the origin and satisfy the equation f (−x) = − f (x) .even function: all even functions have symmetry about the y-axis and satisfy the equation f (−x) = f (x) .

4. Examplex and y intercepts would be useful and we know how to find those. To find the y intercept we put 0 in for x.To find the x intercept we put 0 in for y. Finally we need a smooth curve through the intercepts that has the correct left and right hand behavior. To pass through these points, it will have 3 turns (one less than the degree so that’s okay)

5. ExampleWe found the x intercept by putting 0 in for f(x) or y (they are the same thing remember). So we call the x intercepts the zerosof the polynomial since it is where it = 0. These are also called the rootsof the polynomial.Can you find the zeros of the polynomial?There are repeated factors. (x-1) is to the 3rd power so it is repeated 3 times. If we set this equal to zero and solve we get 1. We then say that 1 is a zero of multiplicity 3 (since it showed up as a factor 3 times).What are the other zeros and their multiplicities?-2 is a zero of multiplicity 2 3 is a zero of multiplicity 1

6. So knowing the zeros of a polynomial we can plot them on the graph. If we know the multiplicity of the zero, it tells us whether the graph crossesthe x axis at this point (odd multiplicities CROSS) or whether it just touchesthe axis and turns and heads back the other way (even multiplicities TOUCH). Let’s try to graph:What would the left and right hand behavior be?You don’t need to multiply this out but figure out what the highest power on an x would be if multiplied out. In this case it would be an x3. Notice the negative out in front.

7. Steps for Graphing a PolynomialDetermine left and right hand behavior by looking at the highest power on x and the sign of that term.

8. Determine maximum number of turning points in graph by subtracting 1 from the degree.

9. Find and plot y intercept by putting 0 in for x

10. Find the zeros (x intercepts) by setting polynomial = 0 and solving.

11. Determine multiplicity of zeros

12. Join the points together in a smooth curve touching or crossing zeros depending on multiplicity and using left and right hand behavior as a guide.Let’s graphJoin the points together in a smooth curve touching or crossing zeros depending on multiplicity and using left and right hand behavior as a guide.Here is the actual graph. We did pretty good. If we’d wanted to be more accurate on how low to go before turning we could have plugged in an x value somewhere between the zeros and found the y value. We are not going to be picky about this though since there is a great method in calculus for finding these maximum and minimum.

13. What can we get from the graph ?Degree of the polynomial functionSign of leading coefficientEnd BehaviorX and Y interceptsIntervals

14. 1.Degree of the polynomial function EVEN-DEGREEThis is a EVEN root polynomial function.

15. Even-degree polynomials are either facing up or down on both ends.ODD-DEGREEOdd-Degree polynomial have a type of graph by which both the end is at the opposite side.2.Sign of leading coefficientPOSITIVE COEFFICIENTNEGATIVE COEFFICIENT

16. 3.End BehaviorCan be determined through the end of the by which it extended from quadrant _ to quadrant _Quadrant 1 Quadrant 2 Quadrant 4 Quadrant 3

17. 4. X and Y interceptsIf a polynomial function has a factor (x-a) that is repeated n times, then x=a is a zero of order. Example:(x-2)2=0 has a zero of order 2 at x=2.

18. 5.Intervals For Example: Y=(X+1)1(X-1)intervalX<1-1<X<1X>1Choose a number which is smaller/lesser than -1 and sub into the equation. Then determine whether it is +/-Choose a number between -1 and +1. then do the same thing again as you did it one the previous column.Sign of leading coefficientChoose a number which is bigger/more than 1 and substitute it into the polynomial equation.

19. The End. Hope you enjoyed our Advanced Functions E-Presentation and learnt something!