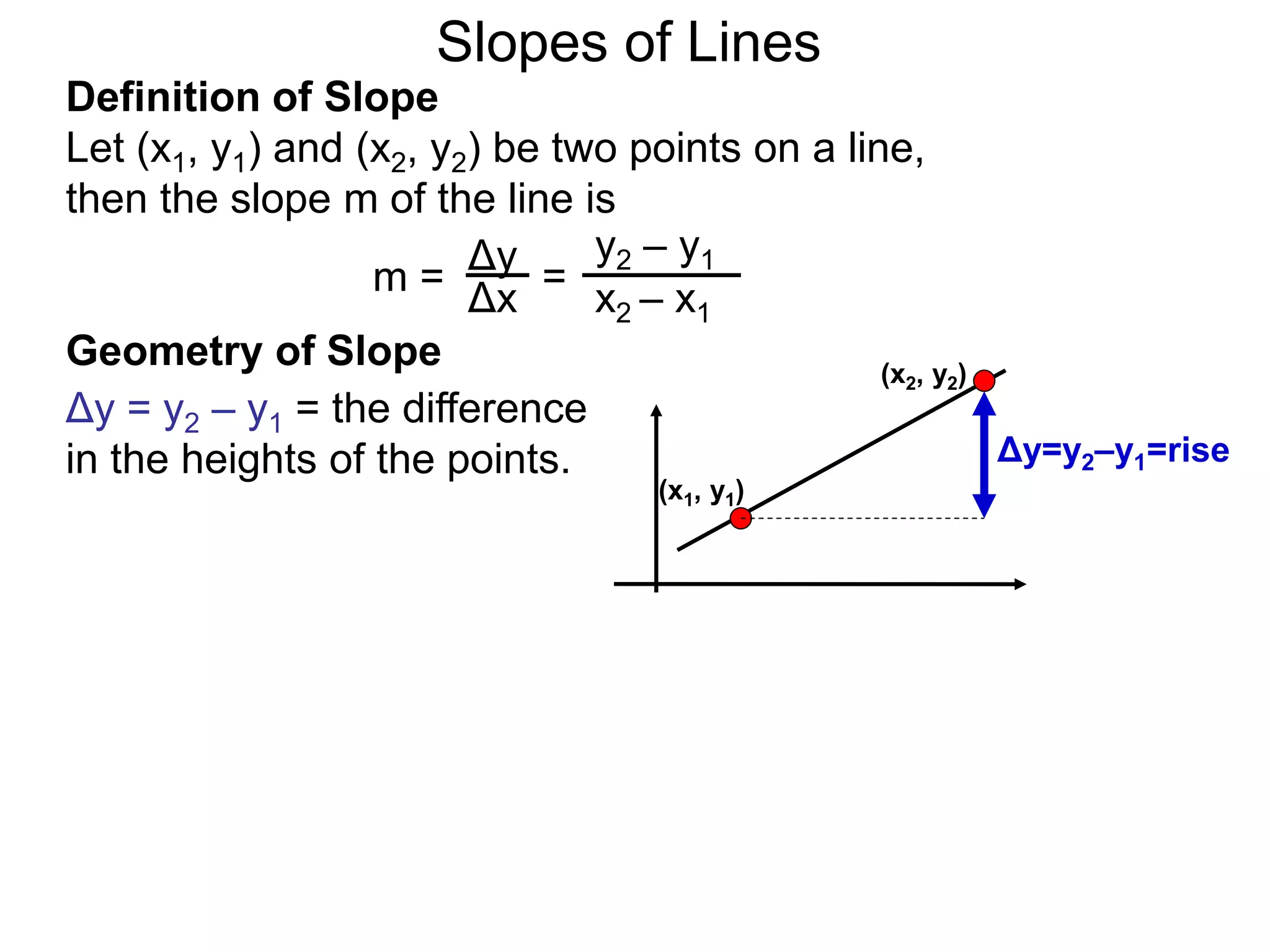
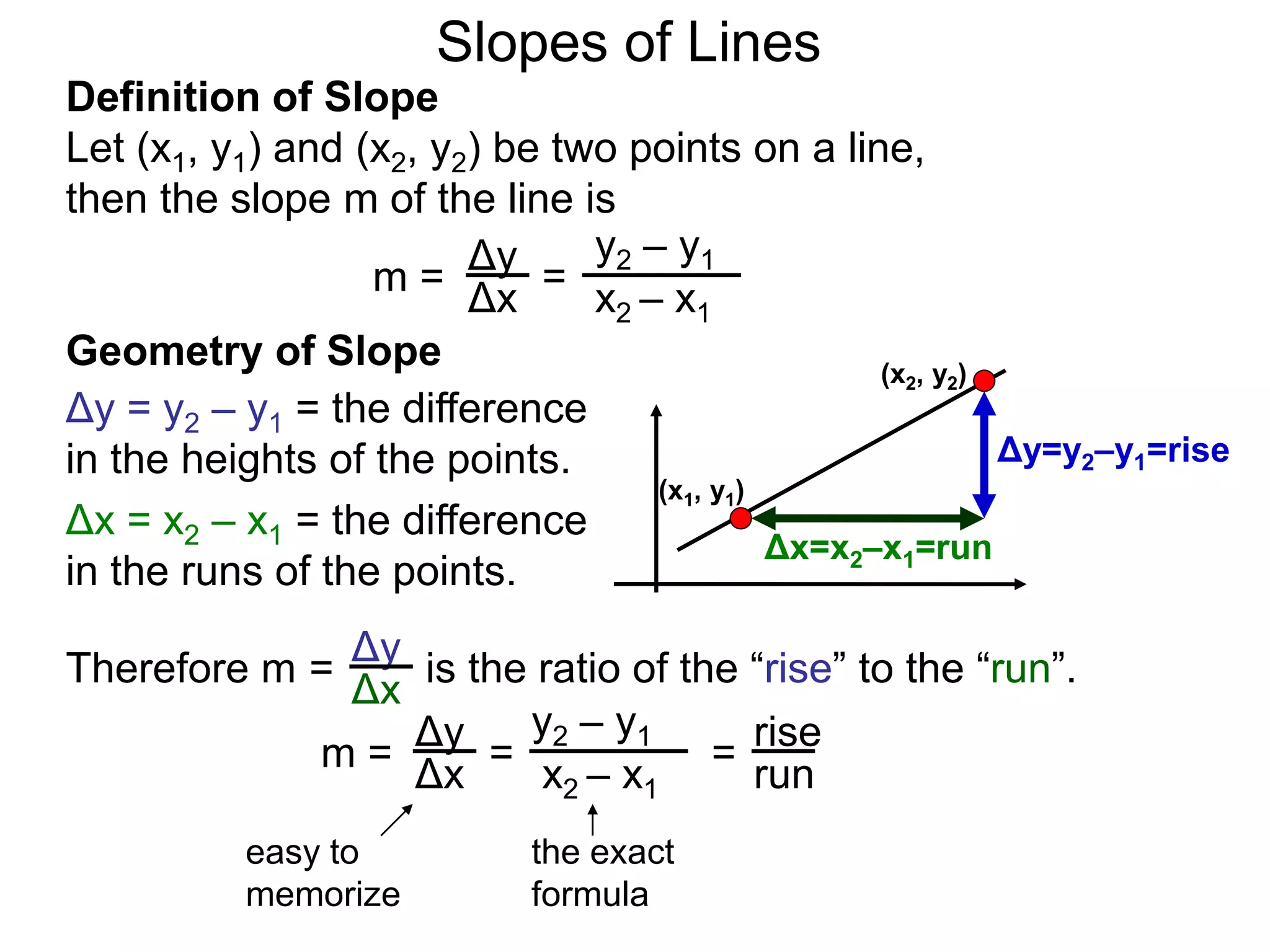
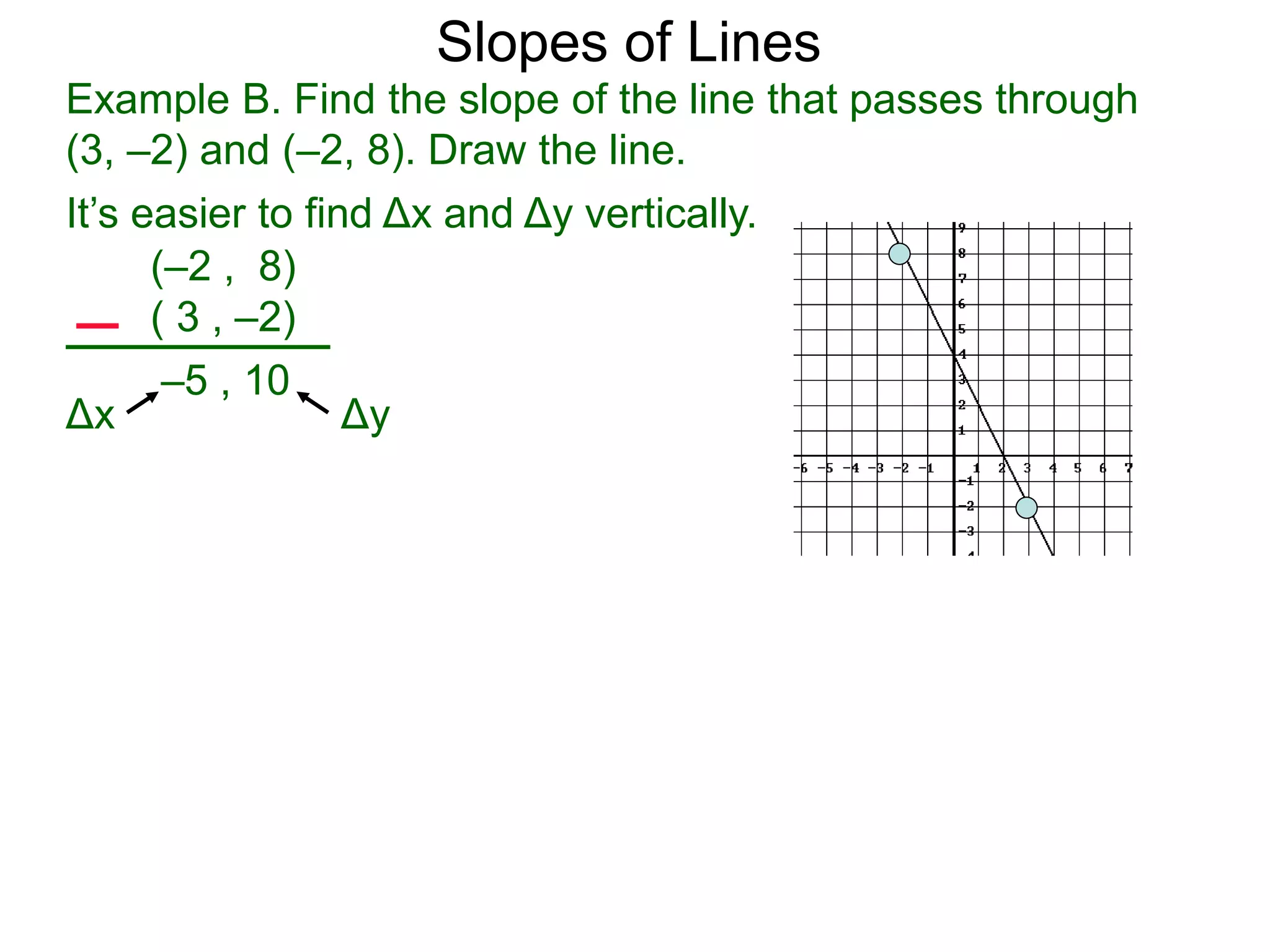
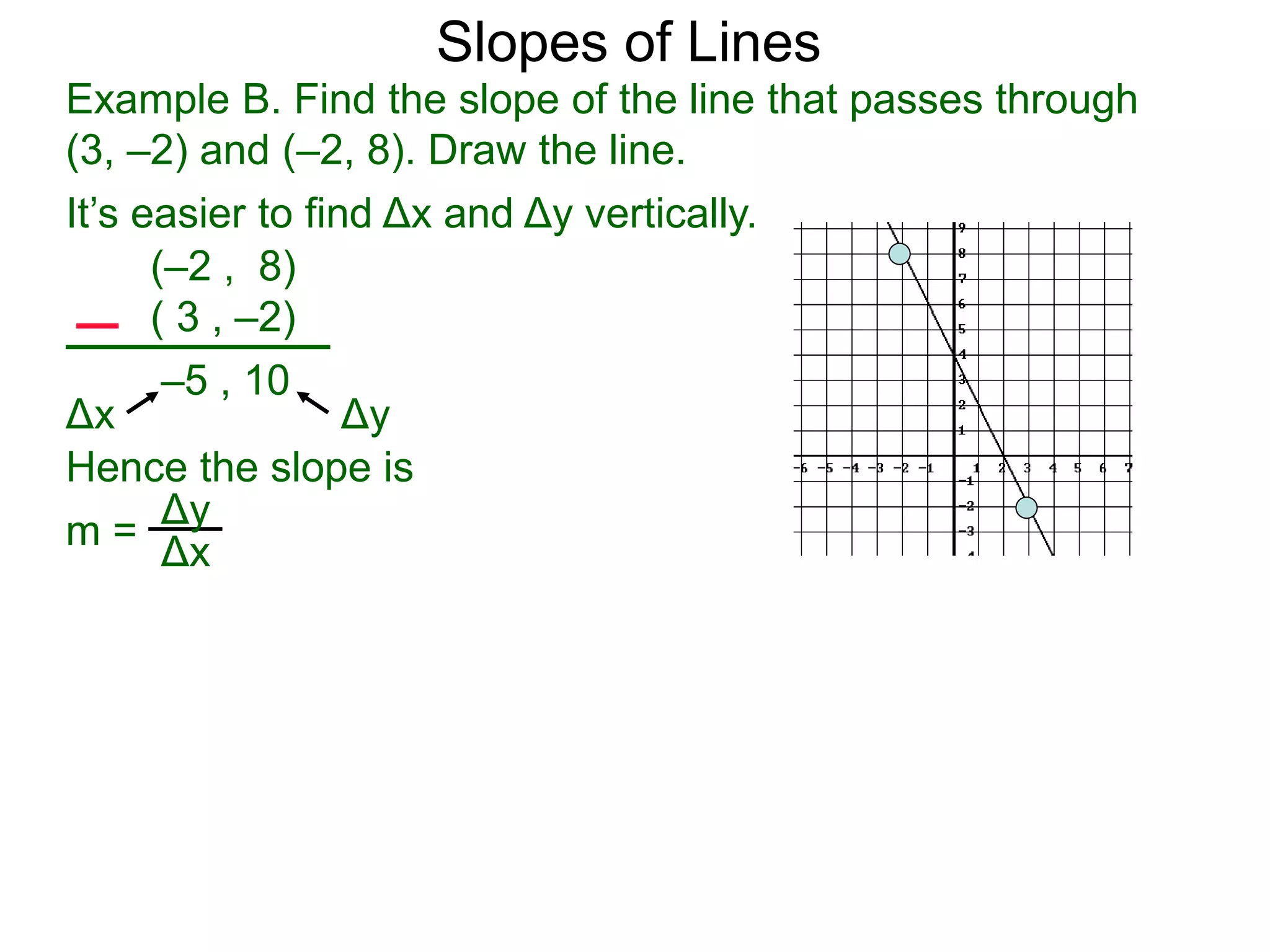
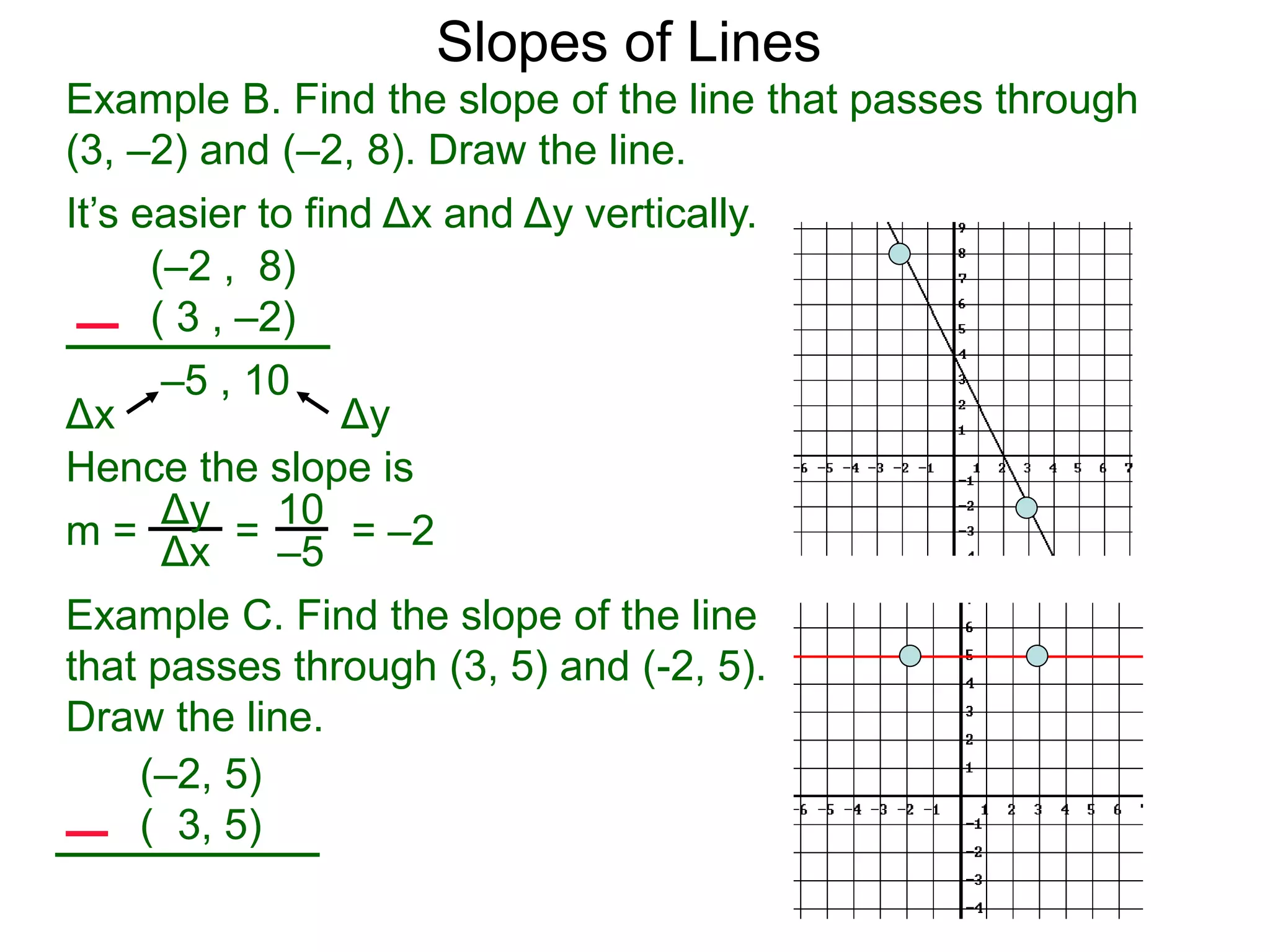
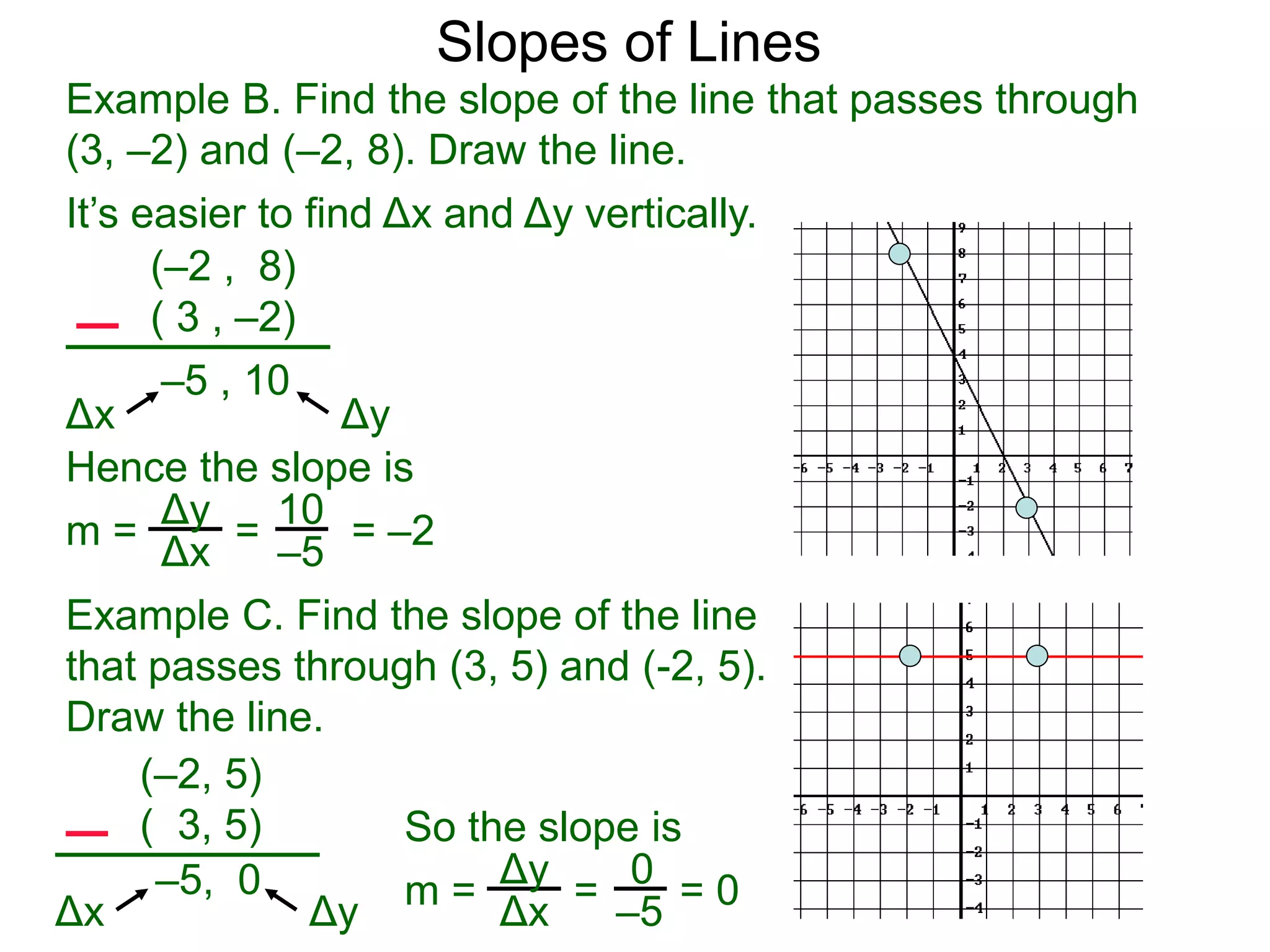
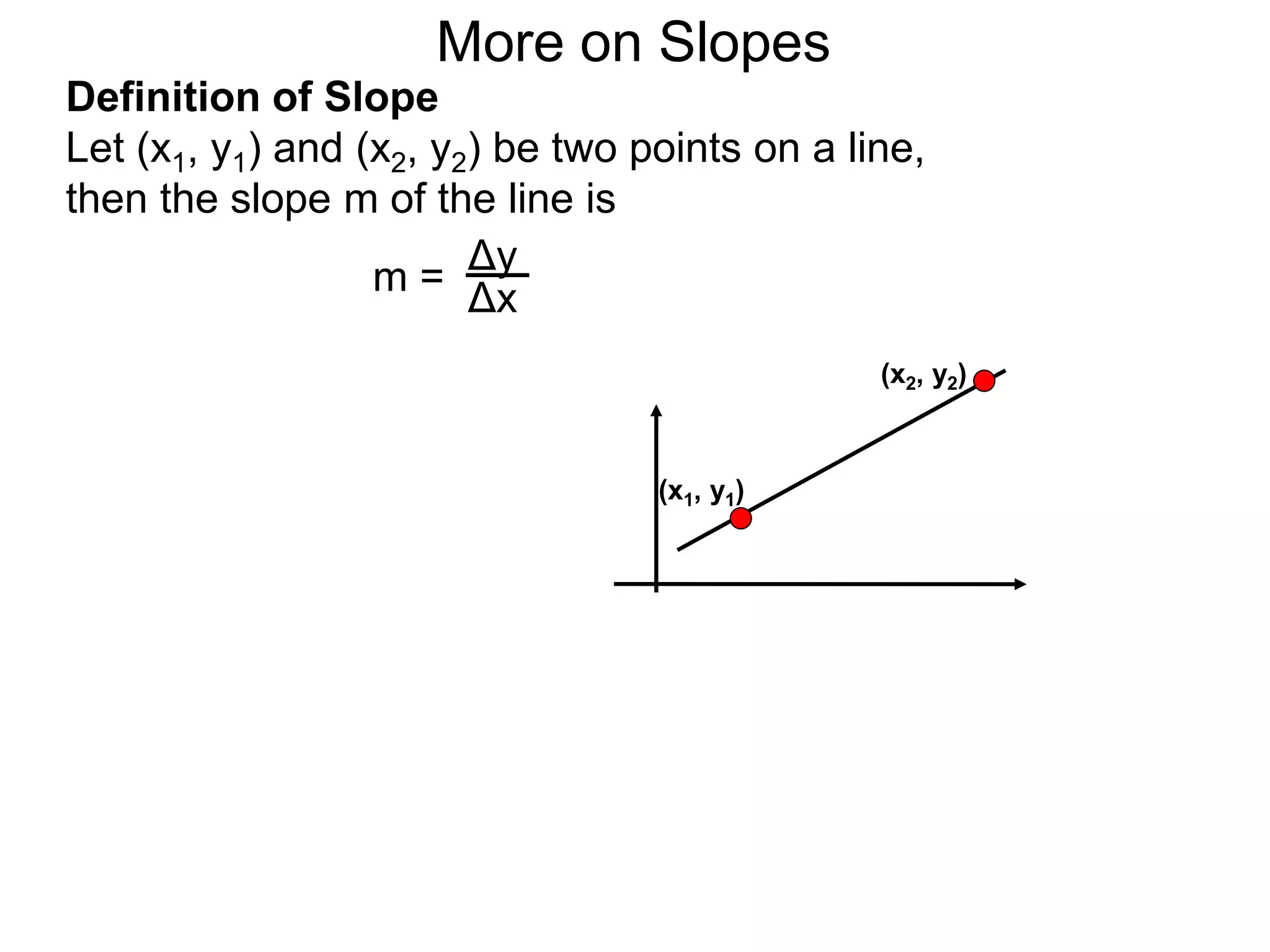
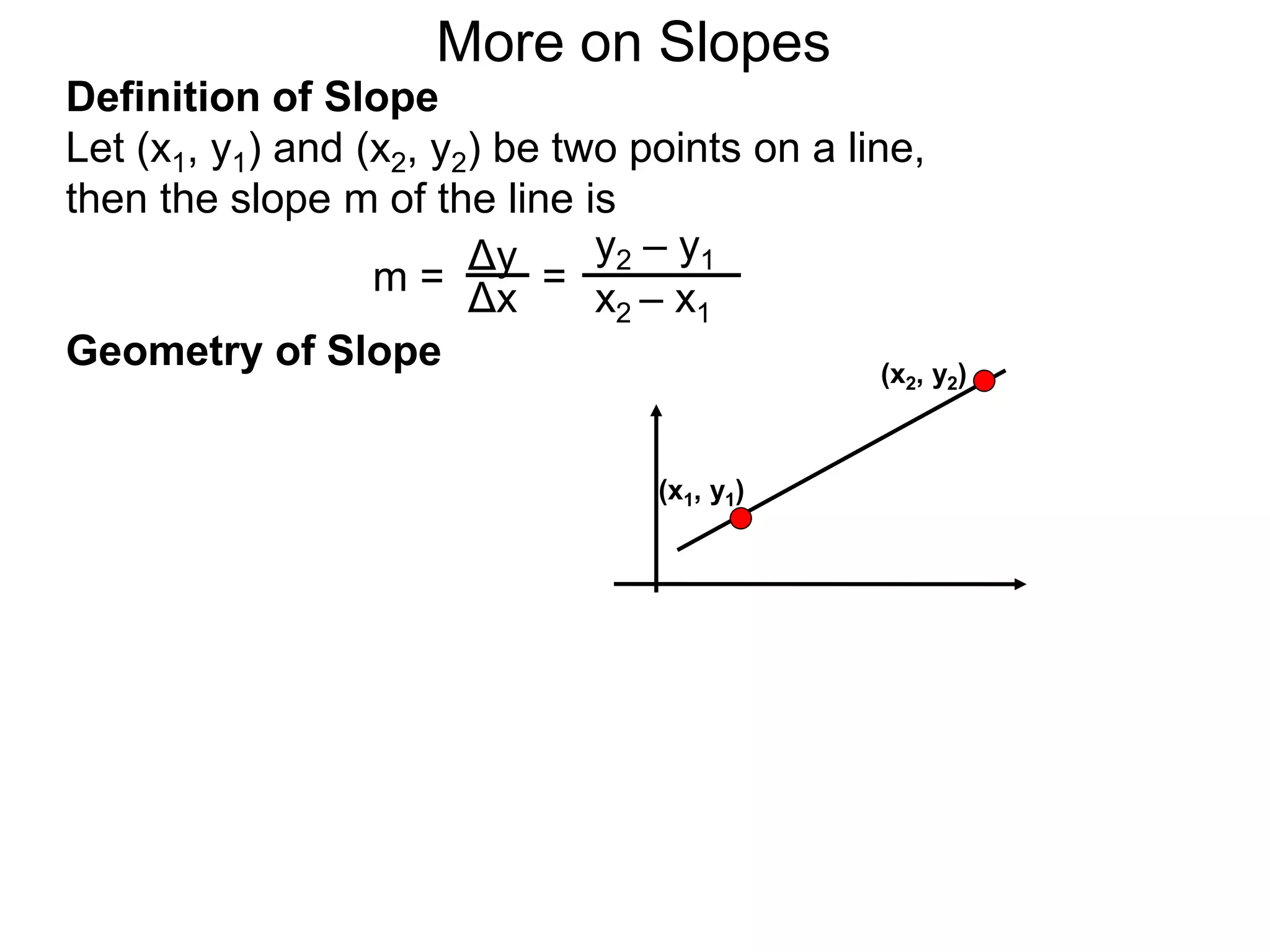
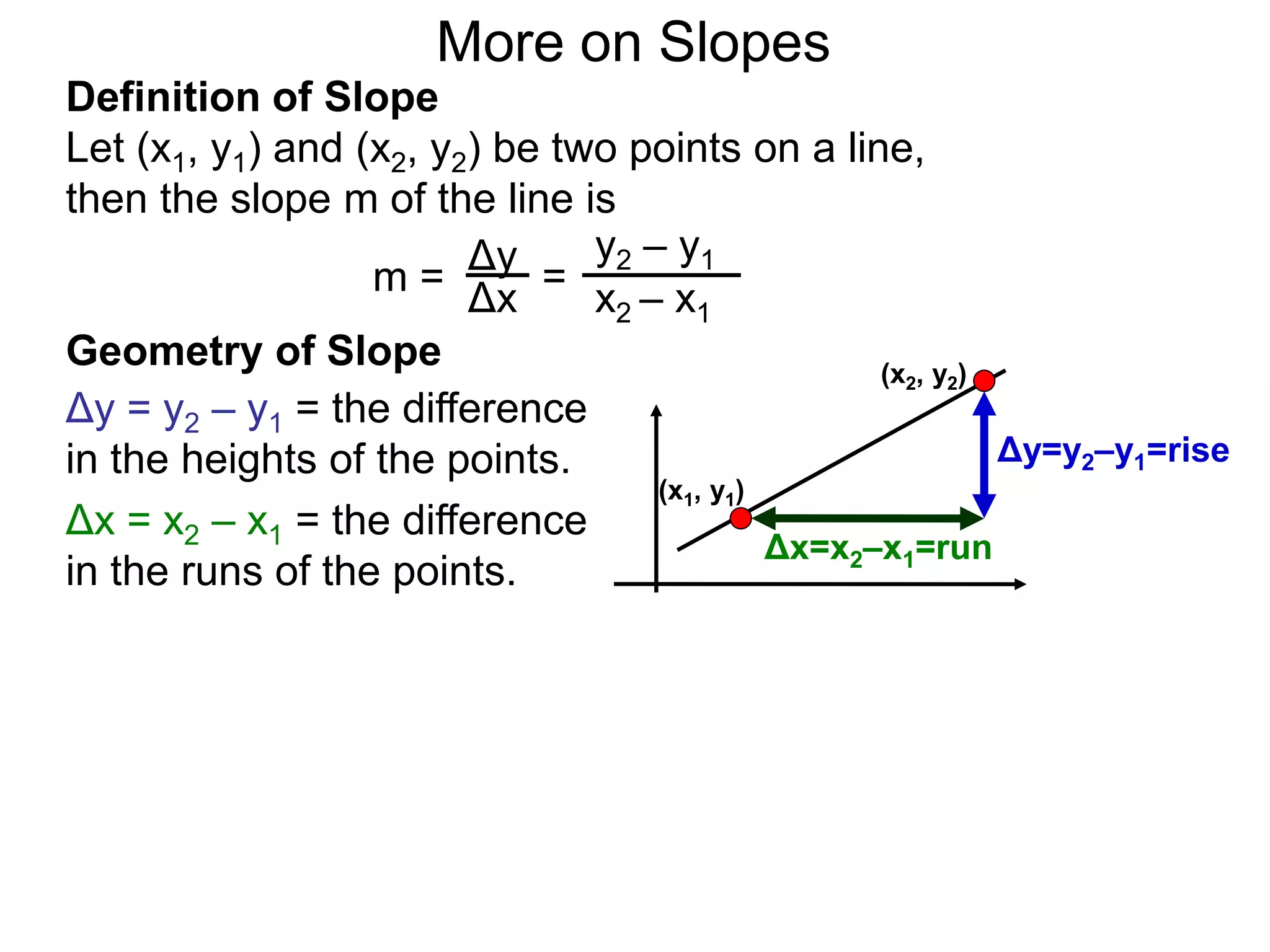
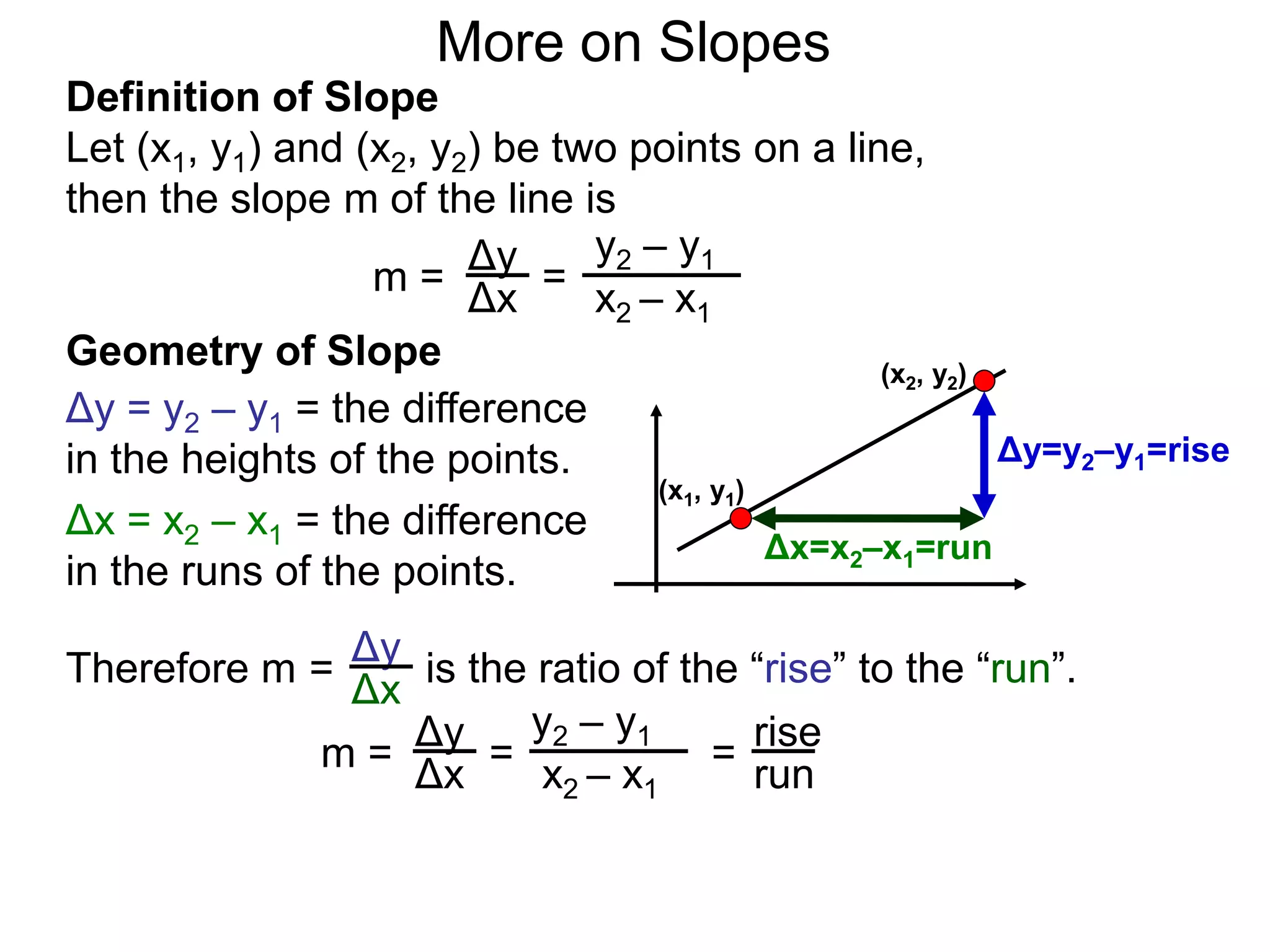
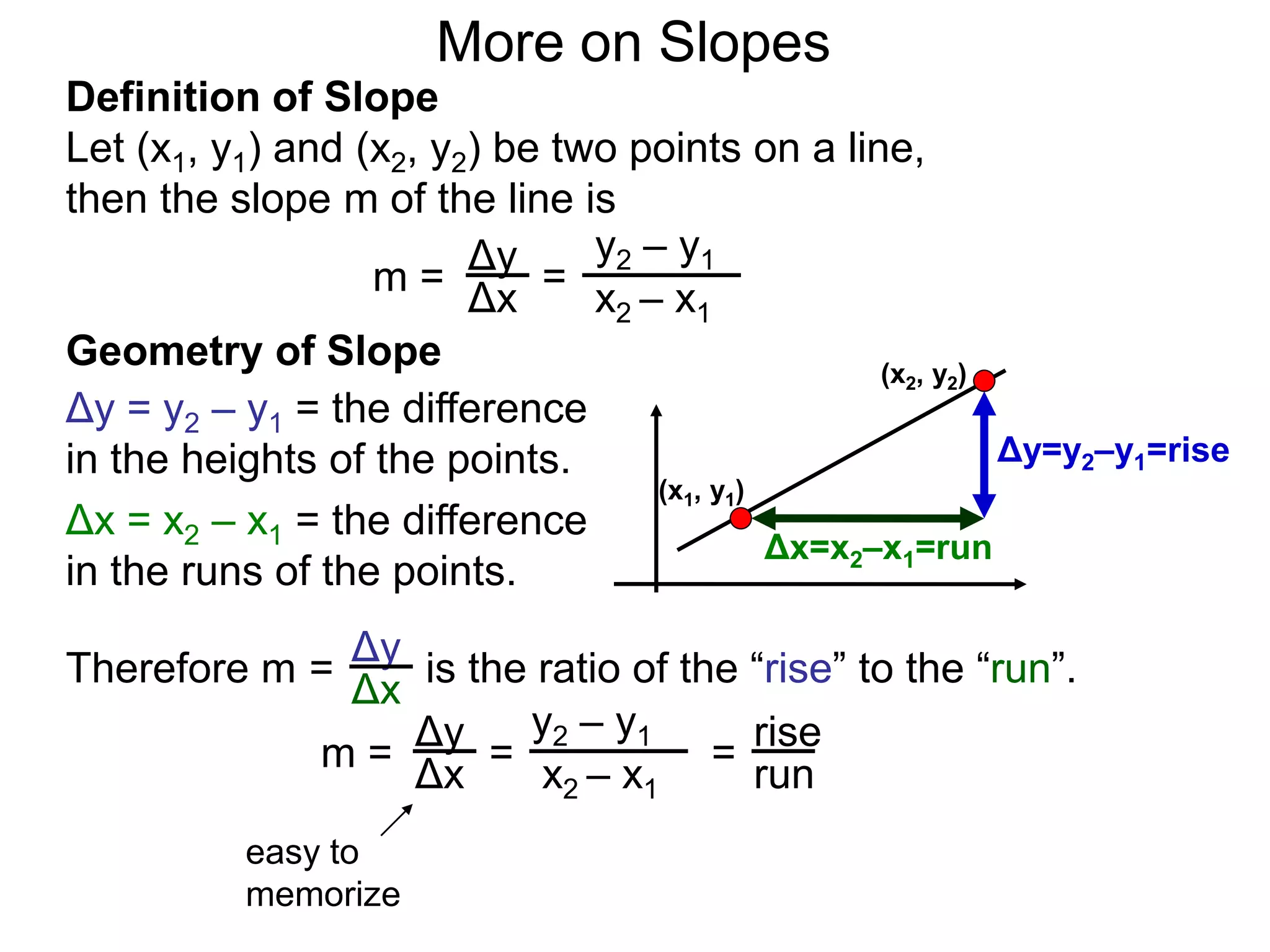
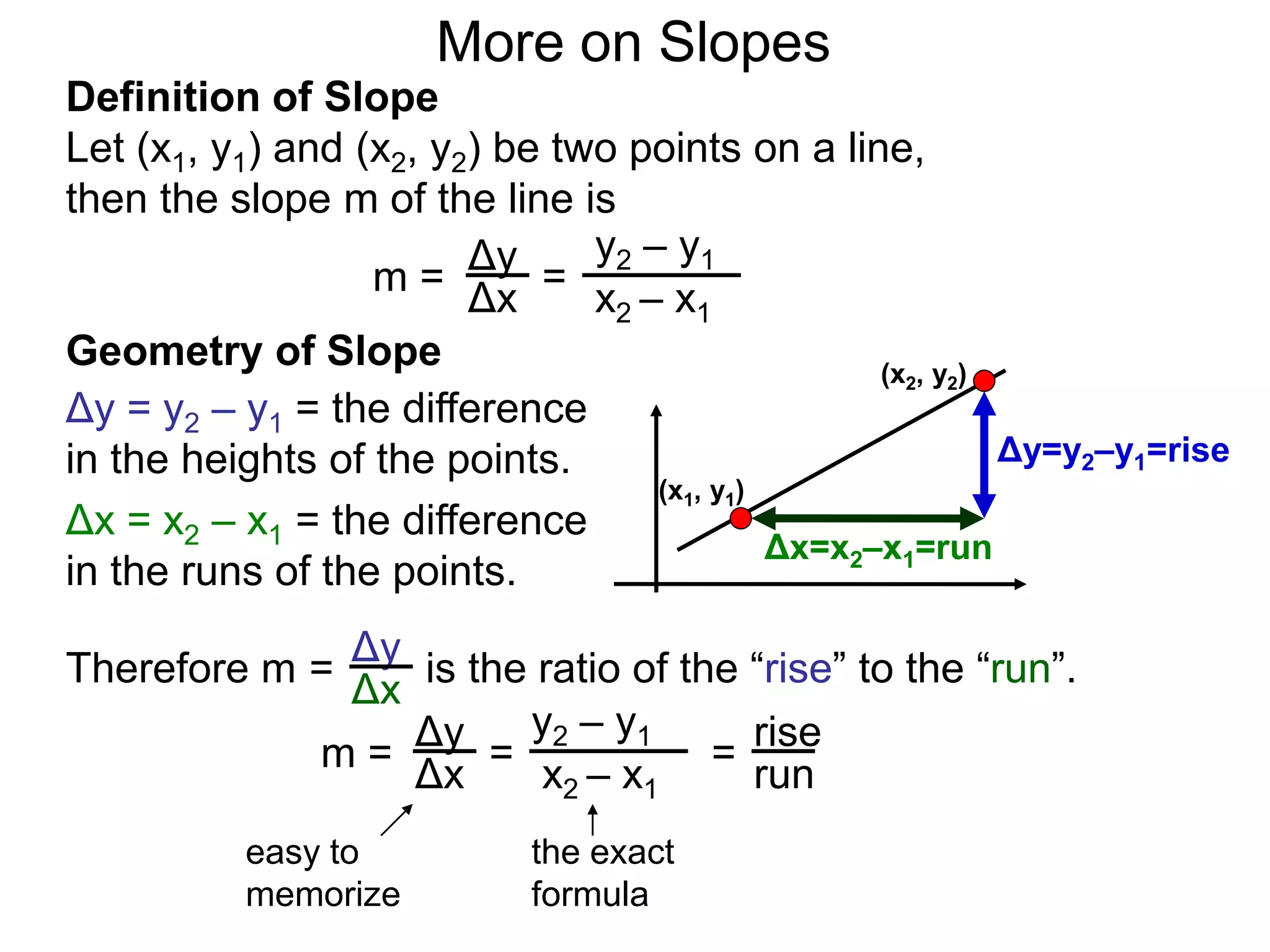
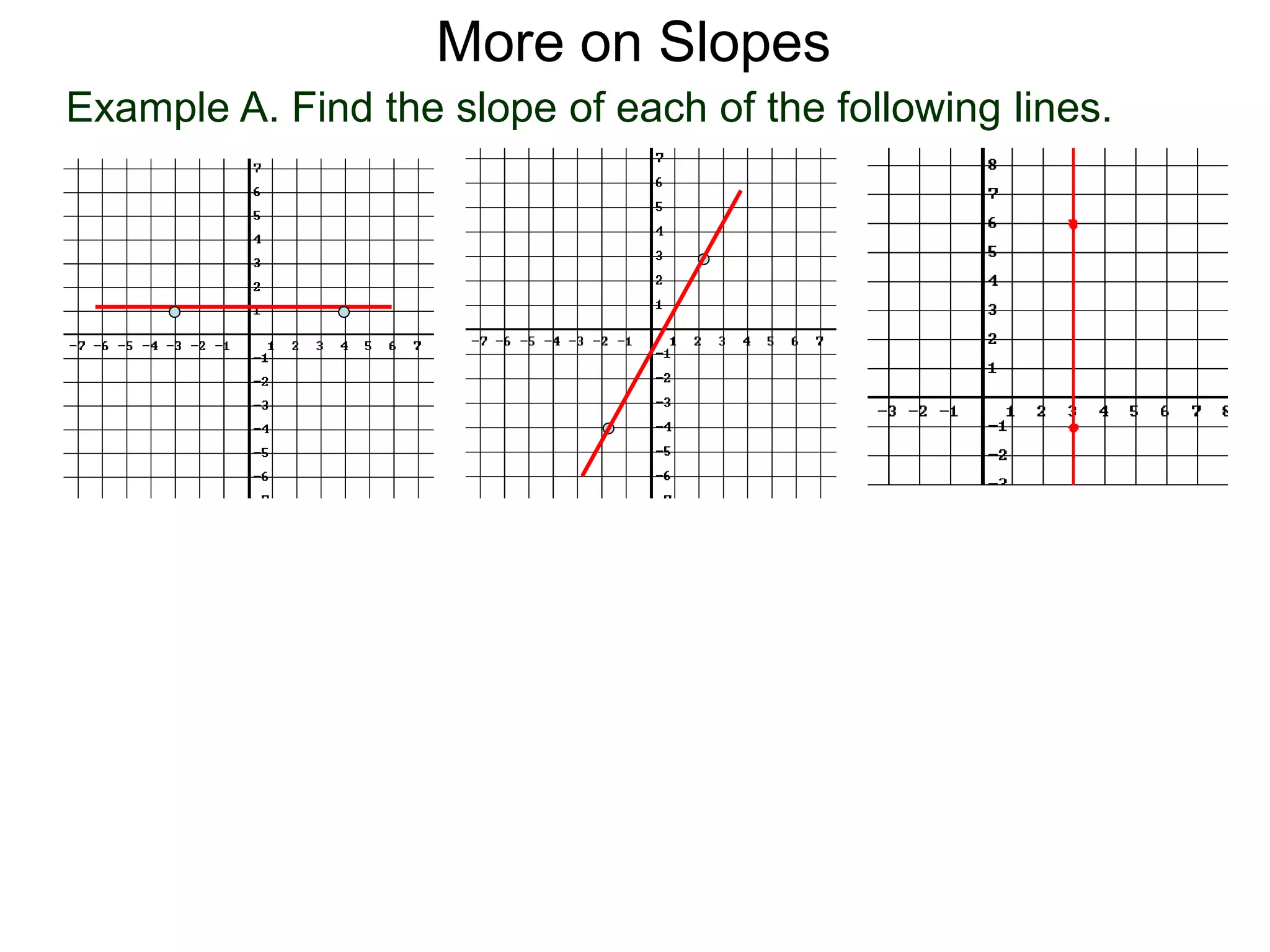
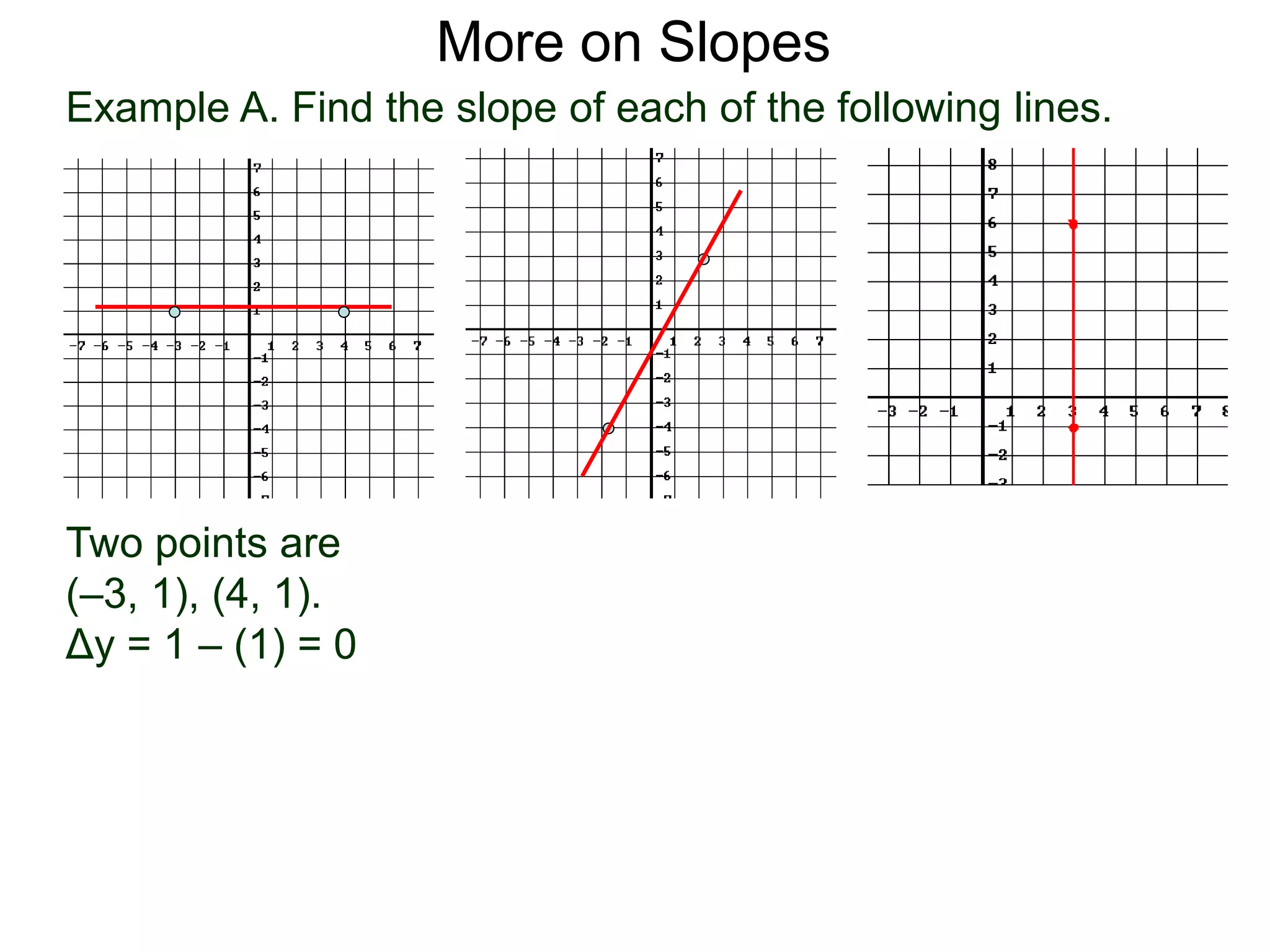
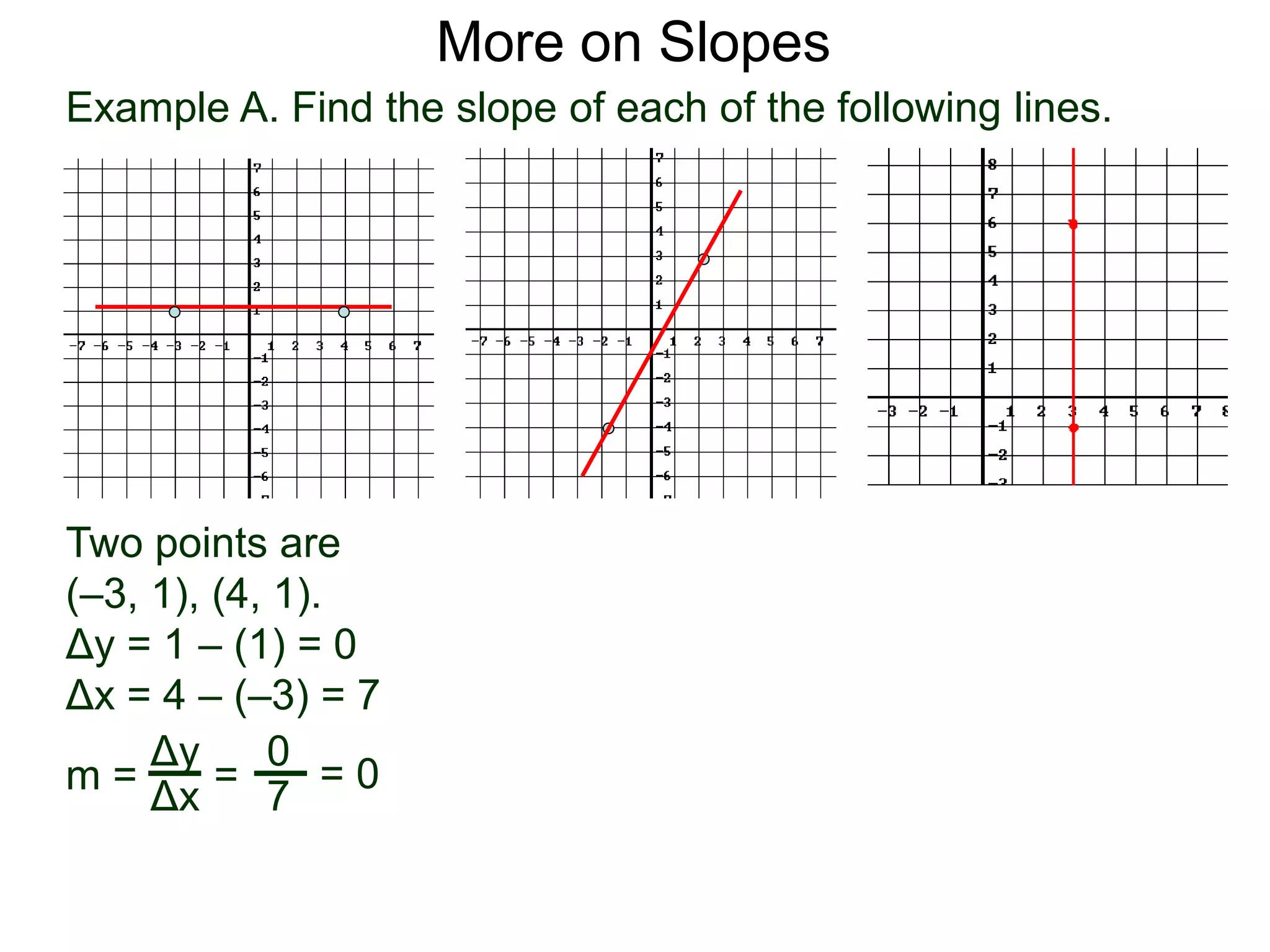
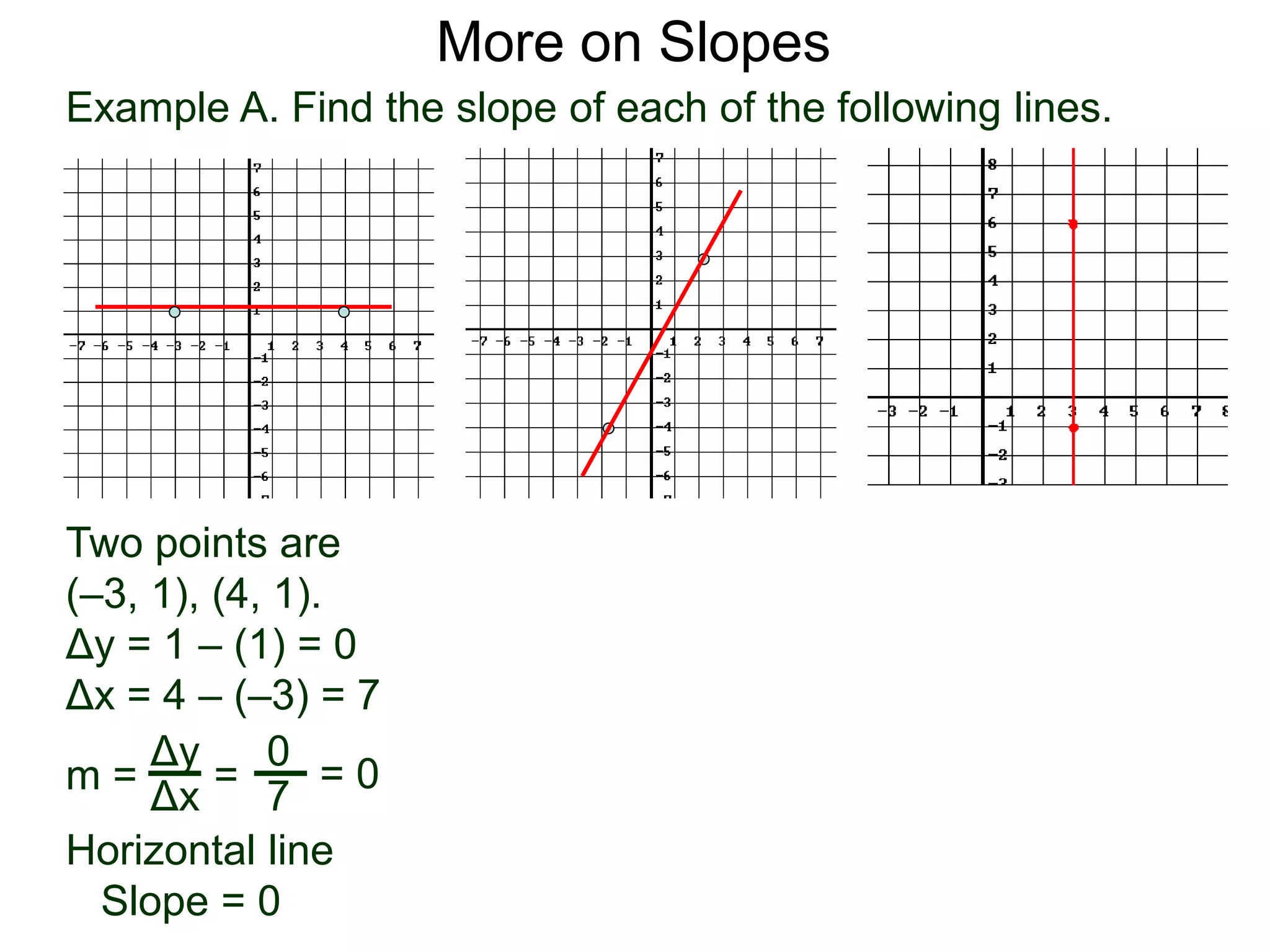
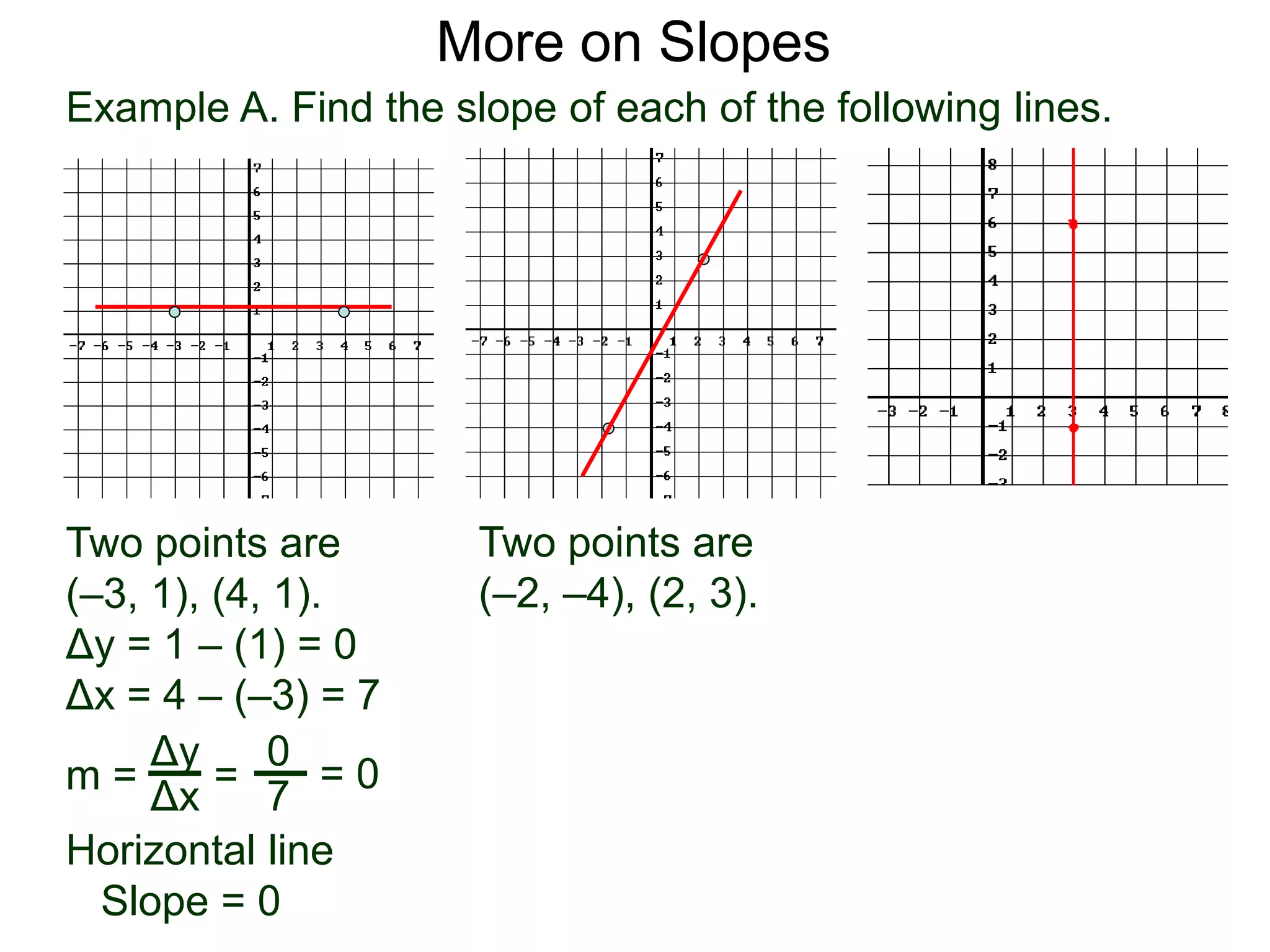
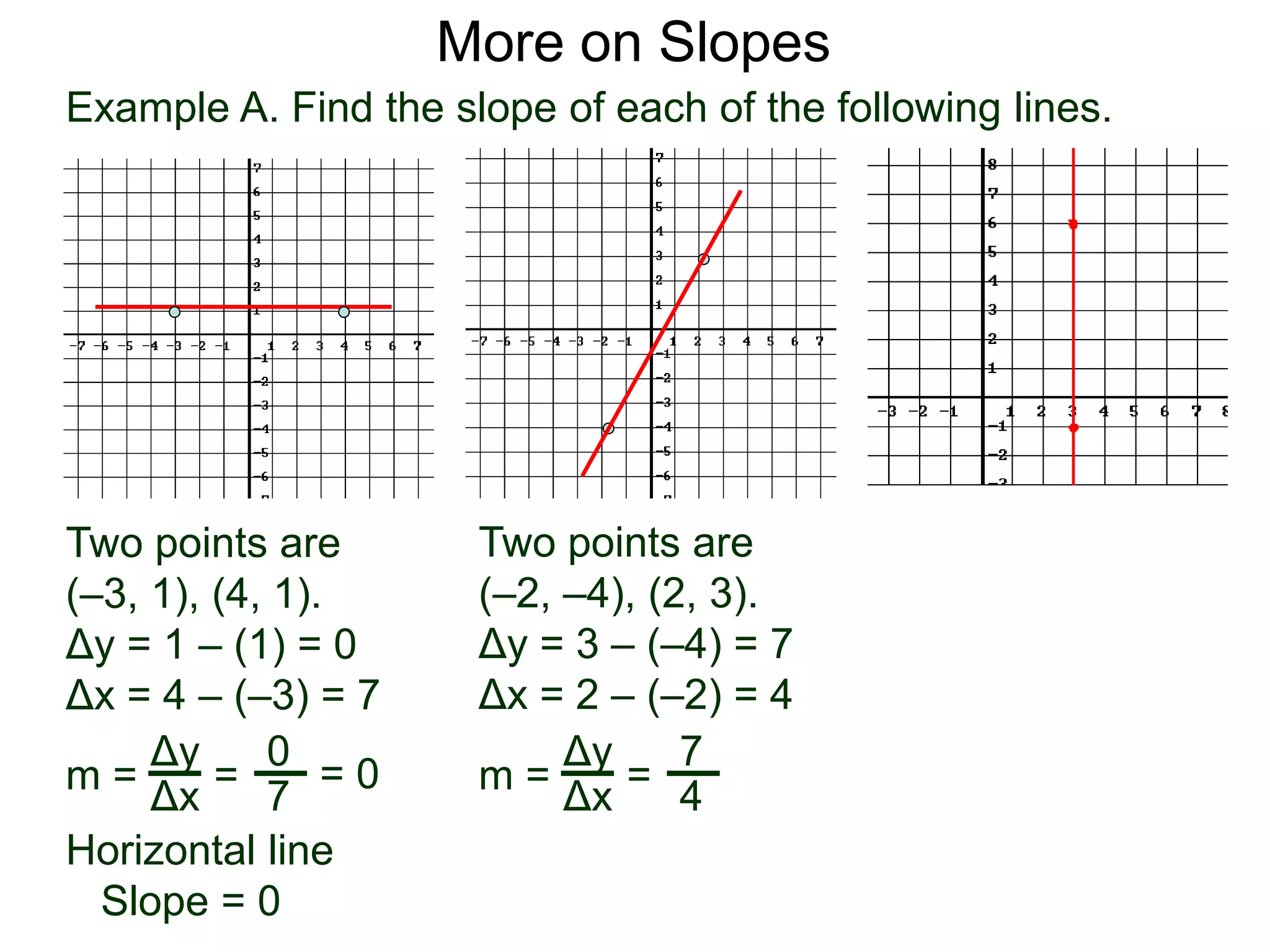
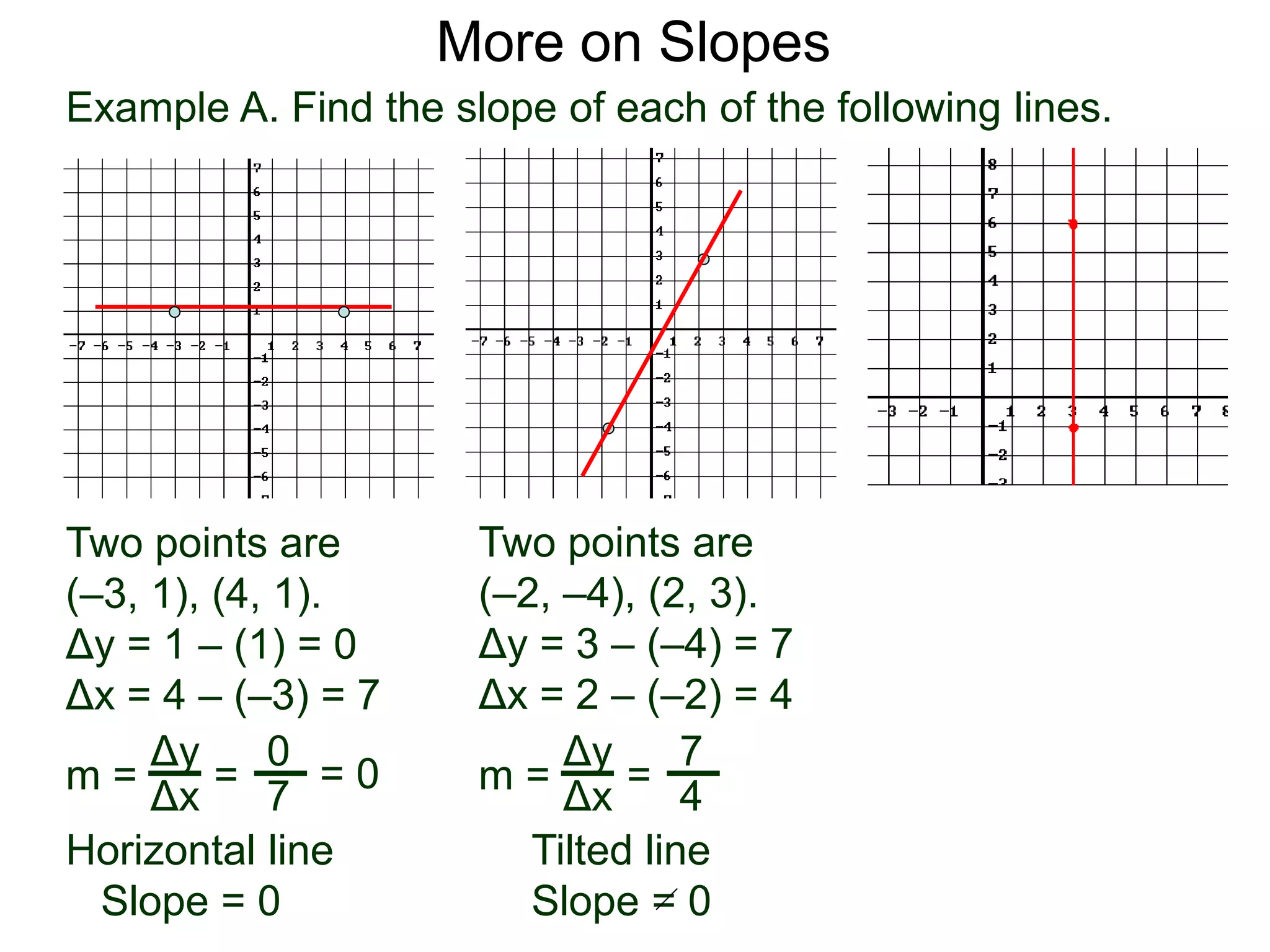
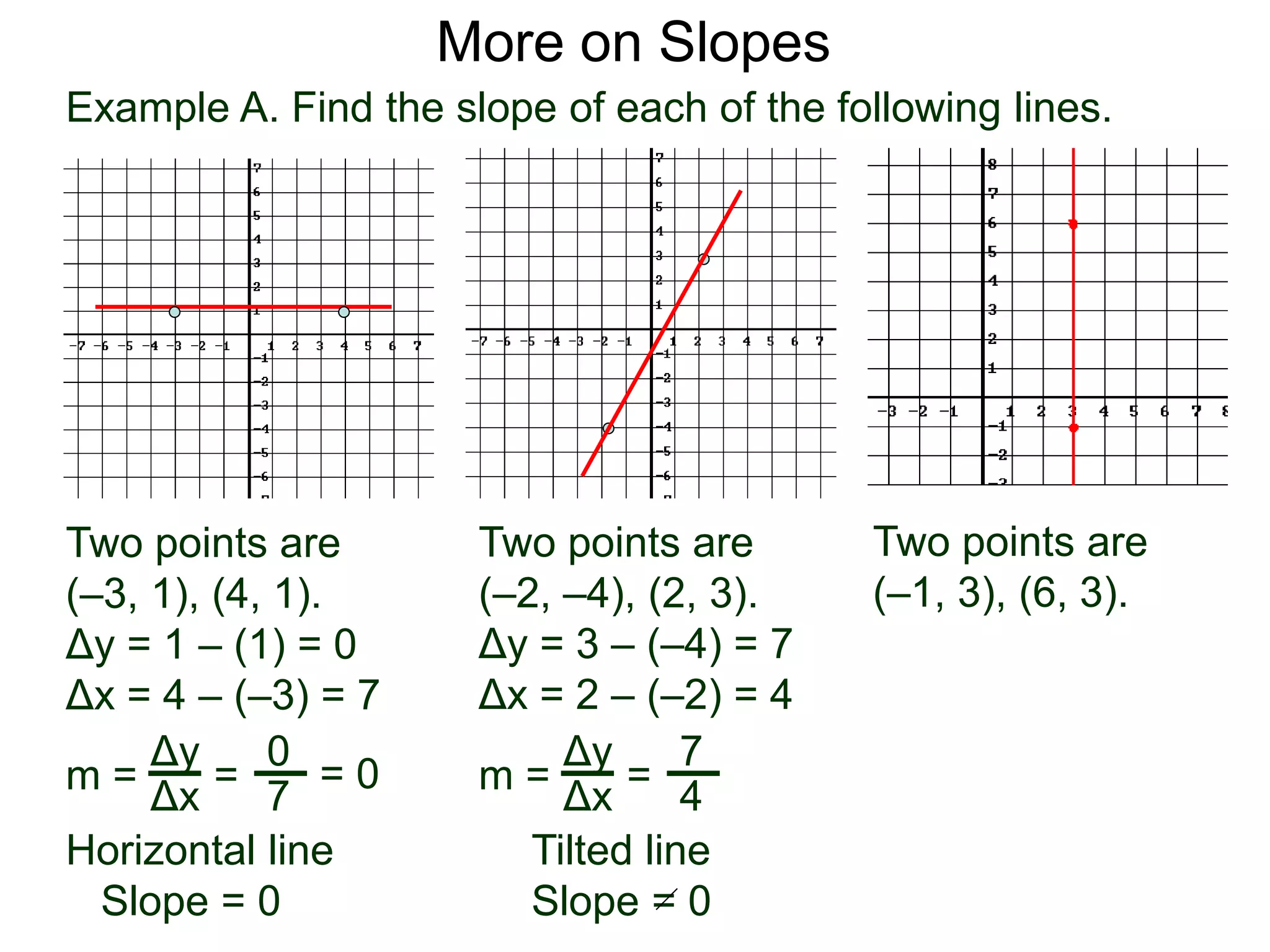
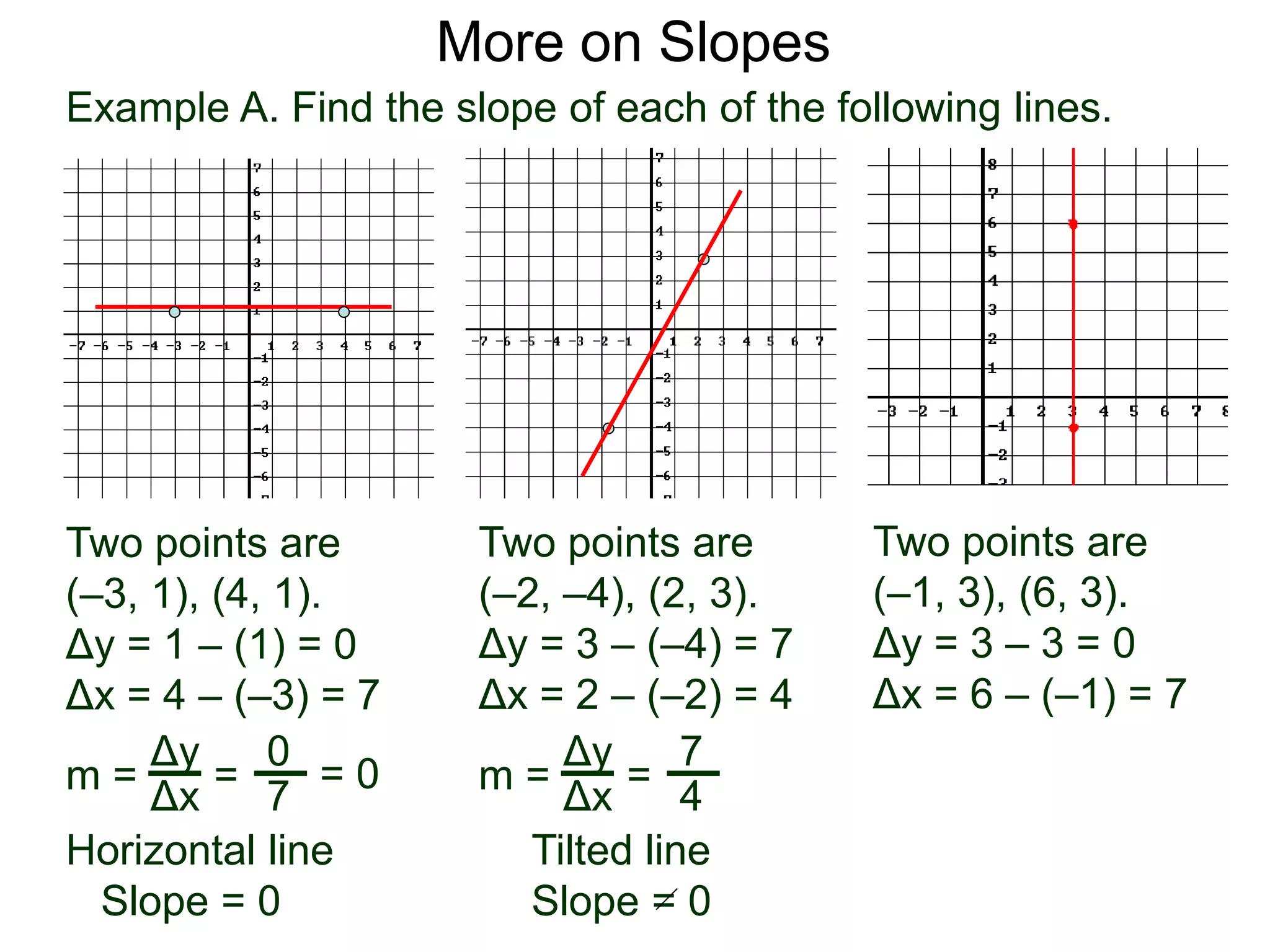
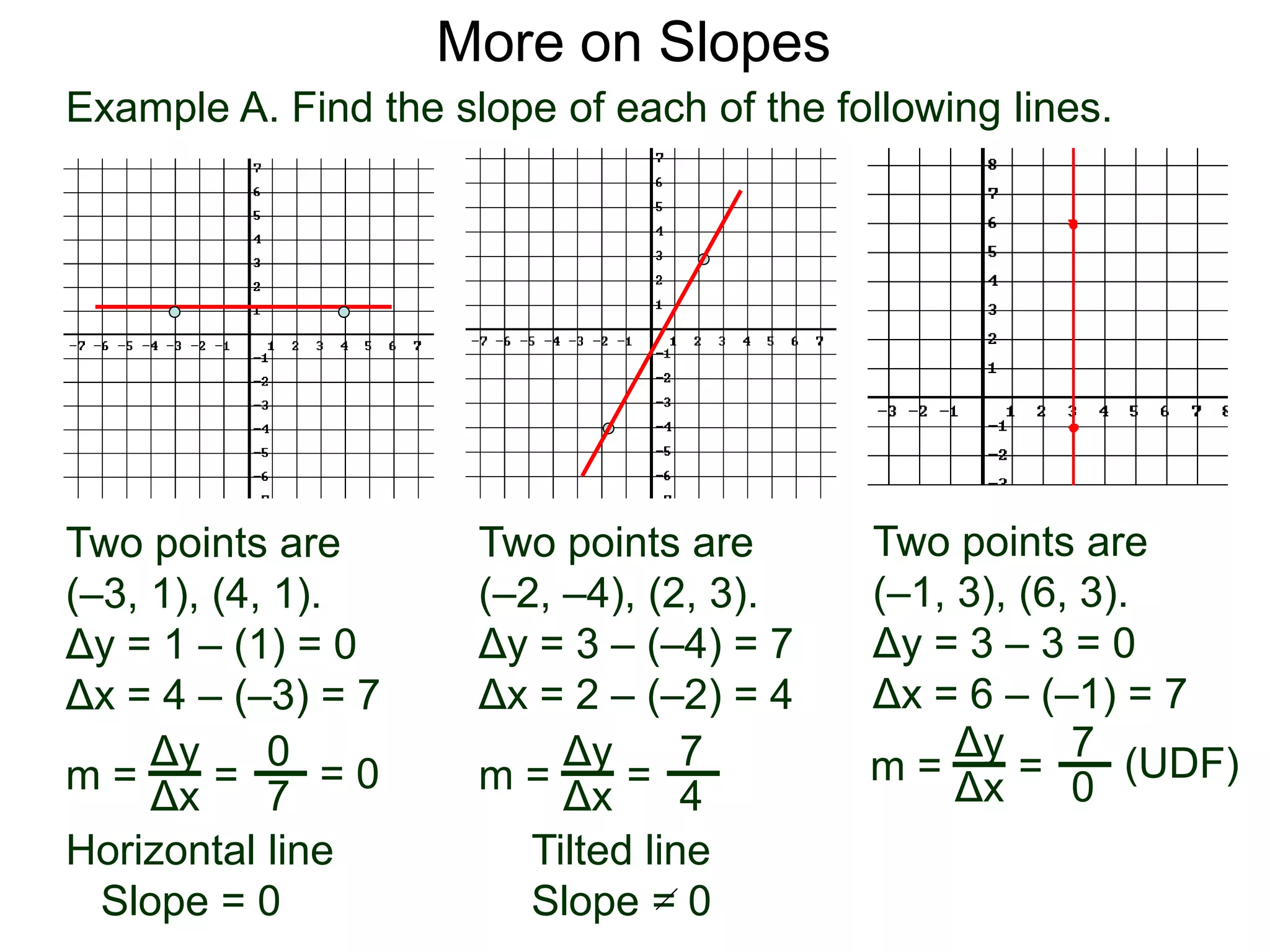
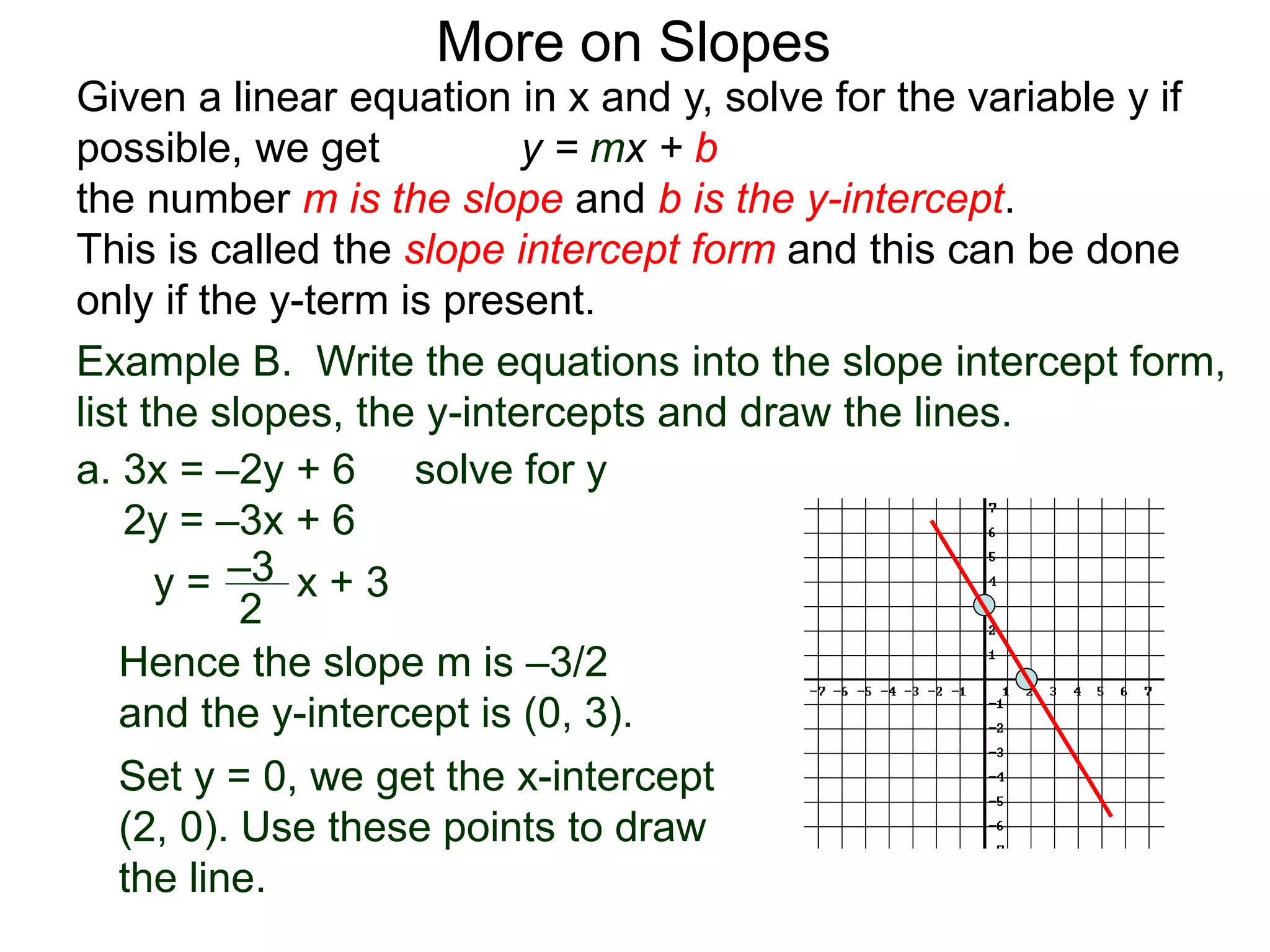
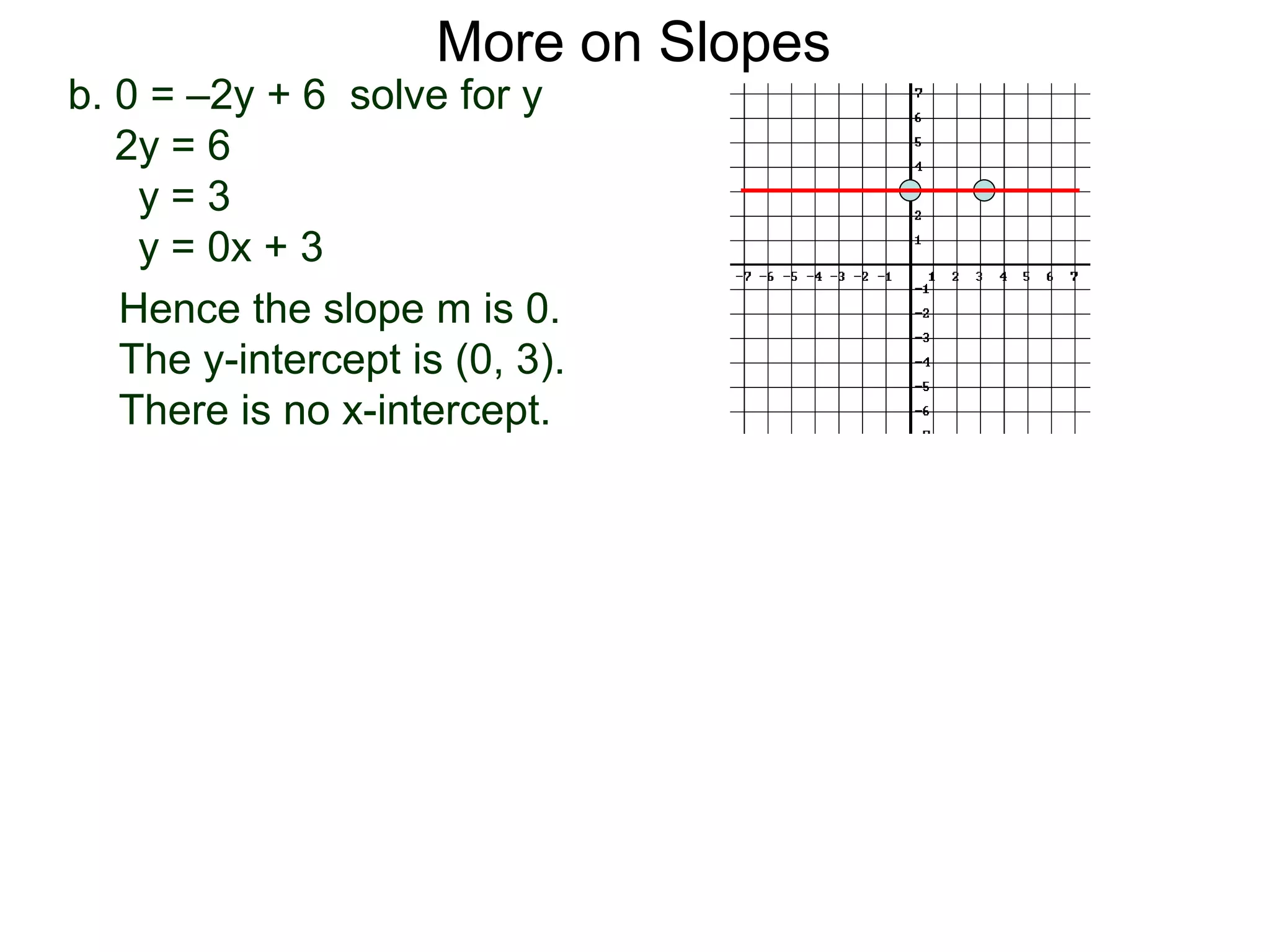
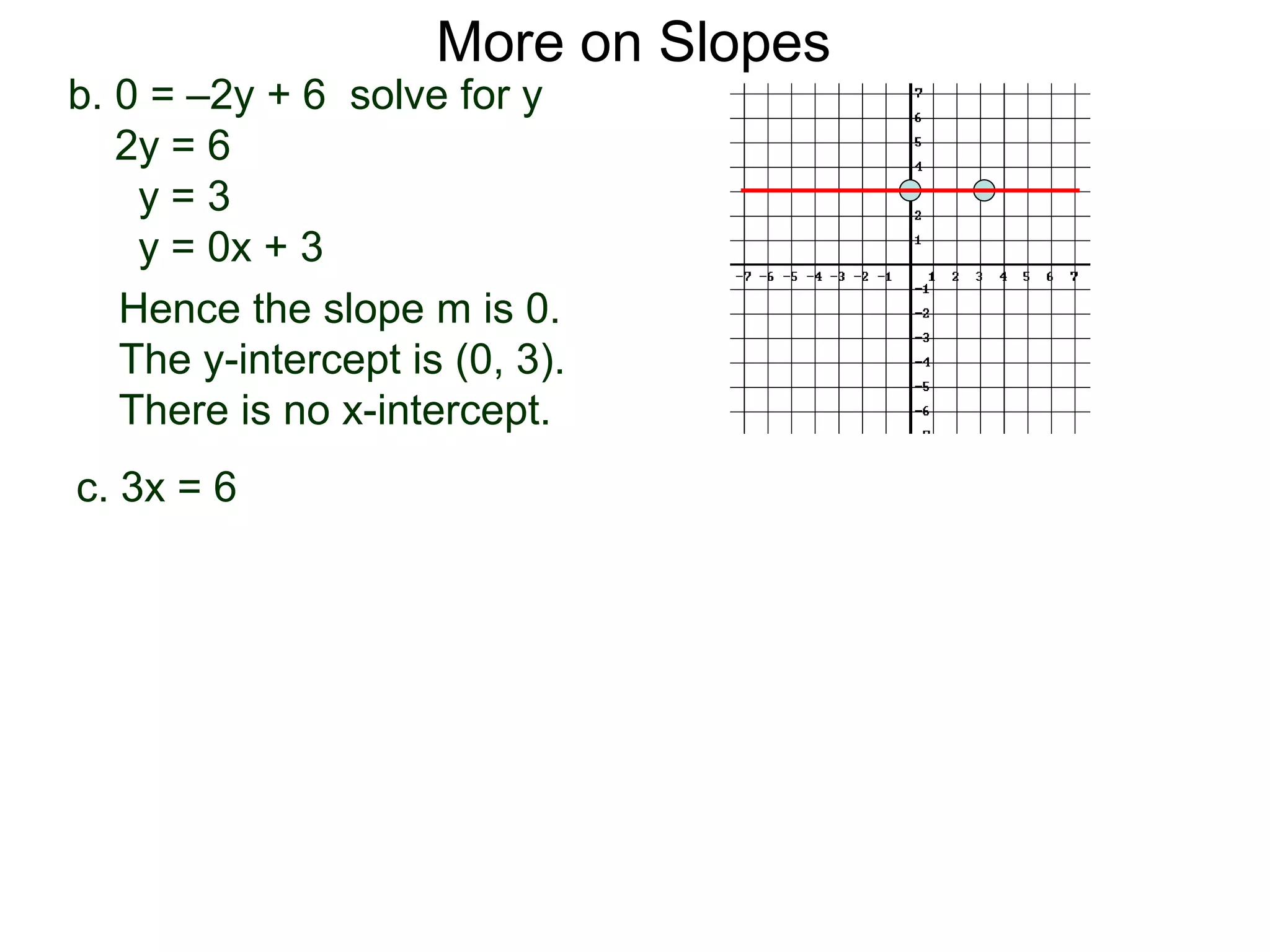
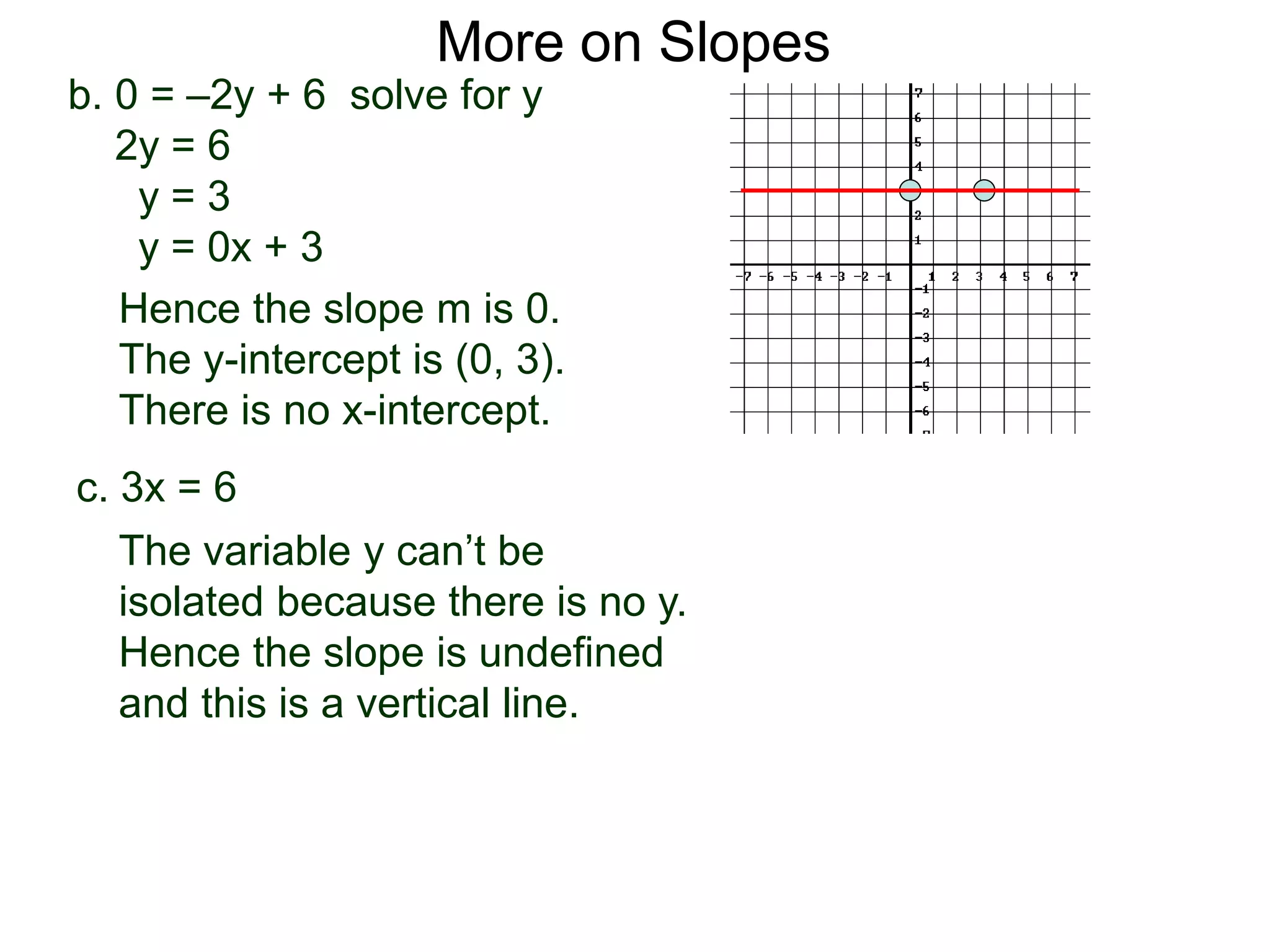
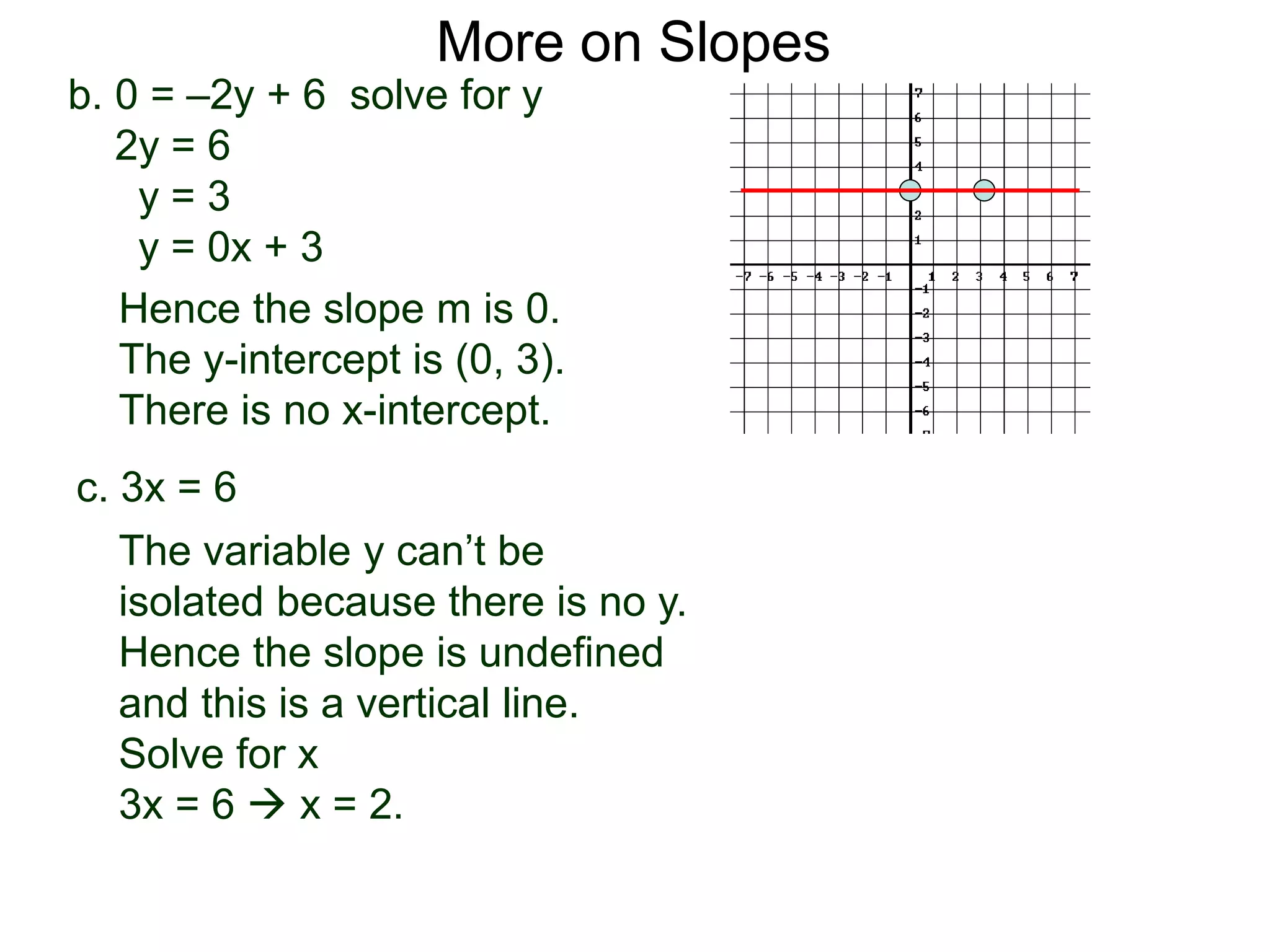
The document discusses the concept of slope of a line. It defines slope as the ratio of the "rise" over the "run" between two points on a line. Specifically: - The slope of a line is calculated as the change in the y-values (rise) divided by the change in the x-values (run) between two points on the line. - This formula is easy to memorize and captures the geometric meaning of slope as the tilt of the line. - An example problem demonstrates calculating the slope of a line between two points by finding the difference in their x- and y-values.

1. Slopes of Lines

2. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.

3. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

4. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value
Definition of Slope

5. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

6. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

7. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

8. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

9. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

10. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

11. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
then Δ x = x2 – x1
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

12. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
then Δ x = x2 – x1 = –4 – 7 = –11
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

13. Definition of Slope
Slopes of Lines

14. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
Slopes of Lines
(x1, y1)
(x2, y2)

15. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
m =
Slopes of Lines
(x1, y1)
(x2, y2)

16. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)

17. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
Geometry of Slope
(x1, y1)
(x2, y2)

18. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.

19. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.

20. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.

21. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=

22. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize

23. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula

24. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula
geometric
meaning

25. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines

26. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines

27. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

28. (–2 , 8)
( 3 , –2)
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

29. (–2 , 8)
( 3 , –2)
–5 , 10
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

30. Δy
(–2 , 8)
( 3 , –2)
–5 , 10
Δx
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

31. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m =

32. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2

33. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.

34. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.

35. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
(–2, 5)
( 3, 5)

36. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx

37. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx
So the slope is
Δx
Δy
m =

38. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx
So the slope is
Δx
Δy 0
–5
m = = = 0

39. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines

40. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.

41. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.

42. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx

43. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =

44. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!

45. As shown in example F, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!
As shown in example G, the slope of a vertical line is
undefined.

46. More on Slopes

47. Definition of Slope
More on Slopes

48. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
(x1, y1)
(x2, y2)
More on Slopes

49. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
m =
(x1, y1)
(x2, y2)
More on Slopes

50. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
(x1, y1)
(x2, y2)
More on Slopes

51. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Geometry of Slope
(x1, y1)
(x2, y2)
More on Slopes

52. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
More on Slopes

53. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
More on Slopes

54. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
More on Slopes

55. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
More on Slopes

56. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
More on Slopes

57. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula
More on Slopes

58. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run=
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m =
Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula
geometric
meaning
More on Slopes

59. Example A. Find the slope of each of the following lines.
More on Slopes

60. Example A. Find the slope of each of the following lines.
Two points are
(–3, 1), (4, 1).
More on Slopes

61. Example A. Find the slope of each of the following lines.
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
More on Slopes

62. Example A. Find the slope of each of the following lines.
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes

63. Example A. Find the slope of each of the following lines.
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
m =
Δy
Δx
=
0
7
= 0

64. Example A. Find the slope of each of the following lines.
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
= 0

65. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
= 0

66. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
= 0

67. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
= 0

68. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
= 0

69. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
Tilted line
Slope = 0
= 0

70. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
Two points are
(–1, 3), (6, 3).
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
Tilted line
Slope = 0
= 0

71. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
Two points are
(–1, 3), (6, 3).
Δy = 3 – 3 = 0
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
Tilted line
Slope = 0
= 0

72. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
Two points are
(–1, 3), (6, 3).
Δy = 3 – 3 = 0
Δx = 6 – (–1) = 7
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
Horizontal line
Slope = 0
Tilted line
Slope = 0
= 0

73. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
Two points are
(–1, 3), (6, 3).
Δy = 3 – 3 = 0
Δx = 6 – (–1) = 7
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
m =
Δy
Δx
=
7
0
Horizontal line
Slope = 0
Tilted line
Slope = 0
= 0 (UDF)

74. Example A. Find the slope of each of the following lines.
Two points are
(–2, –4), (2, 3).
Δy = 3 – (–4) = 7
Δx = 2 – (–2) = 4
m =
Two points are
(–3, 1), (4, 1).
Δy = 1 – (1) = 0
Δx = 4 – (–3) = 7
Two points are
(–1, 3), (6, 3).
Δy = 3 – 3 = 0
Δx = 6 – (–1) = 7
More on Slopes
Δy
Δx
=
7
4
m =
Δy
Δx
=
0
7
m =
Δy
Δx
=
7
0
Horizontal line
Slope = 0
Vertical line
Slope is UDF
Tilted line
Slope = 0
= 0 (UDF)

75. Lines that go through the
quadrants I and III have
positive slopes.
More on Slopes

76. Lines that go through the
quadrants I and III have
positive slopes.
More on Slopes
III
III IV

77. Lines that go through the
quadrants I and III have
positive slopes.
Lines that go through the
quadrants II and IV have
negative slopes.
More on Slopes
III
III IV

78. Lines that go through the
quadrants I and III have
positive slopes.
Lines that go through the
quadrants II and IV have
negative slopes.
More on Slopes
III
III IV
III
III IV

79. Lines that go through the
quadrants I and III have
positive slopes.
Lines that go through the
quadrants II and IV have
negative slopes.
More on Slopes
The formula for slopes requires geometric information,
i.e. the positions of two points on the line.
III
III IV
III
III IV

80. Lines that go through the
quadrants I and III have
positive slopes.
Lines that go through the
quadrants II and IV have
negative slopes.
More on Slopes
The formula for slopes requires geometric information,
i.e. the positions of two points on the line.
However, if a line is given by its equation instead, we may
determine the slope from the equation directly.
III
III IV
III
III IV

81. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
More on Slopes

82. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
More on Slopes

83. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes

84. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

85. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

86. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

87. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

88. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Hence the slope m is –3/2
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

89. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Hence the slope m is –3/2
and the y-intercept is (0, 3).
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

90. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Hence the slope m is –3/2
and the y-intercept is (0, 3).
Set y = 0, we get the x-intercept
(2, 0).

91. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Hence the slope m is –3/2
and the y-intercept is (0, 3).
Set y = 0, we get the x-intercept
(2, 0). Use these points to draw
the line.
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

92. Given a linear equation in x and y, solve for the variable y if
possible, we get y = mx + b
the number m is the slope and b is the y-intercept.
This is called the slope intercept form and this can be done
only if the y-term is present.
More on Slopes
a. 3x = –2y + 6 solve for y
2y = –3x + 6
y =
2
–3 x + 3
Hence the slope m is –3/2
and the y-intercept is (0, 3).
Set y = 0, we get the x-intercept
(2, 0). Use these points to draw
the line.
Example B. Write the equations into the slope intercept form,
list the slopes, the y-intercepts and draw the lines.

93. b. 0 = –2y + 6
More on Slopes

94. b. 0 = –2y + 6 solve for y
More on Slopes

95. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
More on Slopes

96. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
More on Slopes

97. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
More on Slopes

98. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
More on Slopes

99. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
More on Slopes

100. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
More on Slopes

101. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes

102. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes
The variable y can’t be
isolated because there is no y.

103. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes
The variable y can’t be
isolated because there is no y.
Hence the slope is undefined
and this is a vertical line.

104. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes
The variable y can’t be
isolated because there is no y.
Hence the slope is undefined
and this is a vertical line.
Solve for x
3x = 6  x = 2.

105. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes
The variable y can’t be
isolated because there is no y.
Hence the slope is undefined
and this is a vertical line.
Solve for x
3x = 6  x = 2.
This is the vertical line x = 2.

106. b. 0 = –2y + 6 solve for y
2y = 6
y = 3
y = 0x + 3
Hence the slope m is 0.
The y-intercept is (0, 3).
There is no x-intercept.
c. 3x = 6
More on Slopes
The variable y can’t be
isolated because there is no y.
Hence the slope is undefined
and this is a vertical line.
Solve for x
3x = 6  x = 2.
This is the vertical line x = 2.

107. Two Facts About Slopes
I. Parallel lines have the same slope.
More on Slopes

108. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
More on Slopes

109. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
More on Slopes

110. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
More on Slopes

111. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
More on Slopes

112. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
More on Slopes

113. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
More on Slopes

114. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes

115. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes
b. What is the slope of L if L is perpendicular to 3x = 2y + 4?

116. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes
b. What is the slope of L if L is perpendicular to 3x = 2y + 4?
Solve for y to find the slope of 3x – 4 = 2y

117. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes
b. What is the slope of L if L is perpendicular to 3x = 2y + 4?
Solve for y to find the slope of 3x – 4 = 2y
x – 2 = y2
3

118. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes
b. What is the slope of L if L is perpendicular to 3x = 2y + 4?
Solve for y to find the slope of 3x – 4 = 2y
x – 2 = y
Hence the slope of 3x = 2y + 4 is .
2
3
2
3

119. Two Facts About Slopes
I. Parallel lines have the same slope.
II. Slopes of perpendicular lines are the negative reciprocal of
each other.
Example C.
a. The line L is parallel to 4x – 2y = 5, what is the slope of L?
Solve for y for 4x – 2y = 5
4x – 5 = 2y
2x – 5/2 = y
So the slope of 4x – 2y = 5 is 2.
Since L is parallel to it , so L has slope 2 also.
More on Slopes
b. What is the slope of L if L is perpendicular to 3x = 2y + 4?
Solve for y to find the slope of 3x – 4 = 2y
x – 2 = y
Hence the slope of 3x = 2y + 4 is .
So L has slope –2/3 since L is perpendicular to it.
2
3
2
3

120. Summary on Slopes
How to Find Slopes
I. If two points on the line are given, use the slope formula
II. If the equation of the line is given, solve for the y and get
slope intercept form y = mx + b, then the number m is
the slope.
Geometry of Slope
The slope of tilted lines are nonzero.
Lines with positive slopes connect quadrants I and III.
Lines with negative slopes connect quadrants II and IV.
Lines that have slopes with large absolute values are steep.
The slope of a horizontal line is 0.
A vertical lines does not have slope or that it’s UDF.
Parallel lines have the same slopes.
Perpendicular lines have the negative reciprocal slopes of
each other.
rise
run=m =
Δy
Δx
y2 – y1
x2 – x1
=

121. Exercise A. Identify the vertical and the horizontal lines by
inspection first. Find their slopes or if it’s undefined, state so.
Fine the slopes of the other ones by solving for the y.
1. x – y = 3 2. 2x = 6 3. –y – 7= 0
4. 0 = 8 – 2x 5. y = –x + 4 6. 2x/3 – 3 = 6/5
7. 2x = 6 – 2y 8. 4y/5 – 12 = 3x/4 9. 2x + 3y = 3
10. –6 = 3x – 2y 11. 3x + 2 = 4y + 3x 12. 5x/4 + 2y/3 = 2
Exercise B.
13–18. Select two points and estimate the slope of each line.
13. 14. 15.
More on Slopes

122. 16. 17. 18.
Exercise C. Draw and find the slope of the line that passes
through the given two points. Identify the vertical line and the
horizontal lines by inspection first.
19. (0, –1), (–2, 1) 20. (1, –2), (–2, 0) 21. (1, –2), (–2, –1)
22. (3, –1), (3, 1) 23. (1, –2), (–2, 3) 24. (2, –1), (3, –1)
25. (4, –2), (–3, 1) 26. (4, –2), (4, 0) 27. (7, –2), (–2, –6)
28. (3/2, –1), (3/2, 1) 29. (3/2, –1), (1, –3/2)
30. (–5/2, –1/2), (1/2, 1) 31. (3/2, 1/3), (1/3, 1/3)
32. (–2/3, –1/4), (1/2, 2/3) 33. (3/4, –1/3), (1/3, 3/2)
More on Slopes

123. Exercise D.
34. Identify which lines are parallel and which one are
perpendicular.
A. The line that passes through (0, 1), (1, –2)
D. 2x – 4y = 1
B. C.
E. The line that’s perpendicular to 3y = x
F. The line with the x–intercept at 3 and y intercept at 6.
Find the slope, if possible of each of the following lines.
35. The line passes with the x intercept at x = 2,
and y–intercept at y = –5.
More on Slopes

124. 36. The equation of the line is 3x = –5y+7
37. The equation of the line is 0 = –5y+7
38. The equation of the line is 3x = 7
39. The line is parallel to 2y = 5 – 6x
40. the line is perpendicular to 2y = 5 – 6x
41. The line is parallel to the line in problem 30.
42. the line is perpendicular to line in problem 31.
43. The line is parallel to the line in problem 33.
44. the line is perpendicular to line in problem 34.
More on Slopes
Find the slope, if possible of each of the following lines

125. Summary of Slope
The slope of the line that passes through (x1, y1) and (x2, y2) is
Horizontal line
Slope = 0
Vertical line
Slope is UDF.
Tilted line
Slope = –2  0
rise
run
=m =
Δy
Δx
y2 – y1
x2 – x1
=

126. Exercise A.
Select two points and estimate the slope of each line.
1. 2. 3. 4.
Slopes of Lines
5. 6. 7. 8.

127. Exercise B. Draw and find the slope of the line that passes
through the given two points. Identify the vertical line and the
horizontal lines by inspection first.
9. (0, –1), (–2, 1) 10. (1, –2), (–2, 0) 11. (1, –2), (–2, –1)
12. (3, –1), (3, 1) 13. (1, –2), (–2, 3) 14. (2, –1), (3, –1)
15. (4, –2), (–3, 1) 16. (4, –2), (4, 0) 17. (7, –2), (–2, –6)
18. (3/2, –1), (3/2, 1) 19. (3/2, –1), (1, –3/2)
20. (–5/2, –1/2), (1/2, 1) 21. (3/2, 1/3), (1/3, 1/3)
22. (–2/3, –1/4), (1/2, 2/3) 23. (3/4, –1/3), (1/3, 3/2)
Slopes of Lines