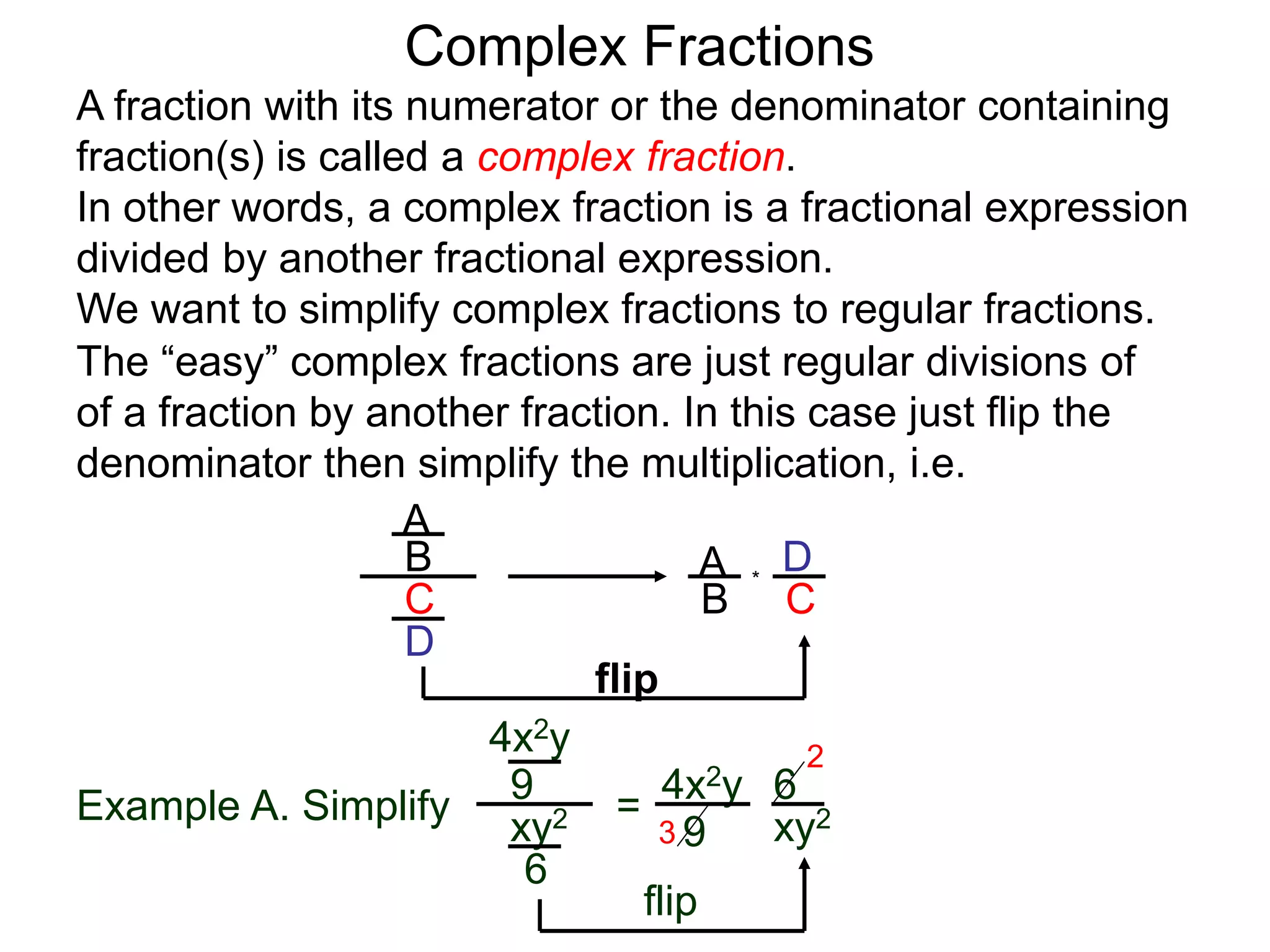
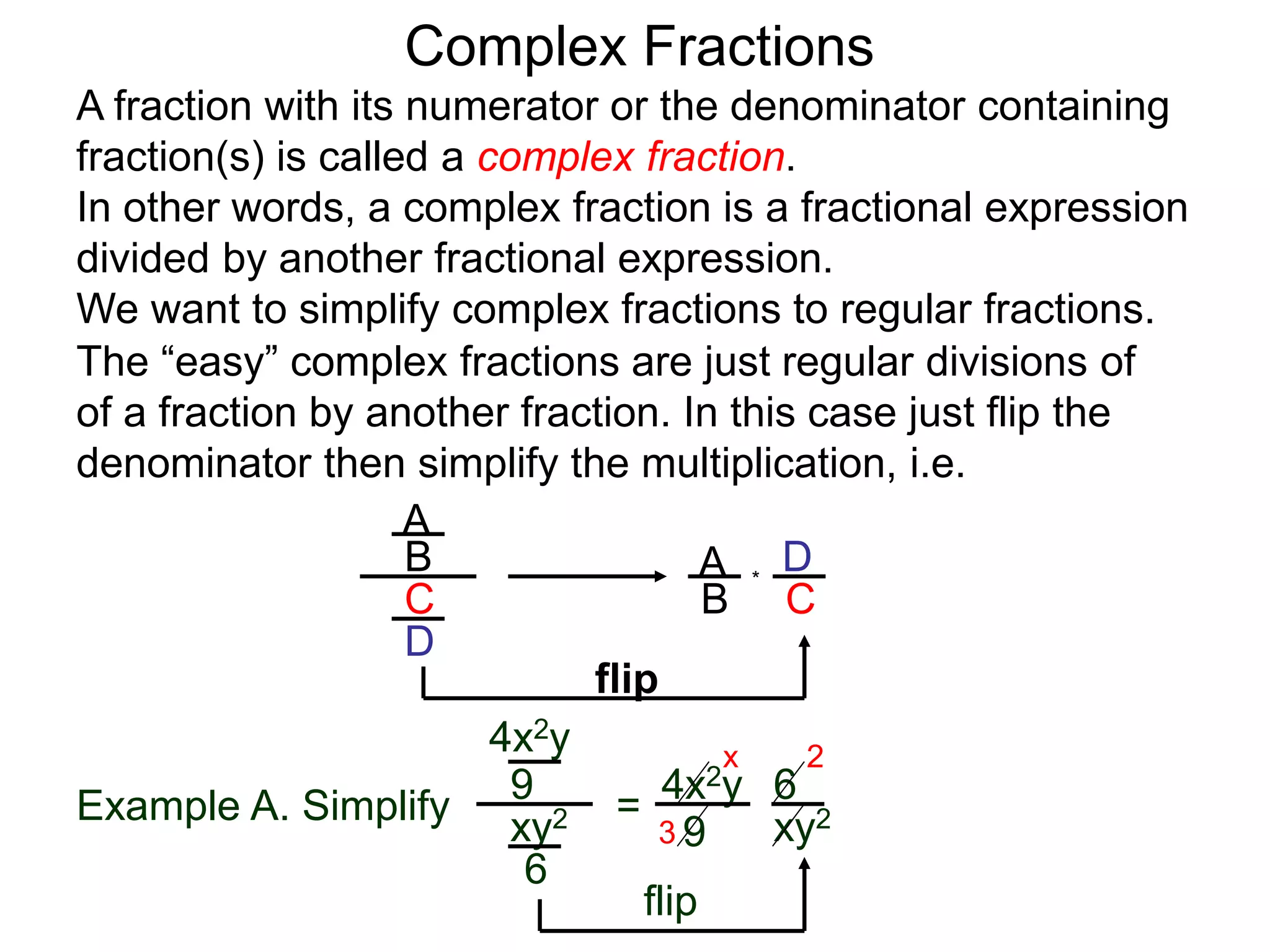
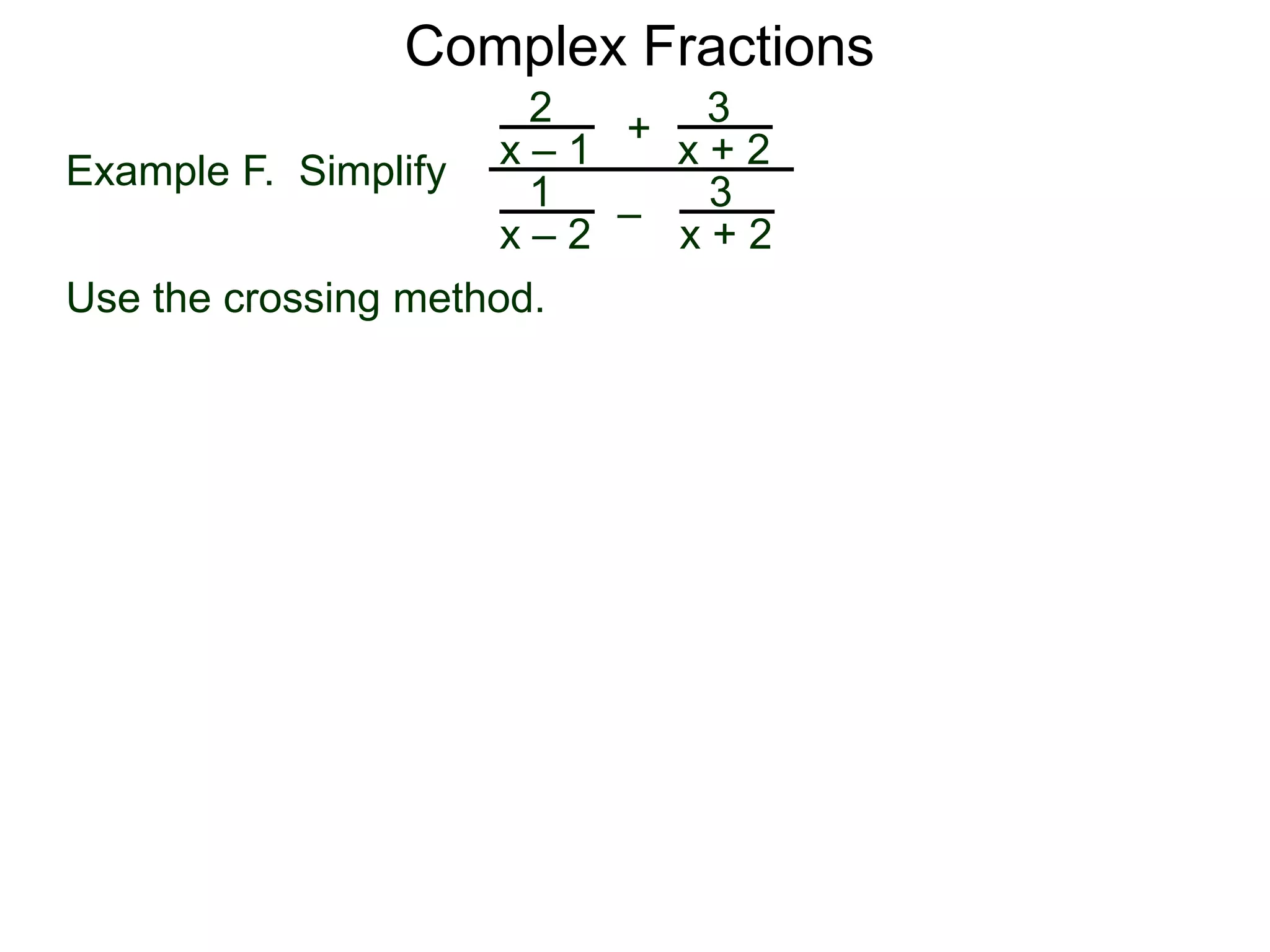
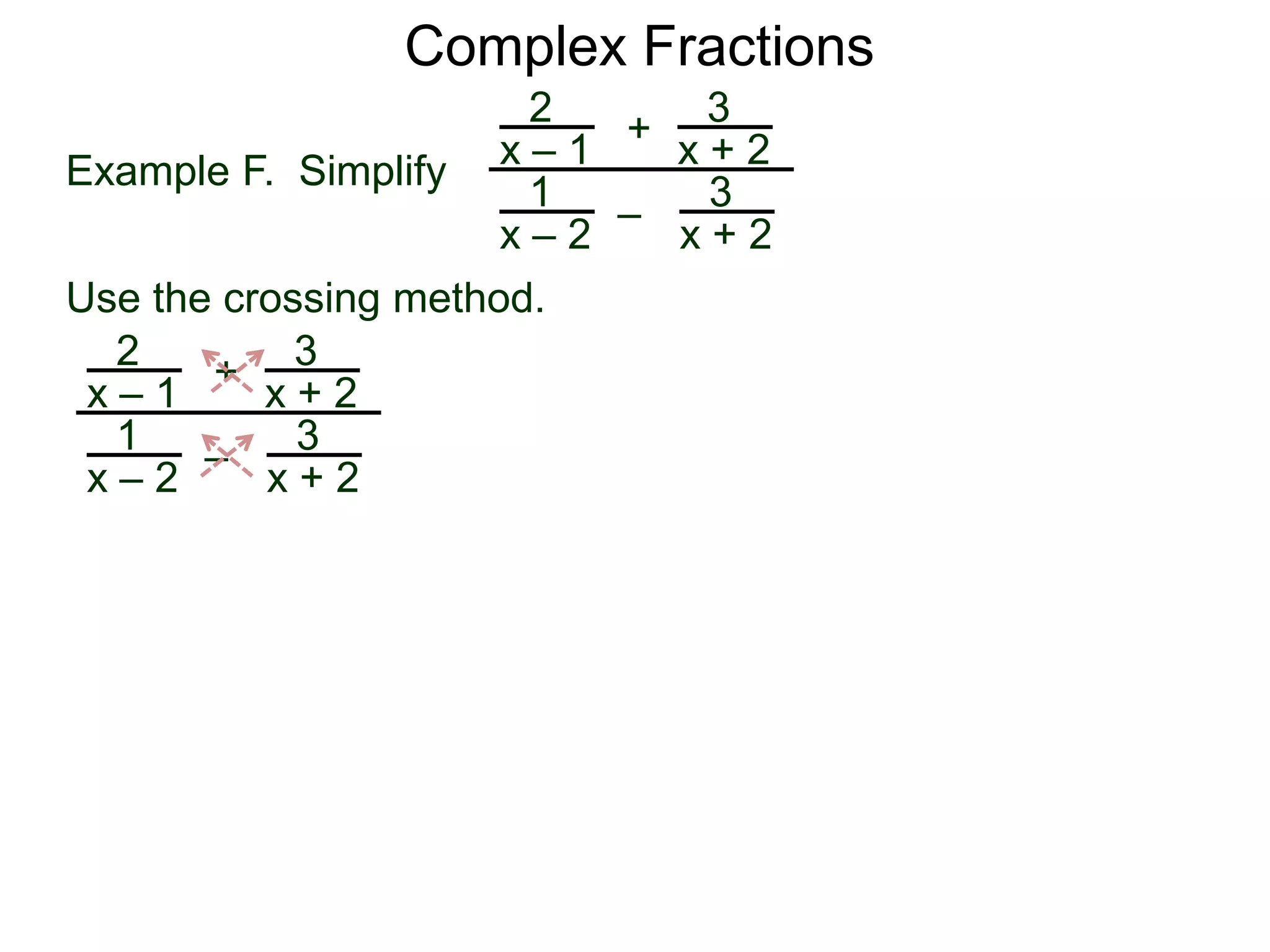
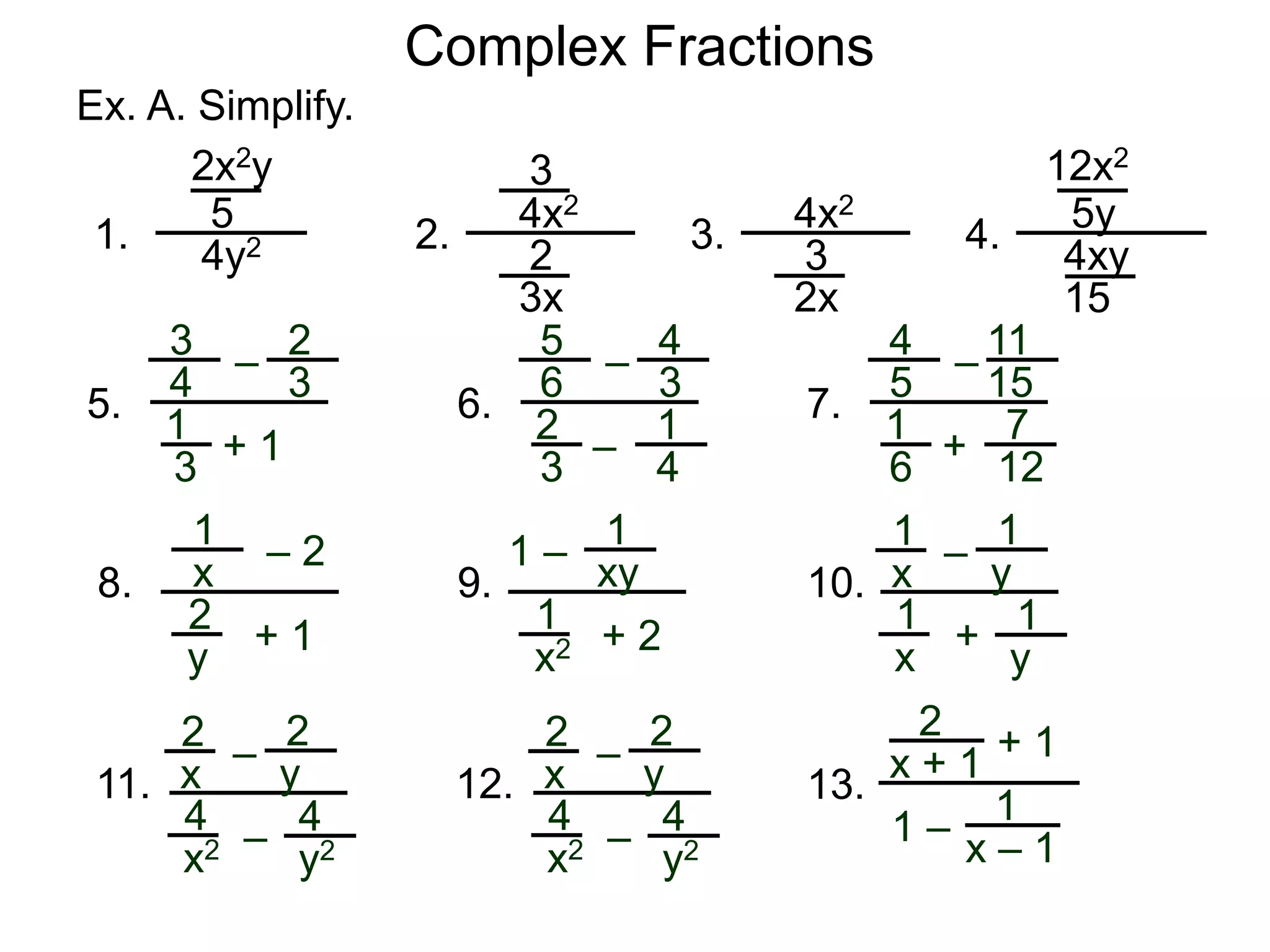
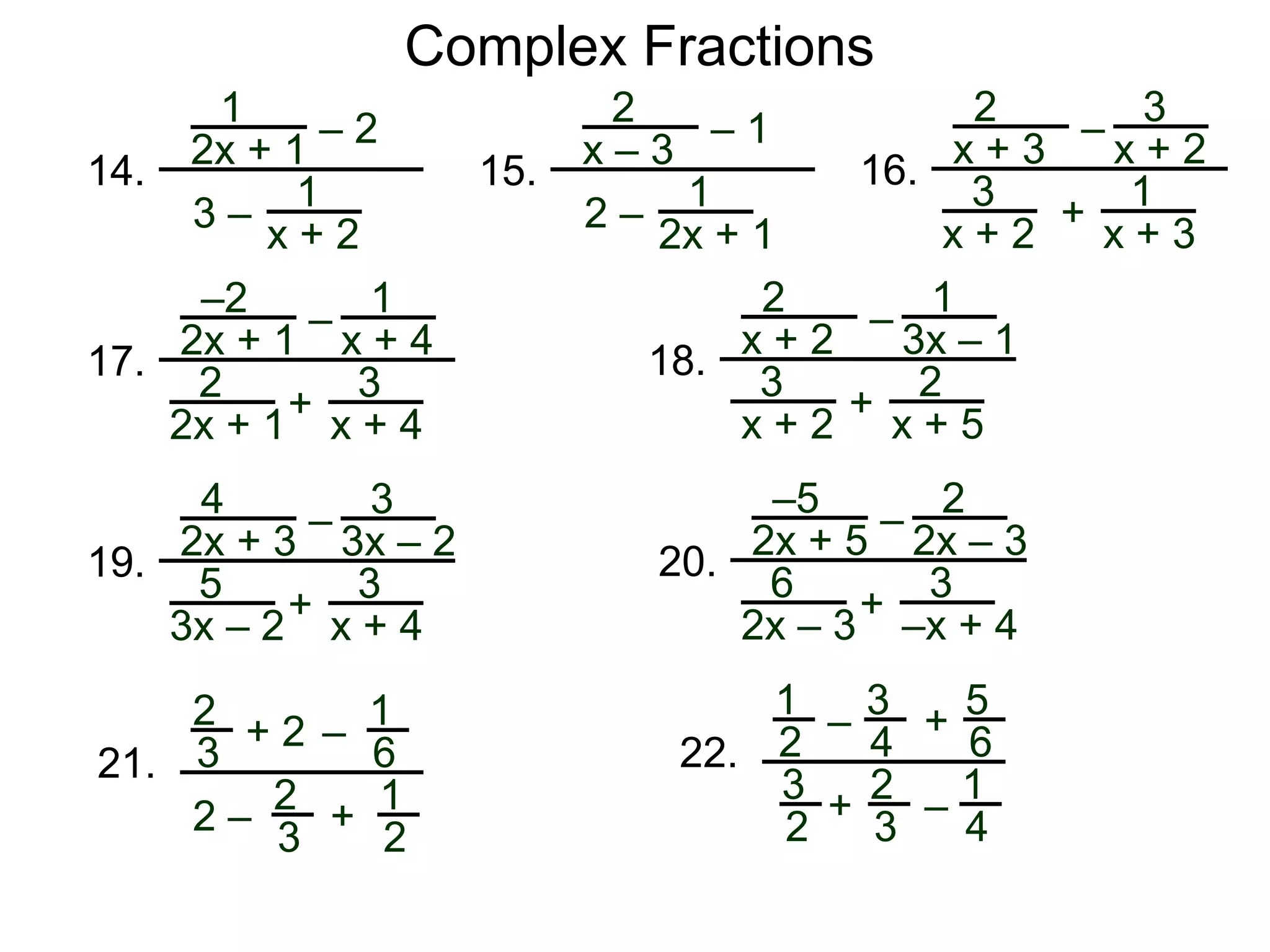
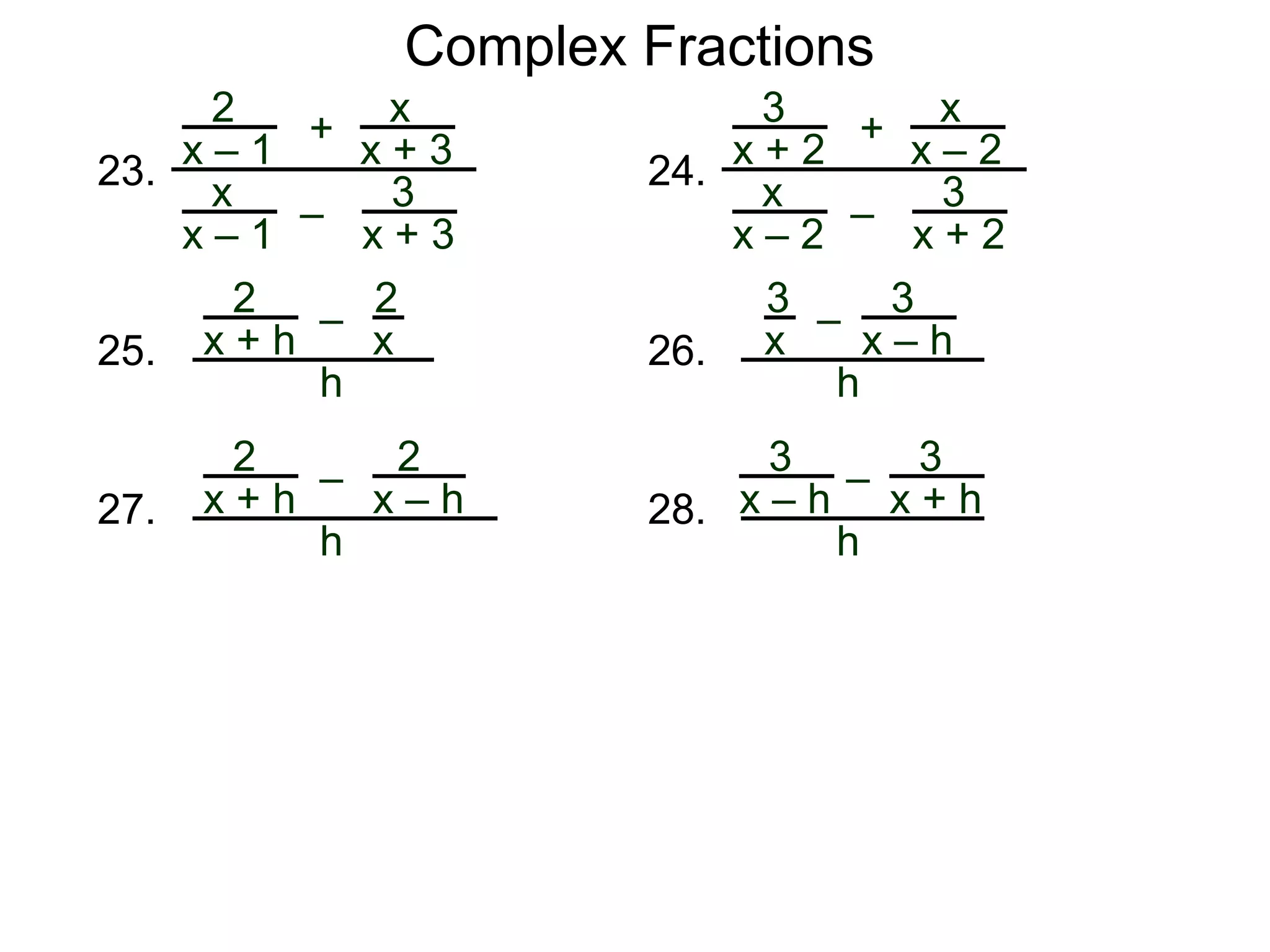
The document discusses two methods for simplifying complex fractions. A complex fraction is a fraction with fractions in the numerator or denominator. The first method reduces the complex fraction to an "easy" regular division problem by combining fractions in the numerator and denominator. The second method multiplies the lowest common denominator of all terms to the numerator and denominator to simplify. An example using each method is provided.

1. Complex Fractions
Frank Ma © 2011

2. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.

3. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.

4. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.

5. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction.

6. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication,

7. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D

8. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip

9. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6

10. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6
=
flip
4x2y
9 xy2
6

11. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6
=
flip
4x2y
9 xy2
6
3
2

12. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6
=
flip
4x2y
9 xy2
6
3
2x

13. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6
=
flip
4x2y
9 xy2
6
3
2x
y

14. Complex Fractions
A fraction with its numerator or the denominator containing
fraction(s) is called a complex fraction.
In other words, a complex fraction is a fractional expression
divided by another fractional expression.
We want to simplify complex fractions to regular fractions.
The “easy” complex fractions are just regular divisions of
of a fraction by another fraction. In this case just flip the
denominator then simplify the multiplication, i.e.
A
B
C
D
A
B C
D*
flip
Example A. Simplify
4x2y
9
xy2
6
=
flip
4x2y
9 xy2
6
=
3
2x
y
8x
3y

15. Complex Fractions
We give two methods for simplifying general complex
fractions.

16. Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem.

17. Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.

18. Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.

19. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1

20. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1x
x + 1
+ 1
1 –
x
x – 1

21. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1x
x + 1
+ 1
1 –
x
x – 1
=
x
x + 1 +
–
x
x – 1
1
1
1
1

22. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1x
x + 1
+ 1
1 –
x
x – 1
=
x
x + 1 +
–
x
x – 1
1
1
1
1
=
x + (x + 1)
x + 1

23. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1x
x + 1
+ 1
1 –
x
x – 1
=
x
x + 1 +
–
x
x – 1
1
1
1
1
=
x + (x + 1)
x + 1
(x – 1) – x
x – 1

24. Example B. Simplify
Complex Fractions
We give two methods for simplifying general complex
fractions. The first method is to reduce the problem to an
“easy” problem. We do this by combining the numerator
into one fraction and the denominator into one fraction.
We can use cross multiplication for combining two fractions.
x
x + 1
+ 1
1 – x
x – 1x
x + 1
+ 1
1 –
x
x – 1
=
x
x + 1 +
–
x
x – 1
1
1
1
1
=
x + (x + 1)
x + 1
(x – 1) – x
x – 1
=
2x + 1
x + 1
–1
x – 1

25. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
2x + 1
x + 1
–1
x – 1
Therefore,

26. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
2x + 1
x + 1
–1
x – 1
Therefore,
=
(2x + 1)
(x + 1)
(x – 1)
(–1)

27. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
2x + 1
x + 1
–1
x – 1
Therefore,
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

28. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

29. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

30. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

31. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1) (–1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)

32. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1) (–1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)

33. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
This is OK since is 1.
12
121
(–1)

34. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
6
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
Distribute the multiplication.
(–1)

35. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
6 12
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
Distribute the multiplication.
(–1)

36. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
6 12 2
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
Distribute the multiplication.
(–1)

37. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
6 12 2
12 4 3
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
Distribute the multiplication.
(–1)

38. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
=
6 12 2
12 4 3
18 + 12 – 10
12 – 8 + 9
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

39. Complex Fractions
x
x + 1
+ 1
1 – x
x – 1
=
Therefore,
The second method is to multiply the LCD of all the terms to
the numerator and the denominator of the complex fraction.
Example C. Simplify
3
2
+ 1
1 –
– 5
6
2
3
3
4
+
The LCD of
2
3
3
2
5
6
3
4, , , is 12.
Multiply 12 to the top and bottom of the complex fraction.
3
2
+ 1
1 –
–
5
6
2
3
3
4
+(
( )
)
12
12
=
6 12 2
12 4 3
18 + 12 – 10
12 – 8 + 9 =
20
13
2x + 1
x + 1
–1
x – 1
=
(2x + 1)
(x + 1)
(x – 1)
= –
(2x + 1)
(x + 1)
(x – 1)
(–1)

40. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
x
y
y2

41. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
y2
x2 x
yy2 ,

42. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2

43. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2

44. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
1

45. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
y21

46. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
y2
y2y
1

47. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
=
y2
y2y
1
x2 – y2
xy + y2

48. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
=
y2
y2y
1
x2 – y2
xy + y2
= (x – y)(x + y)
y(x + y)
To simplify this, put it in the factored form .

49. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
=
y2
y2y
1
x2 – y2
xy + y2 To simplify this, put it in the factored form .
= (x – y)(x + y)
y(x + y)

50. Complex Fractions
x2
+ 1
– 1
Example D. Simplify
The LCD of
x
y
is y2.
Multiply the LCD to top and bottom of the complex fraction.
y2
x2 x
yy2 ,
x2
+ 1
– 1
x
y
y2
(
(
)
) y2
y2
=
y2
y2y
1
x2 – y2
xy + y2 To simplify this, put it in the factored form .
= (x – y)(x + y)
y(x + y)
= x – y
y

51. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
3
x + 2
x
x – 2

52. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).

53. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2

54. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)

55. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
(x + 2)

56. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
(x + 2) (x – 2)

57. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
=
(x + 2)
(x + 2)
(x – 2)
(x – 2)
x(x + 2) + 3(x – 2)
x(x + 2) – 3(x – 2) Expand and put the fraction
in the factored form.

58. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
=
(x + 2)
(x + 2)
(x – 2)
(x – 2)
x(x + 2) + 3(x – 2)
x(x + 2) – 3(x – 2) Expand and put the fraction
in the factored form.
=
x2 + 2x + 3x – 6
x2 + 2x – 3x + 6

59. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
=
(x + 2)
(x + 2)
(x – 2)
(x – 2)
x(x + 2) + 3(x – 2)
x(x + 2) – 3(x – 2) Expand and put the fraction
in the factored form.
=
x2 + 2x + 3x – 6
x2 + 2x – 3x + 6
=
x2 + 5x – 6
x2 – x + 6

60. Complex Fractions
x
x – 2
–
+
3
x + 2
Example E. Simplify
The LCD of
3
x + 2
x
x – 2
x
x – 2
x
x – 2
3
x + 2
3
x + 2, , , is (x – 2)(x + 2).
Multiply the LCD to top and bottom of the complex fraction.
x
x – 2
–
+
3
x + 2
3
x + 2
x
x – 2
(
( )
)
(x – 2)(x + 2)
(x – 2)(x + 2)
=
(x + 2)
(x + 2)
(x – 2)
(x – 2)
x(x + 2) + 3(x – 2)
x(x + 2) – 3(x – 2) Expand and put the fraction
in the factored form.
=
x2 + 2x + 3x – 6
x2 + 2x – 3x + 6
=
x2 + 5x – 6
x2 – x + 6
This is the simplified.=
(x + 6)(x – 1)
x2 – x + 6

61. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2

62. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.

63. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2

64. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2
=
2(x + 2) + 3(x – 1)
(x – 1)(x + 2)
2(x + 3) – 3(x – 2)
(x – 2)(x + 2)

65. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2
=
2(x + 2) + 3(x – 1)
(x – 1)(x + 2)
2(x + 3) – 3(x – 2)
(x – 2)(x + 2)
=
5x +1
(x – 1)(x + 2)
– x + 12
(x – 2)(x + 2)

66. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2
=
2(x + 2) + 3(x – 1)
(x – 1)(x + 2)
2(x + 3) – 3(x – 2)
(x – 2)(x + 2)
flip the bottom
fraction
=
5x +1
(x – 1)(x + 2)
– x + 12
(x – 2)(x + 2)

67. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2
=
2(x + 2) + 3(x – 1)
(x – 1)(x + 2)
2(x + 3) – 3(x – 2)
(x – 2)(x + 2)
flip the bottom
fraction
=
5x +1
(x – 1)(x + 2)
– x + 12
(x – 2)(x + 2)
=
(5x +1)
(x – 1)(x + 2) (– x + 12)
(x – 2)(x + 2)

68. Complex Fractions
2
x – 1
–
+
3
x + 2
Example F. Simplify
3
x + 2
1
x – 2
Use the crossing method.
2
x – 1
–
+
3
x + 2
3
x + 2
1
x – 2
=
2(x + 2) + 3(x – 1)
(x – 1)(x + 2)
2(x + 3) – 3(x – 2)
(x – 2)(x + 2)
flip the bottom
fraction
=
5x +1
(x – 1)(x + 2)
– x + 12
(x – 2)(x + 2)
=
(5x +1)
(x – 1)(x + 2) (– x + 12)
(x – 2)(x + 2)
=
(5x + 1)(x – 2)
(x – 1)(–x + 12)

69. Complex Fractions
Ex. A. Simplify.
1.
2x2y
5
4y2 2.
3
4x2
3x
2 3.
4x2
2x
3 4.
12x2
5y
4xy
15
3
+ 1
–
1
3
4
5.
2
3
5
–
–
2
3
6
6.
4
3
1
4
4
+
–
1
6
5
7.
11
15
7
12
1
+ 1
– 2
2
y
x8.
1
+ 2
1 –
1
x2
xy9.
1
+
–
1
x
y10.
1
x
1
y
2
–
–
4
x2
y11.
2
x
4
y2
2
–
–
4
x2
y12.
2
x
4
y2
2
x + 1 + 1
1 –
1
x – 1
13.

70. Complex Fractions
1
2x + 1
– 2
3 –
1
x + 2
14.
2
x – 3
– 1
2 –
1
2x + 1
15.
2
x + 3
–
+
1
x + 3
16.
3
x + 2
3
x + 2
–2
2x + 1
–
+
3
x + 4
17.
1
x + 4
2
2x + 1
2
x + 2
–
+ 2
x + 5
18.
1
3x – 1
3
x + 2
4
2x + 3
–
+
3
x + 4
19.
3
3x – 2
5
3x – 2
–5
2x + 5
–
+ 3
–x + 4
20.
2
2x – 3
6
2x – 3
2
3
+ 2
2 –
–
1
6
2
3
1
2
+
21.
1
2
– +
5
6
2
3
1
4
–
22.
3
4
3
2
+

71. Complex Fractions
23.
2
x – 1
–
+
3
x + 3
x
x + 3
x
x – 1
24.
3
x + 2
–
+
3
x + 2
x
x – 2
x
x – 2
25.
2
x + h
–
2
x
h
26.
3
x – h
–
3
x
h
27.
2
x + h
– 2
x – h
h
28.
3
x + h
–
h
3
x – h