Uploaded byelem-alg-sample
PPTX, PDF871 views

3 rectangular coordinate system

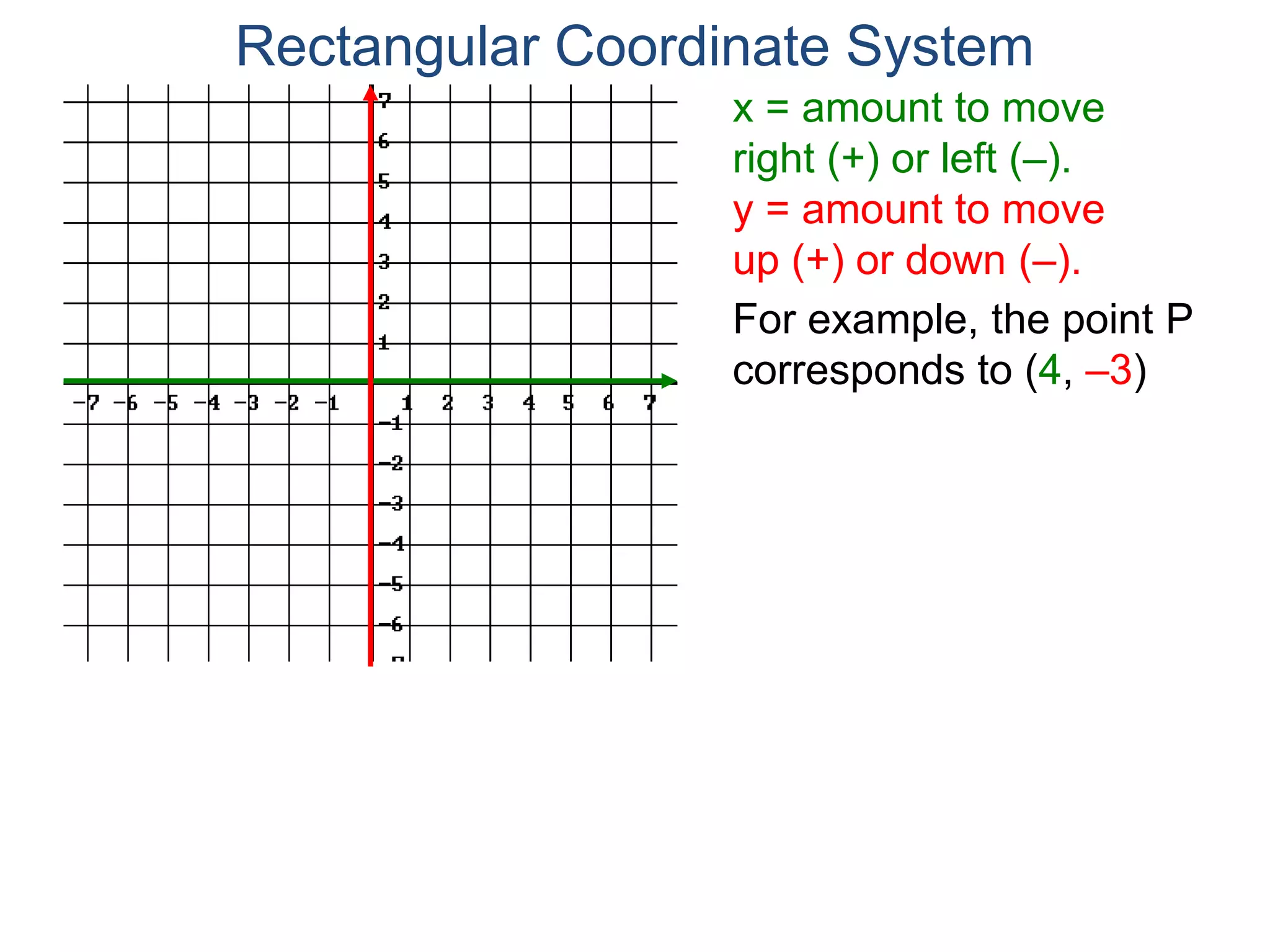
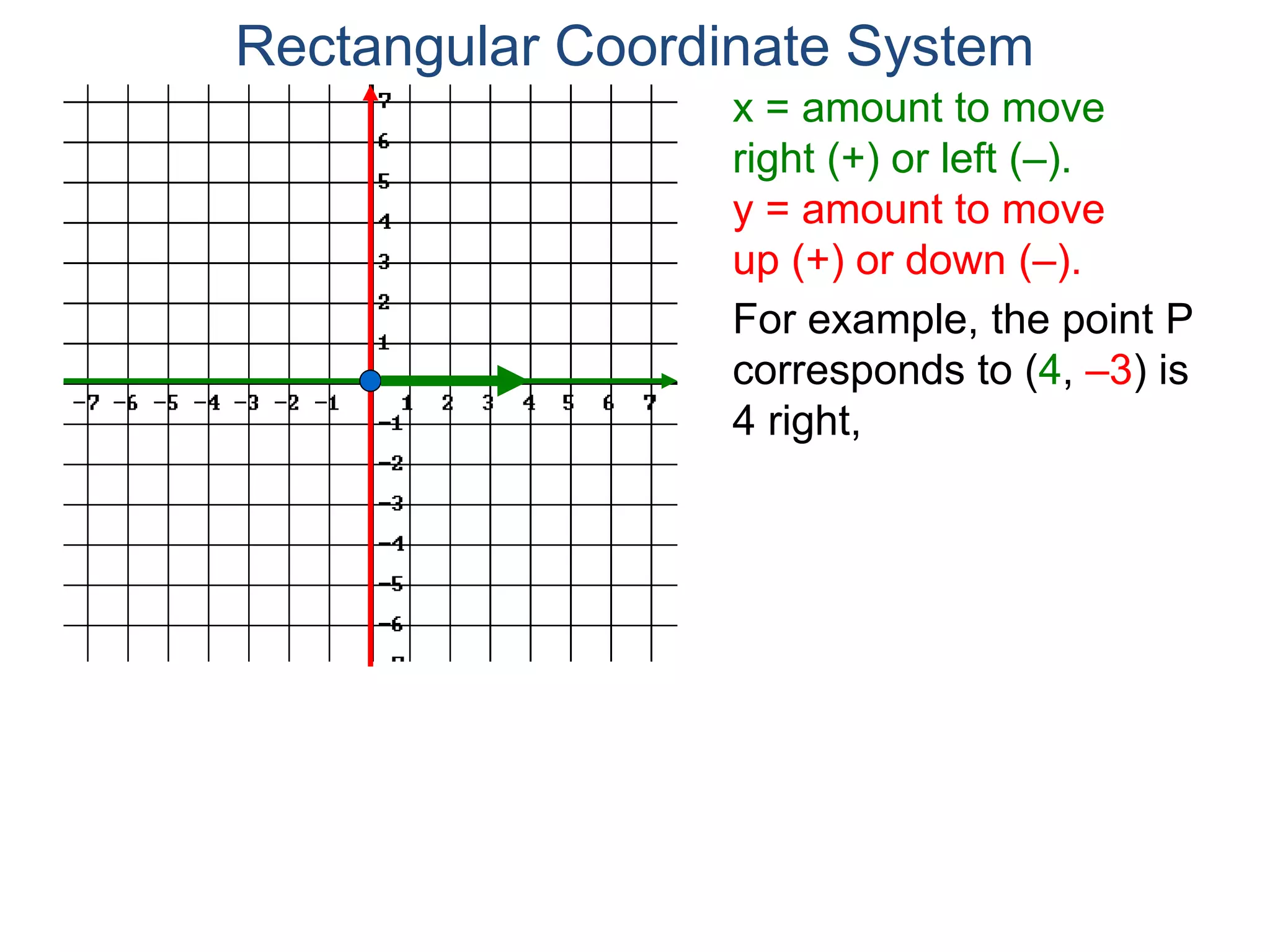
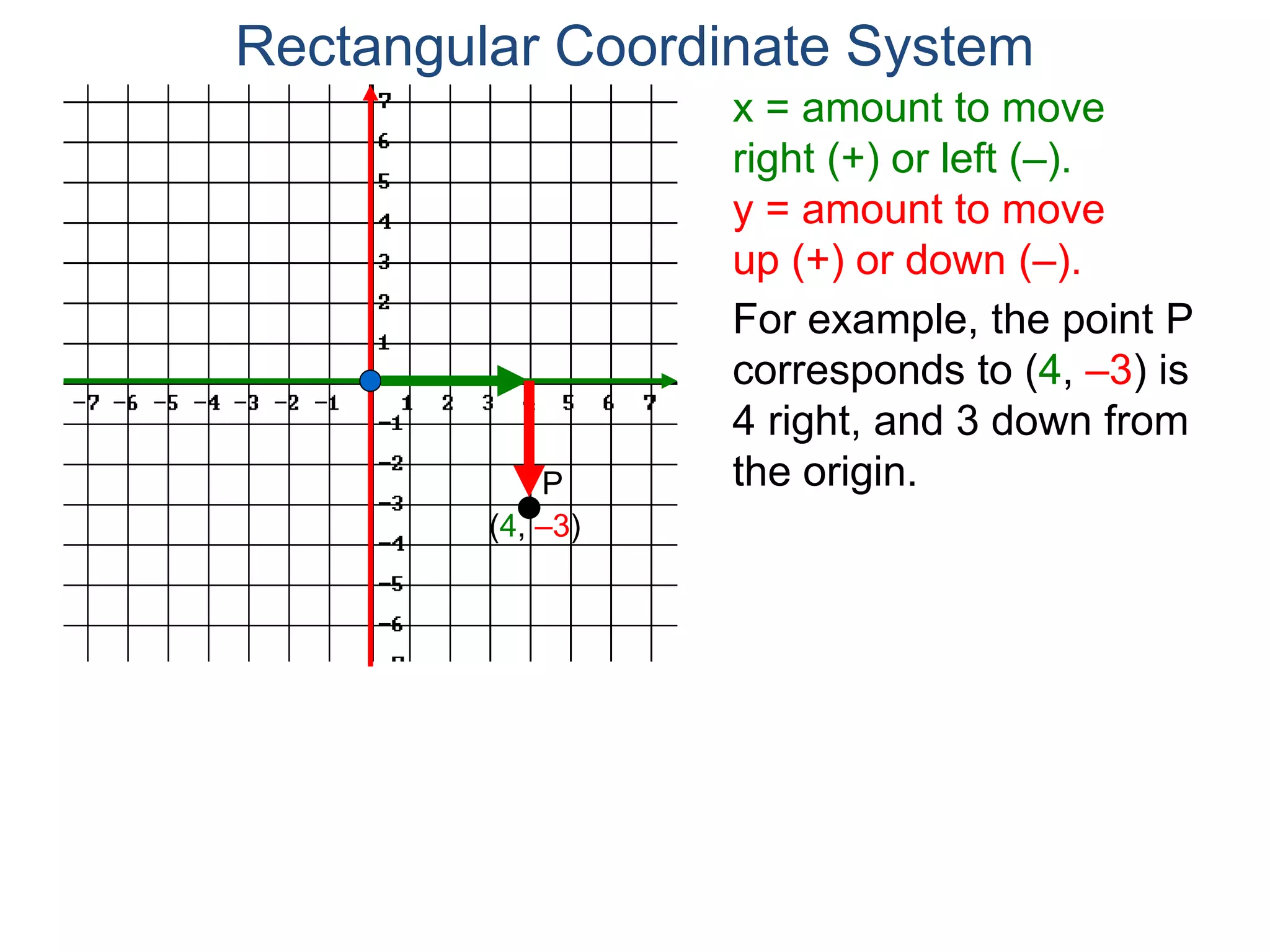
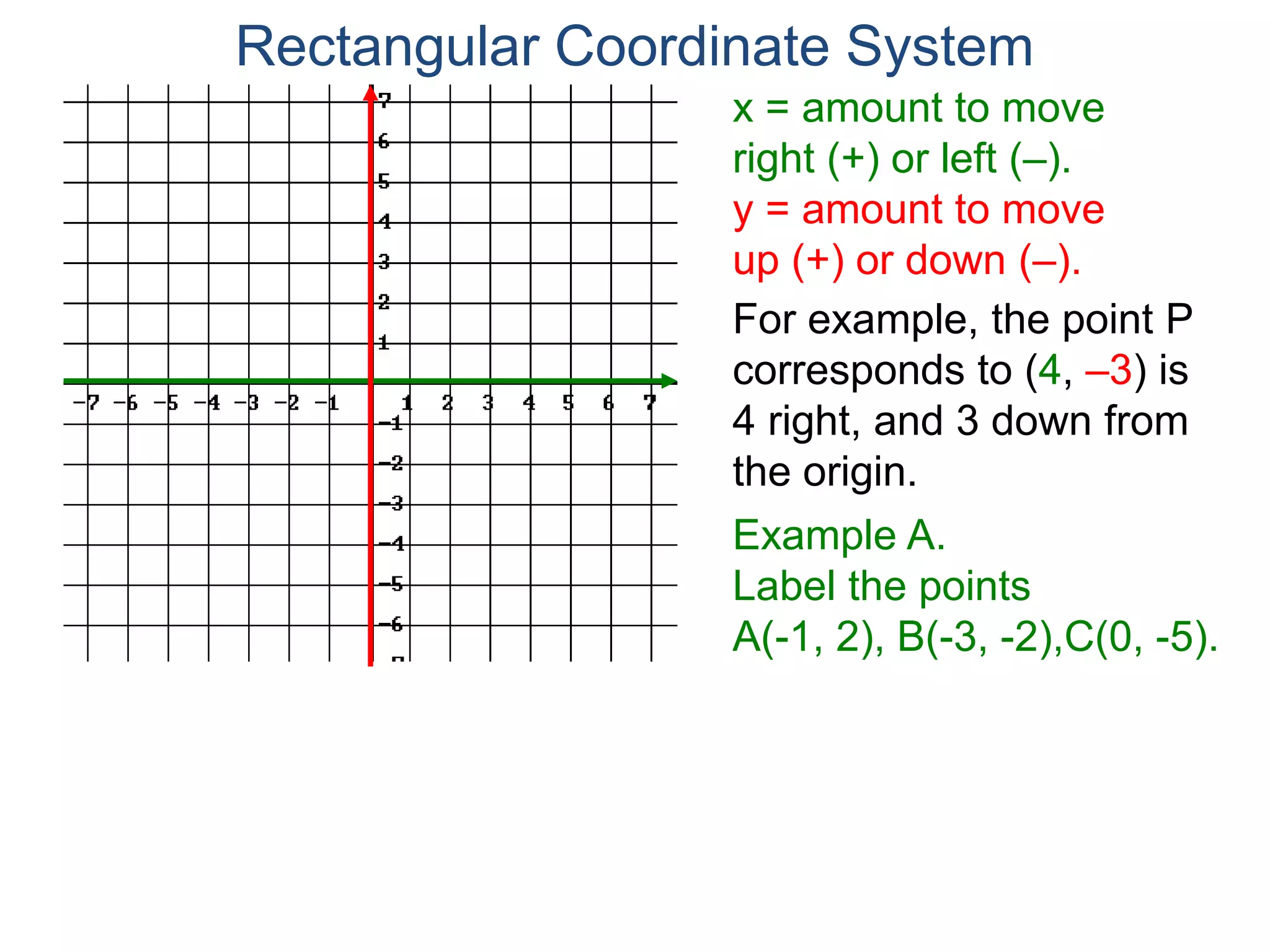
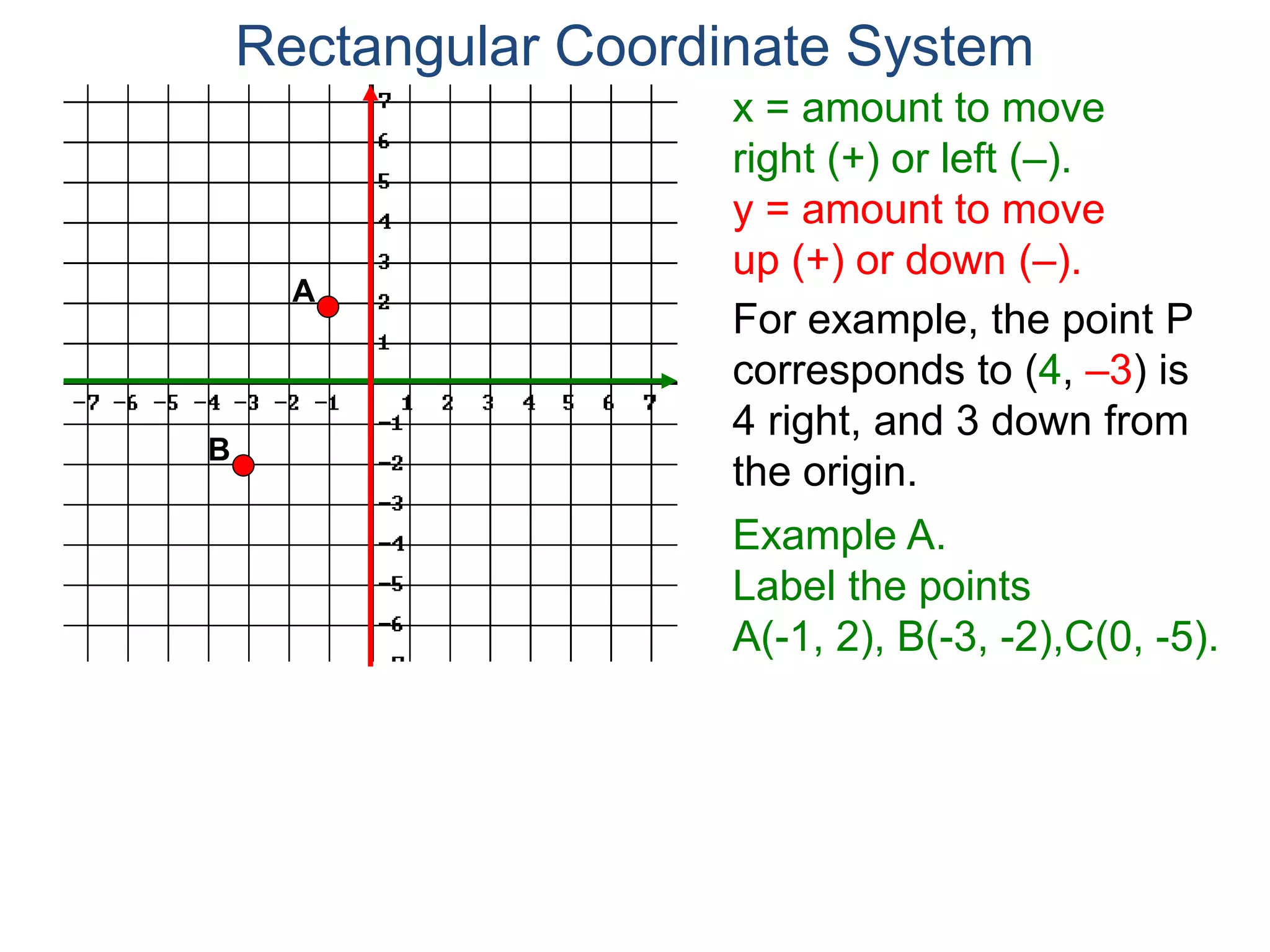
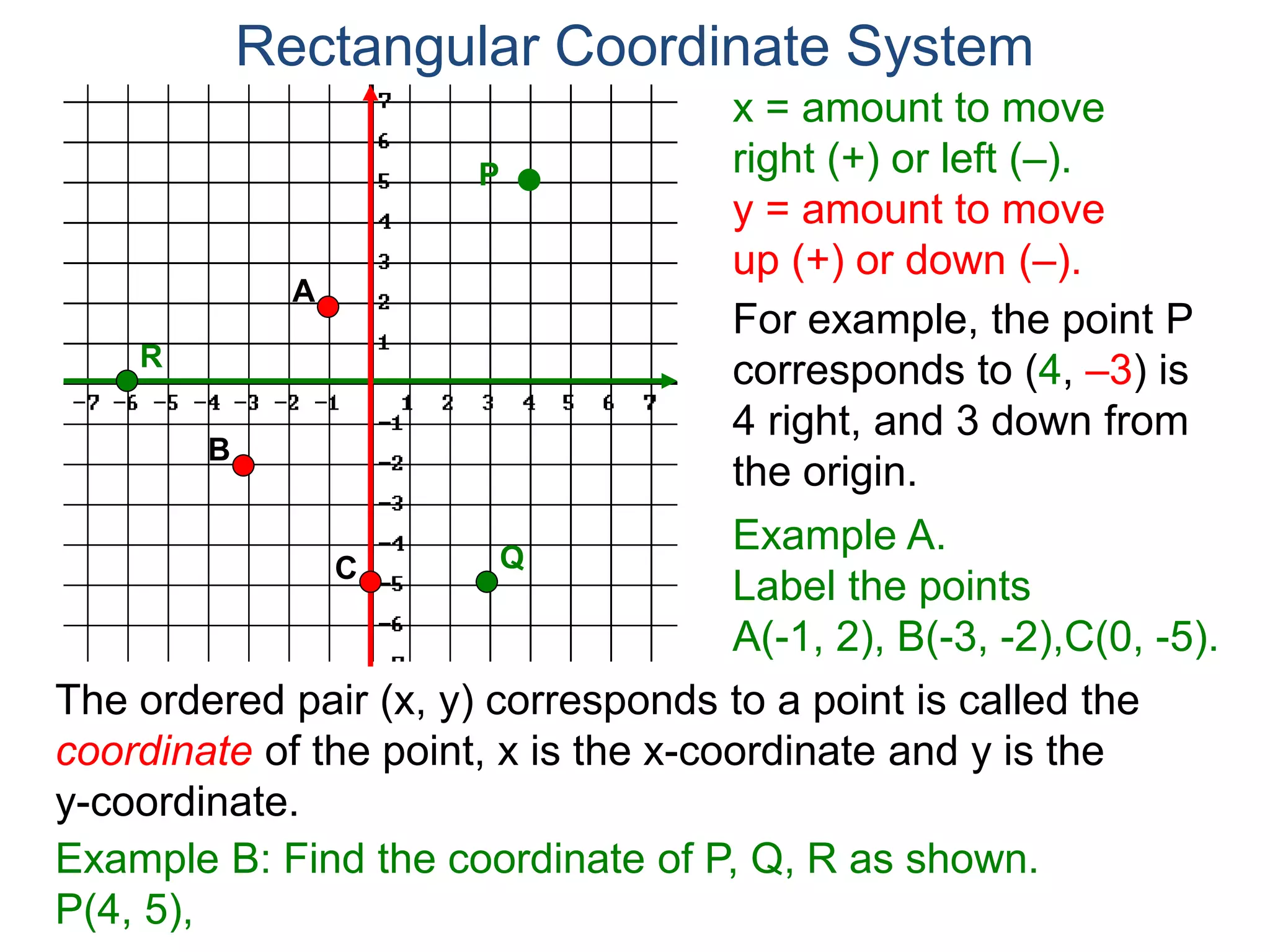
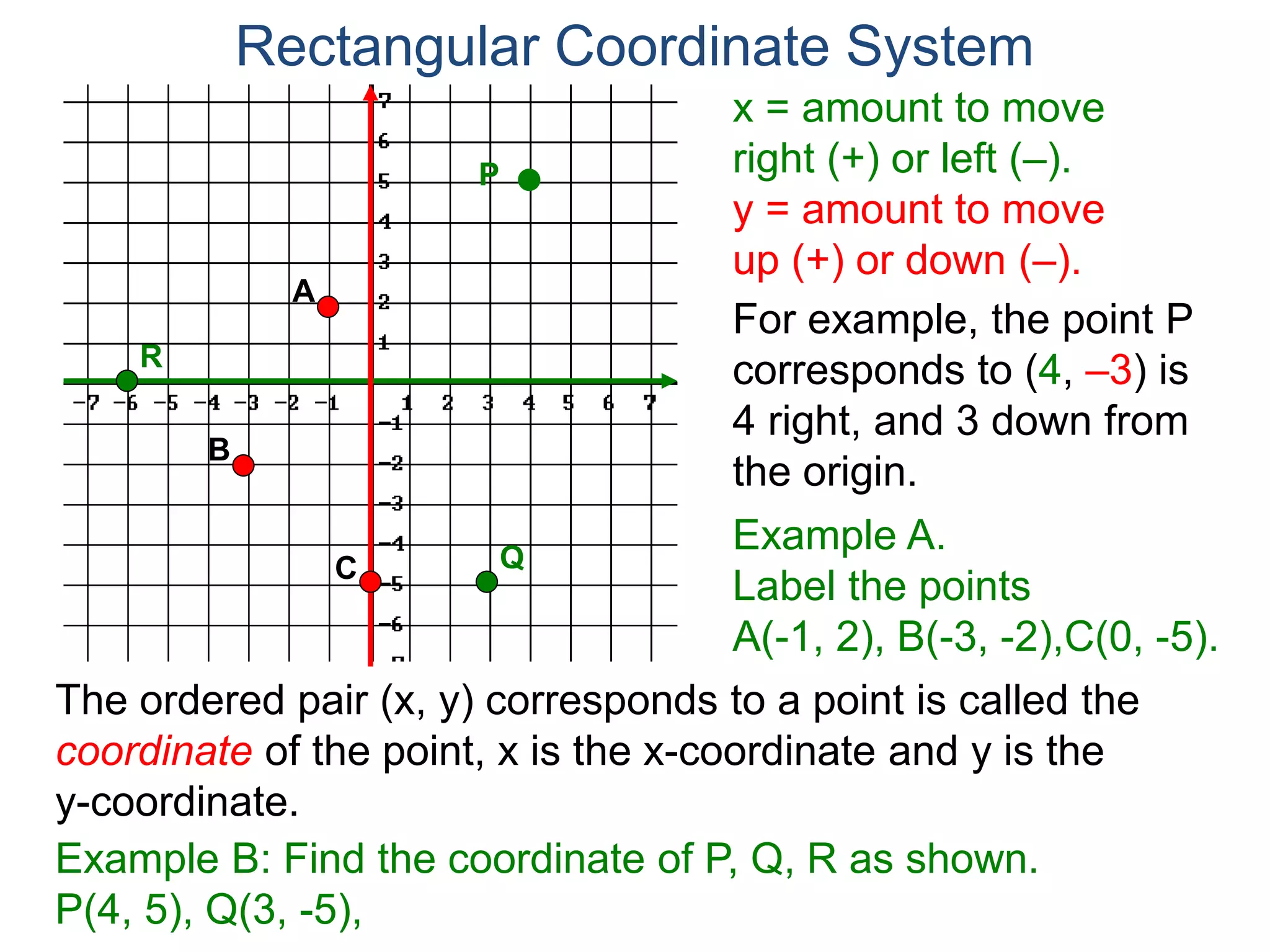
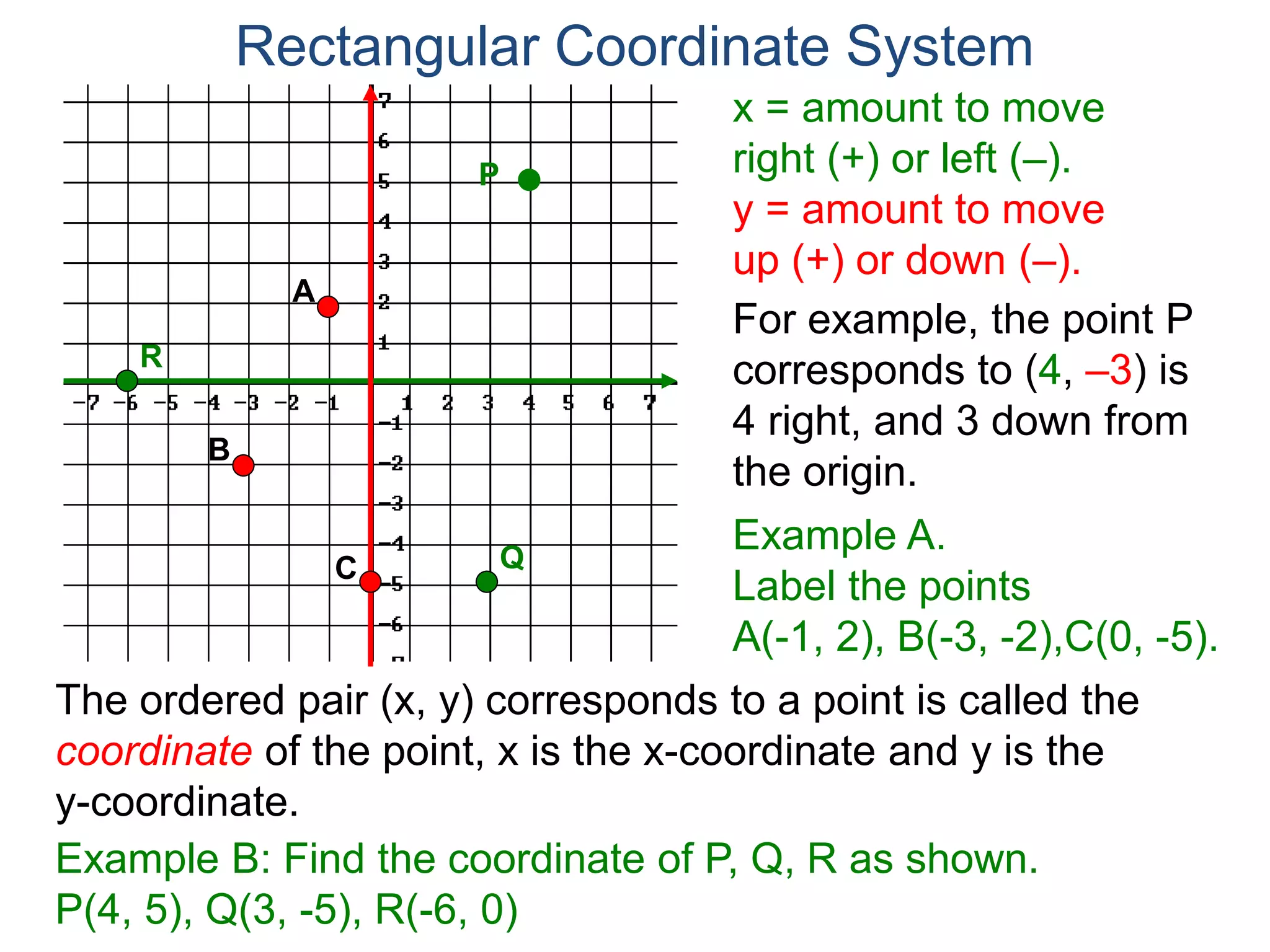
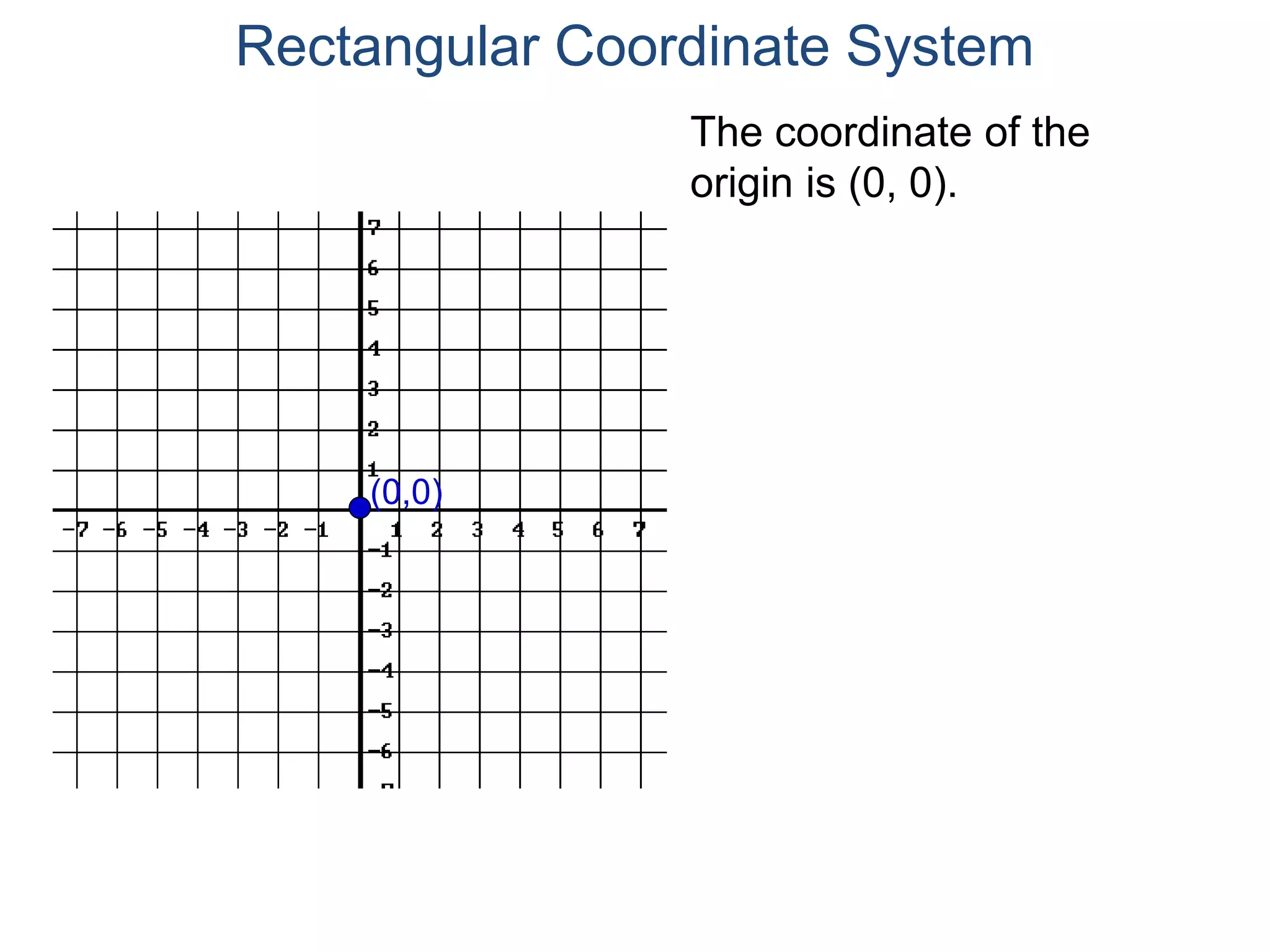
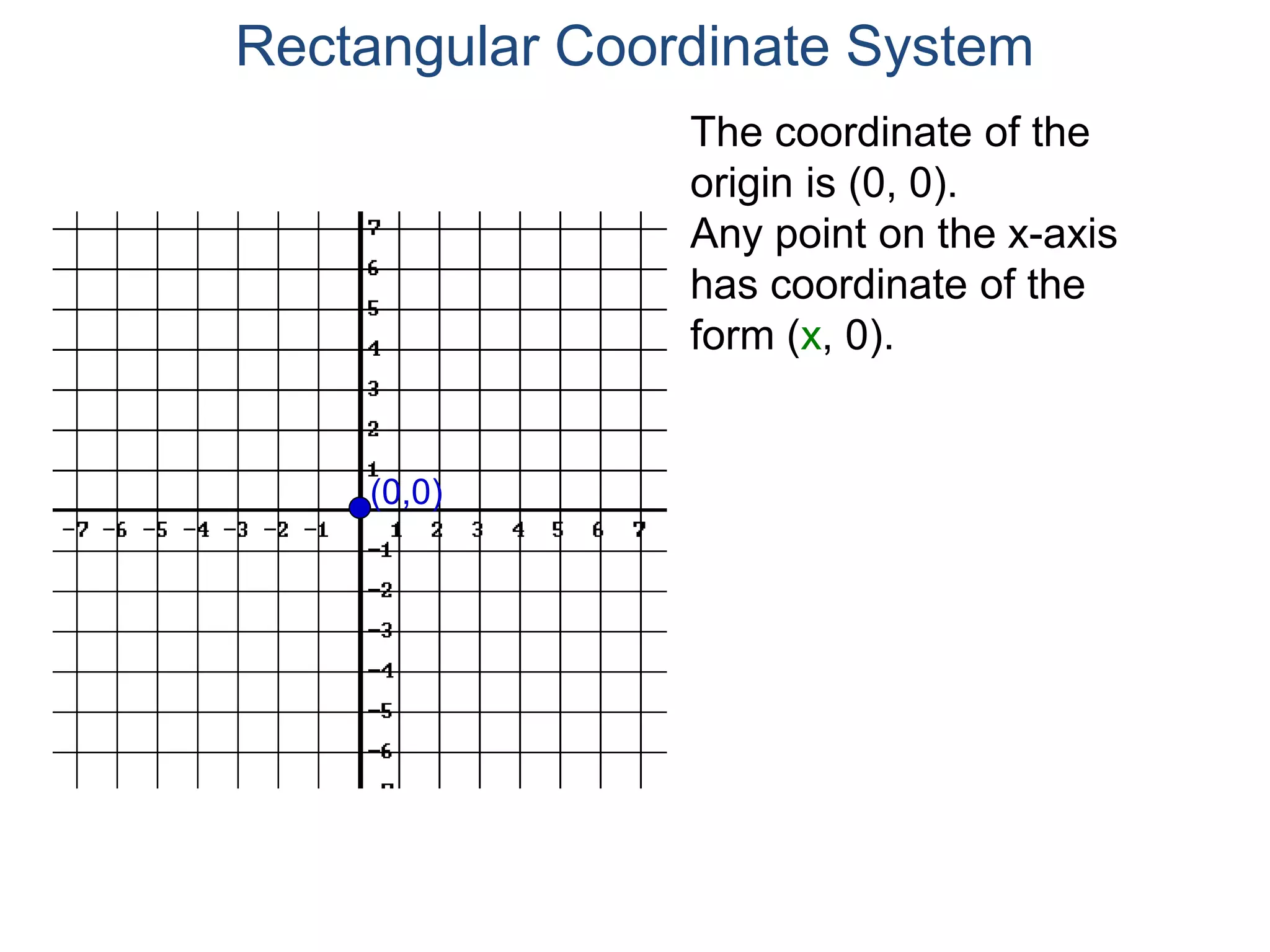
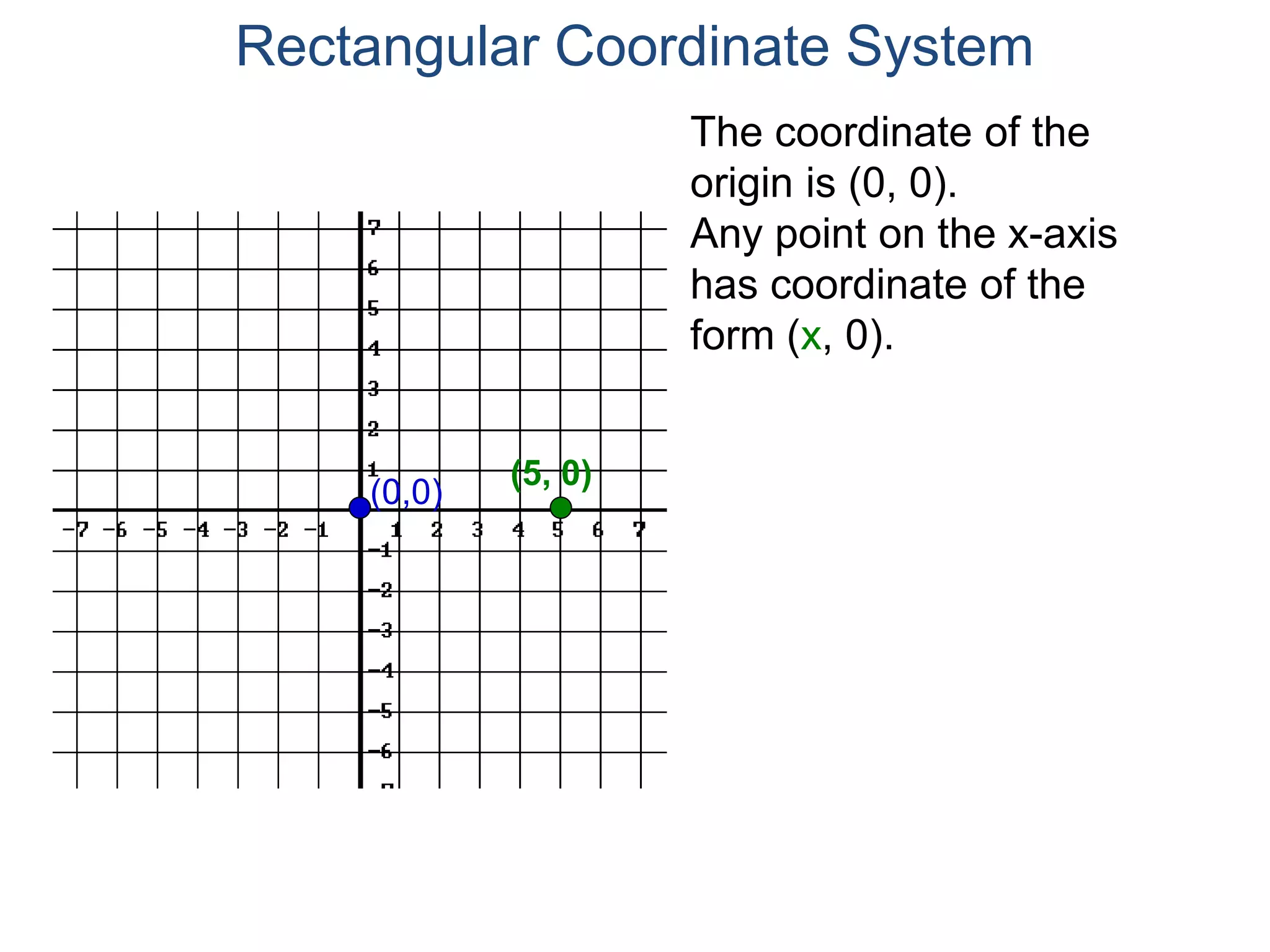
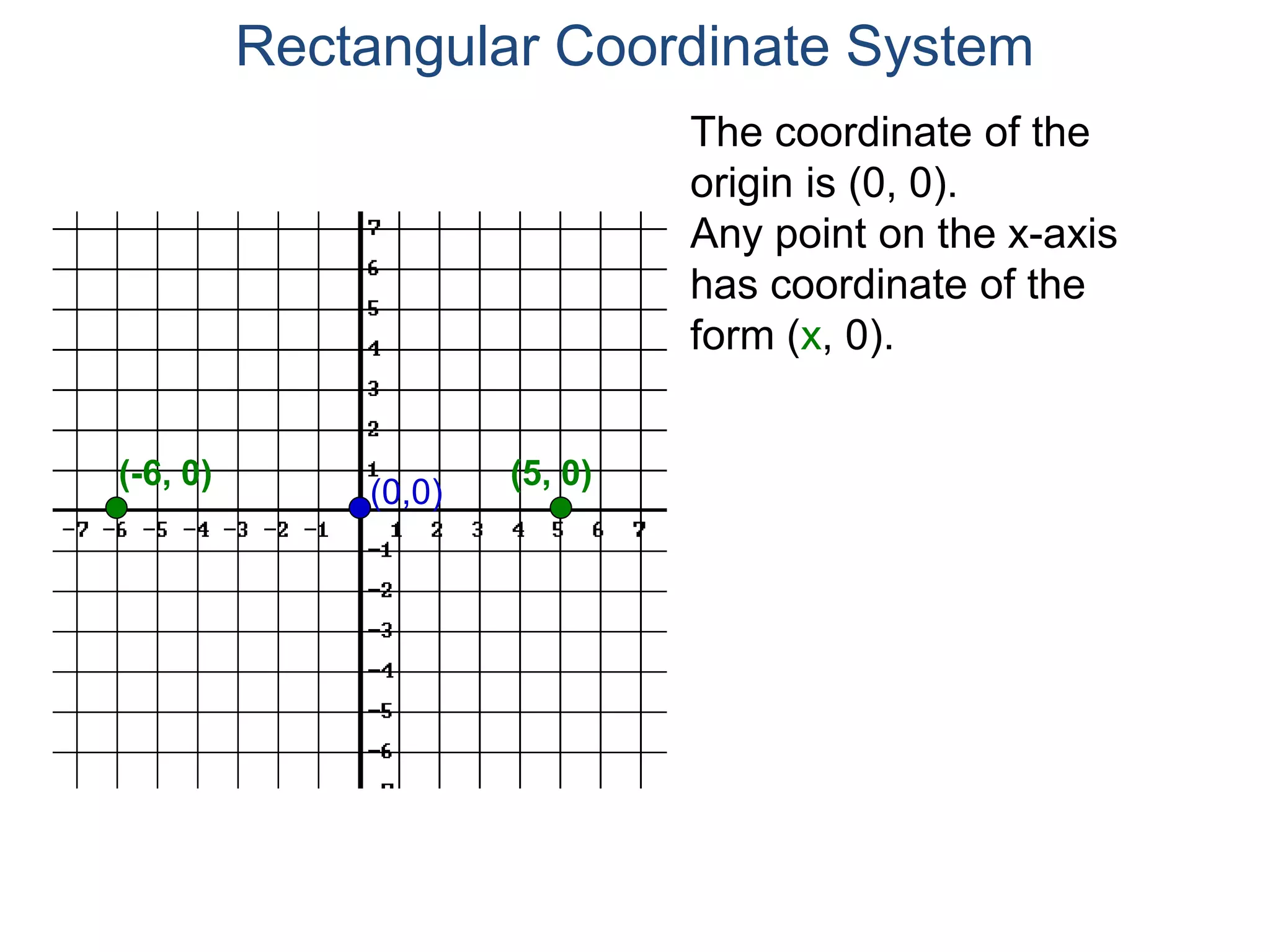
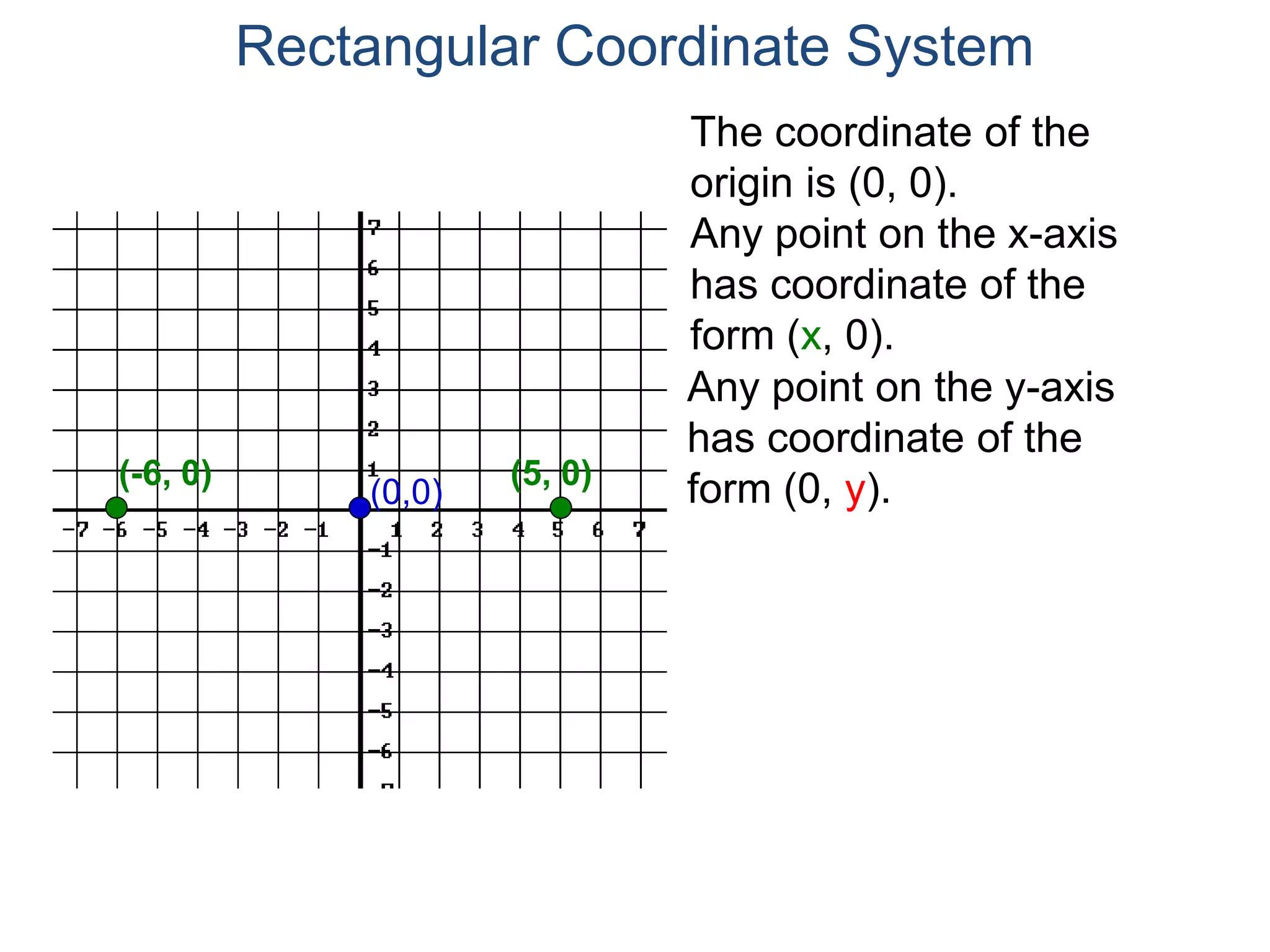
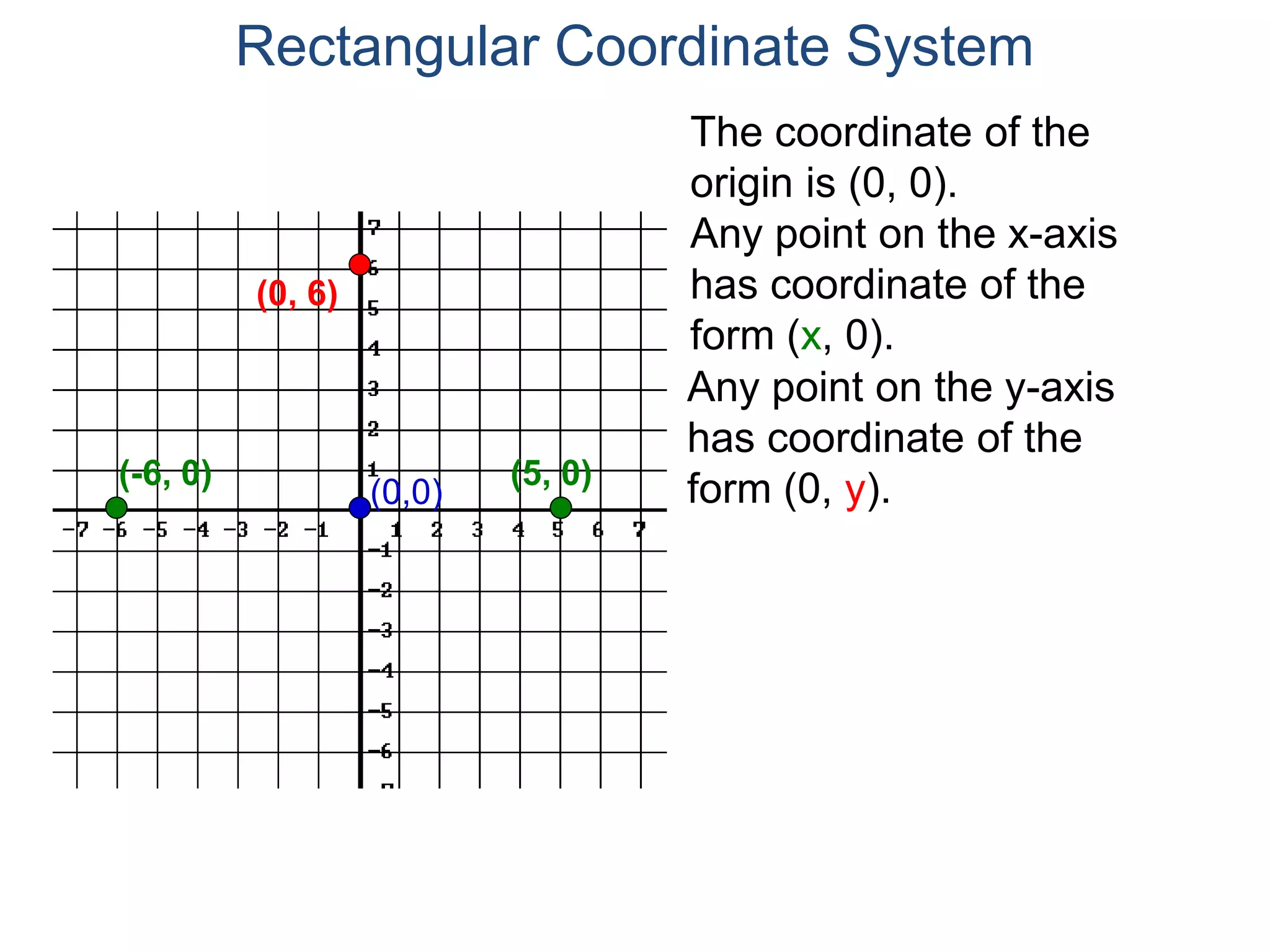
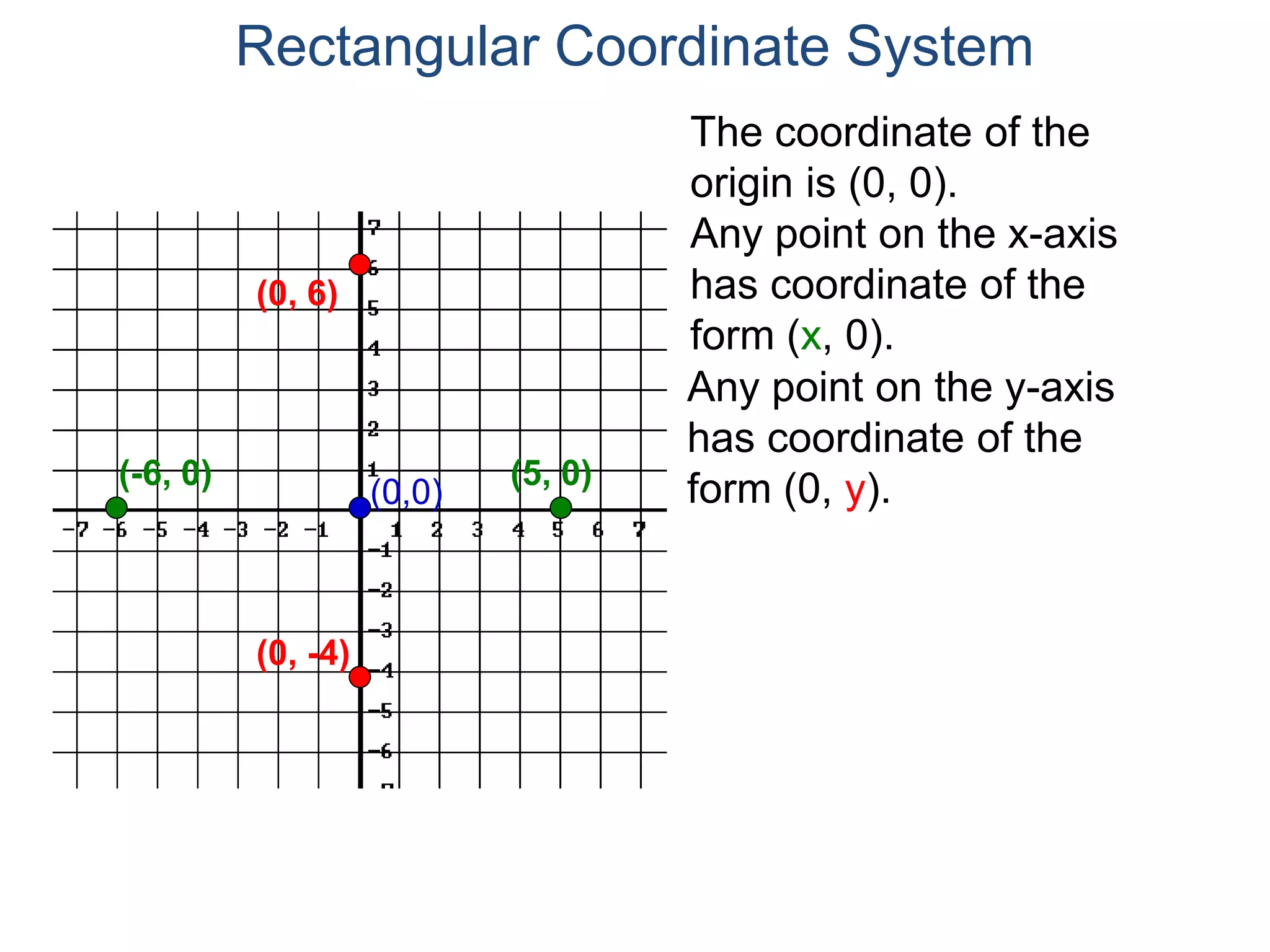
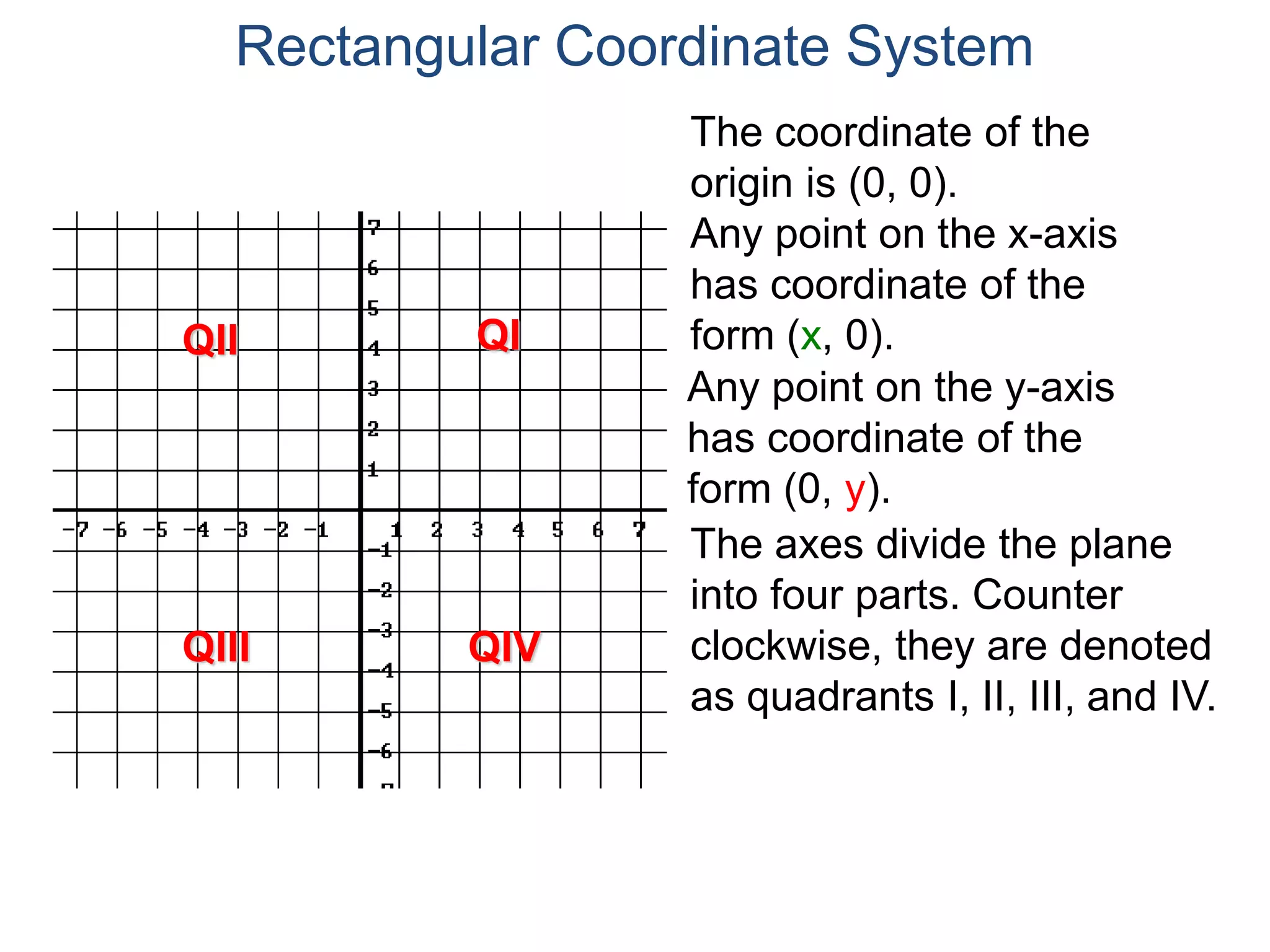
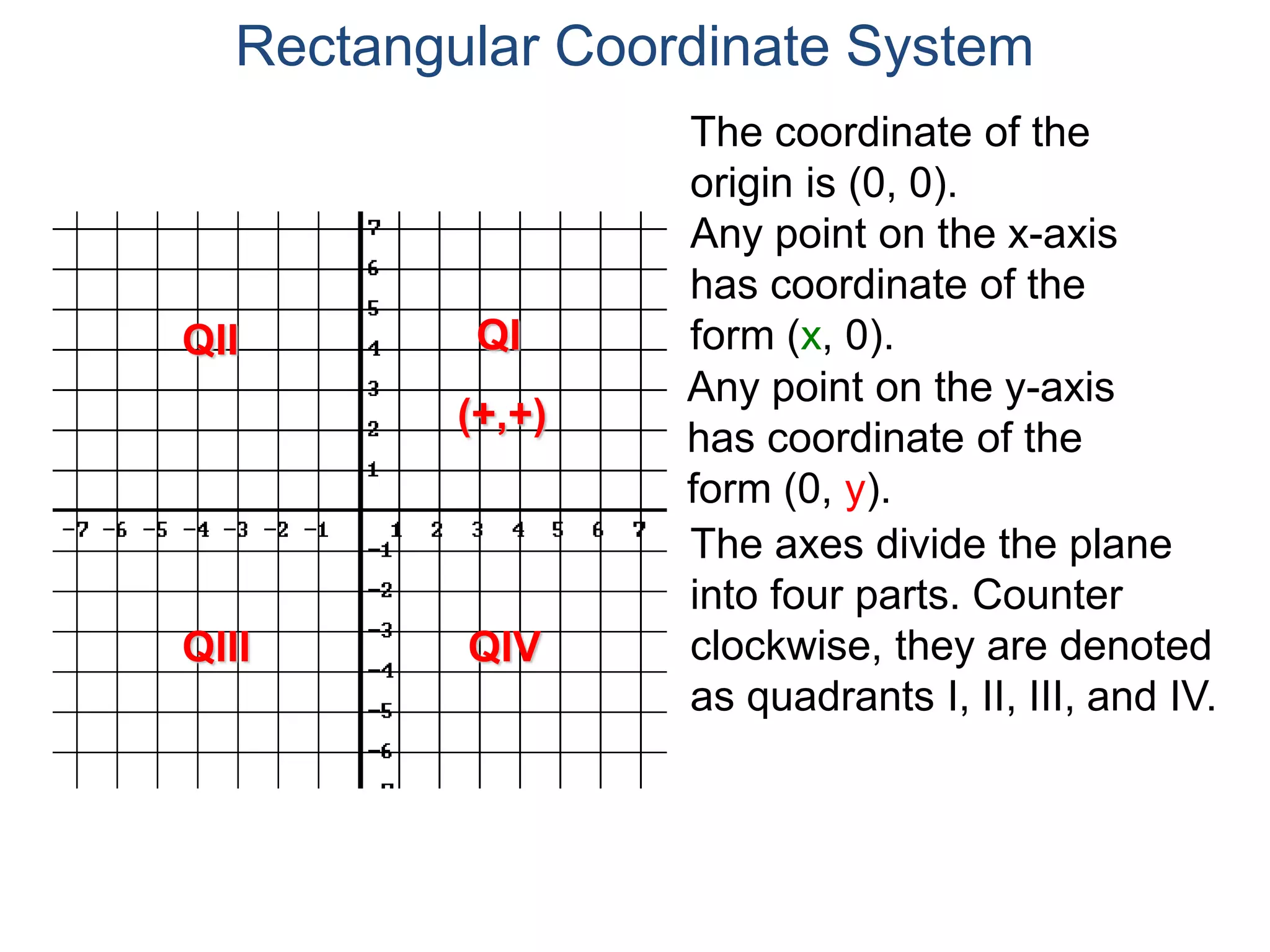
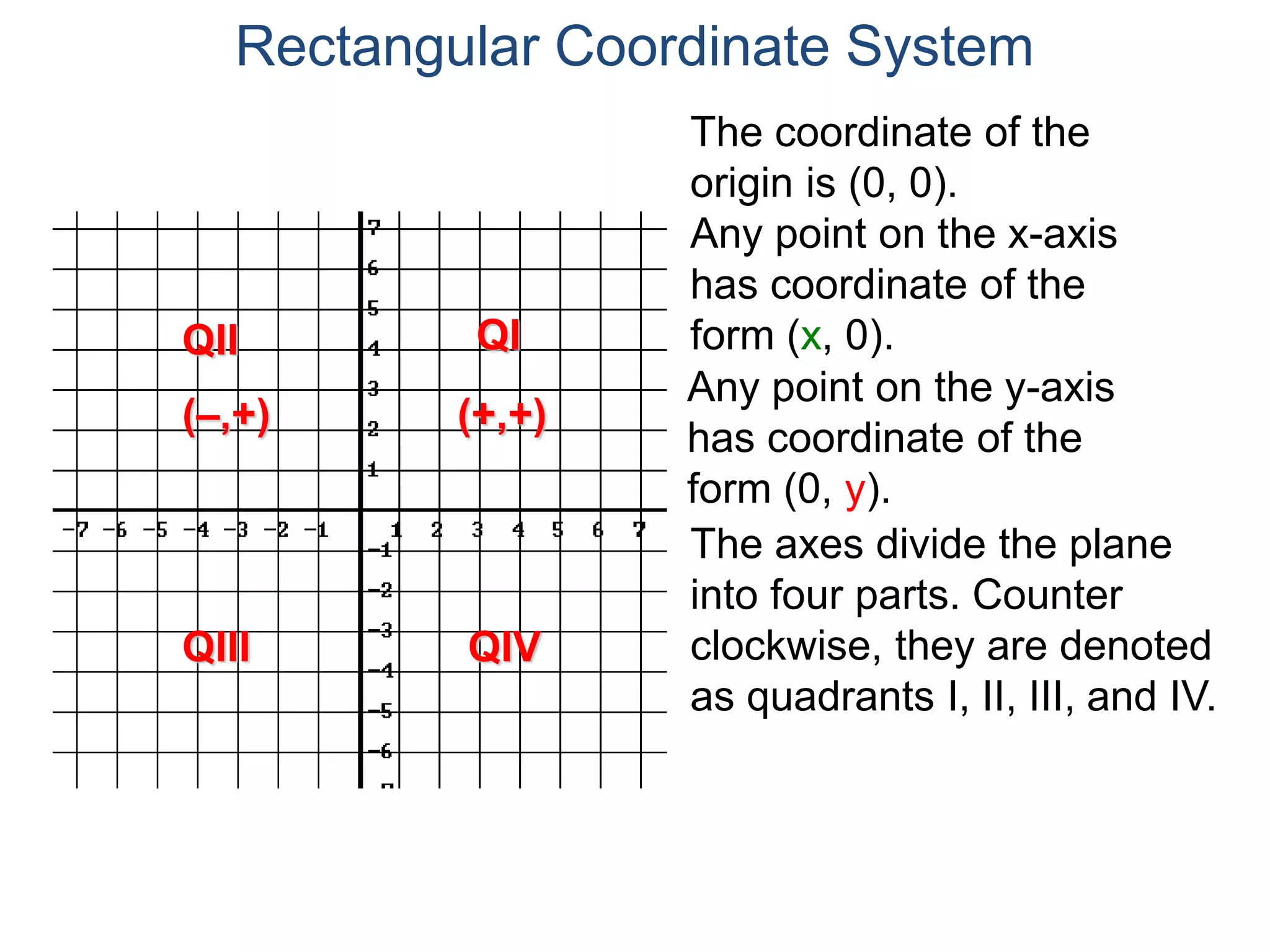
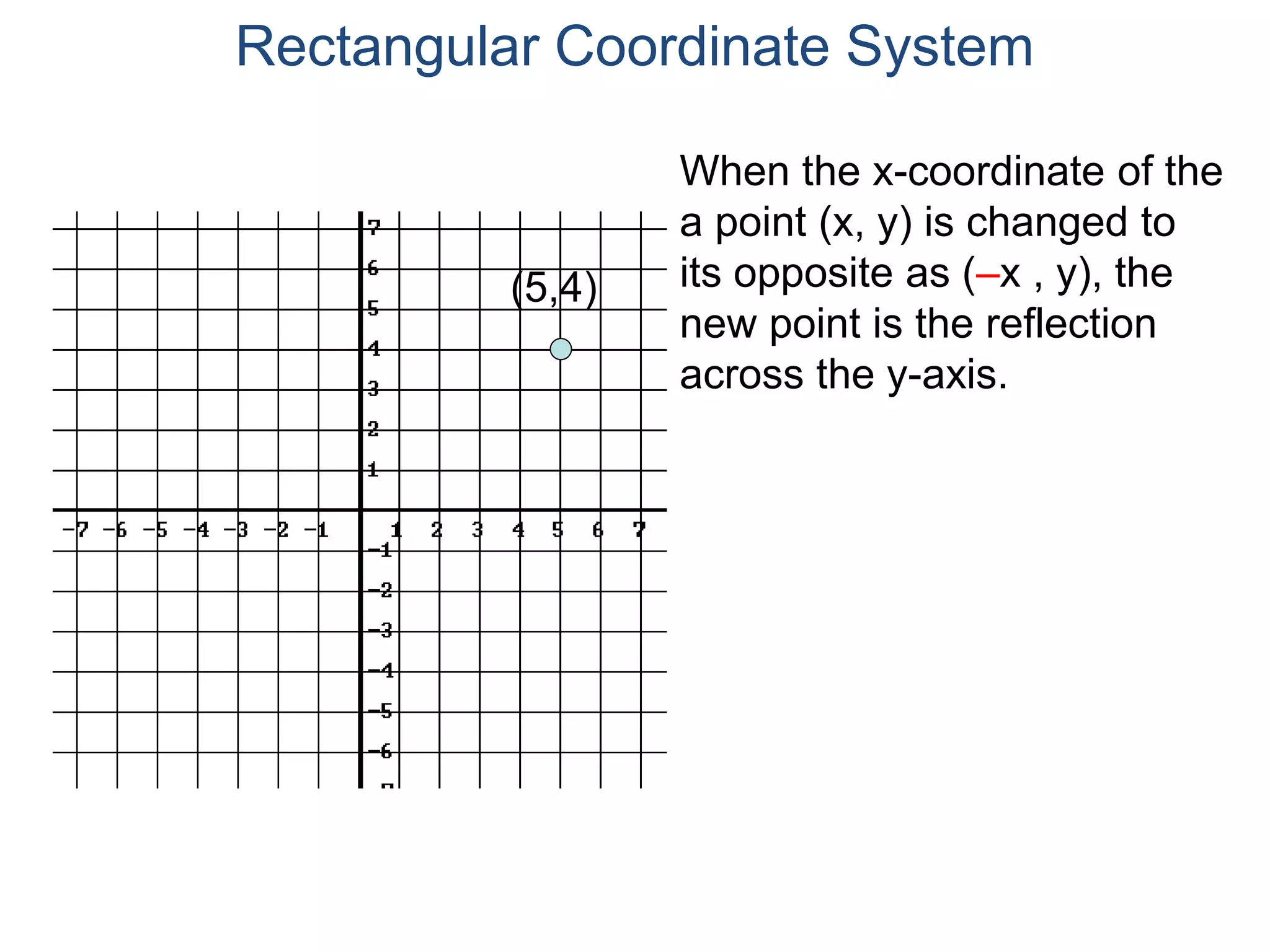
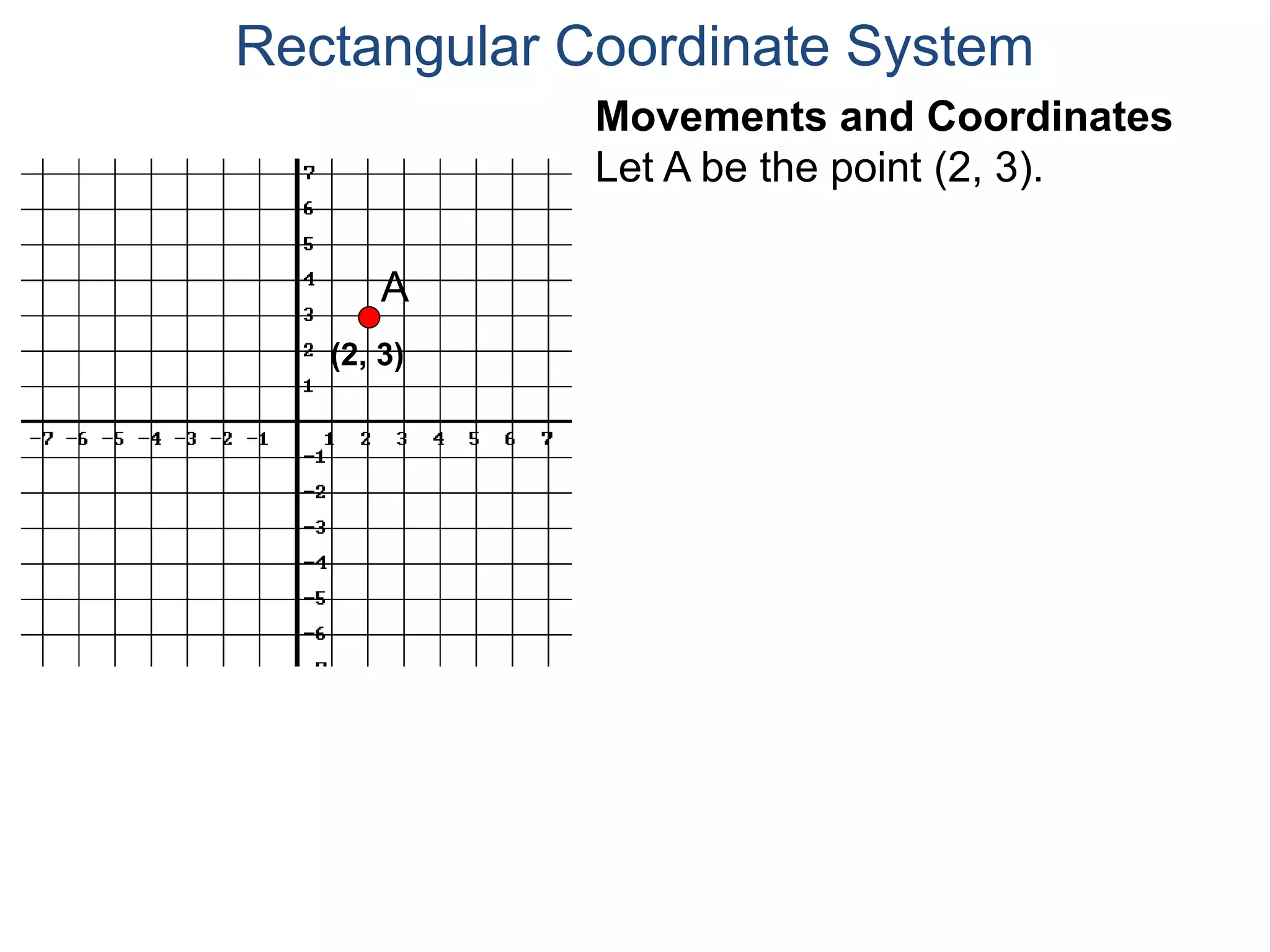
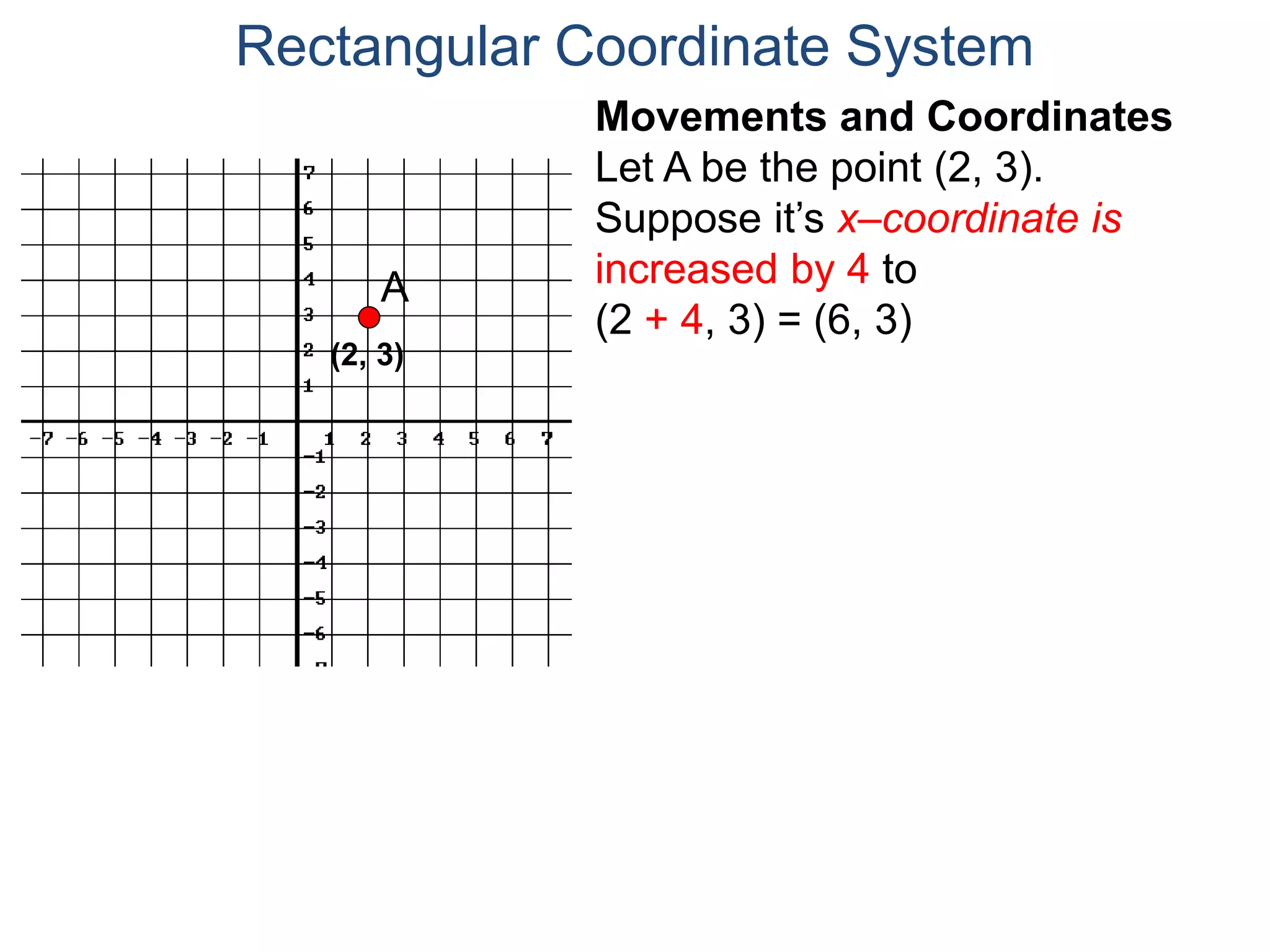
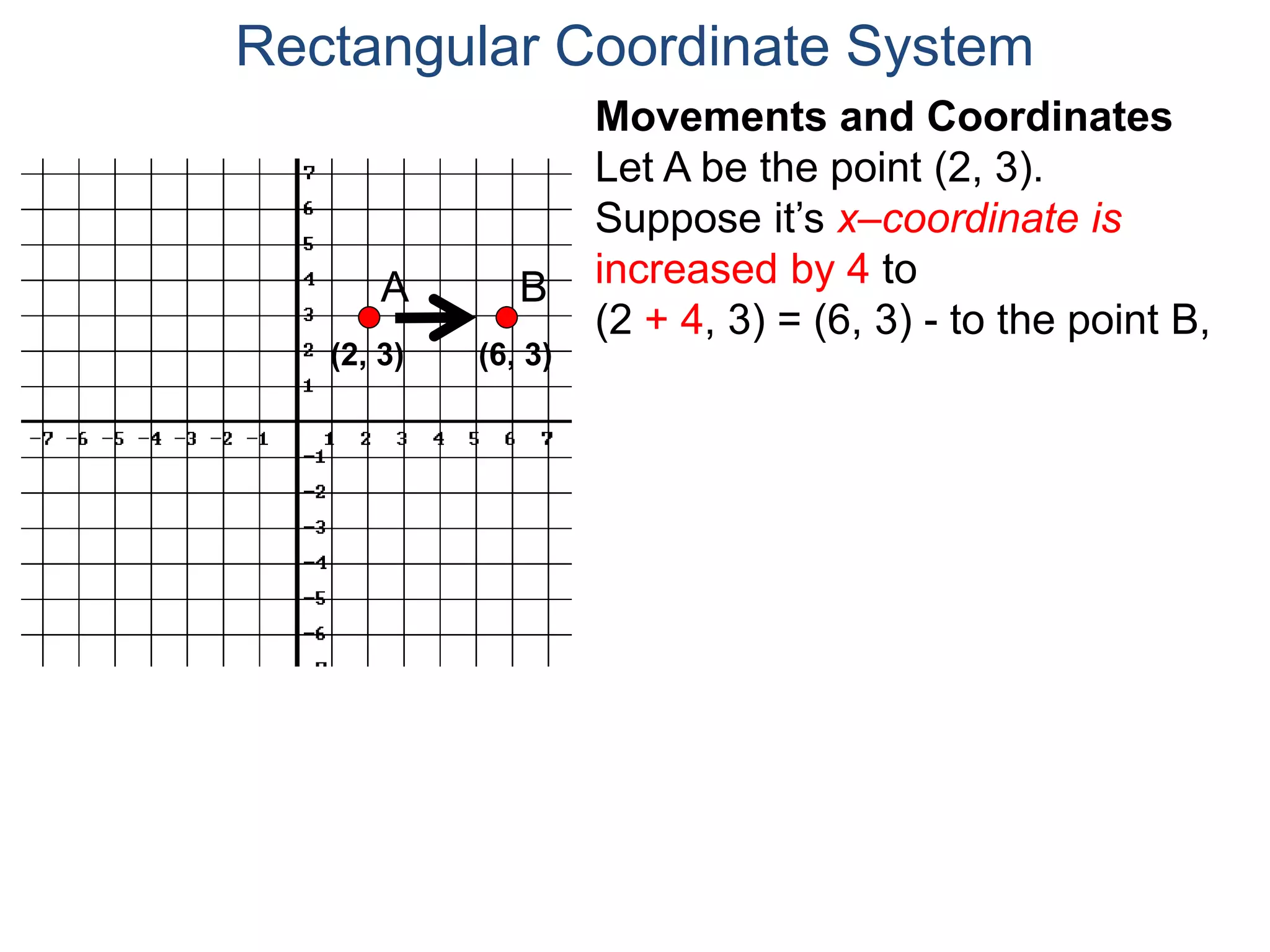
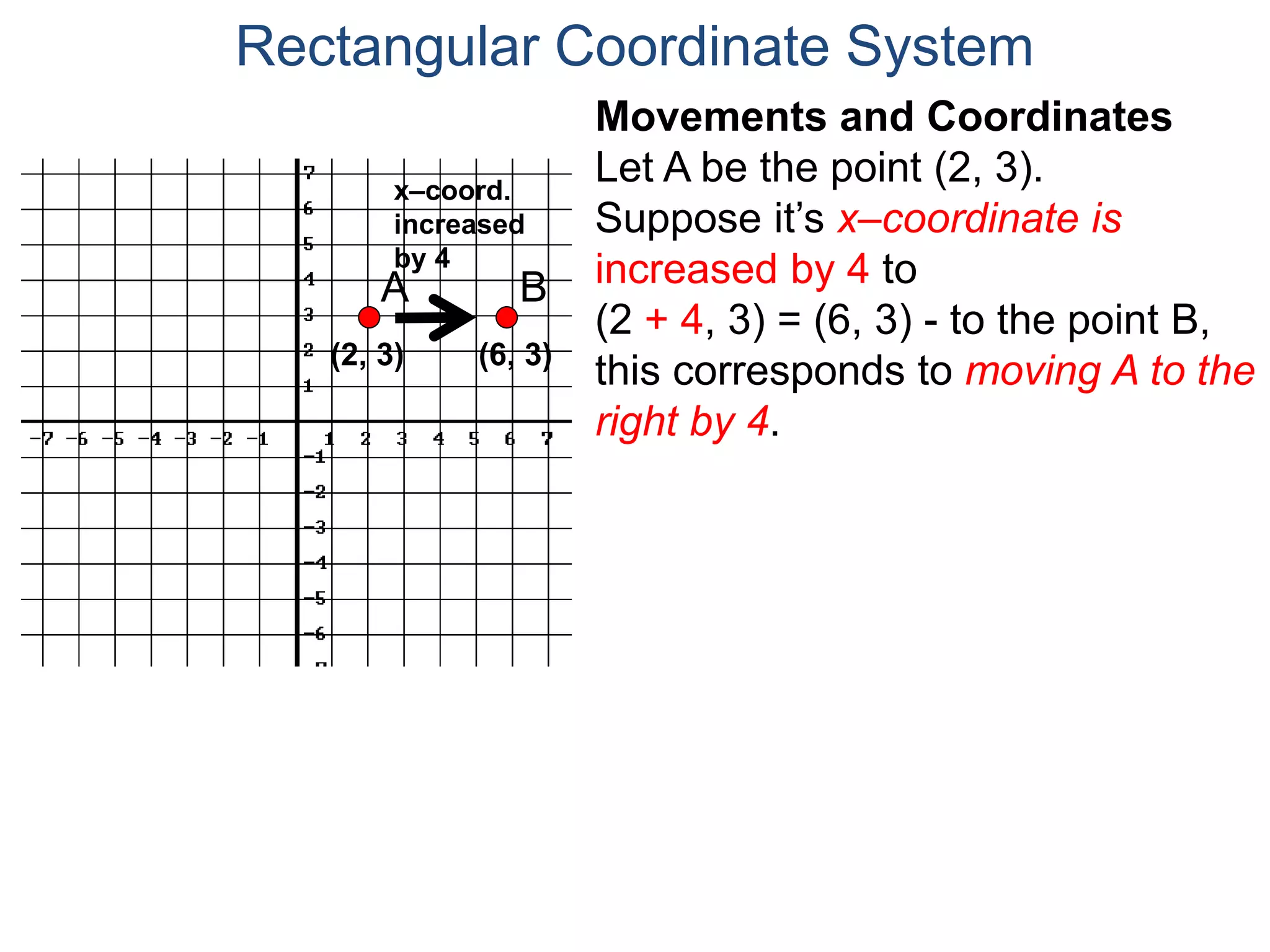
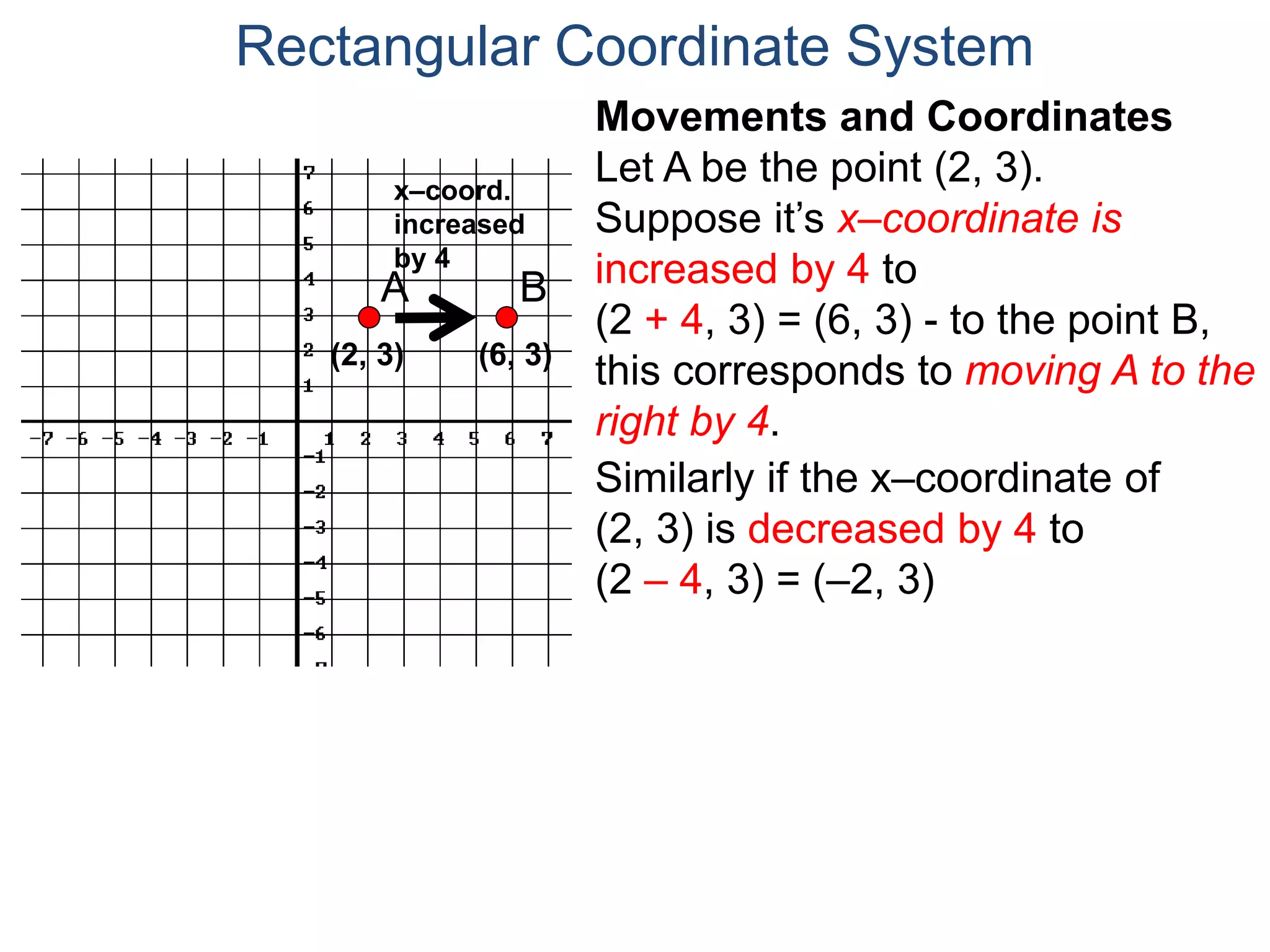
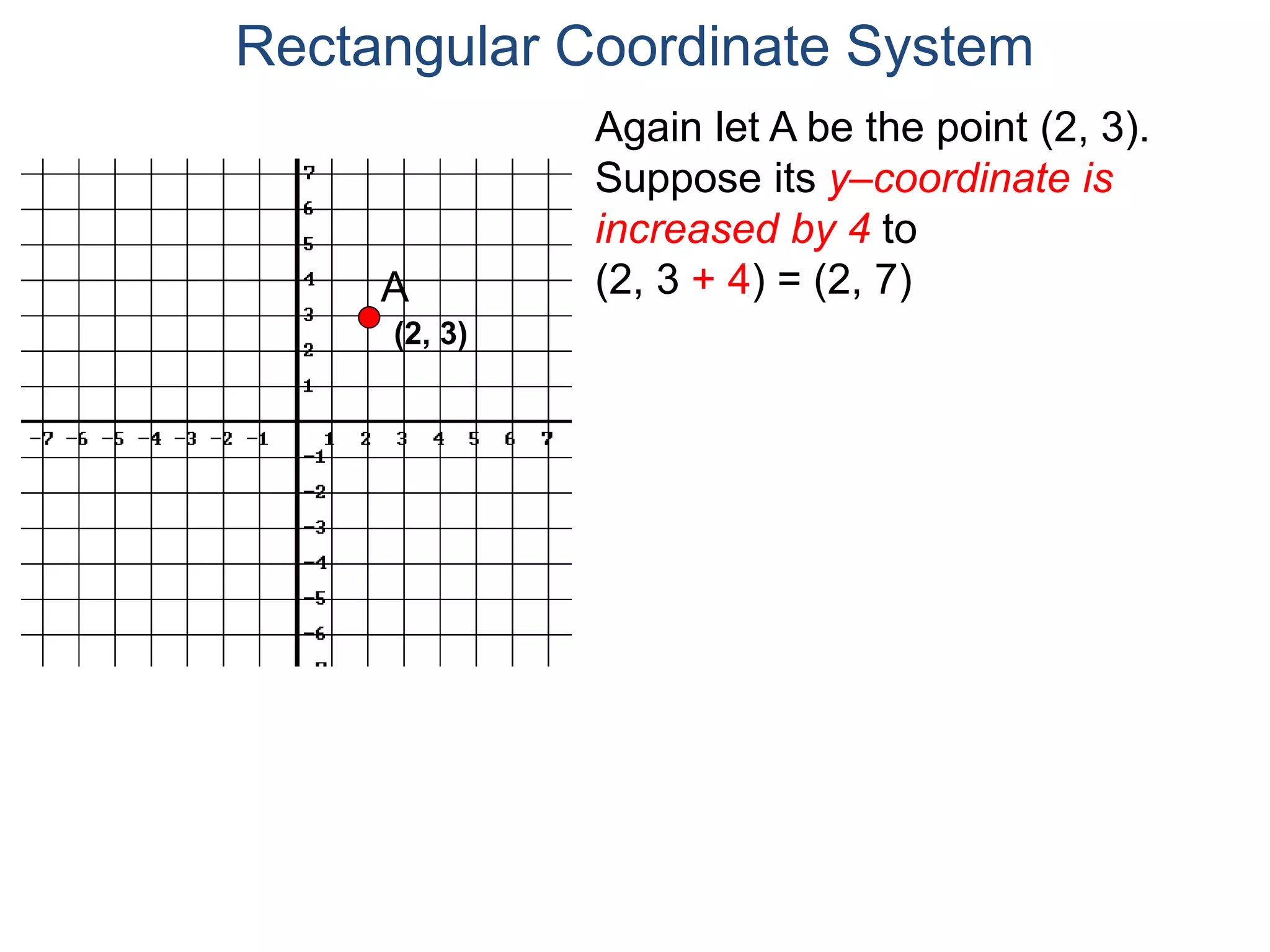
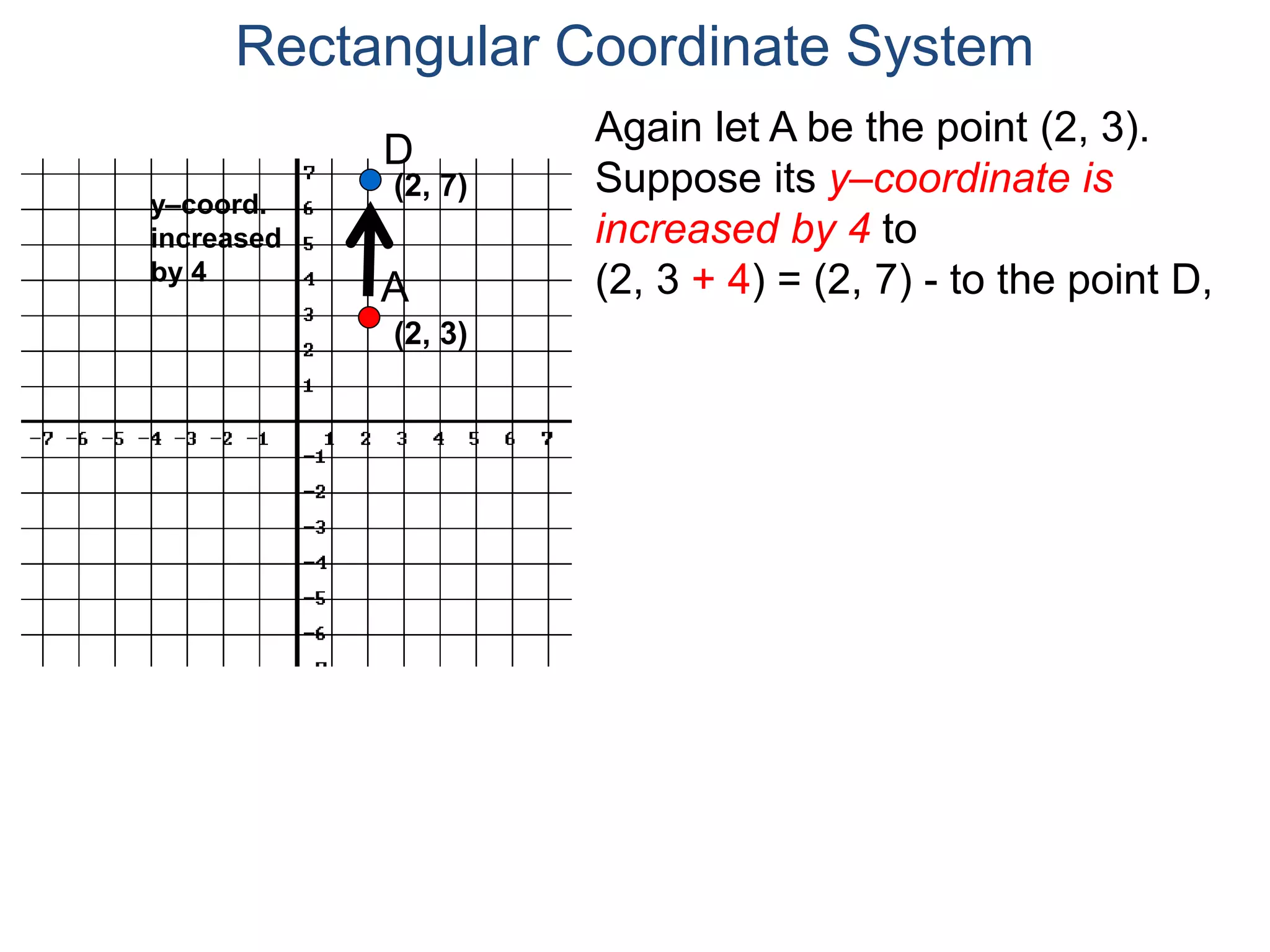
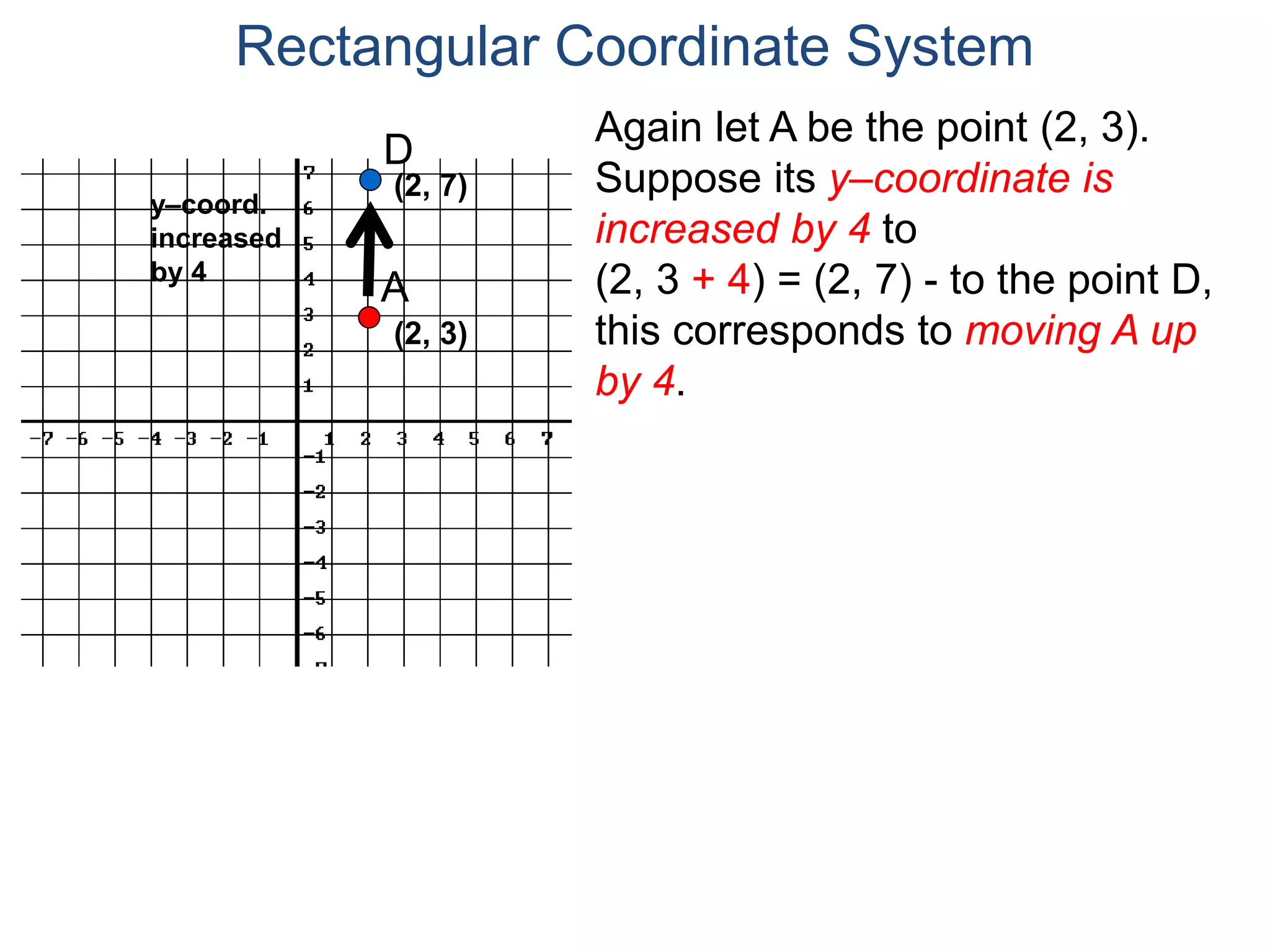
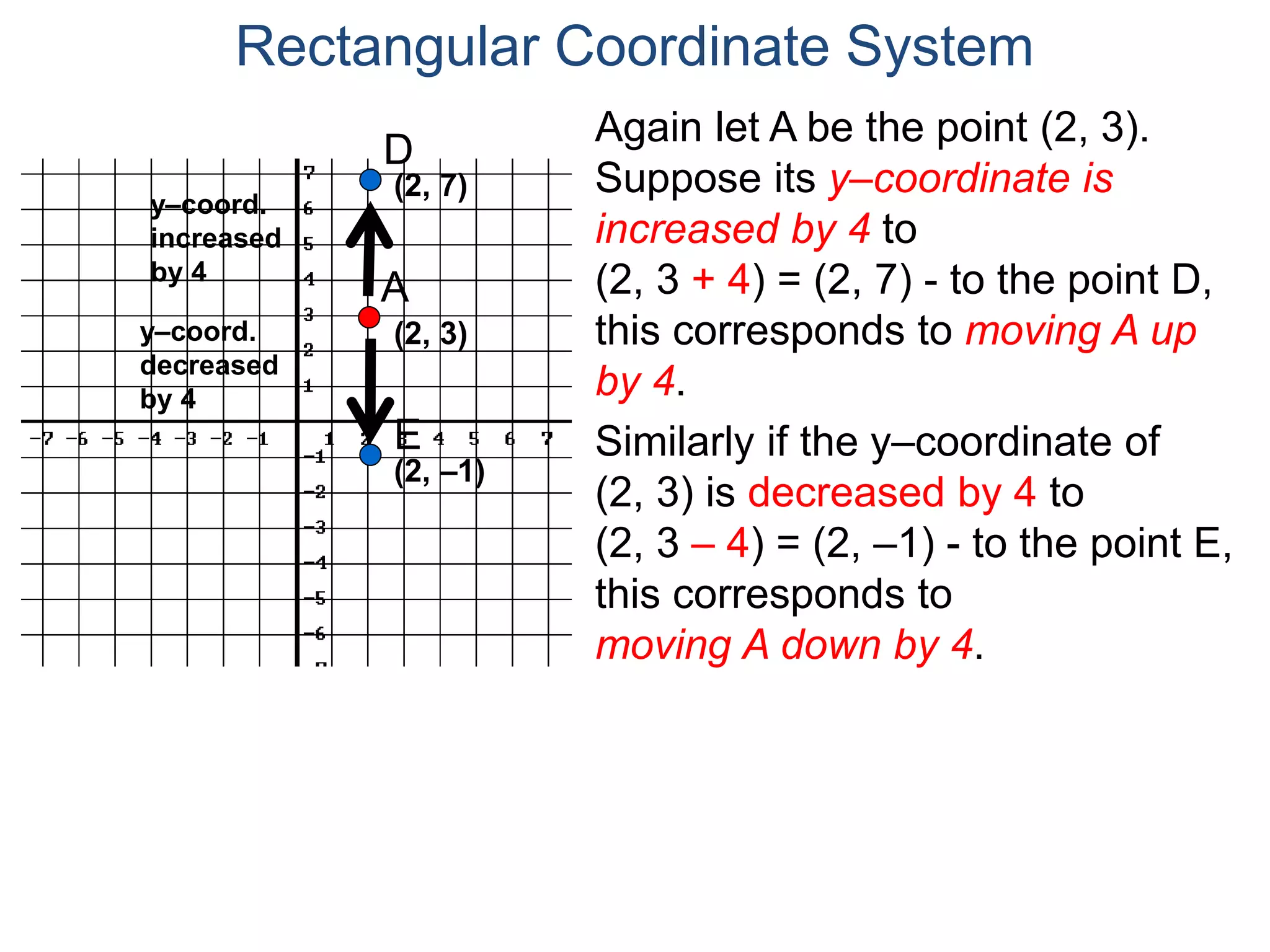
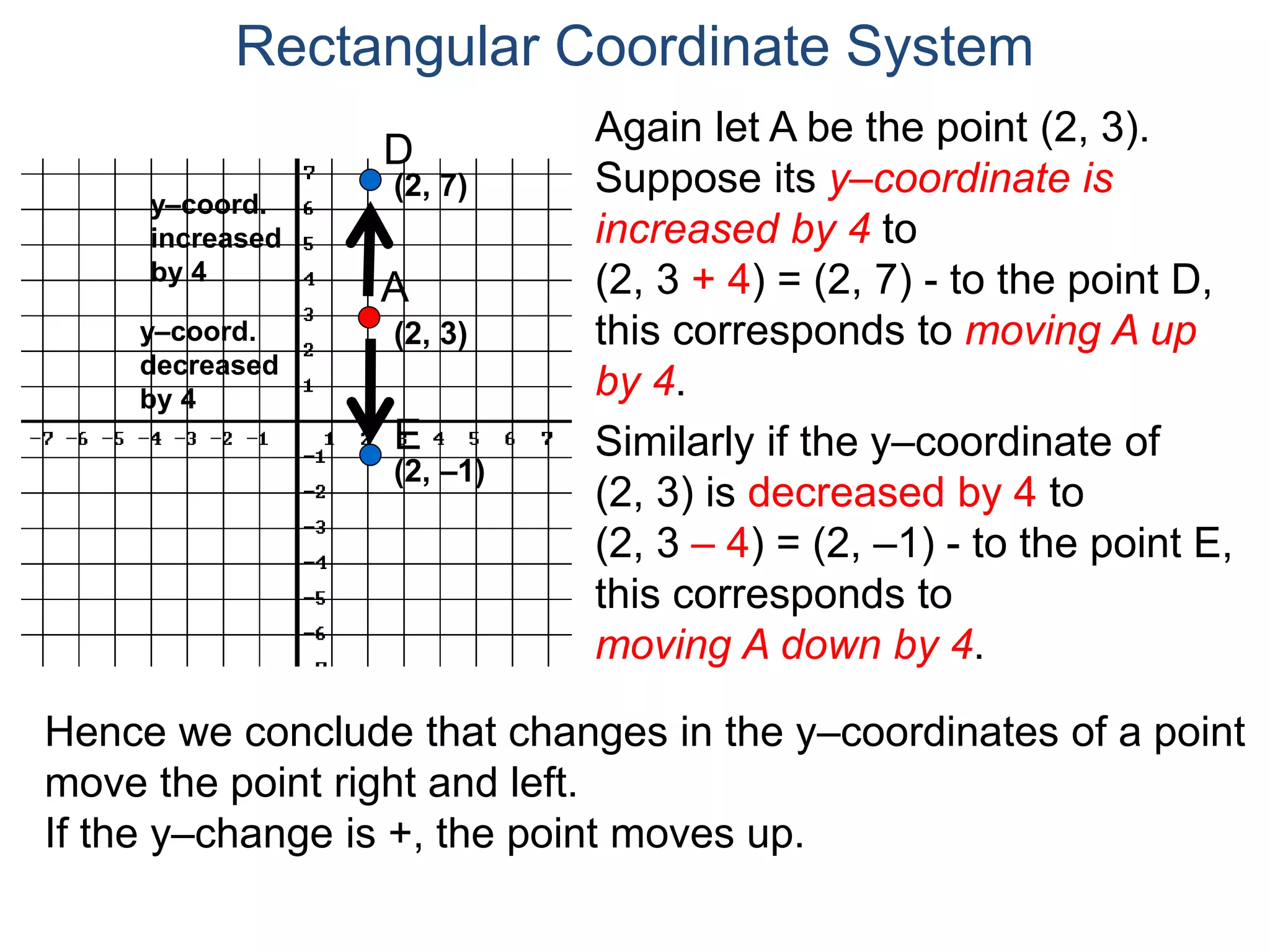
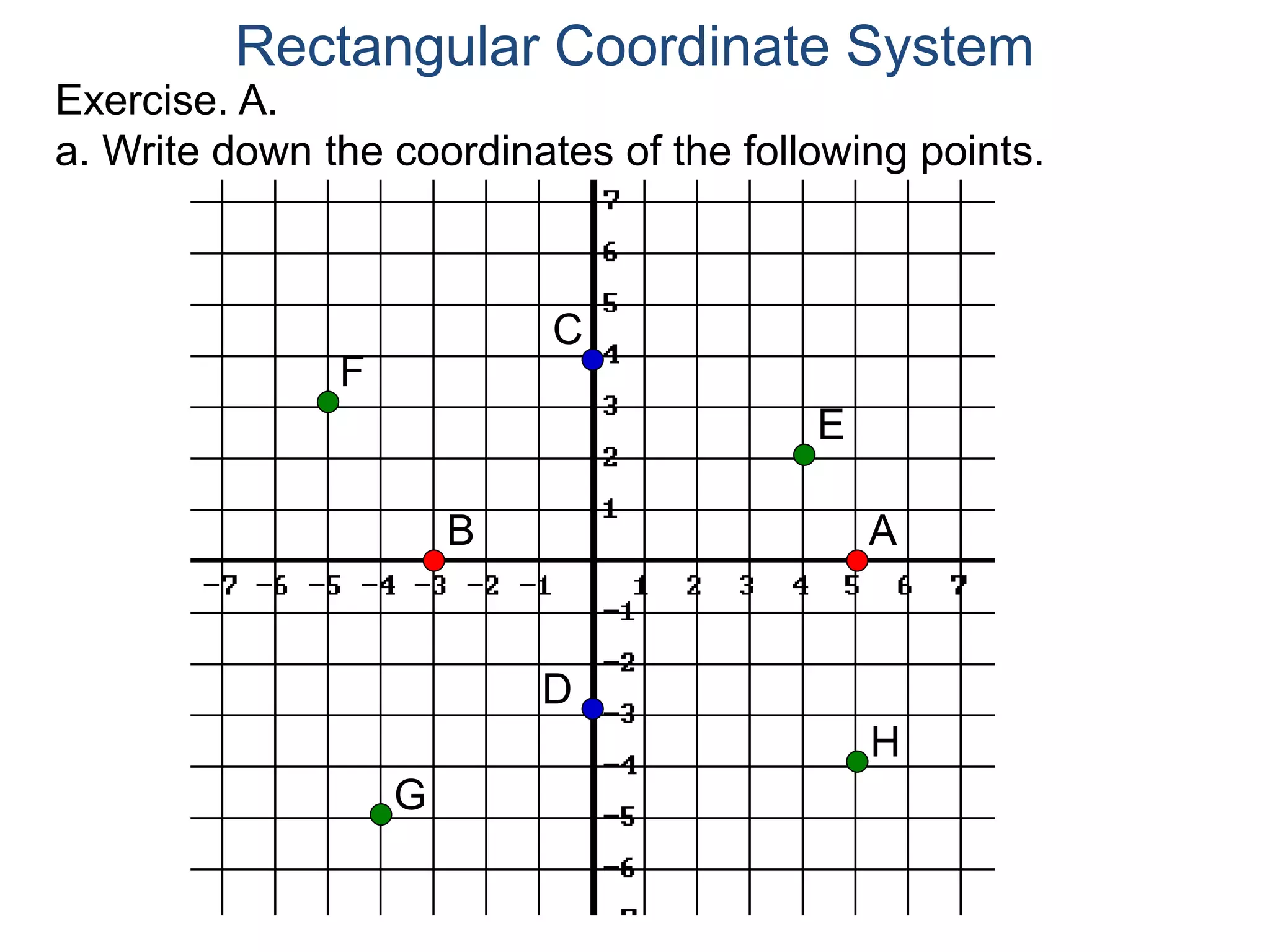
The document describes the rectangular coordinate system. It defines the system as using a grid with two perpendicular axes (x and y) that intersect at the origin (0,0). Any point in the plane can be located using its coordinates (x,y), where x is the distance from the y-axis and y is the distance from the x-axis. The four quadrants (I, II, III, IV) are defined by the intersection of the positive and negative sides of the x and y axes. Examples are given of labeling points and finding coordinates on the grid.

Embed presentation

Downloaded 41 times
Rectangular Coordinate System
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). Rectangular Coordinate System
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis.
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis.
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin.
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where:
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where: x = amount to move right (+) or left (–).
A coordinate system is a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where: x = amount to move right (+) or left (–). y = amount to move up (+) or down (–).
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). Rectangular Coordinate System
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) Rectangular Coordinate System
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, Rectangular Coordinate System
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System (4, –3) P
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5).
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A B
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A B C
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P Q R
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), P Q R
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), Q(3, -5), P Q R
x = amount to move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), Q(3, -5), R(-6, 0) P Q R
The coordinate of the origin is (0, 0). (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0) (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y).(0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y). (0, 6) (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y). (0, -4) (0, 6) (0,0) Rectangular Coordinate System
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV (+,+)
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV (+,+)(–,+)
The coordinate of the origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System Q1Q2 Q3 Q4 (+,+)(–,+) (–,–) (+,–) The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. Respectively, the signs of the coordinates of each quadrant are shown.
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. (5,4) Rectangular Coordinate System
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. (5,4)(–5,4) Rectangular Coordinate System
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) Rectangular Coordinate System
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) Rectangular Coordinate System
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) (–x, –y) is the reflection of (x, y) across the origin. Rectangular Coordinate System
When the x-coordinate of the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) (–x, –y) is the reflection of (x, y) across the origin. (–5, –4) Rectangular Coordinate System
Movements and Coordinates Rectangular Coordinate System
Movements and Coordinates Let A be the point (2, 3). Rectangular Coordinate System A (2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) Rectangular Coordinate System A (2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, Rectangular Coordinate System A B (2, 3) (6, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B x–coord. increased by 4 (2, 3) (6, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) x–coord. increased by 4 (2, 3) (6, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. If the x–change is +, the point moves to the right. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
Movements and Coordinates Let A be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. If the x–change is +, the point moves to the right. If the x–change is – , the point moves to the left. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
Again let A be the point (2, 3). Rectangular Coordinate System A (2, 3)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) Rectangular Coordinate System A (2, 3)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, Rectangular Coordinate System A D y–coord. increased by 4 (2, 3) (2, 7)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D y–coord. increased by 4 (2, 3) (2, 7)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. If the y–change is +, the point moves up. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
Again let A be the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. If the y–change is +, the point moves up. If the y–change is – , the point moves down. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A?
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate.
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4)
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4).
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A?
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate.
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100)
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104).
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A?
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right)
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down).
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down). Hence D has coordinate (–2 + 50, 4 – 30)
Rectangular Coordinate System Example. C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down). Hence D has coordinate (–2 + 50, 4 – 30) = (48, –26).
Exercise. A. a. Write down the coordinates of the following points. Rectangular Coordinate System AB C D E F G H
Ex. B. Plot the following points on the graph paper. Rectangular Coordinate System 2. a. (2, 0) b. (–2, 0) c. (5, 0) d. (–8, 0) e. (–10, 0) All these points are on which axis? 3. a. (0, 2) b. (0, –2) c. (0, 5) d. (0, –6) e. (0, 7) All these points are on which quadrant? 4. a. (5, 2) b. (2, 5) c. (1, 7) d. (7, 1) e. (6, 6) All these points are in which quadrant? 5. a. (–5, –2) b. (–2, –5) c. (–1, –7) d. (–7, –1) e. (–6, –6) All these points are in which quadrant? 6. List three coordinates whose locations are in the 2nd quadrant and plot them. 7. List three coordinates whose locations are in the 4th quadrant and plot them.
C. Find the coordinates of the following points. Draw both points for each problem. Rectangular Coordinate System The point that’s 8. 5 units to the right of (3, –2). 10. 4 units to the left of (–1, –5). 9. 6 units to the right of (–4, 2). 11. 6 units to the left of (2, –6). 12. 3 units to the left and 6 units down from (–2, 5). 13. 1 unit to the right and 5 units up from (–3, 1). 14. 3 units to the right and 3 units down from (–3, 4). 15. 2 units to the left and 6 units up from (4, –1).

More Related Content

PPTX
4 linear equations and graphs of lines
byelem-alg-sample
 
PPTX
3 1 rectangular coordinate system
bymath123a
 
PPTX
2.0 rectangular coordinate system
bymath260
 
PPTX
56 the rectangular coordinate system
byalg1testreview
 
PPTX
1 rectangular coordinate system x
byTzenma
 
PPTX
54 the rectangular coordinate system
byalg-ready-review
 
PPTX
3 5 rectangular system and lines-x
bymath123b
 
PPTX
59 constructing linea equations of lines
byalg1testreview
 
4 linear equations and graphs of lines
byelem-alg-sample
 
3 1 rectangular coordinate system
bymath123a
 
2.0 rectangular coordinate system
bymath260
 
56 the rectangular coordinate system
byalg1testreview
 
1 rectangular coordinate system x
byTzenma
 
54 the rectangular coordinate system
byalg-ready-review
 
3 5 rectangular system and lines-x
bymath123b
 
59 constructing linea equations of lines
byalg1testreview
 

What's hot

PPT
Parabola
byheiner gomez
 
PPT
27 triple integrals in spherical and cylindrical coordinates
bymath267
 
PPT
1 polar coordinates
bymath267
 
PPT
Coordinate geometry
byRavichandran Keerthi
 
PPTX
3 2 linear equations and lines
bymath123a
 
PPTX
57 graphing lines from linear equations
byalg1testreview
 
PPT
Lesson 8 conic sections - parabola
byJean Leano
 
PPT
Parabola complete
byMATOME PETER
 
PPT
1.2 the graphs of quadratic equations
bymath123c
 
PPTX
8 sign charts of factorable formulas y
bymath260
 
PPT
Parabola 091102134314-phpapp01
byA.
 
PPT
1576 parabola
byDr Fereidoun Dejahang
 
PPTX
Unit 13.2
byMark Ryder
 
DOCX
Conic sections
byindu psthakur
 
PPTX
Graphing parabola presentation
byVirgilio Paragele
 
PPTX
Lecture co2 math 21-1
byLawrence De Vera
 
PDF
Plotting of Points on the Coordinate Plane
byJoey Fontanilla Valdriz
 
PDF
Conic section
byTheepakorn Boonpleng
 
PPTX
22 the graphs of quadratic equations
bymath126
 
PPT
3.4 ellipses
bymath123c
 
Parabola
byheiner gomez
 
27 triple integrals in spherical and cylindrical coordinates
bymath267
 
1 polar coordinates
bymath267
 
Coordinate geometry
byRavichandran Keerthi
 
3 2 linear equations and lines
bymath123a
 
57 graphing lines from linear equations
byalg1testreview
 
Lesson 8 conic sections - parabola
byJean Leano
 
Parabola complete
byMATOME PETER
 
1.2 the graphs of quadratic equations
bymath123c
 
8 sign charts of factorable formulas y
bymath260
 
Parabola 091102134314-phpapp01
byA.
 
1576 parabola
byDr Fereidoun Dejahang
 
Unit 13.2
byMark Ryder
 
Conic sections
byindu psthakur
 
Graphing parabola presentation
byVirgilio Paragele
 
Lecture co2 math 21-1
byLawrence De Vera
 
Plotting of Points on the Coordinate Plane
byJoey Fontanilla Valdriz
 
Conic section
byTheepakorn Boonpleng
 
22 the graphs of quadratic equations
bymath126
 
3.4 ellipses
bymath123c
 

Viewers also liked

PPTX
Coordinate geometry
byAnju Soman
 
PPTX
Geometry (Grid & section formula)
byitutor
 
PPTX
Coordinate geometry
bySukhwinder Kumar
 
PPTX
Coordinate geometry
byErlyn Geronimo
 
PDF
co-ordinate systems
bySuganthi Thangaraj
 
PPT
Rectangular Coordinates, Introduction to Graphing Equations
bySandyPoinsett
 
PPT
Rectangular Coordinate System & Graphs
bymobart02
 
PPTX
MIT Math Syllabus 10-3 Lesson 3: Rational expressions
byLawrence De Vera
 
Coordinate geometry
byAnju Soman
 
Geometry (Grid & section formula)
byitutor
 
Coordinate geometry
bySukhwinder Kumar
 
Coordinate geometry
byErlyn Geronimo
 
co-ordinate systems
bySuganthi Thangaraj
 
Rectangular Coordinates, Introduction to Graphing Equations
bySandyPoinsett
 
Rectangular Coordinate System & Graphs
bymobart02
 
MIT Math Syllabus 10-3 Lesson 3: Rational expressions
byLawrence De Vera
 

Similar to 3 rectangular coordinate system

PPTX
10 rectangular coordinate system x
bymath260
 
PPTX
Coordinate System.pptx
byKeizylleCajeme
 
PDF
Computer Graphics - Cartesian Coordinate System.pdf
byAmol Gaikwad
 
PPT
3D Coordinate Geometry
byParasKulhari
 
PPTX
1 3 d coordinate system
bymath267
 
PPTX
The rectangular coordinate plane
byMartinGeraldine
 
PPTX
EMT_2A_cylindrical coordinates.pptx
by5610UmarIqbal
 
PPTX
powerpoint presentation MATATAG Curriculum pptx
byJessa Mae Vergara
 
PPTX
Coordinate goemetry
byRahul Nair
 
PPT
topic: rectangular coordinate system .ppt
bylandoyjennilyn
 
PPTX
Cartesian Coordinate System
byDARWINCRUZ24
 
PPTX
Axis system
byfa_coffeekate
 
PPTX
1 rectangular coordinate system x
byTzenma
 
PPTX
MATHEMATICS8 Q2 2. plot points on the Cartesian coordinate plane and determin...
byVernonSeanCorteza
 
PPTX
Mathematics8Lesson1CartesianPlanew1.pptx
byelmabethdelacruz1984
 
PPTX
Coordinate System.pptx
byKeizylleCajeme
 
PPTX
cartesian coordinate system fsgffgy.pptx
byAlfredCyrusRedulfin1
 
PDF
Astaño
byCire Oreja
 
PPTX
Christine
bychristine_25
 
PPTX
Christine
bychristine dayandante
 
10 rectangular coordinate system x
bymath260
 
Coordinate System.pptx
byKeizylleCajeme
 
Computer Graphics - Cartesian Coordinate System.pdf
byAmol Gaikwad
 
3D Coordinate Geometry
byParasKulhari
 
1 3 d coordinate system
bymath267
 
The rectangular coordinate plane
byMartinGeraldine
 
EMT_2A_cylindrical coordinates.pptx
by5610UmarIqbal
 
powerpoint presentation MATATAG Curriculum pptx
byJessa Mae Vergara
 
Coordinate goemetry
byRahul Nair
 
topic: rectangular coordinate system .ppt
bylandoyjennilyn
 
Cartesian Coordinate System
byDARWINCRUZ24
 
Axis system
byfa_coffeekate
 
1 rectangular coordinate system x
byTzenma
 
MATHEMATICS8 Q2 2. plot points on the Cartesian coordinate plane and determin...
byVernonSeanCorteza
 
Mathematics8Lesson1CartesianPlanew1.pptx
byelmabethdelacruz1984
 
Coordinate System.pptx
byKeizylleCajeme
 
cartesian coordinate system fsgffgy.pptx
byAlfredCyrusRedulfin1
 
Astaño
byCire Oreja
 
Christine
bychristine_25
 
Christine
bychristine dayandante
 

More from elem-alg-sample

PPTX
6 equations and applications of lines
byelem-alg-sample
 
PPTX
6 polynomial expressions and operations
byelem-alg-sample
 
PPTX
12 rational expressions
byelem-alg-sample
 
PPTX
3 linear equations
byelem-alg-sample
 
PPTX
11 applications of factoring
byelem-alg-sample
 
PPTX
4 literal equations
byelem-alg-sample
 
PPTX
13 multiplication and division of rational expressions
byelem-alg-sample
 
PPTX
18 variations
byelem-alg-sample
 
PPTX
17 applications of proportions and the rational equations
byelem-alg-sample
 
PPTX
10 more on factoring trinomials and factoring by formulas
byelem-alg-sample
 
PPTX
16 the multiplier method for simplifying complex fractions
byelem-alg-sample
 
PPTX
8 factoring out gcf
byelem-alg-sample
 
PPTX
2 the real line, inequalities and comparative phrases
byelem-alg-sample
 
PPTX
5 slopes of lines
byelem-alg-sample
 
PPTX
5 exponents and scientific notation
byelem-alg-sample
 
PPTX
9 factoring trinomials
byelem-alg-sample
 
PPTX
14 the lcm and the multiplier method for addition and subtraction of rational...
byelem-alg-sample
 
PPTX
7 special binomial operations and formulas
byelem-alg-sample
 
PPTX
15 proportions and the multiplier method for solving rational equations
byelem-alg-sample
 
PPTX
1 basic geometry and formulas
byelem-alg-sample
 
6 equations and applications of lines
byelem-alg-sample
 
6 polynomial expressions and operations
byelem-alg-sample
 
12 rational expressions
byelem-alg-sample
 
3 linear equations
byelem-alg-sample
 
11 applications of factoring
byelem-alg-sample
 
4 literal equations
byelem-alg-sample
 
13 multiplication and division of rational expressions
byelem-alg-sample
 
18 variations
byelem-alg-sample
 
17 applications of proportions and the rational equations
byelem-alg-sample
 
10 more on factoring trinomials and factoring by formulas
byelem-alg-sample
 
16 the multiplier method for simplifying complex fractions
byelem-alg-sample
 
8 factoring out gcf
byelem-alg-sample
 
2 the real line, inequalities and comparative phrases
byelem-alg-sample
 
5 slopes of lines
byelem-alg-sample
 
5 exponents and scientific notation
byelem-alg-sample
 
9 factoring trinomials
byelem-alg-sample
 
14 the lcm and the multiplier method for addition and subtraction of rational...
byelem-alg-sample
 
7 special binomial operations and formulas
byelem-alg-sample
 
15 proportions and the multiplier method for solving rational equations
byelem-alg-sample
 
1 basic geometry and formulas
byelem-alg-sample
 

Recently uploaded

PPTX
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
PDF
Analyzing the data of your initial survey
byThelma Villaflores
 
PDF
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
PPTX
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
PDF
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
PPTX
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
PDF
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 
PPTX
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
PPTX
Introduction-to-Anatomy-and-Physiology.pptx
byAshish Umale
 
PPTX
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
PDF
M.Sc. Nonchordates Complete Syllabus PPT | All Important Topics Covered
byKNIPSS SULTANPUR
 
PPTX
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
PPTX
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
PPTX
Access partner report in Odoo 18.2 _ Odoo 19
byCeline George
 
PDF
Scalable-MADDPG-Based Cooperative Target Invasion for a Multi-USV System.pdf
byMan_Ebook
 
PPTX
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
PPTX
ATTENTION -PART 2.pptx Shilpa Hotakar for I semester BSc students
bySHILPA HOTAKAR
 
PPTX
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
PPTX
REVISED DEFENSE MECHANISM / ADJUSTMENT MECHANISM-FINAL
byShimla
 
PPTX
4 G8_Q3_L4 (Evaluating opinion editorials for textual evidence and quality).pptx
byNorafeSahagun
 
10-12-2025 Francois Staring How can Researchers and Initial Teacher Educators...
byEduSkills OECD
 
Analyzing the data of your initial survey
byThelma Villaflores
 
Most Imp Chapters & Weightage for Boards 2025.pdf
byTamannaSagar
 
Partial Correlation of Coefficient - Values of r₁₂.₃, r₂₃.₁ & r₁₃.₂
bySundar B N
 
Using Charts and Tables in Presenting Data
byThelma Villaflores
 
Accounting Skills Paper-II (Registers of PACs and Credit Co-operative Societies)
byDr. Sushil Bansode
 
Blood Group Incompatibility: Rh Factor and Erythroblastosis Fetalis
bySudhandraKarthi
 
Basics in Phytochemistry, Extraction, Isolation methods, Characterisation etc.
byD. Y. Patil College of Pharmacy, Kolhapur.
 
Introduction-to-Anatomy-and-Physiology.pptx
byAshish Umale
 
AN EXTREMELY BORING GENERAL QUIZ FOR UG.pptx
bySriramG47
 
M.Sc. Nonchordates Complete Syllabus PPT | All Important Topics Covered
byKNIPSS SULTANPUR
 
PURPOSIVE SAMPLING IN EDUCATIONAL RESEARCH RACHITHRA RK.pptx
byssuser047b711
 
Repeat Orders_ Use Odoo Blanket Agreement
byCeline George
 
Access partner report in Odoo 18.2 _ Odoo 19
byCeline George
 
Scalable-MADDPG-Based Cooperative Target Invasion for a Multi-USV System.pdf
byMan_Ebook
 
Steve Hale - Developing Elite Young Goalkeepers 2024.pptx
bypjmfd
 
ATTENTION -PART 2.pptx Shilpa Hotakar for I semester BSc students
bySHILPA HOTAKAR
 
Semester 6 Unit 2 Club foot (talipes).pptx
bysachin7989
 
REVISED DEFENSE MECHANISM / ADJUSTMENT MECHANISM-FINAL
byShimla
 
4 G8_Q3_L4 (Evaluating opinion editorials for textual evidence and quality).pptx
byNorafeSahagun
 

3 rectangular coordinate system

  • 1.
  • 2.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). Rectangular Coordinate System
  • 3.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System
  • 4.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System
  • 5.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis.
  • 6.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis.
  • 7.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin.
  • 8.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where:
  • 9.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where: x = amount to move right (+) or left (–).
  • 10.
    A coordinate systemis a system of assigning addresses for positions in the plane (2 D) or in space (3 D). The rectangular coordinate system for the plane consists of a rectangular grid where each point in the plane is addressed by an ordered pair of numbers (x, y). Rectangular Coordinate System The horizontal axis is called the x-axis. The vertical axis is called the y-axis. The point where the axes meet is called the origin. Starting from the origin, each point is addressed by its ordered pair (x, y) where: x = amount to move right (+) or left (–). y = amount to move up (+) or down (–).
  • 11.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). Rectangular Coordinate System
  • 12.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) Rectangular Coordinate System
  • 13.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, Rectangular Coordinate System
  • 14.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System (4, –3) P
  • 15.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5).
  • 16.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A
  • 17.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A B
  • 18.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). A B C
  • 19.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C
  • 20.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P Q R
  • 21.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), P Q R
  • 22.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), Q(3, -5), P Q R
  • 23.
    x = amountto move right (+) or left (–). y = amount to move up (+) or down (–). For example, the point P corresponds to (4, –3) is 4 right, and 3 down from the origin. Rectangular Coordinate System Example A. Label the points A(-1, 2), B(-3, -2),C(0, -5). The ordered pair (x, y) corresponds to a point is called the coordinate of the point, x is the x-coordinate and y is the y-coordinate. A B C Example B: Find the coordinate of P, Q, R as shown. P(4, 5), Q(3, -5), R(-6, 0) P Q R
  • 24.
    The coordinate ofthe origin is (0, 0). (0,0) Rectangular Coordinate System
  • 25.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (0,0) Rectangular Coordinate System
  • 26.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0) (0,0) Rectangular Coordinate System
  • 27.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) (0,0) Rectangular Coordinate System
  • 28.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y).(0,0) Rectangular Coordinate System
  • 29.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y). (0, 6) (0,0) Rectangular Coordinate System
  • 30.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). (5, 0)(-6, 0) Any point on the y-axis has coordinate of the form (0, y). (0, -4) (0, 6) (0,0) Rectangular Coordinate System
  • 31.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV
  • 32.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV (+,+)
  • 33.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. QIQII QIII QIV (+,+)(–,+)
  • 34.
    The coordinate ofthe origin is (0, 0). Any point on the x-axis has coordinate of the form (x, 0). Any point on the y-axis has coordinate of the form (0, y). Rectangular Coordinate System Q1Q2 Q3 Q4 (+,+)(–,+) (–,–) (+,–) The axes divide the plane into four parts. Counter clockwise, they are denoted as quadrants I, II, III, and IV. Respectively, the signs of the coordinates of each quadrant are shown.
  • 35.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. (5,4) Rectangular Coordinate System
  • 36.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. (5,4)(–5,4) Rectangular Coordinate System
  • 37.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) Rectangular Coordinate System
  • 38.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) Rectangular Coordinate System
  • 39.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) (–x, –y) is the reflection of (x, y) across the origin. Rectangular Coordinate System
  • 40.
    When the x-coordinateof the a point (x, y) is changed to its opposite as (–x , y), the new point is the reflection across the y-axis. When the y-coordinate of the a point (x, y) is changed to its opposite as (x , –y), the new point is the reflection across the x-axis. (5,4)(–5,4) (5, –4) (–x, –y) is the reflection of (x, y) across the origin. (–5, –4) Rectangular Coordinate System
  • 41.
  • 42.
    Movements and Coordinates LetA be the point (2, 3). Rectangular Coordinate System A (2, 3)
  • 43.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) Rectangular Coordinate System A (2, 3)
  • 44.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, Rectangular Coordinate System A B (2, 3) (6, 3)
  • 45.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B x–coord. increased by 4 (2, 3) (6, 3)
  • 46.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) x–coord. increased by 4 (2, 3) (6, 3)
  • 47.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
  • 48.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
  • 49.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
  • 50.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. If the x–change is +, the point moves to the right. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
  • 51.
    Movements and Coordinates LetA be the point (2, 3). Suppose it’s x–coordinate is increased by 4 to (2 + 4, 3) = (6, 3) - to the point B, this corresponds to moving A to the right by 4. Rectangular Coordinate System A B Similarly if the x–coordinate of (2, 3) is decreased by 4 to (2 – 4, 3) = (–2, 3) - to the point C, this corresponds to moving A to the left by 4. Hence we conclude that changes in the x–coordinates of a point move the point right and left. If the x–change is +, the point moves to the right. If the x–change is – , the point moves to the left. C x–coord. increased by 4 x–coord. decreased by 4 (2, 3) (6, 3)(–2, 3)
  • 52.
    Again let Abe the point (2, 3). Rectangular Coordinate System A (2, 3)
  • 53.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) Rectangular Coordinate System A (2, 3)
  • 54.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, Rectangular Coordinate System A D y–coord. increased by 4 (2, 3) (2, 7)
  • 55.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D y–coord. increased by 4 (2, 3) (2, 7)
  • 56.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
  • 57.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
  • 58.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
  • 59.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. If the y–change is +, the point moves up. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
  • 60.
    Again let Abe the point (2, 3). Suppose its y–coordinate is increased by 4 to (2, 3 + 4) = (2, 7) - to the point D, this corresponds to moving A up by 4. Rectangular Coordinate System A D Similarly if the y–coordinate of (2, 3) is decreased by 4 to (2, 3 – 4) = (2, –1) - to the point E, this corresponds to moving A down by 4. Hence we conclude that changes in the y–coordinates of a point move the point right and left. If the y–change is +, the point moves up. If the y–change is – , the point moves down. E y–coord. increased by 4 y–coord. decreased by 4 (2, 3) (2, 7) (2, –1)
  • 61.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A?
  • 62.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate.
  • 63.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4)
  • 64.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4).
  • 65.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A?
  • 66.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate.
  • 67.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100)
  • 68.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104).
  • 69.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A?
  • 70.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right)
  • 71.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down).
  • 72.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down). Hence D has coordinate (–2 + 50, 4 – 30)
  • 73.
    Rectangular Coordinate System Example.C. a. Let A be the point (–2, 4). What is the coordinate of the point B that is 100 units directly left of A? Moving left corresponds to decreasing the x-coordinate. Hence B is (–2 – 100, 4) = (–102, 4). b. What is the coordinate of the point C that is 100 units directly above A? Moving up corresponds to increasing the y-coordinate. Hence C is (–2, 4) = (–2, 4 +100) = (–2, 104). c. What is the coordinate of the point D that is 50 to the right and 30 below A? We need to add 50 to the x–coordinate (to the right) and subtract 30 from the y–coordinate (to go down). Hence D has coordinate (–2 + 50, 4 – 30) = (48, –26).
  • 74.
    Exercise. A. a. Writedown the coordinates of the following points. Rectangular Coordinate System AB C D E F G H
  • 75.
    Ex. B. Plotthe following points on the graph paper. Rectangular Coordinate System 2. a. (2, 0) b. (–2, 0) c. (5, 0) d. (–8, 0) e. (–10, 0) All these points are on which axis? 3. a. (0, 2) b. (0, –2) c. (0, 5) d. (0, –6) e. (0, 7) All these points are on which quadrant? 4. a. (5, 2) b. (2, 5) c. (1, 7) d. (7, 1) e. (6, 6) All these points are in which quadrant? 5. a. (–5, –2) b. (–2, –5) c. (–1, –7) d. (–7, –1) e. (–6, –6) All these points are in which quadrant? 6. List three coordinates whose locations are in the 2nd quadrant and plot them. 7. List three coordinates whose locations are in the 4th quadrant and plot them.
  • 76.
    C. Find thecoordinates of the following points. Draw both points for each problem. Rectangular Coordinate System The point that’s 8. 5 units to the right of (3, –2). 10. 4 units to the left of (–1, –5). 9. 6 units to the right of (–4, 2). 11. 6 units to the left of (2, –6). 12. 3 units to the left and 6 units down from (–2, 5). 13. 1 unit to the right and 5 units up from (–3, 1). 14. 3 units to the right and 3 units down from (–3, 4). 15. 2 units to the left and 6 units up from (4, –1).