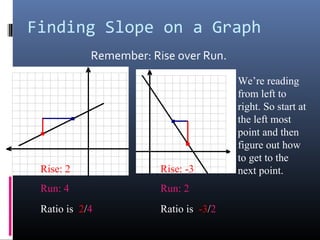
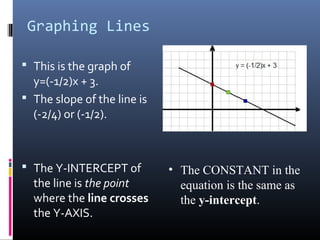
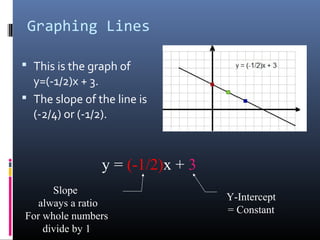
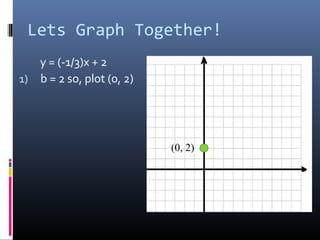
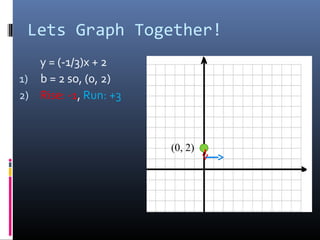
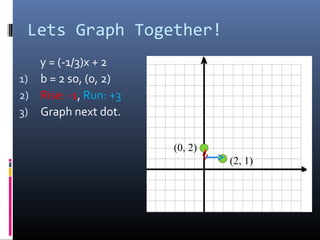
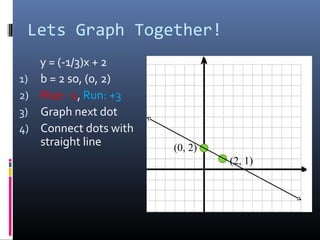
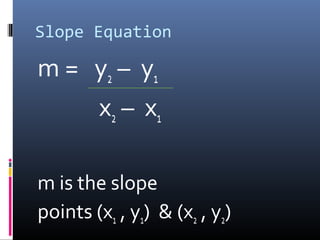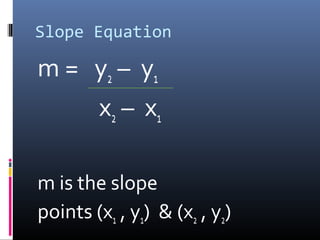The document provides a comprehensive review of slope concepts from Algebra I, including how to calculate slope using the formula, identifying positive and negative slopes, and understanding special cases for horizontal and vertical lines. It also covers the formats for linear equations and how to graph them using the slope-intercept form, as well as finding parallel and perpendicular lines based on their slopes. Additionally, practice problems are suggested to reinforce these concepts.

1. Review of slope from Algebra I
Graphing lines of a known slope and intercept

2. Slope Review from Algebra I

3. Slope
 The ratio that describes the tilt of a line is its
slope.
 To calculate slope, you use this ratio.
 Slope = (Vertical Change) = Rise
(Horizontal Change) Run

4. Slope Equation
m = y2 – y 1
x 2 – x1
m is the slope
points (x1 , y1) & (x2 , y2)

5. Slope
 A positive slope rises to the right
 A negative slope falls to the right

6. Finding Slope on a Graph
Remember: Rise over Run.
We’re reading
from left to
right. So start at
the left most
point and then
figure out how
to get to the
Rise: 2 Rise: -3 next point.
Run: 4 Run: 2
Ratio is 2/4 Ratio is -3/2

7. Finding Slope from 2 Points
 You can find the slope of the line using the
ratio.
 slope = difference of y – coordinates
difference of x – coordinates.
 The y-coordinate you use first in the
numerator must correspond to the x-
coordinate you use first in the denominator.

8. Slope Equation
m = y2 – y 1
x 2 – x1
m is the slope
points (x1 , y1) & (x2 , y2)

9. Find the slope of the line
through C(-2, 6) and D(4,
3) = difference in y-coordinates
Slope
difference in x-coordinates
= (3 – 6)  y-coordinates
(4 – (-2))  x-coordinates
Slope = -3 / 6 = -1/2
Down 1, to the Right 2. Cause of Rise (of –1)
over Run (+2).

10. Find the Slope of the Line
through each pair of
points:
 V(8, -1) and Q(0, -7)
 S(-4, 3) and R(-10, 9)

11. Find the Slope of the Line
through each pair of
points:
 V(8, -1) and Q(0, -7)
m = 3/4
 S(-4, 3) and R(-10, 9)
m = -1
= (-1 / 1) if you need a ratio

12. Special Cases
 Horizontal and Vertical lines are special cases
This is a horizontal line.
The points are (-3, 2) and (1, 2).
Therefore, Y = 2.
Find the slope.
Slope = (2 – 2) / (1 – (-3) = 0 /4 = 0
The slope for a horizontal line (or anything Y = ?) is zero.

13. Special Cases
 Horizontal and Vertical lines are special cases
This is a vertical line.
The points are (-4, 1) and (-4, 3).
Therefore, X = -4.
Find the slope.
Slope = (1 – 3) / (-4 – (-4) = -2 /0 = Undefined
Slope is, therefore, UNDEFINED for vertical lines.
lines

14. Finding the Equation of a Line

15. Formats for a Linear
Equation
 Standard Form: ax + by = c
 Slope-Intercept : y = mx + b
 Use your properties of algebra to convert
between the two
(Addition Property, Division Property, etc)

16. Finding the Equation of a
Line
 Use your slope equation with any point on the
line and the point (x, y)
 For example the points C(-2, 6) and D(4, 3)
earlier had a slope of -1/2
 m = y2 – y1 -1 = y – 6
x2 – x 1 2 x – (-2)
2( y-6 ) = -1 ( x – (-2) )
2y - 12 = -x +2
y = (-1/2) x + 7

17. Graphing Lines

18. Graphing Lines
 This is the graph of
y=(-1/2)x + 3.
 The slope of the line is
(-2/4) or (-1/2).
 The Y-INTERCEPT of • The CONSTANT in the
the line is the point equation is the same as
where the line crosses the y-intercept.
the Y-AXIS.

19. Graphing Lines
 This is the graph of
y=(-1/2)x + 3.
 The slope of the line is
(-2/4) or (-1/2).
y = (-1/2)x + 3
Slope
Y-Intercept
always a ratio
= Constant
For whole numbers
divide by 1

20. Using Slope-Intercept Form
 Using the Slope-Intercept Form, you can
graph without having to pick points and make
a table.
y = mx + b Slope-Intercept Form
 m = Slope of the line. (Ratio)
 b = Y-Intercept. (Constant)
 Linear Equations can always be put in this
format. It is like solving for y.

21. To Graph with y = mx + b
1) Start with b. Since b is where the line of the
equation hits the y-axis, its your first point.
Point = (0, b)
2) Take the slope, or m. Starting at b, move
along the RISE and RUN of the ratio.
3) Where you end up is your second point.
4) Connect the two dots with a line. (This is the
graph of your linear equation).

22. Lets Graph Together!
y = (-1/3)x + 2

23. Lets Graph Together!
y = (-1/3)x + 2
1) b = 2 so, plot (0, 2)
(0, 2)

24. Lets Graph Together!
y = (-1/3)x + 2
1) b = 2 so, (0, 2)
2) Rise: -1, Run: +3
(0, 2)

25. Lets Graph Together!
y = (-1/3)x + 2
1) b = 2 so, (0, 2)
2) Rise: -1, Run: +3
3) Graph next dot.
(0, 2)
(2, 1)

26. Lets Graph Together!
y = (-1/3)x + 2
1) b = 2 so, (0, 2)
2) Rise: -1, Run: +3
3) Graph next dot
4) Connect dots with
straight line (0, 2)
(2, 1)

27. Finding Parallel and
Perpendicular Lines

28. Parallel Lines
 Parallel lines have the same slope
 Find the equation using the same process we
used above with the slope and the new point

29. Example of Parallel Line
 Find a line parallel to y = (-1/2)x + 7 through
point ( 10, 3)
 -1 = y – 3
2 x – 10
2(y – 3) = -1 (x – 10) Cross multiplied
2y – 6 = -x + 10 Distributive Property
2y = -x +16 Added 6 to both sides
y = (-1/2)x + 8 Divided by 2

30. Perpendicular Line
 The slope of a perpendicular line is the
negative inverse of the original slope
 For example, if the original slope is -1/2, the
perpendicular slope is 2 (Ratio form 2/1)
 To find a perpendicular line through a given
point, use the perpendicular slope and the
given point in the slope equation

31. Example of Perpendicular
Line
 Find a line perpendicular to y = (-1/2)x + 7
through point ( 10, 3)
 Perpendicular slope = 2 (same as 2 / 1 )
2 = y–3 Slope equation
1 x – 10
1 (y – 3) = 2 (x – 10) Cross multiplied
y – 3 = 2x - 20 Distributive Property
y = 2x - 17 Added 3 to both sides

32. Practice
 Even problems in the sets below
 Textbook p168: even of (12-18, 24, 34-42)
 Textbook p175: even of (8-16, 24-32, 38-44)