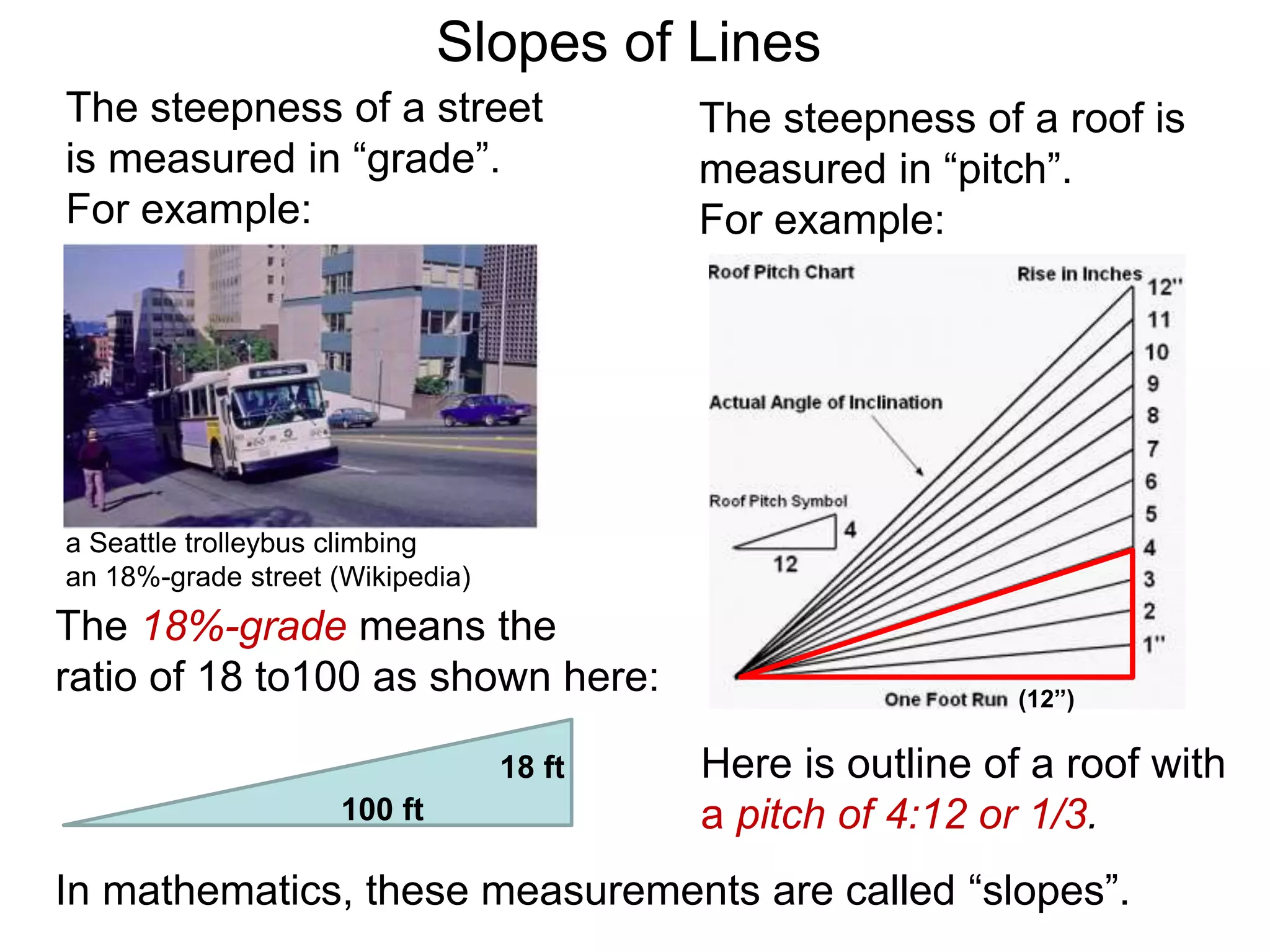
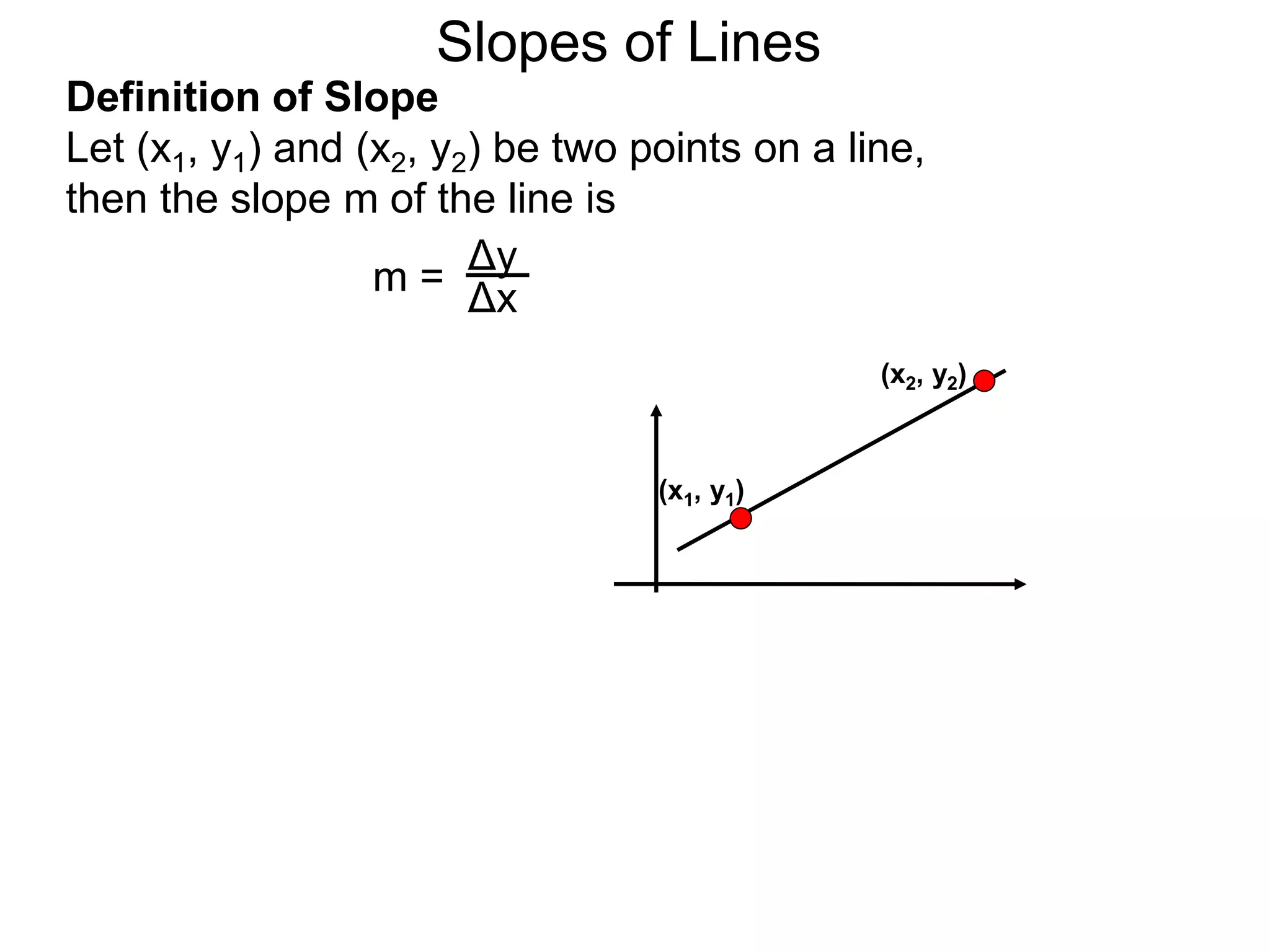
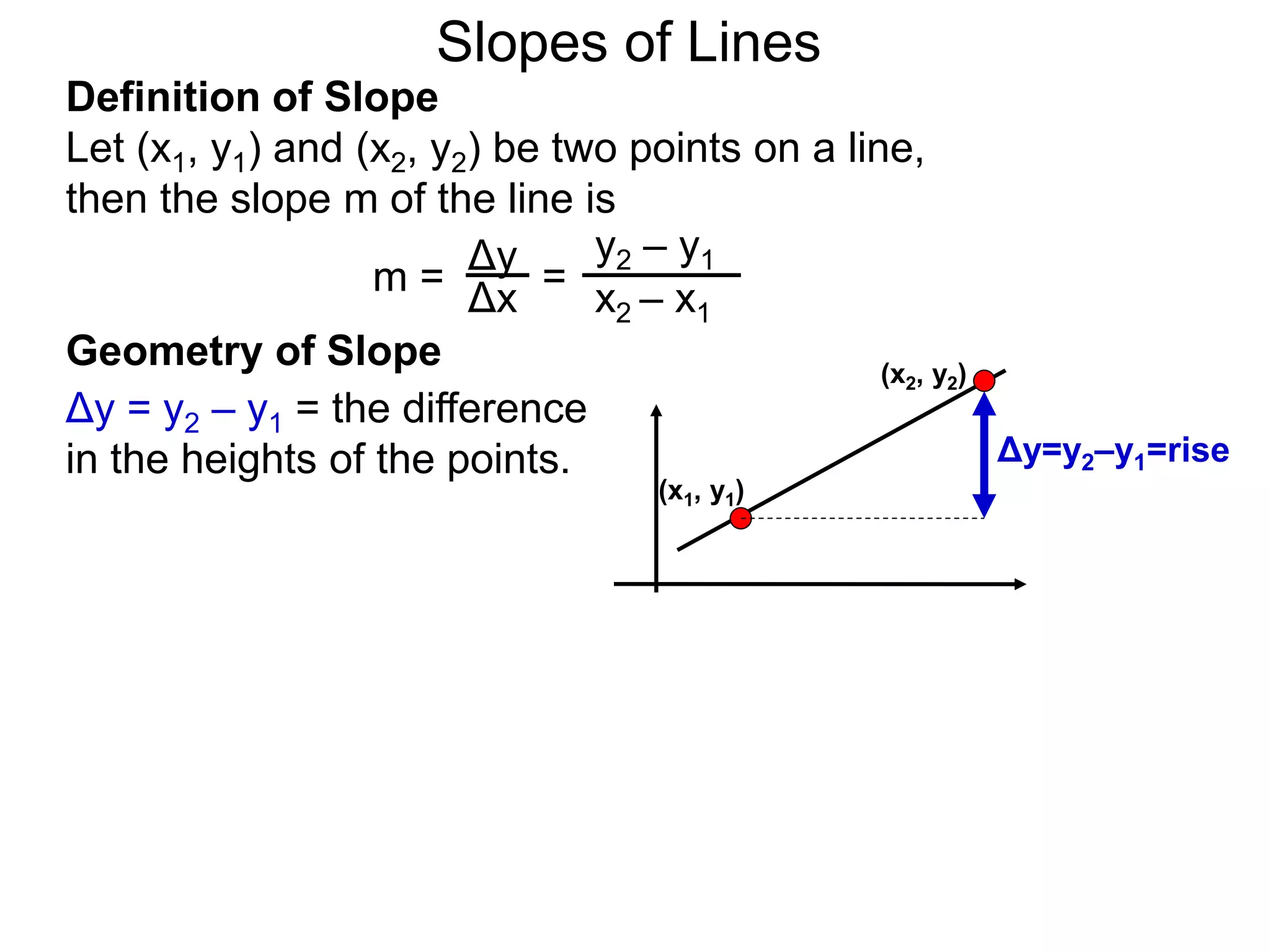
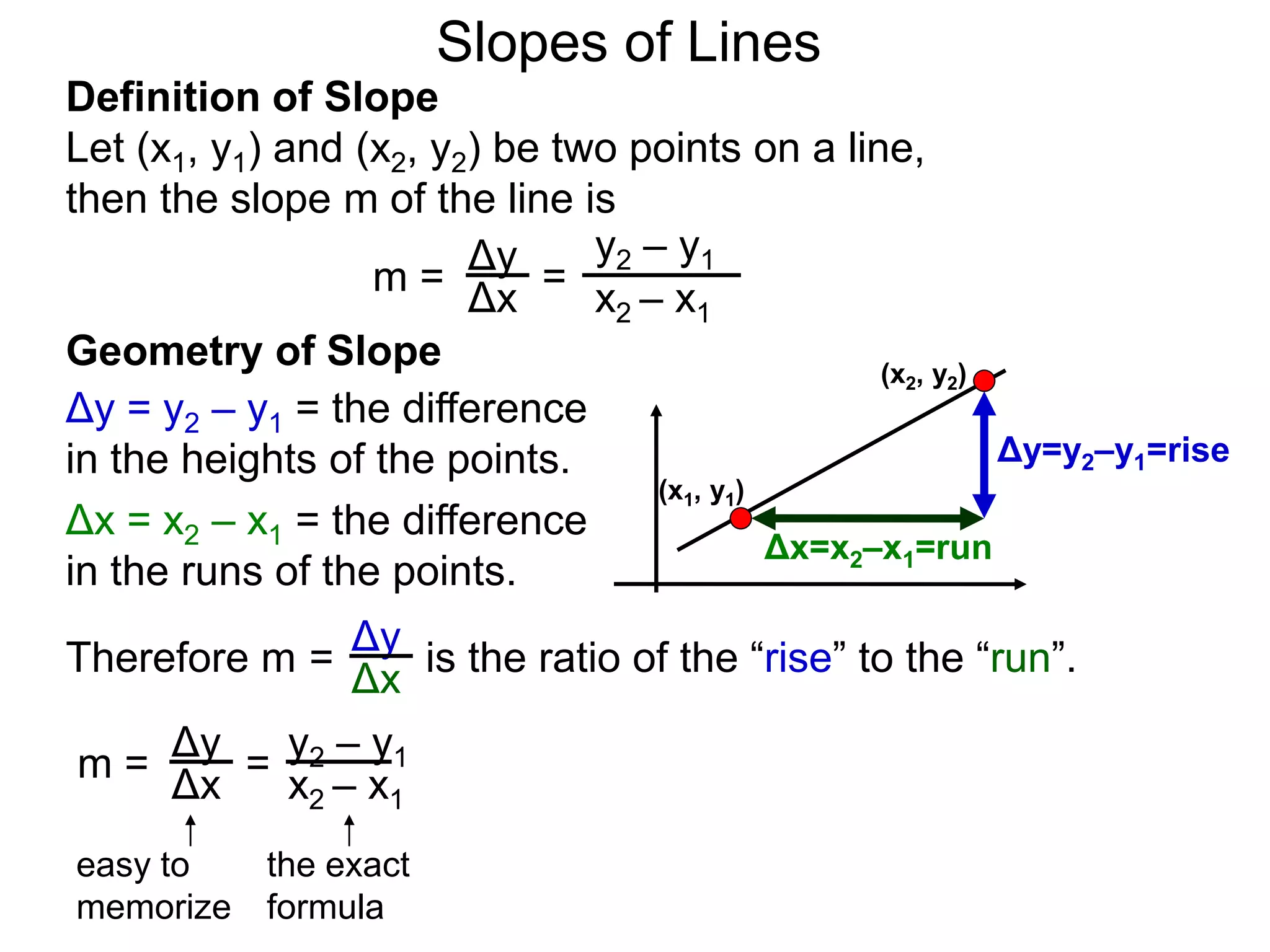
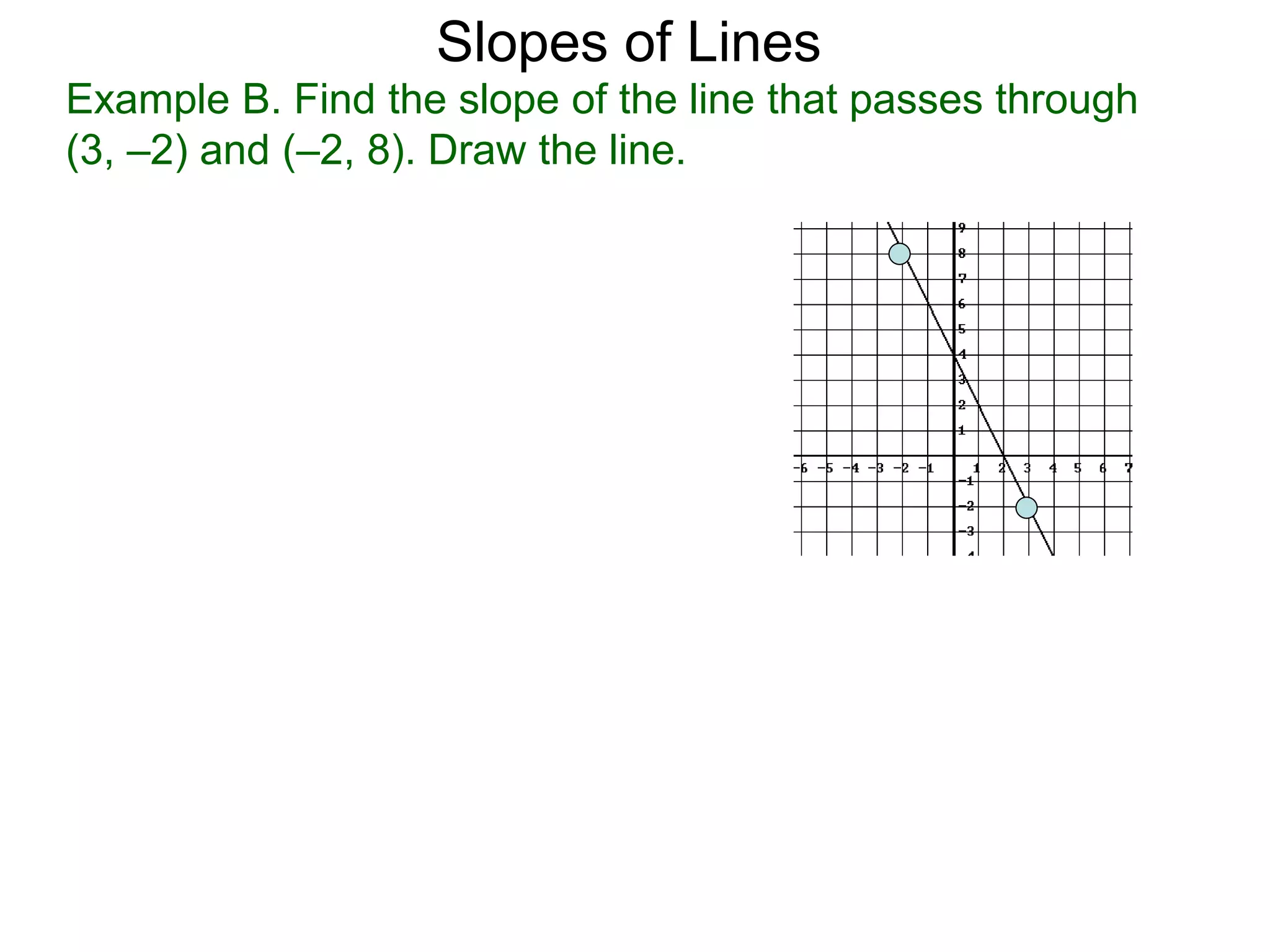
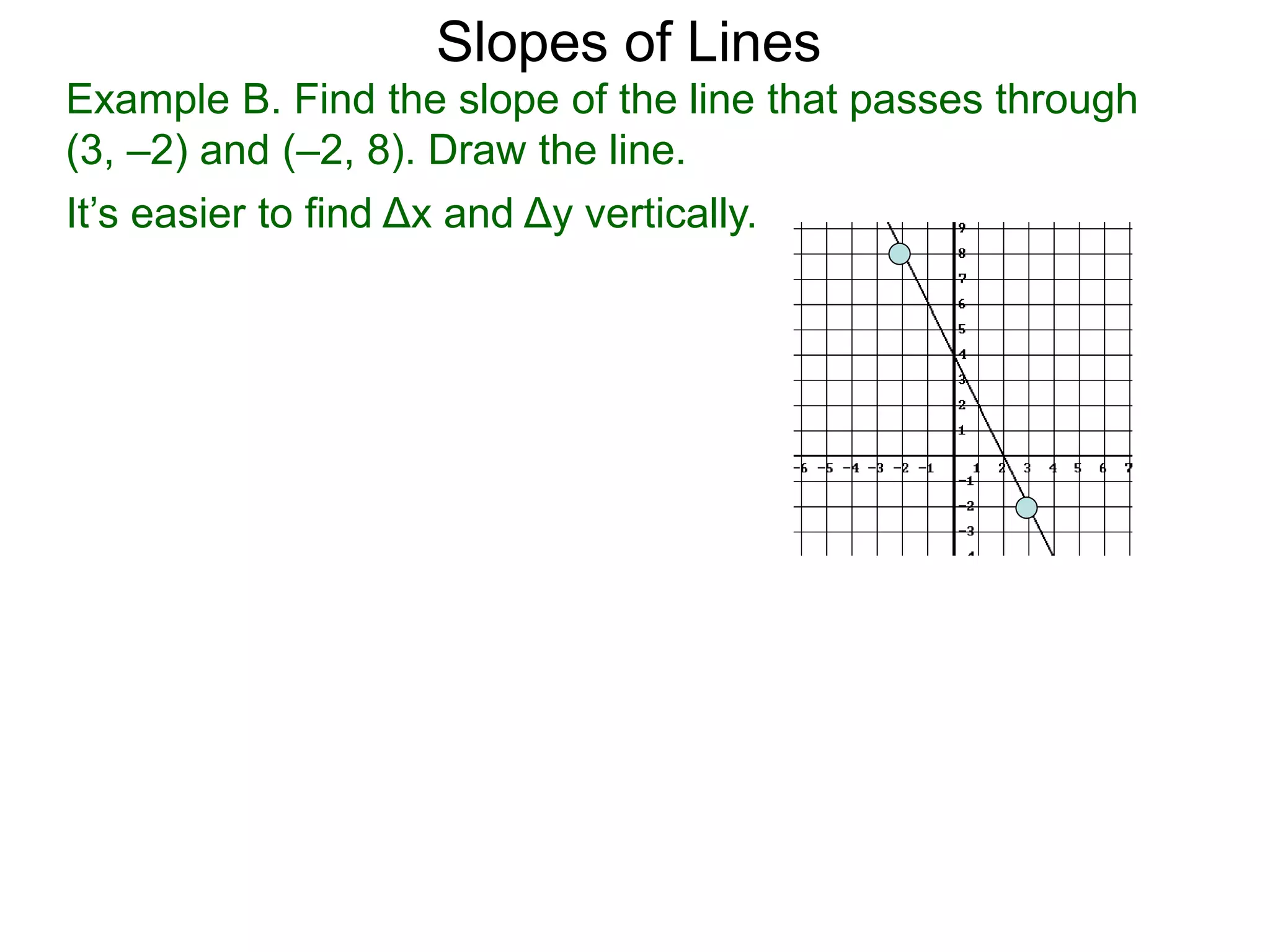
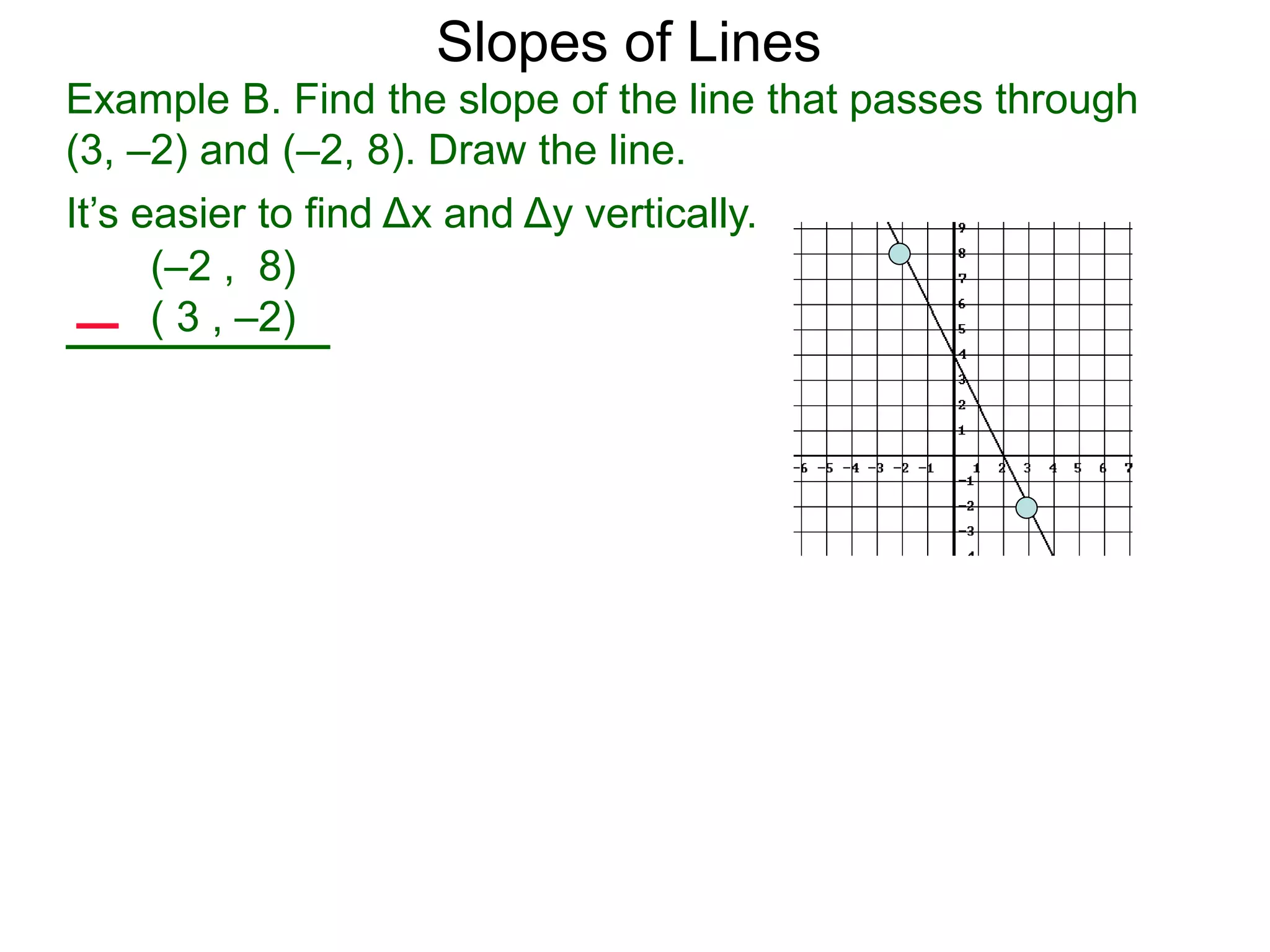
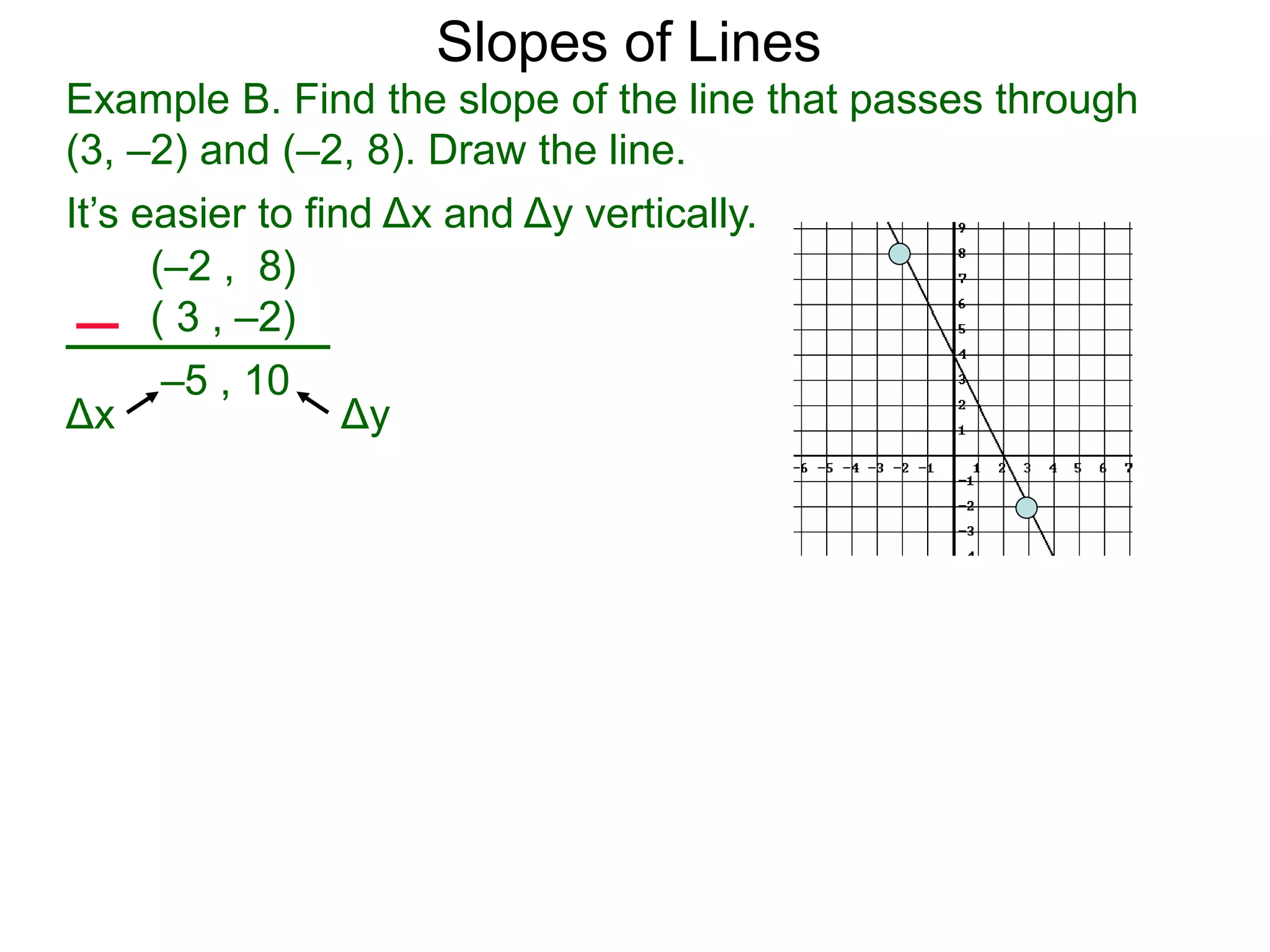
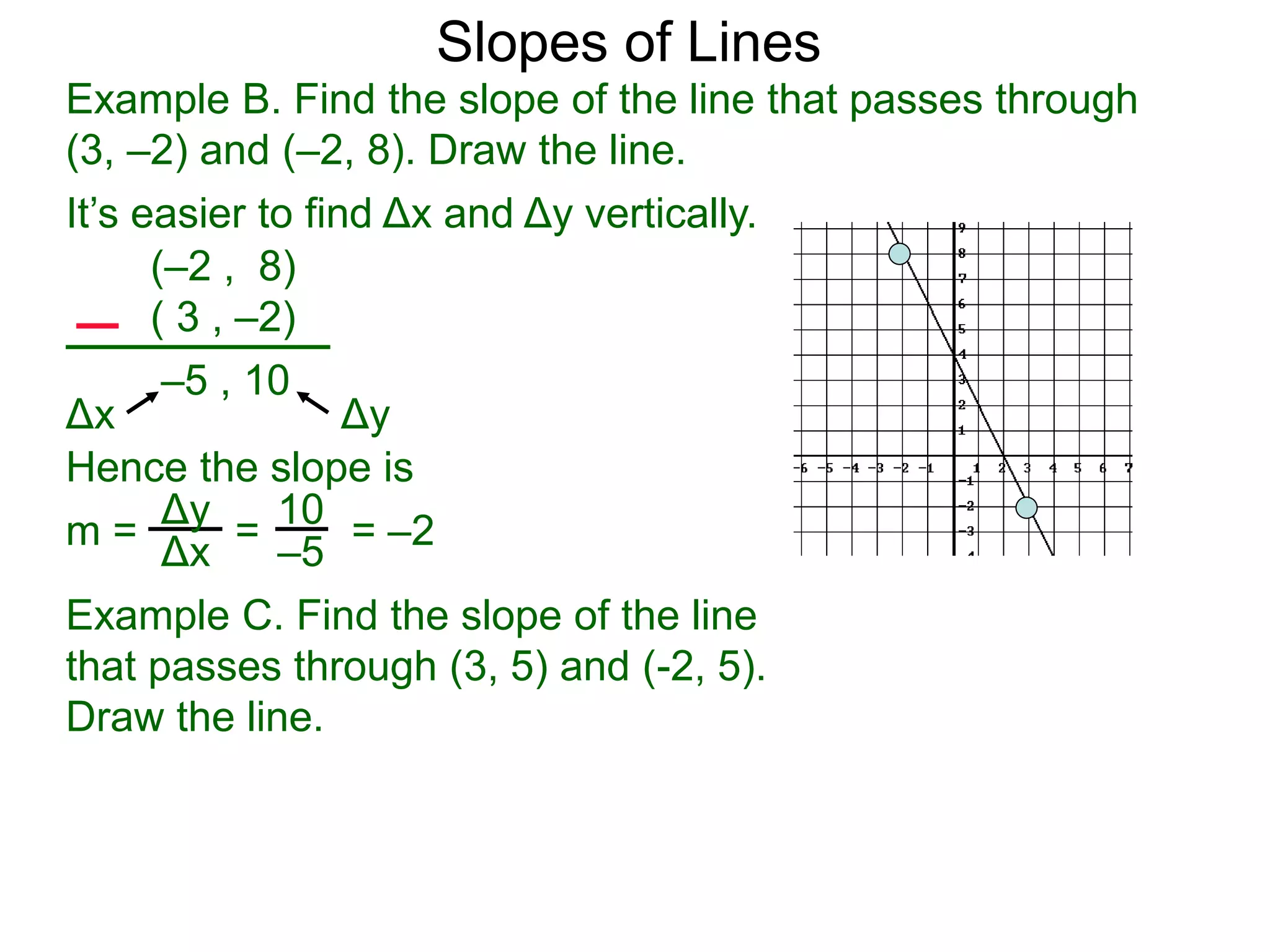
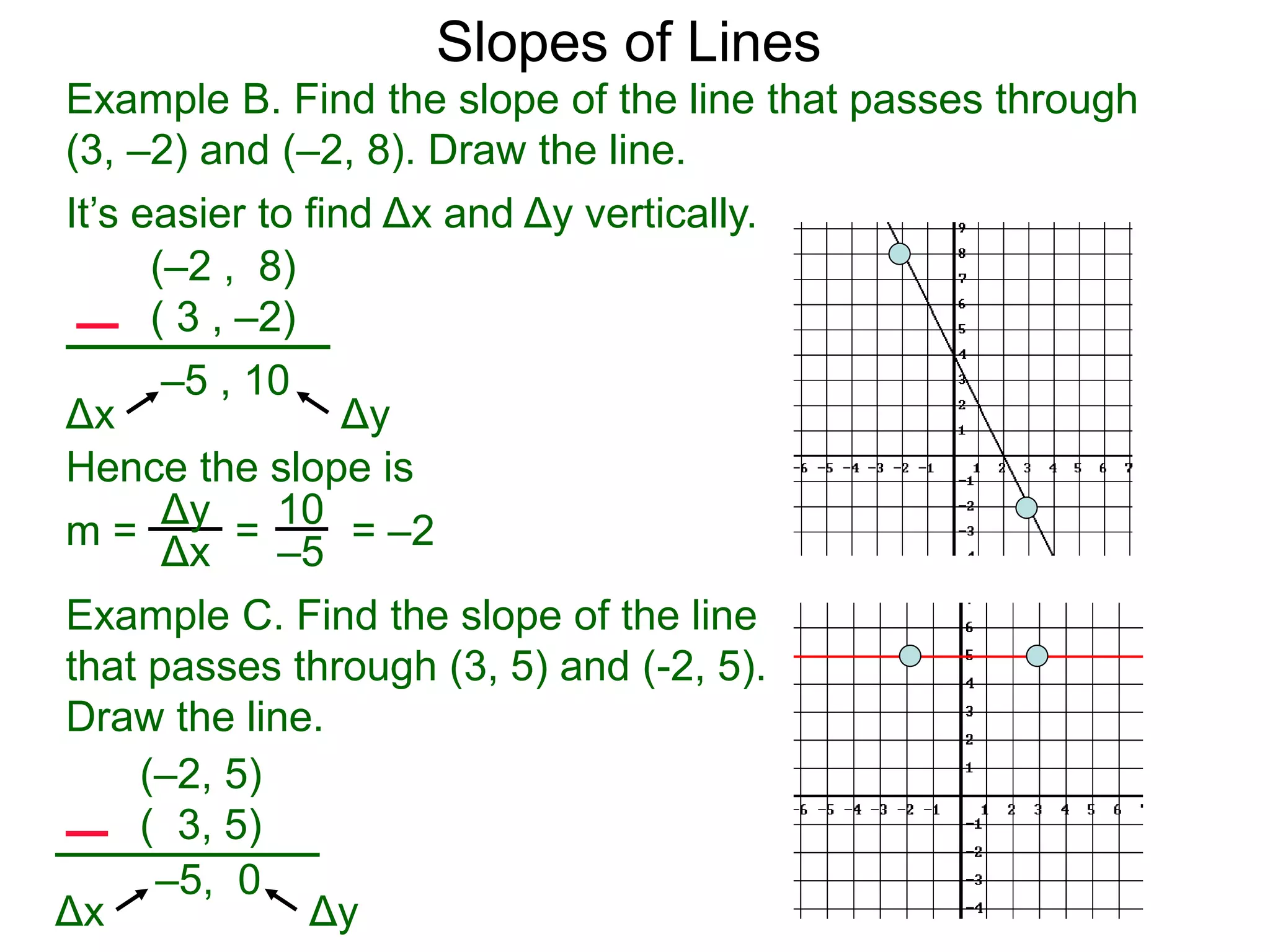
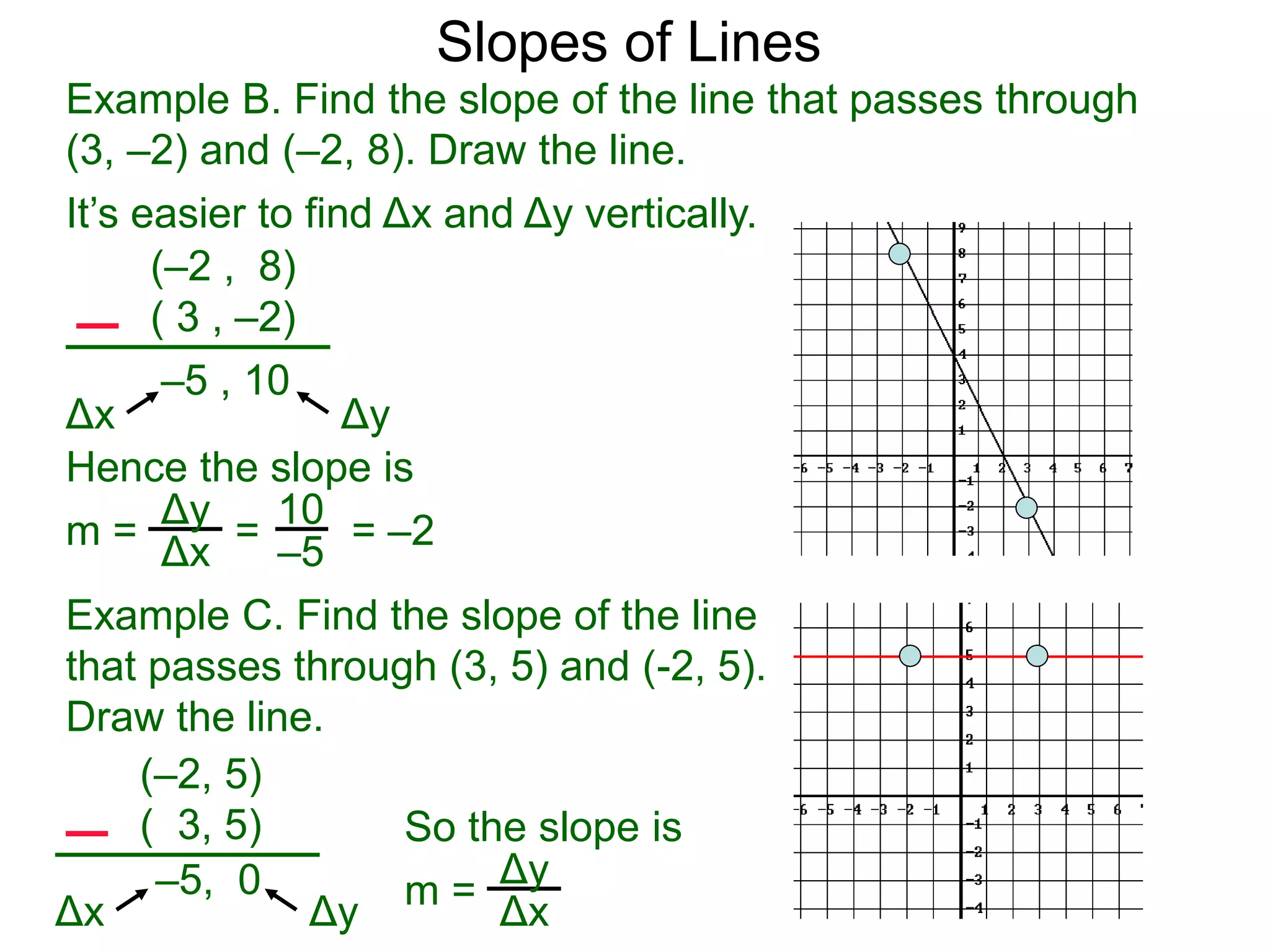
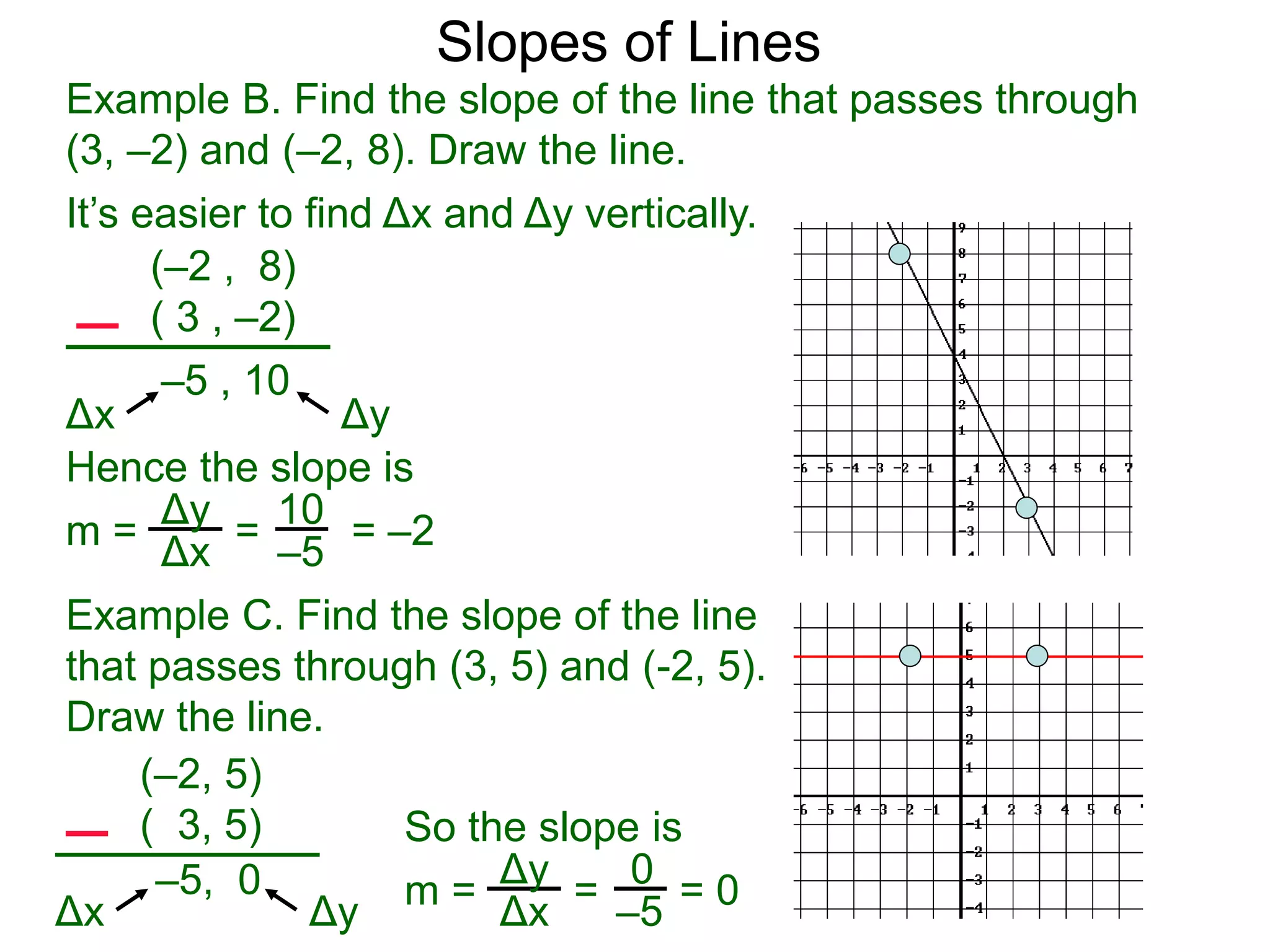
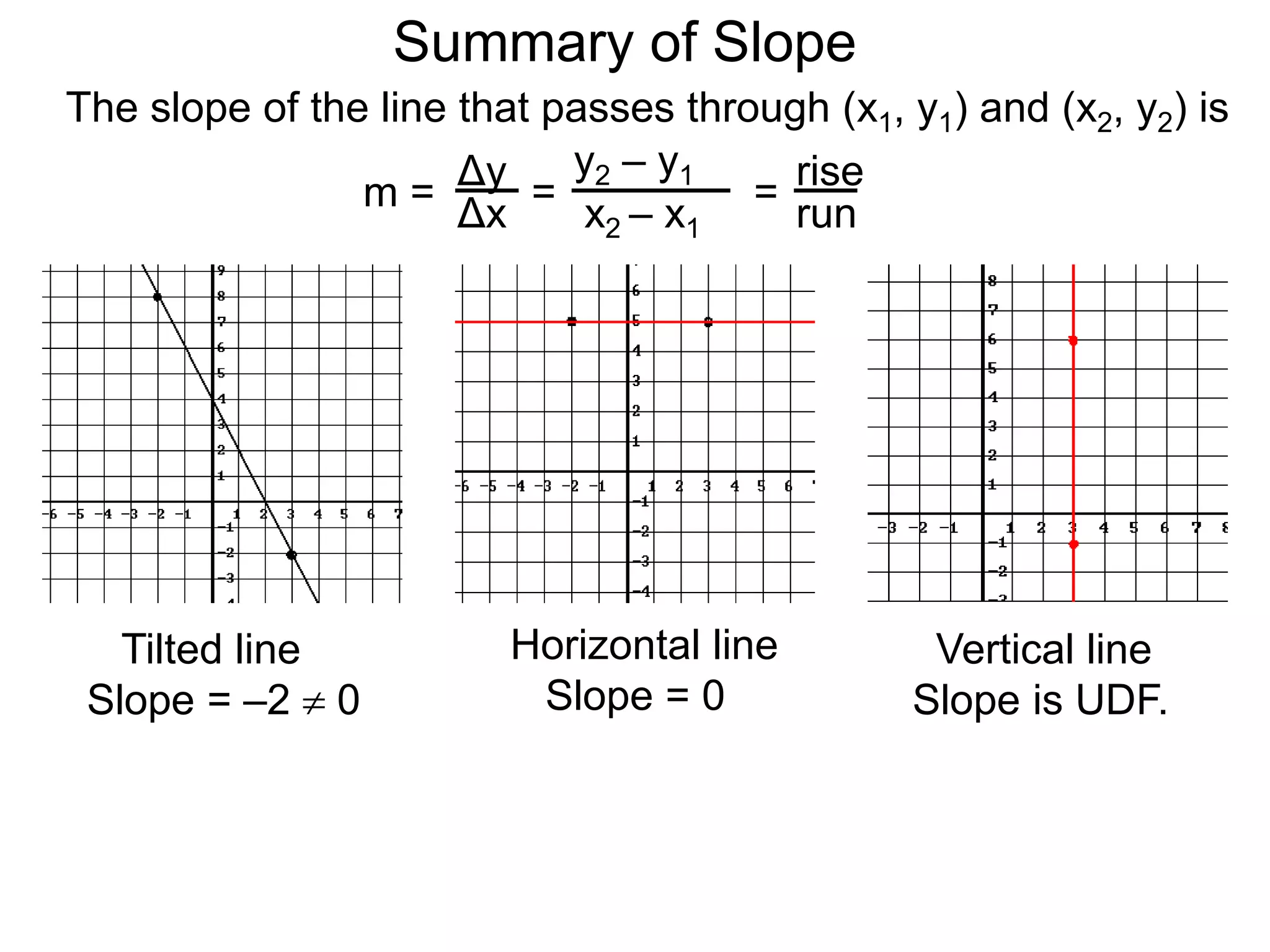
The document discusses slopes and how they are measured and calculated. It defines slope as the ratio of the rise over the run between two points on a line. The slope of a line can be calculated using the formula: m = (y2-y1)/(x2-x1). This measures the steepness of the line. Examples are given to demonstrate calculating the slope between two points and interpreting it geometrically as the ratio of rise over run. Slopes apply to lines, streets, roofs, and any surface with an incline or grade.

1. Slopes of Lines

2. Slopes of Lines
The steepness of a street
is measured in “grade”.

3. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:

4. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:
The 18%-grade means the
ratio of 18 to100 as shown here:
18 ft
100 ft

5. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:
The 18%-grade means the
ratio of 18 to100 as shown here:
18 ft
100 ft
The steepness of a roof is
measured in “pitch”.

6. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:
The 18%-grade means the
ratio of 18 to100 as shown here:
18 ft
100 ft
The steepness of a roof is
measured in “pitch”.
For example:
(12”)

7. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:
The 18%-grade means the
ratio of 18 to100 as shown here:
18 ft
100 ft
Here is outline of a roof with
a pitch of 4:12 or 1/3.
(12”)
The steepness of a roof is
measured in “pitch”.
For example:

8. Slopes of Lines
a Seattle trolleybus climbing
an 18%-grade street (Wikipedia)
The steepness of a street
is measured in “grade”.
For example:
The 18%-grade means the
ratio of 18 to100 as shown here:
18 ft
100 ft
Here is outline of a roof with
a pitch of 4:12 or 1/3.
(12”)
The steepness of a roof is
measured in “pitch”.
For example:
In mathematics, these measurements are called “slopes”.

9. Slopes of Lines
The slope of a line is a number.

10. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.

11. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

12. Slopes of Lines
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value
Definition of Slope

13. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

14. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

15. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

16. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

17. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

18. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

19. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
then Δ x = x2 – x1
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

20. Slopes of Lines
Definition of Slope
Notation: The Greek capital letter Δ (delta) in general
means “the difference” in mathematics.
Δy means the difference in the values of y’s, Δx means the
difference the values of x’s.
Example A. Let y1 = –2, y2 = 5,
then Δy = y2 – y1 = 5 – (–2) = 7
Let x1 = 7, x2 = –4,
then Δ x = x2 – x1 = –4 – 7 = –11
The slope of a line is a number. The slope of a line
measures the amount of tilt, (inclination, steepness) of the
line against the x-axis.
Steep lines have slopes with large absolute value.
Gradual lines have slopes with small absolute value

21. Definition of Slope
Slopes of Lines

22. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
Slopes of Lines
(x1, y1)
(x2, y2)

23. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δxm =
Slopes of Lines
(x1, y1)
(x2, y2)

24. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)

25. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
Geometry of Slope
(x1, y1)
(x2, y2)

26. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.

27. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.

28. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.

29. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m = Δy
Δx
easy to
memorize

30. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m = Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula

31. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run
=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m = Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula
the geometric
meaning

32. Definition of Slope
Let (x1, y1) and (x2, y2) be two points on a line,
then the slope m of the line is
Δy
Δx
y2 – y1
x2 – x1
m = =
rise
run
=
Slopes of Lines
(x1, y1)
(x2, y2)
Δy=y2–y1=rise
Δx=x2–x1=run
Geometry of Slope
Δy = y2 – y1 = the difference
in the heights of the points.
Δx = x2 – x1 = the difference
in the runs of the points.
Δy
Δx
=Therefore m is the ratio of the “rise” to the “run”.
m = Δy
Δx
y2 – y1
x2 – x1
=
easy to
memorize
the exact
formula
the geometric
meaning
Note that
y2 – y1
x2 – x1
y1 – y2
x1 – x2
=
so the numbering of the
two points is not relevant–
we get the same answer.

33. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines

34. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines

35. Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

36. (–2 , 8)
( 3 , –2)
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

37. (–2 , 8)
( 3 , –2)
–5 , 10
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

38. Δy
(–2 , 8)
( 3 , –2)
–5 , 10
Δx
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.

39. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m =

40. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2

41. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.

42. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.

43. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
(–2, 5)
( 3, 5)

44. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx

45. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx
So the slope is
Δx
Δy
m =

46. Δy
Δx
(–2 , 8)
( 3 , –2)
–5 , 10
Δy
Δx
Hence the slope is
10
–5
Example B. Find the slope of the line that passes through
(3, –2) and (–2, 8). Draw the line.
Slopes of Lines
It’s easier to find Δx and Δy vertically.
m = = = –2
Example C. Find the slope of the line
that passes through (3, 5) and (-2, 5).
Draw the line.
Δy
(–2, 5)
( 3, 5)
–5, 0
Δx
So the slope is
Δx
Δy 0
–5m = = = 0

47. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines

48. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.

49. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.

50. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx

51. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =

52. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!

53. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!
Hence the slope m
of a horizontal line is m = 0.

54. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!
Hence the slope m of a vertical line is undefined (UDF).
of a horizontal line is m = 0.

55. As shown in example C, the slope of a horizontal line is 0,
i.e. it’s “tilt” is 0.
Slopes of Lines
Example D. Find the slope of the line that passes
through (3, 2) and (3, 5). Draw the line.
Δy
(3, 5)
(3, 2)
0, 3
Δx
So the slope
Δx
Δy 3
0
m = =
is undefined!
Hence the slope m of a vertical line is undefined (UDF).
of a horizontal line is m = 0.
of a tilted line is a non–zero number.

56. Exercise A. Identify the vertical and the horizontal lines by
inspection first. Find their slopes or if it’s undefined, state so.
Fine the slopes of the other ones by solving for the y.
1. x – y = 3 2. 2x = 6 3. –y – 7= 0
4. 0 = 8 – 2x 5. y = –x + 4 6. 2x/3 – 3 = 6/5
7. 2x = 6 – 2y 8. 4y/5 – 12 = 3x/4 9. 2x + 3y = 3
10. –6 = 3x – 2y 11. 3x + 2 = 4y + 3x 12. 5x/4 + 2y/3 = 2
Exercise B.
13–18. Select two points and estimate the slope of each line.
13. 14. 15.
More on Slopes

57. 16. 17. 18.
Exercise C. Draw and find the slope of the line that passes
through the given two points. Identify the vertical line and the
horizontal lines by inspection first.
19. (0, –1), (–2, 1) 20. (1, –2), (–2, 0) 21. (1, –2), (–2, –1)
22. (3, –1), (3, 1) 23. (1, –2), (–2, 3) 24. (2, –1), (3, –1)
25. (4, –2), (–3, 1) 26. (4, –2), (4, 0) 27. (7, –2), (–2, –6)
28. (3/2, –1), (3/2, 1) 29. (3/2, –1), (1, –3/2)
30. (–5/2, –1/2), (1/2, 1) 31. (3/2, 1/3), (1/3, 1/3)
32. (–2/3, –1/4), (1/2, 2/3) 33. (3/4, –1/3), (1/3, 3/2)
More on Slopes

58. Exercise D.
34. Identify which lines are parallel and which one are
perpendicular.
A. The line that passes through (0, 1), (1, –2)
D. 2x – 4y = 1
B. C.
E. The line that’s perpendicular to 3y = x
F. The line with the x–intercept at 3 and y intercept at 6.
Find the slope, if possible of each of the following lines.
35. The line passes with the x intercept at x = 2,
and y–intercept at y = –5.
More on Slopes

59. 36. The equation of the line is 3x = –5y+7
37. The equation of the line is 0 = –5y+7
38. The equation of the line is 3x = 7
39. The line is parallel to 2y = 5 – 6x
40. the line is perpendicular to 2y = 5 – 6x
41. The line is parallel to the line in problem 30.
42. the line is perpendicular to line in problem 31.
43. The line is parallel to the line in problem 33.
44. the line is perpendicular to line in problem 34.
More on Slopes
Find the slope, if possible of each of the following lines

60. Summary of Slope
The slope of the line that passes through (x1, y1) and (x2, y2) is
Horizontal line
Slope = 0
Vertical line
Slope is UDF.
Tilted line
Slope = –2  0
rise
run
=m =
Δy
Δx
y2 – y1
x2 – x1
=

61. Exercise A.
Select two points and estimate the slope of each line.
1. 2. 3. 4.
Slopes of Lines
5. 6. 7. 8.

62. Exercise B. Draw and find the slope of the line that passes
through the given two points. Identify the vertical line and the
horizontal lines by inspection first.
9. (0, –1), (–2, 1) 10. (1, –2), (–2, 0) 11. (1, –2), (–2, –1)
12. (3, –1), (3, 1) 13. (1, –2), (–2, 3) 14. (2, –1), (3, –1)
15. (4, –2), (–3, 1) 16. (4, –2), (4, 0) 17. (7, –2), (–2, –6)
18. (3/2, –1), (3/2, 1) 19. (3/2, –1), (1, –3/2)
20. (–5/2, –1/2), (1/2, 1) 21. (3/2, 1/3), (1/3, 1/3)
22. (–2/3, –1/4), (1/2, 2/3) 23. (3/4, –1/3), (1/3, 3/2)
Slopes of Lines