The document discusses the Mac-poly Remainder Theorem, which provides a formula for the difference between a function value f(b) and its nth Mac-poly polynomial value pn(b). Specifically: - The theorem states that for a function f(x) that is infinitely differentiable over an interval containing [0,b], there exists a c between b and 0 such that f(b) = pn(b) + Rn(b), where Rn(b) is the remainder term involving the (n+1)th derivative of f. 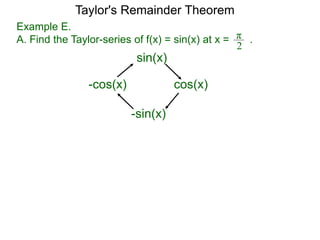- An example shows applying the theorem to the function f(x)=ex, finding the Mac-poly is the series 1 + x +

1. Mac-poly Remainder Theorem
Let P(x) be the Mac series of f(x), an infinitely
differentiable function.

2. Mac-poly Remainder Theorem
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x).

3. Mac-poly Remainder Theorem
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example.

4. Mac-poly Remainder Theorem
Example A.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example.

5. Mac-poly Remainder Theorem
Example A.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example. y = f(x)

6. Mac-poly Remainder Theorem
Example A.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
We leave it as an exercise that its derivatives of all
the orders are 0, i.e. f(n)(0) = 0 for all n.
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example. y = f(x)

7. Mac-poly Remainder Theorem
Example A.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
We leave it as an exercise that its derivatives of all
the orders are 0, i.e. f(n)(0) = 0 for all n.
Therefore its Maclaurin series P(x) = 0.
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example. y = f(x)

8. Mac-poly Remainder Theorem
Example A.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
We leave it as an exercise that its derivatives of all
the orders are 0, i.e. f(n)(0) = 0 for all n.
Therefore its Maclaurin series P(x) = 0.
Clearly P(x) is not the same as f(x).
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example. y = f(x)

9. Mac-poly Remainder Theorem
Example A.
In the following discussion, we will assume that all
the functions are infinitely differentiable over an open
interval unless otherwise stated.
Let P(x) be the Mac series of f(x), an infinitely
differentiable function at x = 0. It would be nice if for
every x that P(x) = f(x). However, such is not the case
by the following example.
Let f(x) = {e-1/x2
if x = 0
0 if x = 0
We leave it as an exercise that its derivatives of all
the orders are 0, i.e. f(n)(0) = 0 for all n.
Therefore its Maclaurin series P(x) = 0.
Clearly P(x) is not the same as f(x).
y = f(x)

10. Mac-poly Remainder Theorem
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).

11. Mac-poly Remainder Theorem
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).
We will give the theorem where pn is the Maclaurin
polynomial first (i.e. expanded about 0).

12. Mac-poly Remainder Theorem
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).
We will give the theorem where pn is the Maclaurin
polynomial first (i.e. expanded about 0).
Mac-poly Remainder Theorem: Let f(x) be an infinitely
differentiable function over an open interval that
contains [0, b] and pn(x) be its n'th Mac-poly,

13. Mac-poly Remainder Theorem
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).
We will give the theorem where pn is the Maclaurin
polynomial first (i.e. expanded about 0).
0
( )[ ]
b
f(x) is infinitely differentiable in here
Mac-poly Remainder Theorem: Let f(x) be an infinitely
differentiable function over an open interval that
contains [0, b] and pn(x) be its n'th Mac-poly,

14. Mac-poly Remainder Theorem
Mac-poly Remainder Theorem: Let f(x) be an infinitely
differentiable function over an open interval that
contains [0, b] and pn(x) be its n'th Mac-poly,
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).
then there exists a "c" between b and 0
We will give the theorem where pn is the Maclaurin
polynomial first (i.e. expanded about 0).
0
( )[ ]
bc
f(x) is infinitely differentiable in here

15. Mac-poly Remainder Theorem
Mac-poly Remainder Theorem: Let f(x) be an infinitely
differentiable function over an open interval that
contains [0, b] and pn(x) be its n'th Mac-poly,
Taylor's Remainder Theorem gives a formula for
the difference between the function value f(b) and
pn(b) where pn is the n'th Taylor/Mac polynomial
(expanded about some point a / 0).
then there exists a "c" between b and 0 such that
f(b) = pn(b) +
We will give the theorem where pn is the Maclaurin
polynomial first (i.e. expanded about 0).
bn+1
(n + 1)!
f(n+1)(c)
0
( )[ ]
bc
f(x) is infinitely differentiable in here

16. Mac-poly Remainder Theorem
or in full detail,
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+

17. Mac-poly Remainder Theorem
or in full detail,
The difference term denoted as Rn(b)bn+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder
(or error) term (there are other forms).
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+

18. Mac-poly Remainder Theorem
or in full detail,
The difference term denoted as Rn(b)bn+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder
(or error) term (there are other forms).
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+
Remarks:

19. Mac-poly Remainder Theorem
or in full detail,
The difference term denoted as Rn(b)bn+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder
(or error) term (there are other forms).
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+
Remarks:
* the theorem also works for the interval [b, 0]

20. Mac-poly Remainder Theorem
or in full detail,
The difference term denoted as Rn(b)bn+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder
(or error) term (there are other forms).
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+
Remarks:
* the theorem also works for the interval [b, 0]
* the value c changes if the value of b or n changes

21. Mac-poly Remainder Theorem
or in full detail,
The difference term denoted as Rn(b)bn+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder
(or error) term (there are other forms).
f '(0)b f(2)(0)
+ 2!= f(0) + b2f(b) +.. f(n)(0)
n! bn+ bn+1
(n + 1)!
f(n+1)(c)
+
Remarks:
* the theorem also works for the interval [b, 0]
* the value c can't be easily determined, we just know
there is at least one c that fits the description
* the value c changes if the value of b or n changes

22. Mac-poly Remainder Theorem
Example B. f(x) = ex is infinitely differentiable everywhere.

23. Pn(x) = Σk=0
xk
k!
n
= 1 + x + x2
2!
+ .. + xn
n!
Mac-poly Remainder Theorem
Example B. f(x) = ex is infinitely differentiable everywhere.
The Mac-poly of ex is

24. The Mac-poly of ex is
Pn(x) = Σk=0
xk
k!
n
= 1 + x + x2
2!
+ .. + xn
n!
At x = b, by the theorem we have
f(b) = eb = 1 + b +
b2
2! + .. +
bn
n!
+
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Mac-poly Remainder Theorem
Example B. f(x) = ex is infinitely differentiable everywhere.

25. Pn(x) = Σk=0
xk
k!
n
= 1 + x + x2
2!
+ .. + xn
n!
At x = b, by the theorem we have
f(b) = eb = 1 + b +
b2
2! + .. +
bn
n!
+
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since f(n+1)(x) = ex so f(n+1)(c) = ec. Hence
f(b) = eb = 1 + b +
b2
2!
+ .. +
bn
n!
+
ec
(n+1)!
bn+1
for some c that is between 0 and b.
Mac-poly Remainder Theorem
Hence
Example B. f(x) = ex is infinitely differentiable everywhere.
The Mac-poly of ex is

26. Example B. f(x) = ex is infinitely differentiable everywhere.
Pn(x) = Σk=0
xk
k!
n
= 1 + x + x2
2!
+ .. + xn
n!
At x = b, by the theorem we have
f(b) = eb = 1 + b +
b2
2! + .. +
bn
n!
+
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since f(n+1)(x) = ex so f(n+1)(c) = ec. Hence
f(b) = eb = 1 + b +
b2
2!
+ .. +
bn
n!
+
ec
(n+1)!
bn+1
for some c that is between 0 and b.
Mac-poly Remainder Theorem
Hence
The point here is not to find c but to use the formula to
calculate the behavior of the error as n  .∞
The Mac-poly of ex is

27. Example C. Show that in the above example, the remainder
term goes to 0 as n  ∞.
Mac-poly Remainder Theorem

28. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
∞.
Mac-poly Remainder Theorem

29. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
∞.
Mac-poly Remainder Theorem
We have that

30. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
∞.
The maximum possible value of ec is eb.
Mac-poly Remainder Theorem
We have that

31. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
∞.
The maximum possible value of ec is eb. Write eb as K.
Mac-poly Remainder Theorem
We have that

32. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
∞.
The maximum possible value of ec is eb. Write eb as K.
ec
(n+1)!
bn+1
< bn+1
(n+1)!
KHence
Mac-poly Remainder Theorem
We have that

33. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
As n  we've that K∞,
∞.
The maximum possible value of ec is eb. Write eb as K.
ec
(n+1)!
bn+1
< bn+1
(n+1)!
K
bn+1
(n+1)!
 0
Hence
Mac-poly Remainder Theorem
We have that

34. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
As n  we've that K∞,
∞.
The maximum possible value of ec is eb. Write eb as K.
ec
(n+1)!
bn+1
< bn+1
(n+1)!
K
bn+1
(n+1)!
 0 (e.g. use ratio test).
Hence
Mac-poly Remainder Theorem
We have that

35. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
As n  we've that K∞,
∞.
The maximum possible value of ec is eb. Write eb as K.
ec
(n+1)!
bn+1
< bn+1
(n+1)!
K
bn+1
(n+1)!
 0 (e.g. use ratio test).
Hence the error term
ec
(n+1)!
bn+1
 0 as n 
Hence
∞.
Mac-poly Remainder Theorem
We have that

36. Example C. Show that in the above example, the remainder
term goes to 0 as n  Hence f(b) = P(b) for all values b
where P(x) is the Mac-series.
f(b) = eb = 1 + b + b2
2!
+ .. + bn
n!
+
ec
(n+1)!
bn+1
where b is a fixed value and c is between 0 and b.
As n  we've that K∞,
∞.
The maximum possible value of ec is eb. Write eb as K.
ec
(n+1)!
bn+1
< bn+1
(n+1)!
K
bn+1
(n+1)!
 0 (e.g. use ratio test).
Hence the error term
ec
(n+1)!
bn+1
 0 as n 
Hence
∞.
This means the f(b) = Σn=0
bn
n!
∞
= P(b).
Mac-poly Remainder Theorem
We have that

37. Mac-poly Remainder Theorem
We state the following theorem.

38. Mac-poly Remainder Theorem
We state the following theorem.
Theorem: Given f(x), and [0, b] as in the Mac-poly
Remainder theorem. Let P(x) be the Mac-series of
f(x), then f(b) = P(b) if and only if the error term
Rn(b) = bn+1
(n + 1)!
f(n+1)(c)
 0 as n  ∞.

39. Mac-poly Remainder Theorem
We state the following theorem.
(reminder: c is not fixed, it changes as n changes.)
Theorem: Given f(x), and [0, b] as in the Mac-poly
Remainder theorem. Let P(x) be the Mac-series of
f(x), then f(b) = P(b) if and only if the error term
Rn(b) = bn+1
(n + 1)!
f(n+1)(c)
 0 as n  ∞.

40. Mac-poly Remainder Theorem
We state the following theorem.
(reminder: c is not fixed, it changes as n changes.)
Theorem: Given f(x), and [0, b] as in the Mac-poly
Remainder theorem. Let P(x) be the Mac-series of
f(x), then f(b) = P(b) if and only if the error term
Rn(b) = bn+1
(n + 1)!
f(n+1)(c)
 0 as n  ∞.
A function that is equal to its Mac-series over an
open interval around 0 is said to be analytic at 0.

41. Mac-poly Remainder Theorem
We state the following theorem.
(reminder: c is not fixed, it changes as n changes.)
Theorem: Given f(x), and [0, b] as in the Mac-poly
Remainder theorem. Let P(x) be the Mac-series of
f(x), then f(b) = P(b) if and only if the error term
Rn(b) = bn+1
(n + 1)!
f(n+1)(c)
 0 as n  ∞.
A function that is equal to its Mac-series over an
open interval around 0 is said to be analytic at 0.
The function f(x) = ex is analytic at 0.

42. Mac-poly Remainder Theorem
We state the following theorem.
(reminder: c is not fixed, it changes as n changes.)
Theorem: Given f(x), and [0, b] as in the Mac-poly
Remainder theorem. Let P(x) be the Mac-series of
f(x), then f(b) = P(b) if and only if the error term
Rn(b) = bn+1
(n + 1)!
f(n+1)(c)
 0 as n  ∞.
A function that is equal to its Mac-series over an
open interval around 0 is said to be analytic at 0.
The function f(x) = ex is analytic at 0.
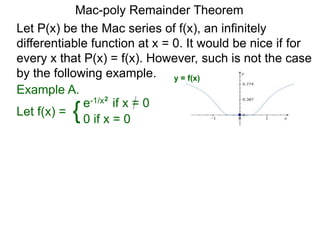
The function
f(x) = {e-1/x2
if x = 0
0 if x = 0
is infinitely differentiable but not analytic at 0.

43. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
Mac-poly Remainder Theorem
∞

44. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
∞

45. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
At x = b, the remainder is Rn(b) =
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
∞

46. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
At x = b, the remainder is Rn(b) =
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since the higher derivatives of cos(x) are ±sin(x), or ±cos(x),
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
∞

47. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
At x = b, the remainder is Rn(b) =
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since the higher derivatives of cos(x) are ±sin(x), or ±cos(x),
we may assume that |f(n+1)(c)| ≤ 1.
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
∞

48. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
At x = b, the remainder is Rn(b) =
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since the higher derivatives of cos(x) are ±sin(x), or ±cos(x),
we may assume that |f(n+1)(c)| ≤ 1.
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
f(n+1)(c)
(n+1)!
bn+1 <
(n+1)!
bn+1
 0 as n  ∞.Hence,
∞

49. Example D. Let f(x) = cos(x). Show that the Lagrange form
of the error Rn(b) of it's Mac-poly goes to 0 as n  and
conclude from that f(x) is the same as it's Mac-series.
P(x) =
At x = b, the remainder is Rn(b) =
f(n+1)(c)
(n+1)!
for some c that is between 0 and b.
bn+1
Since the higher derivatives of cos(x) are ±sin(x), or ±cos(x),
we may assume that |f(n+1)(c)| ≤ 1.
Mac-poly Remainder Theorem
+
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
..
The Mac-series is
f(n+1)(c)
(n+1)!
bn+1 <
(n+1)!
bn+1
 0 as n  ∞.
Therefore f(x) = P(x) = +
4!
x4
6!
x6
8!
x8
+1 – –
2!
x2
.. for all x.
∞
Hence,

50. Taylor's Remainder Theorem

51. Taylor's Remainder Theorem
We state the general form of the Taylor's remainder
formula.

52. Taylor's Remainder Theorem
We state the general form of the Taylor's remainder
formula.
Taylor's Remainder Theorem (General Form):
Let f(x) be an infinitely differentiable function over
some open interval that contains [a, b]

53. Taylor's Remainder Theorem
We state the general form of the Taylor's remainder
formula.
Taylor's Remainder Theorem (General Form):
Let f(x) be an infinitely differentiable function over
some open interval that contains [a, b]
a
( )[ ]
b
f(x) is infinitely differentiable in here

54. Taylor's Remainder Theorem
We state the general form of the Taylor's remainder
formula.
Taylor's Remainder Theorem (General Form):
Let f(x) be an infinitely differentiable function over
some open interval that contains [a, b] and
pn(x) =
be the n'th Taylor-poly expanded at a.
a
( )[ ]
b
f(x) is infinitely differentiable in here
Σk=0
n
(x – a)k
k!
f(k)(a)

55. Taylor's Remainder Theorem
We state the general form of the Taylor's remainder
formula.
Taylor's Remainder Theorem (General Form):
Let f(x) be an infinitely differentiable function over
some open interval that contains [a, b] and
pn(x) =
be the n'th Taylor-poly expanded at a.
Then there exists a "c" between a and b such that
f(b) = pn(b) + (b – a)n+1
(n + 1)!
f(n+1)(c)
a
( )[ ]
bc
f(x) is infinitely differentiable in here
Σk=0
n
(x – a)k
k!
f(k)(a)

56. or in full detail,
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Taylor's Remainder Theorem
+ Rn(b)

57. or in full detail,
where Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder.
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Taylor's Remainder Theorem
+ Rn(b)

58. or in full detail,
where Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder.
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Again, we note the following
Taylor's Remainder Theorem
+ Rn(b)

59. or in full detail,
where Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder.
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Again, we note the following
* the theorem also works for the interval [b, a]
Taylor's Remainder Theorem
+ Rn(b)

60. or in full detail,
where Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder.
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Again, we note the following
* the theorem also works for the interval [b, a]
* the value c changes if the value of b or n changes
Taylor's Remainder Theorem
+ Rn(b)

61. or in full detail,
where Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
is the Lagrange form of the Taylor-remainder.
f '(a)(b – a)
f(2)(a)
+ 2!= f(a) + (b – a)2
f(b) ..
f(n)(a)
n!
(b – a)n+
Again, we note the following
* the theorem also works for the interval [b, a]
* the value c can't be easily determined, we just know
there is at least one c that fits the description
* the value c changes if the value of b or n changes
Taylor's Remainder Theorem
+ Rn(b)

62. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
Taylor's Remainder Theorem

63. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
Taylor's Remainder Theorem

64. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, …
Taylor's Remainder Theorem

65. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, … So the Taylor expansion is
= 1P(x)
Taylor's Remainder Theorem

66. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, … So the Taylor expansion is
–= 1P(x)
(x – π/2)2
2!
Taylor's Remainder Theorem

67. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, … So the Taylor expansion is
–= 1P(x)
(x – π/2)2
2!
1(x – π/2)4
+
4!
Taylor's Remainder Theorem

68. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, … So the Taylor expansion is
–= 1P(x)
(x – π/2)2
2!
1(x – π/2)4
+
4!
–
1(x – π/2)6
6!
..
1(x – π/2)8
+
8!
Taylor's Remainder Theorem

69. Example E.
A. Find the Taylor-series of f(x) = sin(x) at x = .π
2
sin(x)
cos(x)
-sin(x)
-cos(x)
At x =
π
2 , we get the sequence of coefficients
1, 0, -1, 0, 1, 0, -1, … So the Taylor expansion is
–= 1P(x)
(x – π/2)2
2!
1(x – π/2)4
+
4!
–
1(x – π/2)6
6!
..
or P(x) = Σ
(-1)n(x – π/2)2n
(2n)!n=0
n =∞
1(x – π/2)8
+
8!
Taylor's Remainder Theorem

70. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )π/2
Taylor's Remainder Theorem

71. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
π/2
Taylor's Remainder Theorem

72. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
Taylor's Remainder Theorem

73. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
where f(n+1) may be ±sin(x) or ±cos(x) and for some c that is
between a and b.
Taylor's Remainder Theorem

74. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
where f(n+1) may be ±sin(x) or ±cos(x) and for some c that is
between a and b.
Since |f(n+1)(c)| < 1,
Taylor's Remainder Theorem

75. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
where f(n+1) may be ±sin(x) or ±cos(x) and for some c that is
between a and b.
Since |f(n+1)(c)| < 1, we've (b – )n+1
(n + 1)!
f(n+1)(c) π
2 <
(n + 1)!
(b – )n+1π
2
Taylor's Remainder Theorem

76. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
where f(n+1) may be ±sin(x) or ±cos(x) and for some c that is
between a and b.
Since |f(n+1)(c)| < 1, we've (b – )n+1
(n + 1)!
f(n+1)(c) π
2 <
(n + 1)!
(b – )n+1π
2
Again, as n  we've
(n + 1)!
(b – )n+1π
2  0∞,
Taylor's Remainder Theorem

77. Example E.
B. Describe the Taylor remainder Rn(b) and show that
f(b) = P(b) for all values b. (a = )
The remainder Rn(b) = (b – a)n+1
(n + 1)!
f(n+1)(c)
=
π/2
(b – )n+1
(n + 1)!
f(n+1)(c) π
2
where f(n+1) may be ±sin(x) or ±cos(x) and for some c that is
between a and b.
Since |f(n+1)(c)| < 1, we've (b – )n+1
(n + 1)!
f(n+1)(c) π
2 <
(n + 1)!
(b – )n+1π
2
Again, as n  we've
(n + 1)!
(b – )n+1π
2  0∞,
Hence Rn(b)  0 and so f(b) = P(b) for all b.
Taylor's Remainder Theorem

78. Differentiation and Integration of Power Series
The Taylor series of f(x) is the only power series that
could be the same as f(x).

79. Σk=0
∞
Differentiation and Integration of Power Series
Let f(x) = ck(x – a)k for all x in an open interval
(a – R, a + R) for some R, then the series ck(x – a)k
is the Taylor series P(x) of f(x).
Σk=0
∞
Theorem (Uniqueness theorem for Taylor series) :
The Taylor series of f(x) is the only power series that
could be the same as f(x).